Равномерное распределение
Условные законы распределения, условные числовые характеристики системы случайных величин, условие независимости случайных величин
Корреляция, свойство коэффициента корреляции. Линейная корреляция
Предельные теоремы теории вероятностей. Центральная предельная теорема Ляпунова
Основные категории статистики
Методы первичного анализа экспериментальных данных. Построение вариационных рядов и определение их основных характеристик
Размах вариации R = 210 – 150 = 60 шт
Сформулируйте определения полигона частот, гистограммы и кумуляты
При увеличении объёма выборки оценка должна сходиться по вероятности к истинному значению параметра. В этом случае оценку называют состоятельной
Статистики. Критерии. Критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора
Навигация
Предельные теоремы теории вероятностей. Центральная предельная теорема Ляпунова
Основные понятия статистики
86945
знаков
23
таблицы
25
изображений
3. Предельные теоремы теории вероятностей. Центральная предельная теорема Ляпунова
Как уже говорилось, при достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта.
Предельные теоремы теории вероятностей устанавливают соответствие между теоретическими и экспериментальными характеристиками случайных величин при большом количестве испытаний.
В рассмотренном выше законе больших чисел нечего не говорилось о законе распределения случайных величин. Поставим задачу нахождения предельного закона распределения суммы 
, когда число слагаемых п неограниченно возрастает. Эту задачу решает Центральная предельная теорема Ляпунова.
В зависимости от условий распределения случайных величин Xi, образующих сумму, возможны различные формулировки центральной предельной теоремы. Рассмотрим один из вариантов.
Допустим, что случайные величины Xi взаимно независимы и одинаково распределены.
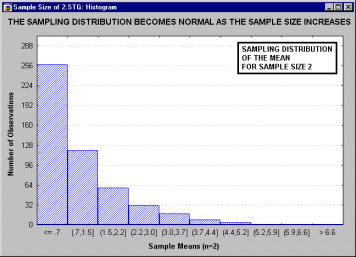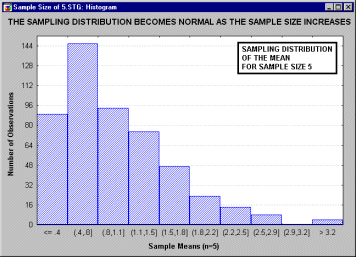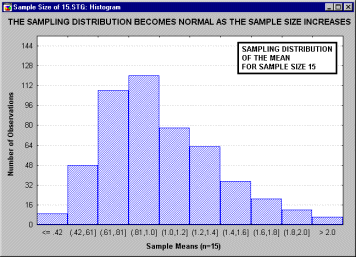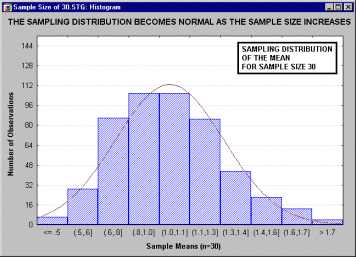
Теорема. Если случайные величины Xi взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием т и дисперсией s2, причем существует третий абсолютный момент n3, то при неограниченном увеличении числа испытаний п закон распределения суммы неограниченно приближается к нормальному.
Контрольные вопросы:
1. Сформулируйте теорему больших чисел Бернулли.
2. Сформулируйте теорему больших чисел Чебышева.
3. Сформулируйте теорему A.M. Ляпунова.
Раздел 2. Математическая статистика
Аннотация
Математическая статистика изучает, как и теория вероятностей, случайные явления, использует одинаковые с ней определения, понятия и методы и основана на той же самой аксиоматике А.Н. Колмогорова. Однако задачи, решаемые математической статистикой , носят специфический характер.
Теория вероятностей исследует явления, заданные полностью их моделью, и выявляет еще до опыта те статистические закономерности, которые будут иметь место после его проведения
В математической статистике вероятностная модель явления определена с точностью до неизвестных параметров. Отсутствие сведений о параметрах компенсируется тем, что позволяется проводить «пробные» испытания и на их основе восстанавливать недостающую информацию
Тема 2.1. Описательная статистика
1. Два основных направления исследований в статистике.2. Основные категории статистики.
3. Методы первичного анализа экспериментальных данных. Построение вариационных рядов и определение их основных характеристик
4. Графическое представление вариационных рядов.
1. Два основных направления исследований в статистикеВ математической статистике принято выделять два направления: параметрическая статистика и непараметрическая (дескриптивная) статистика.
Первое направление связано с оценкой (определением) неизвестных параметров законов распределения случайных величин на основе экспериментальных наблюдений за значениями случайной величины. Поскольку в качестве оценки выступает число, а числу на числовой прямой соответствует точка, такие оценки называют точечными.
Поскольку точечная оценка получается в результате математических операций над полученными из эксперимента значениями случайной величины она (оценка) сама есть случайная величина, имеющая определенную функцию распределения. Следовательно, точечная оценка должна быть дополнена интервалом, содержащим точечную оценку и возможный разброс её (оценки) значений, которые допустим с наперёд заданной вероятностью, которую называют доверительной. Поэтому наряду с точечными оценками в математической статистике принято определять интервальные оценки или , иными словами, доверительные интервалы, опираясь на уровень доверия или доверительную вероятность
Второе направление в математической статистике связано с проверкой некоторых априорных предположений или статистических гипотез об основных характеристиках экспериментально полученных распределениях случайных величин. Принято называть одну из этих гипотез ( как правило, более важную с практической точки зрения) основной H0, а вторую альтернативной или конкурирующей H1. Индекс 0 буквы H указывает, что гипотеза H0 предполагает несущественное отличие между гипотетическим и истинным значении оцениваемых параметрах, и, наоборот, индекс 1 указывает на существенную разницу между оценкой и истинном значением статистического параметра. Задача проверки статистических гипотез состоит в выборе правила или критерия, позволяющего по результатам наблюдений проверить, справедливость этих гипотез и принять одну из них. Так же, как и при точечной оценке неизвестных параметров, мы не застрахованы от неверного решения, так называемых ошибок первого и второго рода. Ошибка первого рода состоит в том, что мы принимаем конкурирующую гипотезу H1, в то время, как справедлива основная гипотеза H0. Аналогично определяется ошибка второго рода: принимаем основная гипотезу H0, в то время, как справедлива конкурирующая гипотеза H1.
В математической статистике исследуются также байесовские и небайесовские модели. Байесовская модель возникает тогда, когда неизвестный параметр является случайной величиной и имеется априорная информация о его распределении. При байесовском подходе на основе опытных данных априорные вероятности пересчитываются в апостериорные. Этот подход использует формулу Байеса.
Небайесовские модели появляются тогда, когда неизвестный параметр нельзя считать случайной величиной и все статистические выводы приходится делать, опираясь только на результаты «пробных» испытаний. Именно такие модели в основном рассматриваются в математической статистике.
В математической статистике употребляют также понятие параметрической и непараметрической модели. Параметрическая модель возникает тогда, когда нам известен вид функции распределения наблюдаемого признака, но неизвестны её параметры и необходимо по результатам испытаний определить эти параметры (задача оценки неизвестного параметра) или проверить гипотезу о принадлежности его некоторому заранее выделенному множеству значений (задача проверки статистических гипотез). Непараметрическая модель – когда неизвестен вид закона распределения и необходимо с помощью специальных критериев определить к какому классу распределений он относится.
Похожие работы
... , что все это рассуждение основано на предположении о нормальности распределения этих повторных выборок (т.е. нормальности выборочного распределения). Это предположение обсуждается в следующем разделе. Все ли статистики критериев нормально распределены? Не все, но большинство из них либо имеют нормальное распределение, либо имеют распределение, связанное с нормальным и вычисляемое на основе ...
... признак. Классификация. Для изучения общей теории статистики необходимо рассмотреть основные понятия на которых будет основываться все дальнейшее изложение материала. Т.к. статистика имеет дело с массовыми явлениями, то основным понятием является статистическая совокупность. Статистическая совокупность – это множество объектов или явлений изучаемых статистикой, которые имеют один или несколько ...
... пер- вичных статистических материалов, и вторичные, характеризуемые в процессе обработки и анализа данных. ПОКАЗАТЕЛЬ - одно из основных понятий статистики, под которым имеется в виду обобщенная колличественная характеристика социально-экономических явлений и процессов в их качественной определенности в условиях конкрет- ного места и времени. Примерами конкретных социально-экономических показате ...
... . Совокупность заведений, занимающихся однородным видом деятельности, представляет собой отрасль. Для количественного описания состояния и функционирования экономики в системе национальных счетов используются понятия запасов и потоков. Запасы отражают все виды активов и пассивов в экономике и отражаются в учете на определенную дату. Потоки отражают любые действия по созданию, преобразованию, ...
0 комментариев