Навигация
Размах вариации R = 210 – 150 = 60 шт
1. Размах вариации R = 210 – 150 = 60 шт.
2. Среднее линейное отклонение ![]() =
= ![]() шт.
шт.![]()
3. Дисперсия ![]()
![]() = 324.
= 324.
4. Среднее квадратическое отклонение ![]()
![]() = 18 шт.
= 18 шт.
6. Коэффициент вариации ![]()
![]() % = 9,8%.
% = 9,8%.
Как видно из расчётов, коэффициент вариации составляет 9,8% и, следовательно, типичность среднего значения высока.
В ряде задач статистическая совокупность оказывается разделенной на несколько групп. В этом случае вычисляют три вида дисперсий: общую ![]() , межгрупповую
, межгрупповую ![]() и среднюю внутригрупповую дисперсию
и среднюю внутригрупповую дисперсию ![]() .
.
Рассмотрим статистическую совокупность, которая разделена на m групп. (Это разделение может совпадать или не совпадать с группировкой той же совокупности, представленной вариационным рядом, в котором совокупность разделена на k групп). Обозначим количество элементов, попавших в i-ю группу через ![]() (
(![]() ).
).
Общая дисперсия ![]() характеризует рассеяние признака по всей изучаемой совокупности под влиянием всех факторов, формирующих уровень признака у единиц совокупности, и определяется по формуле (5.1)
характеризует рассеяние признака по всей изучаемой совокупности под влиянием всех факторов, формирующих уровень признака у единиц совокупности, и определяется по формуле (5.1)
 , (8)
, (8)
где ![]() – общая средняя арифметическая для всей изучаемой совокупности.
– общая средняя арифметическая для всей изучаемой совокупности.
Межгрупповая дисперсия ![]() отражает различия в величине изучаемого признака, возникающие под влиянием фактора, положенного в основу группировки, и показывает рассеяние групповых средних вокруг средней величины признака в совокупности
отражает различия в величине изучаемого признака, возникающие под влиянием фактора, положенного в основу группировки, и показывает рассеяние групповых средних вокруг средней величины признака в совокупности
![]()
 , (9)
, (9)
где ![]() – средняя арифметическая по i-й группе.
– средняя арифметическая по i-й группе.
Внутригрупповая дисперсия используется для оценки рассеяния признака внутри группы. Она характеризует вариацию, не зависящую от значений признака, положенного в основу группировки (факторного признака), и возникающую под влиянием других факторов. Средняя внутригрупповая дисперсия вычисляется по формуле
![]()
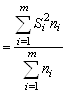 , (10)
, (10)
Здесь 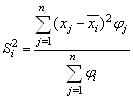 – дисперсия признака в i-й группе, где
– дисперсия признака в i-й группе, где ![]() – частота признака
– частота признака ![]() в i-й группе.
в i-й группе.
Общая, межгрупповая и средняя внутригрупповая дисперсии связаны правилом сложения дисперсий
![]() =
=![]() .
.
Смысл этого соотношения заключается в том, что общая дисперсия, определяемая влиянием всех факторов, равна дисперсии, определяемой фактором группировки, и дисперсии, возникающей под влиянием прочих факторов.
В статистическом анализе вычисляют характеристики, зависящие от распределения частот по вариантам – от структуры распределения. Поэтому эти характеристики получили название структурных средних величин. К таким показателям относятся мода и медиана.
Мода ![]() – значение признака, наиболее часто встречающееся в ряду распределения. Мода определяется различными способами в зависимости от вида вариационного ряда. В дискретном вариационном ряду мода – вариант с максимальной частотой в изучаемой совокупности.
– значение признака, наиболее часто встречающееся в ряду распределения. Мода определяется различными способами в зависимости от вида вариационного ряда. В дискретном вариационном ряду мода – вариант с максимальной частотой в изучаемой совокупности.
Пример. По данным статистического наблюдения получены значения величины X = {5, 3, 1, 2, 1, 4, 1, 5, 2, 1, 4, 2, 1, 1, 6}. Определить моду.
Построим вариационный ряд
| X | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 4 | 4 | 5 | 5 | 6 |
Соответствующий сгруппированный вариационный ряд имеет вид:
| X | 1 | 2 | 3 | 4 | 5 | 6 |
| F | 6 | 3 | 1 | 2 | 2 | 1 |
Значение признака Х, имеющего наибольшую частоту (6) равно 1. Следовательно, для данного вариационного ряда ![]() = 1.
= 1.
При отыскании моды в интервальном ряду сначала определяют модальный интервал – интервал, имеющий наибольшую частоту. Затем мода рассчитывается по формуле
![]()
![]() , (11)
, (11)
где ![]() – нижняя граница модального интервала;
– нижняя граница модального интервала; ![]() – величина модального интервала;
– величина модального интервала; ![]() – частота модального интервала, fm-1 – частота интервала, предшествующего модальному, fm+1 – частота интервала, следующего за модальным.
– частота модального интервала, fm-1 – частота интервала, предшествующего модальному, fm+1 – частота интервала, следующего за модальным.
Пример. По данным статистического наблюдения построен интервальный ряд распределения рабочих по заработной плате
| Зар. плата (руб.) | 1300-1400 | 1400-1500 | 1500-1600 | 1600-1700 | 1700-1800 |
| Число рабочих (частота) | 20 | 40 | 55 | 60 | 35 |
| Кумулятивная частота | 20 | 60 | 115 | 175 | 210 |
Найти моду.
Модальным интервалом является интервал (1600-1700). Подставив данные таблицы в формулу (5.5), получим
o = ![]() 1616,7 руб.
1616,7 руб.
Медиана ![]() – значение признака (вариант), которое делит вариационный ряд на две равные части, одна из которых – со значениями признака меньше медианы, вторая – со значениями признака больше медианы.
– значение признака (вариант), которое делит вариационный ряд на две равные части, одна из которых – со значениями признака меньше медианы, вторая – со значениями признака больше медианы.
Медиана для дискретных и интервальных вариационных рядов определяется по-разному. Если дан дискретный несгруппированный вариационный ряд и число вариантов n нечетно, то ![]() =
=![]() , где
, где ![]() ; если число вариантов n четное,
; если число вариантов n четное, ![]() = ( x
= ( x![]() + x
+ x ![]() ) / 2, где
) / 2, где![]()
![]() .
.
Пример. По данным примера 5.2 найти медиану дискретного вариационного ряда.
Число вариантов n несгруппированного ряда равно 15, следовательно, k = (n + 1)/2 = 8, и медиана равна 2.
Пример 5.3. Определить медиану по данным, приведенным в таблице
| Размер заработной платы (тыс. руб.) | Число работников (частота) | Накопленная частота | |
| 5800 | 30 | 30 | |
| 6000 | 45 | 75 | |
| 6200 | 80 | 155 | |
| 6400 | 60 | 215 | |
| 6600 | 35 | 250 |
Решение. Сумма частот n = 250 – четно, ![]() = 125.
= 125. ![]()
![]()
![]() = 6200.
= 6200.
В интервальном вариационном ряду для определения медианы сначала нужно найти медианный интервал – первый по счету интервал, в котором накопленная частота равна или превышает полусумму частот вариационного ряда. После этого медиана определяется по формуле
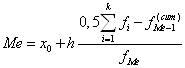 ,
,
где ![]() – нижняя граница медианного интервала;
– нижняя граница медианного интервала;
![]() – величина медианного интервала;
– величина медианного интервала;
![]() – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
![]() – частота медианного интервала.
– частота медианного интервала.
Пример. По данным примера 5.3 определить медиану интервального ряда.
Медианным является интервал (1500-1600), так как это первый по счету интервал, сумма накопленных частот которого (115) больше полусуммы накопленных частот интервального ряда (0.5∙210 = 105). Подставив данные примера в формулу для медианы интервального ряда, получим
![]() .
.
В математической статистике используют структурные характеристики, делящие вариационный ряд на большее число частей, – квантили – показатели дифференциации признаков по частотам. Различают несколько видов квантилей.
Квартили – значения признака, которые делят вариационный ряд на четыре равные части. Второй квартиль равен медиане, первый и третий вычисляются аналогично расчету медианы. При расчете i-го квартиля сначала по относительным частотам определяют соответствующий квартильный интервал – первый по счету интервал, накопленная частота которого больше ![]() (n – сумма частот). Затем значение квартиля рассчитывают по формуле, аналогичной формуле для нахождения медианы
(n – сумма частот). Затем значение квартиля рассчитывают по формуле, аналогичной формуле для нахождения медианы
 , i =1, 2, 3,
, i =1, 2, 3,
где i – номер квартильного интервала;
![]() – нижняя граница i-го квартильного интервала;
– нижняя граница i-го квартильного интервала;
![]() – величина i-го квартильного интервала;
– величина i-го квартильного интервала;
![]() – накопленная частота интервала, предшествующего i-му квартильному интервалу;
– накопленная частота интервала, предшествующего i-му квартильному интервалу;
![]() – частота i-го квартильного интервала.
– частота i-го квартильного интервала.
Отношение третьего и первого квартилей называется квартильным коэффициентом
![]() =
=![]()
и показывает, во сколько раз значение признака у четверти вариантов, имеющих наибольшие значения признака, превышает значение признака у другой четверти с наименьшими значениями.
Значения признака, которые делят вариационный ряд на десять равных частей, называются децилями. Расчет значений децилей проводится аналогично расчету квартилей. Отношение девятого и первого децилей – децильный коэффициент ![]() =
= ![]() показывает, во сколько раз величина признака у 10% совокупности с наибольшими значениями превышает такую же величину у 10% совокупности с наименьшими значениями признака.
показывает, во сколько раз величина признака у 10% совокупности с наибольшими значениями превышает такую же величину у 10% совокупности с наименьшими значениями признака.
В статистике используются также перцентили – значения признака, которые делят вариационный ряд на сто равных частей.
В ряде случаев в математической статистике вычисляют показатели формы распределения частот по вариантам: асимметрию и эксцесс. Характеристика симметричности распределения – коэффициент асимметрии – рассчитывается по формуле
![]() ,
,
где 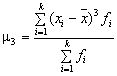 – центральный момент третьего порядка;
– центральный момент третьего порядка;
![]() – куб среднего квадратического отклонения.
– куб среднего квадратического отклонения.
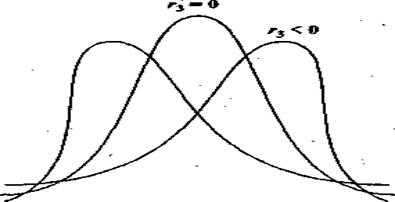
Если варианты распределены симметрично относительно средней величины ![]() , т.е. равноудаленные от
, т.е. равноудаленные от ![]() варианты имеют одинаковые частоты, коэффициент асимметрии равен нулю. Если
варианты имеют одинаковые частоты, коэффициент асимметрии равен нулю. Если ![]() < 0, в вариационном ряду преобладают варианты, которые меньше, чем средняя величина. В этом случае говорят о наличии левосторонней асимметрии. И, наоборот, при
< 0, в вариационном ряду преобладают варианты, которые меньше, чем средняя величина. В этом случае говорят о наличии левосторонней асимметрии. И, наоборот, при ![]() > 0 преобладают варианты, которые больше
> 0 преобладают варианты, которые больше ![]() . Это указывает на правостороннюю симметрию.
. Это указывает на правостороннюю симметрию.
Пример. Рис. 1 иллюстрирует зависимость вида кривой распределения от асимметрии.
|
Рис. 1
Для симметричных распределений рассчитывается также эксцесс распределения – показатель островершинности распределения. Эксцесс рассчитывается по формуле
![]() ,
,
где 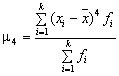 – центральный момент четвертого порядка.
– центральный момент четвертого порядка.
При расчете экцесса эталоном является нормальное распределение, для которого ![]() , и, следовательно
, и, следовательно ![]() . Для распределений, у которых
. Для распределений, у которых ![]() , кривая более островершинная, чем нормальная кривая. Если
, кривая более островершинная, чем нормальная кривая. Если ![]() , кривая будет более плосковершинной.
, кривая будет более плосковершинной.
Пример. Рис. 2 иллюстрирует зависимость вида кривой распределения от эксцесса
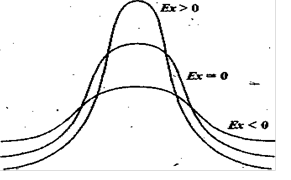
Рис. 2
Контрольные вопросы
1. Что называется средней величиной?
2. Какие виды средних величин вы знаете?
3. Какие виды средней арифметической вам известны?
4. Как вычисляется средняя геометрическая величина?
5. Что представляет собой средняя гармоническая?
6. Чем характеризуется понятие «размах вариации»?
7. Что такое среднее линейное отклонение?
8. Что такое дисперсия и как она может быть вычислена?
9. Что называется средним квадратическим отклонением?
10.Что называется коэффициентом вариации?
11.Что такое мода?
12.Как определяется мода для дискретных и интервальных вариационных рядов?
13.Что такое медиана?
14.Как определяется медиана для дискретных и интервальных вариационных рядов?
4.Графическое представление вариационных рядов
В математической статистике широко используется геометрическая интерпретация результатов первичной статистической обработки экспериментальных данных. Графическое представление сгруппированного дискретного вариационного ряда в осях – признак и частота - называется полигоном частот. Графическое представление интервального вариационного ряда в виде прямоугольников, с основаниями, равными длине интервалов и с высотой, равной соответствующей относительной частоте, называется гистограммой.
Пример. Имеются данные наблюдения над числом посетителей сайта академии в течение 40 дней:
70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100, 120, 120, 100, 75, 75, 70, 70, 100, 100, 75.
Число посетителей Х является дискретным признаком, полученные данные представляют собой выборку из n = 40 наблюдений.
Требуется составить вариационный ряд, найти относительные частоты, построить эмпирическую функцию плотности распределения и эмпирическую функцию распределения.
Сначала составим вариационный ряд:
60, 60, 60, 65, 65, 65 70, 70, 70, 70, 70, 70, 70, 75, 75, 75, 75, 75, 75, 75, 75, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 120, 120, 120, 120, 120, 120.
Сгруппированный вариационный ряд представим в виде таблиц
| Номер группы | i | 1 | 2 | 3 | 4 | 5 | 6 |
| Число посетителей | хi | 60 | 65 | 70 | 75 | 100 | 120 |
| Частота | ni | 3 | 3 | 9 | 8 | 11 | 6 |
| Относительная частота | pi* | 0.075 | 0.075 | 0.225 | 0.2 | 0.275 | 0.15 |
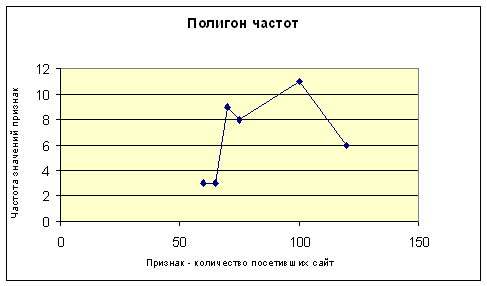
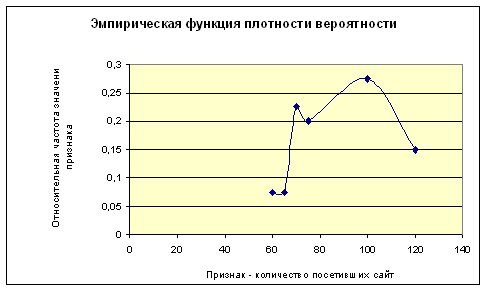
Рис.4
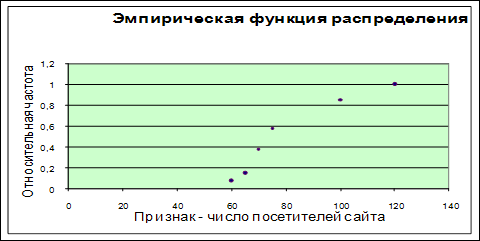
Построим эмпирическую функцию распределения. Исходными данными для её построения являются множество значений признака и множество относительных частот:
| хi | 50 | 60 | 65 | 70 | 75 | 100 | 120 | ||
| pi* | 0 | 0.075 | 0.075 | 0.225 | 0.2 | 0.275 | 0.15 | ||
| xi | 50 | 60 | 65 | 70 | 75 | 100 | 120 | ||
| Pi* | 0 | 0,075 | 0,075 | 0,225 | 0,200 | 0,275 | 0,150 | ||
| F ( xi ) | 0 | 0,075 | 0,15 | 0,375 | 0,575 | 0,85 | 1 | ||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
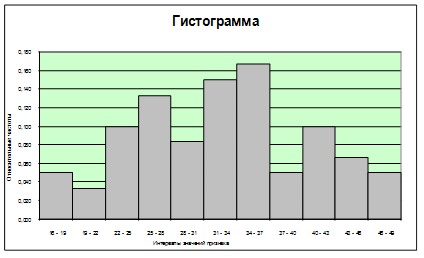
Пример. В таблице 1 приведена выборка результатов отчетности однотипных 60 предприятий по прибыли (млн. руб.). Составить интервальный вариационный ряд. Построить гистограмму.
Таблица 1.
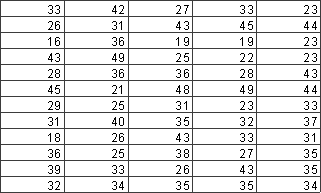
Результаты решения задачи приведены в таблице 2.
Таблица 2.
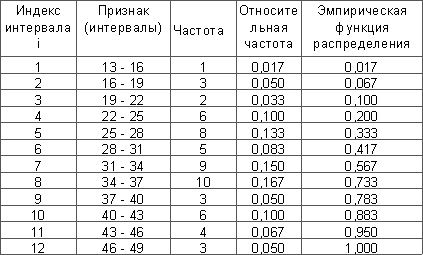
Контрольные вопросы:
1. Дайте определения основным категориям математической статистике: генеральная совокупность, выборка, статистическая совокупность, признак, оценка.
2. Что называется вариационным рядом? Классификация вариационных рядов.
3. Выпишите основные соотношения для вычисления количественных статистических характеристик вариационного ряда: среднего арифметического значения, дисперсии, среднего квадратического значения, коэффициента вариации, коэффициента асимметрии, коэффициента эксцесса, моды, медианы
Похожие работы
... , что все это рассуждение основано на предположении о нормальности распределения этих повторных выборок (т.е. нормальности выборочного распределения). Это предположение обсуждается в следующем разделе. Все ли статистики критериев нормально распределены? Не все, но большинство из них либо имеют нормальное распределение, либо имеют распределение, связанное с нормальным и вычисляемое на основе ...
... признак. Классификация. Для изучения общей теории статистики необходимо рассмотреть основные понятия на которых будет основываться все дальнейшее изложение материала. Т.к. статистика имеет дело с массовыми явлениями, то основным понятием является статистическая совокупность. Статистическая совокупность – это множество объектов или явлений изучаемых статистикой, которые имеют один или несколько ...
... пер- вичных статистических материалов, и вторичные, характеризуемые в процессе обработки и анализа данных. ПОКАЗАТЕЛЬ - одно из основных понятий статистики, под которым имеется в виду обобщенная колличественная характеристика социально-экономических явлений и процессов в их качественной определенности в условиях конкрет- ного места и времени. Примерами конкретных социально-экономических показате ...
... . Совокупность заведений, занимающихся однородным видом деятельности, представляет собой отрасль. Для количественного описания состояния и функционирования экономики в системе национальных счетов используются понятия запасов и потоков. Запасы отражают все виды активов и пассивов в экономике и отражаются в учете на определенную дату. Потоки отражают любые действия по созданию, преобразованию, ...
0 комментариев