Навигация
При увеличении объёма выборки оценка должна сходиться по вероятности к истинному значению параметра. В этом случае оценку называют состоятельной
2. При увеличении объёма выборки оценка должна сходиться по вероятности к истинному значению параметра. В этом случае оценку называют состоятельной.
3. Оценка параметра представляет собой случайную величину, зависящую от выборки, поэтому естественный интерес представляет разброс этой оценки, т.е. её дисперсия. Оценку называют эффективной, если при заданном объёме выборки эта оценка имеет наименьшую дисперсию.
Поскольку в качестве оценки мы ищем число – точку на координатной оси – то такие оценки называются точечными.
2. Методы оценивания: метод моментов, метод максимального правдоподобия (Фишера), метод наименьших квадратов
Известны три основных метода нахождения приближенных формул вычисления точечных оценок: метод максимального правдоподобия, метод моментов и метод наименьших квадратов.
Метод максимального правдоподобия (Фишера)Пусть исследуемый нами признак Х имеете непрерывное распределение, зависящее от m параметров Θ1….Θm из некоторого множества Θ. В этом случае плотность вероятности генеральной совокупности будет зависеть от значения признака х и этих параметров, т.е. ƒ(х, Θ1….Θm). Пусть теперь из генеральной совокупности получена выборка объёмом n: х1, …..хn. Рассмотрим представленную выборку с позиции того, что каждое значение её хi есть реализация некоторой случайной величины Хi, полученное в i-ом наблюдении, причем в силу репрезентативности выборки Хi имеет то же распределение, что и вся генеральная совокупность. В результате выборку можно рассматривать как n –мерную случайную величину (Х1, …. Хn) или выборочный вектор Х = (Х1…. Хn), все компоненты которого представляют независимые случайные величины с одинаковыми функциями плотности вероятности, совпадающими с плотностью вероятности генеральной совокупности, т.е.
ƒ Хi (хi, Θ1….Θm) = ƒ(хi, Θ1….Θm)
Из теории вероятностей известно, что плотность вероятностей совместного распределения независимых случайных величин равна произведению плотностей вероятностей каждой из случайных величин, т.е.
ƒ(х1, х2, ….хn, Θ1….Θm) = ƒ(х1, Θ1….Θm) ƒ(х2, Θ1….Θm)….. ƒ(хn, Θ1….Θm)
Метод максимального правдоподобия оценки неизвестных параметров распределения
Θ1….Θm основан на свойстве случайной величины реализовывать в эксперименте в основном те свои значения (Х1, …. Хn) , вероятность которых максимальная.
Таким образом, в качестве оценки ![]() неизвестных параметров распределения Θ1….Θm принимаются те значения, которые доставляют max функции ƒ(х1, х2, ….хn, Θ1….Θm), т.е. решения уравнения :
неизвестных параметров распределения Θ1….Θm принимаются те значения, которые доставляют max функции ƒ(х1, х2, ….хn, Θ1….Θm), т.е. решения уравнения :
ƒ(х1, х2, ….хn, ![]() ) = max ƒ(х1, х2, ….хn, Θ1….Θm),
) = max ƒ(х1, х2, ….хn, Θ1….Θm),
( Θ1….Θm )![]() Θ
Θ
если решения этого уравнения существуют.
Во многих случаях вместо функции ƒ(х1, х2, ….хn, Θ1….Θm) рассматривают её натуральный логарифм, достигающий максимума в тех же точках, что и сама функция ƒ(х1, х2, ….хn, Θ1….Θm). В результате нахождение оценок ![]() сводится к известной задаче математического анализа - отыскания максимума функции m переменных. Для отыскания точек экстремумов получаем уравнения максимального правдоподобия:
сводится к известной задаче математического анализа - отыскания максимума функции m переменных. Для отыскания точек экстремумов получаем уравнения максимального правдоподобия:![]()
![]() или
или ![]() i = 1….m
i = 1….m
Пример. Пусть время t до выхода из строя группы компьютеров на испытательном стенде описывается показательным распределением:
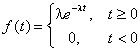 ,
,
единственный параметр которого λ неизвестен. Найти методом максимального правдоподобия оценку параметра λ
Р е ш е н и е. Испытав n компьютеров, мы получим выборку объёмом n : t1, ….tn. Функция плотности вероятности совместного распределения значений t1, ….tn имеет вид:
ƒ(t1, t2, ….tn, λ) = λe-λt1 λe-λt2…. λe-λtn = λn e-λt1 e-λt2…. e-λtn
поскольку выражение для функции плотности вероятности представляет собой произведение экспонент, то лучше воспользоваться логарифмической формой функции правдоподобия:
ln ƒ(t1, t2, ….tn, λ) = ln [λn e-λt1 e-λt2…. e-λtn ] = n lnλ – λ (t1 + t2 + ….+ tn).
Уравнение максимального правдоподобия будет иметь вид:
![]()
![]()
![]() – (t1 + t2 + ….+ tn) = 0
– (t1 + t2 + ….+ tn) = 0 ![]()
![]()
Как было установлено в теории вероятностей, математическое ожидание для показательного распределения равно М(Х) = ![]() и обозначая
и обозначая ![]() , получим:
, получим:
![]()
Пример. Пусть интересующая нас случайная величина распределена по нормальному закону с неизвестными параметрами Мх и σ (математическое ожидание и среднеквадратическое отклонение) и получена выборка на основе опытов объёмом n : х1, …..хn. Найти методом максимального правдоподобия оценку параметров Мх и σ.
Р е ш е н ие. Плотность вероятности совместного распределения значений х1, …..хn независимых нормально распределённых случайных величин имеет вид:
ƒ(х1, х2, ….хn, Мх, σ) =
![]()
![]() …..
…..![]() =
=
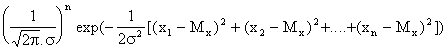 =
=
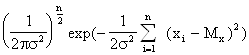
Воспользуемся логарифмической формой представления функции правдоподобия:
ln ƒ(х1, х2, ….хn, Мх, σ) = - ![]() ln 2π -
ln 2π - ![]() ln σ2
ln σ2 ![]() =
=
- ![]() ln 2π -
ln 2π - ![]() ln D
ln D ![]()
Обозначим σ2 = D – дисперсию распределения признака Х. Уравнения максимального правдоподобия для оценки параметров Мх и σ2 = D имеют вид:
![]()
![]() -
-![]() = 0
= 0
Решения этой системы дают оценки параметров:
![]()
![]()
Пример. Найти методом максимального правдоподобия оценку параметра λ в распределении Пуассона ![]() на основе проведенных опытов.
на основе проведенных опытов.
Решение. Будем называть опытом группу из n испытаний. При этом в каждом опыте фиксируем число появления рассматриваемого события. Пусть таких независимых опытов будет к. Обозначим число появлений события в i-м опыте mi.Функция плотности вероятности совместного распределения количества появления рассматриваемого события m1, m2,…. mk имеет вид:
ƒ(m1, m2, ….mn, λ) =
![]()
![]() …….
…….![]() =
= 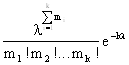
Находим логарифм этой функции:
Ln ƒ(m1, m2, ….mn, λ) =Возьмём первую производную по λ и приравняем её к нулю. Получим уравнение максимального правдоподобия:
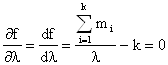 ,
,
откуда ![]()
Если взять вторую производную
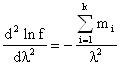
то оказывается, что она отрицательная. Это значит, что при полученном значении ![]() функция правдоподобия lnƒ(m1, m2, ….mn, λ) достигает максимума.
функция правдоподобия lnƒ(m1, m2, ….mn, λ) достигает максимума.
Вывод. Метод максимального правдоподобия является эффективным в случае малых выборок, но часто требует довольно сложных вычислений.
Метод моментов (Пирсона)Идея метода моментов заключается в приравнивании теоретических и соответствующих им эмпирических моментов, причём число моментов и, следовательно, число уравнений для определения неизвестных параметров распределений берется равным числу параметров. Покажем применение метода на тех же примерах, что и предыдущем пункте.
Напомним, что для случайной величины определены её числовые характеристики – начальные и центральные моменты. Для дискретной случайной величины:
теоретическим моментом к-го порядка называется соотношение вида:
Мкт = ![]() .
.
Эмпирическим моментом к-го порядка для несгруппированных данных называется соотношение вида:
Мкэ = 
Если принять А = 0, то моменты в этом случае называются начальными. Обычно их обозначают малыми латинскими буквами.
![]() ,
, 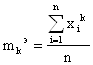 .
.
Например, начальный момент первого порядка m1 - есть математическое ожидание.
Если принять А = m1, то моменты называются центральными. Обычно их обозначают малыми греческими буквами.
μк T =![]() , μк Э =
, μк Э =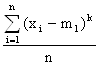 .
.
Например, μ2 - есть дисперсия.
В случае непрерывных случайных величин в теоретических моментах суммы заменяются интегралами с бесконечными пределами.
Пример. Для показательного распределения единственным параметром является λ. Для его оценивания нужно одно уравнения. Возьмем, например, приравняем первые начальные моменты – теоретический и эмпирический.
Первый начальный теоретический момент получается интегрированием по частям выражения:
m1Т = 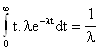
Первый начальный эмпирический момент имеет вид: m1Э =![]()
Приравняем их:
m1Э = m1Т![]()
![]() =
= ![]()
![]()
![]() =
= 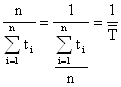
Пример. Для нормального распределения, определенного двумя параметрами, Мх и σ, приравняем теоретический и эмпирический моменты первого порядка и центральные моменты второго порядка: m1T = Mx, μ2T = σ2
m1Э = ![]() , μ2Э =
, μ2Э = 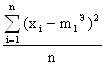
отсюда
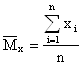 ,
, ![]()
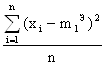 =
= 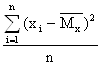
или 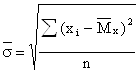
В ы в о д ы. В рассмотренных примерах оценки, полученные методом максимального правдоподобия и моментов, совпали, однако этот факт не является общим. Для других распределений оценки, полученные различными методами, могут не совпадать.
Итак, оценками двух основных параметров генеральной совокупности,– математического ожидания и дисперсии являются:
- для математического ожидания - выборочная средняя, определяемая как среднее арифметическое полученных по выборке значений:
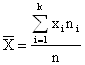 ,
,
где xi – варианта выборки, ni – частота повторяемости варианты, n – объём выборки
- собой среднюю арифметическую квадратов отклонений вариант от их выборочной для дисперсии – выборочная дисперсия, представляющая средней:
d = 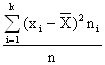 .
.
Для расчетов может быть использована также эквивалентная формула, получающаяся после возведения в квадрат и почленного суммирования:
d = ![]() ,
,
где ![]() - выборочная средняя квадратов вариант выборки.
- выборочная средняя квадратов вариант выборки.
После получения оценок с помощью любого из вышеприведенного метода остается нерешенным важнейший вопрос о несмещенности и эффективности оценок. Этот вопрос для математического ожидания решается положительно, т.е. ![]() - несмещенная оценка для Мх. Для дисперсии – отрицательно, т.е. d является смещенной оценкой для D = σ2.
- несмещенная оценка для Мх. Для дисперсии – отрицательно, т.е. d является смещенной оценкой для D = σ2.
Для устранения смещенности выборочной дисперсии её следует умножить на величину n/(n-1) и получим:
S2 =Пример. Покажем, что оценка математического ожидания с помощью выборочной средней является несмещенной.
Решение. Оценка параметра называется несмещенной, если математическое ожидание оценки равно оцениваемому параметру. Покажем , что математическое ожидание среднего арифметического равно математическому ожиданию генеральной совокупности. М(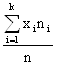 ) =
) = 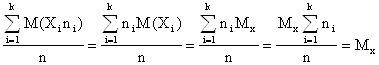 ,
, т.к. ![]()
Замечание. Мы воспользовались представлением выборочных значений как компонентов к – мерной случайной величины (x1, x2,…..xk) → (X1, X2,….Xk)
( см. начало обсуждение метода максимального правдоподобия).
Пример. Покажем, что оценка дисперсии является смещенной.
Воспользуемся расчётной формулой для вычисления оценки дисперсии, приведенной выше:
d = ![]() ,
,
![]()
![]()
![]()
![]() d =
d = 
здесь n2 слагаемых здесь по n слагаемых
здесь n слагаемых
здесь (n2 – n) слагаемых
= ![]()
Вычислим математическое ожидание d, снова воспользовавшись представлением выборочных данных n –мерной случайной величиной (x1, x2,…..xn) → (X1, X2,….Xn):
М(d) = M(![]() ) =
) = ![]() -
- ![]() .
.
С учётом количества слагаемых (см. выше) и того, что М(Хi) = M(Xj) = M(X) и М(ХiXj) = М(Хi) M(Xj) в силу статистической независимости Хi и Xj получаем:
М(d) =![]()
![]()
где использована формула для вычисления дисперсии: D =![]()
Из полученного результата следует, что выборочная дисперсия d является смещенной оценкой для D, т.к. её математическое ожидание не равно D, а несколько меньше. Чтобы ликвидировать это смещение, достаточно умножить d на ![]() . Результат этого умножения обозначенный S2 и называется “исправленной эмпирической дисперсией”.
. Результат этого умножения обозначенный S2 и называется “исправленной эмпирической дисперсией”.
Пример. На предприятии изготовляется определённый вид продукции. Ежемесячный объём выпуска этой продукции является случайной величиной, для характеристики которой принят показательный закон распределения.
![]() ( x ≥ 0 )
( x ≥ 0 )
В течение шести месяцев проводился замер объёмов выпуска продукции, получены следующие данные:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 |
| Объём выпуска | 25 | 34 | 23 | 28 | 32 | 30 |
Найти оценку параметру λ.
Решение. Так как закон распределения содержит лишь один параметр λ, то для его оценке надо составить одно уравнение, например, равенство теоретического и эмпирического первых начальных моментов. Находим выборочную среднюю - эмпирический первый начальный момент:
![]() = (25+34+23+28+32+30)/6 = 28.7
= (25+34+23+28+32+30)/6 = 28.7
Определяем математическое ожидание – теоретический первый начальный момент:
М(Х) =
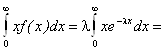
Приравниваем теоретический и эмпирический первые начальные моменты:
![]()
откуда получаем оценку параметра λ:
![]()
Похожие работы
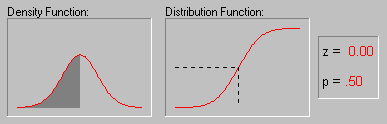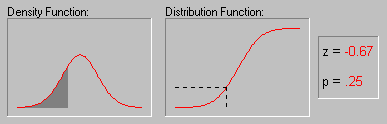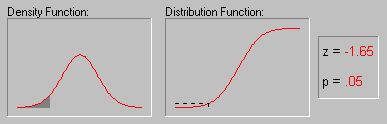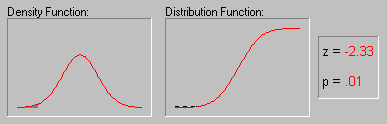
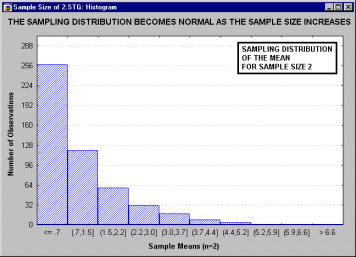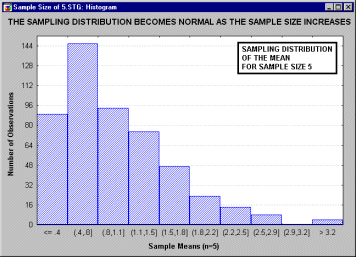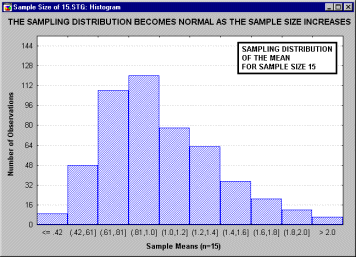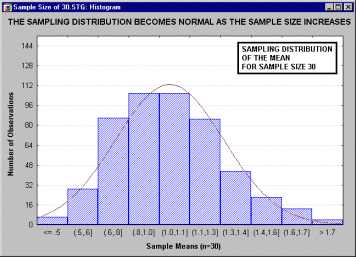
... , что все это рассуждение основано на предположении о нормальности распределения этих повторных выборок (т.е. нормальности выборочного распределения). Это предположение обсуждается в следующем разделе. Все ли статистики критериев нормально распределены? Не все, но большинство из них либо имеют нормальное распределение, либо имеют распределение, связанное с нормальным и вычисляемое на основе ...
... признак. Классификация. Для изучения общей теории статистики необходимо рассмотреть основные понятия на которых будет основываться все дальнейшее изложение материала. Т.к. статистика имеет дело с массовыми явлениями, то основным понятием является статистическая совокупность. Статистическая совокупность – это множество объектов или явлений изучаемых статистикой, которые имеют один или несколько ...
... пер- вичных статистических материалов, и вторичные, характеризуемые в процессе обработки и анализа данных. ПОКАЗАТЕЛЬ - одно из основных понятий статистики, под которым имеется в виду обобщенная колличественная характеристика социально-экономических явлений и процессов в их качественной определенности в условиях конкрет- ного места и времени. Примерами конкретных социально-экономических показате ...
... . Совокупность заведений, занимающихся однородным видом деятельности, представляет собой отрасль. Для количественного описания состояния и функционирования экономики в системе национальных счетов используются понятия запасов и потоков. Запасы отражают все виды активов и пассивов в экономике и отражаются в учете на определенную дату. Потоки отражают любые действия по созданию, преобразованию, ...
0 комментариев