Равномерное распределение
Условные законы распределения, условные числовые характеристики системы случайных величин, условие независимости случайных величин
Корреляция, свойство коэффициента корреляции. Линейная корреляция
Предельные теоремы теории вероятностей. Центральная предельная теорема Ляпунова
Основные категории статистики
Методы первичного анализа экспериментальных данных. Построение вариационных рядов и определение их основных характеристик
Размах вариации R = 210 – 150 = 60 шт
Сформулируйте определения полигона частот, гистограммы и кумуляты
При увеличении объёма выборки оценка должна сходиться по вероятности к истинному значению параметра. В этом случае оценку называют состоятельной
Статистики. Критерии. Критериальные случайные величины Пирсона, Стьюдента, Фишера-Снедекора
Навигация
Основные категории статистики
Основные понятия статистики
86945
знаков
23
таблицы
25
изображений
2. Основные категории статистики
Основными категориями математической статистики являются: генеральная совокупность, выборка, теоретическая и эмпирическая функции распределения.
Определение 1. Пусть имеется совокупность N объектов любой природы, над которыми проводятся наблюдения или совокупность всех возможных наблюдений. Каждое из наблюдений характеризуется определенным значением хi (среди которых могут быть и одинаковые) некоторого общего для всех объектов признака (характеристики) Х. Назовём множество всех изучаемых объектов генеральной совокупностью, где N - объём генеральной совокупности.
В математической статистике обычно рассматривается генеральная совокупность бесконечно большого объёма.
Определение 2. Выборочной совокупностью или выборкой назовем n объектов, отобранных из генеральной совокупности и подвергнутые исследованию, число n – объёмом выборки.
Выборка должна обладать свойством репрезентативности, В силу закона больших чисел, можно утверждать, что выборка репрезентативна, если каждый её объект выбран из генеральной совокупности случайным образом, т.е. все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.
Определение 3. Эмпирическая функция распределения. Пусть из генеральной совокупности извлечена выборка объёма n , причём количественный признак х1 наблюдался n1 раз, …хk - nk раз. Очевидно,
.
Наблюдаемые значения количественного признака хi называются вариантами, а ранжированная (записанная в порядке возрастания) последовательность вариант,, - вариационным рядом. Если исследуемый признак принимает дискретные значения, то такой ряд называется дискретным вариационным рядом; если же значения признака являются непрерывными, то вводят интервалы значений признака [хi, хi+1 ] и вариационный ряд называют интервальным. В вычислительных процедурах с интервальными вариационными рядами интервалы [хi, хi+1 ] заменяются серединами интервалов – х*i.
Числа ni называются частотами, а отношение ni к объёму выборки n –относительной частотой. В случае дискретного ряда ni – число повторения значения признака хi , в случае же интервального вариационного ряда ni число вариант, попавших в интервал [хi, хi+1 ]
Соответствие между вариантами, записанных в порядке возрастания и относительными частотами называется эмпирическим (статистическим) распределением выборки
| Х | х1 | х2 | ….. | хк |
| P* | p1* | p2* | ….. | pк* |
Существует полная аналогия между эмпирическим распределением и законом распределения дискретной случайной величины, но в данном случае вместо значений случайной величины фигурируют варианты, а вместо вероятностей – относительные частоты. Если обозначить n(x) – число вариант, меньших x, то эмпирическая функция распределения будет иметь вид:
F*(x) = p* ( X < x ) =
Итак, выборочной (эмпирической) функцией распределения называется функция F*(x), задающая для каждого значения х относительную частоту события Х < x. Выборочную (эмпирическую) функцию распределения можно задать таблично или графически.
Определение 4. Функция распределения генеральной совокупности F (x) называется теоретической функцией распределения.
В отличие от эмпирической функции F*(x) теоретической функцией распределения
F (x) определяет вероятность события X < x , а F*(x) его относительную частоту. Относительные частоты pi* в соответствии с теоремой Бернулли при стремлении объёма выборки n → ∞ сходится по вероятности к вероятности pi. Поэтому в математической статистике эмпирическую функцию F*(x) используют для приближённого представления теоретической функции распределения F (х).
Похожие работы
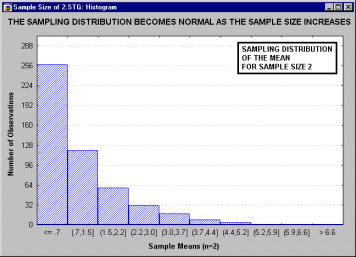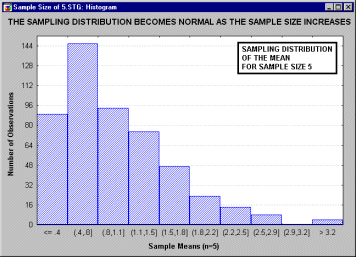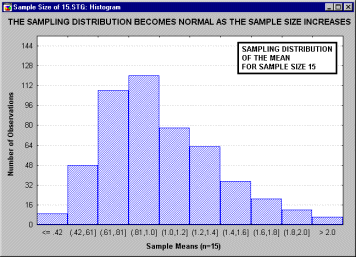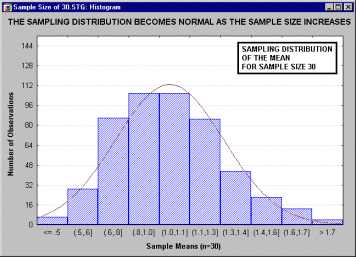
... , что все это рассуждение основано на предположении о нормальности распределения этих повторных выборок (т.е. нормальности выборочного распределения). Это предположение обсуждается в следующем разделе. Все ли статистики критериев нормально распределены? Не все, но большинство из них либо имеют нормальное распределение, либо имеют распределение, связанное с нормальным и вычисляемое на основе ...
... признак. Классификация. Для изучения общей теории статистики необходимо рассмотреть основные понятия на которых будет основываться все дальнейшее изложение материала. Т.к. статистика имеет дело с массовыми явлениями, то основным понятием является статистическая совокупность. Статистическая совокупность – это множество объектов или явлений изучаемых статистикой, которые имеют один или несколько ...
... пер- вичных статистических материалов, и вторичные, характеризуемые в процессе обработки и анализа данных. ПОКАЗАТЕЛЬ - одно из основных понятий статистики, под которым имеется в виду обобщенная колличественная характеристика социально-экономических явлений и процессов в их качественной определенности в условиях конкрет- ного места и времени. Примерами конкретных социально-экономических показате ...
... . Совокупность заведений, занимающихся однородным видом деятельности, представляет собой отрасль. Для количественного описания состояния и функционирования экономики в системе национальных счетов используются понятия запасов и потоков. Запасы отражают все виды активов и пассивов в экономике и отражаются в учете на определенную дату. Потоки отражают любые действия по созданию, преобразованию, ...
0 комментариев