Навигация
1.1 Задачи
Задача №1.1.1. Докажите, что пересечение двух или нескольких выпуклых фигур есть выпуклая фигура.
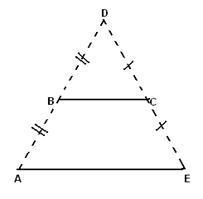
Задача №1.1.2. Докажите, что всякий выпуклый многоугольник является пересечением конечного числа полуплоскостей (рис.1.1.24). [8, 14]
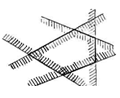
Рис. 1.1.24
Задача №1.1.3. Докажите, что
а) если А и В — внутренние точки выпуклой фигуры Ф, то все точки отрезка АВ — внутренние точки Ф;
б) если А — внутренняя, а В — граничная точка выпуклой фигуры Ф, то все точки отрезка АВ, кроме В,— внутренние точки Ф;
в) если А и В—граничные точки выпуклой фигуры Ф, то либо все точки отрезка АВ — граничные точки Ф, либо все точки отрезка АВ, кроме А и В,— внутренние точки Ф.
Задача №1.1.4. Докажите, что всякая прямая, проведенная через внутреннюю точку выпуклой фигуры, пересекает ее границу не более, чем в двух точках. Если выпуклая фигура ограничена, то каждая прямая, проходящая через какую-либо ее внутреннюю точку, пересекает границу фигуры ровно в двух точках.
Задача №1.1.5. Докажите, что если всякая прямая, проходящая через любую внутреннюю точку ограниченной фигуры, пересекает ее границу в двух точках, то фигура выпукла. [8, 15]
Задача №1.1.6. Докажите, что каждая из двух параллельных опорных прямых, расстояние между которыми имеет наибольшее возможное значение, содержит единственную точку границы фигуры и что отрезок, соединяющий эти точки, перпендикулярен к обеим опорным прямым (рис. 1.1.25). [8, 20]
![]()
Рис. 1.1.25
Задача №1.1.7. Докажите, что наибольшее расстояние между двумя точками выпуклой фигуры совпадает с наибольшим расстоянием между парой параллельных опорных прямых.
Задача №1.1.8. Докажите, что если А и В — две точки выпуклой фигуры Ф, расстояние d между которыми имеет наибольшее значение, то прямые, проведенные через точки А и В перпендикулярно к отрезку АВ, являются опорными прямыми Ф. [8, 21]
1.2 Решения
Задача №1.1.1
Пусть Ф1 и Ф2 — две выпуклые фигуры, Ф — их пересечение, А и В — две произвольные точки, принадлежащие пересечению Ф (рис. 1.1.26). По определению пересечения двух фигур обе точки А и В принадлежат как фигуре Ф1, так и фигуре Ф2. В силу выпуклости фигуры Ф1 все точки отрезка АВ принадлежат Ф1, а в силу выпуклости Ф2 — все они принадлежат также фигуре Ф2. Следовательно, отрезок АВ целиком принадлежит пересечению Ф фигур Ф1 и Ф2, а это и означает, что пересечение Ф выпукло.
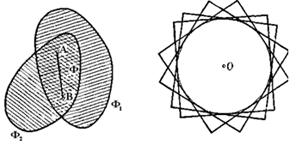
Рис. 1.1.26 Рис. 1.1.27
Точно так же доказывается, что пересечения Ф нескольких выпуклых фигур Ф1, Ф2, ..., Фп выпукло: если А и В — две произвольные точки Ф, то А и В принадлежат одновременно всем фигурам Ф1, Ф2, ..., Фп и в силу того, что все эти фигуры выпуклы, все точки отрезка АВ принадлежат одновременно всем фигурам Ф1, Ф2,..., Фn, т.е. принадлежат их пересечению Ф.
Примечание. Теорема остается верной и в том случае, когда фигур Ф1,…,Фn,... бесконечно много; доказательство ее остаётся прежним. Например, на рис. 1.1.27 изображены равные между собой квадраты с общим центром. Легко видеть, что пересечением всех таких квадратов (а этих квадратов бесконечно много) является круг, т. е. выпуклая фигура.
Задача №1.1.2
Выпуклый многоугольник Ф лежит по одну сторону от каждой прямой, являющейся продолжением его стороны. В самом деле, если бы существовала точка С, принадлежащая Ф и расположенная не с той стороны прямой АВ (А и В — две соседние вершины Ф), с какой многоугольник Ф примыкает к стороне АВ (рис. 1.1.28), то, например, отрезок МС, соединяющий внутреннюю точку М отрезка АВ с точкой С, не принадлежал бы целиком Ф, т. е. многоугольник Ф не мог бы быть выпуклым. Таким образом, выпуклый многоугольник Ф расположен целиком в каждой из полуплоскостей, границами которых служат прямые, содержащие каждую из сторон многоугольника. Пересечение всех таких полуплоскостей и дает многоугольник Ф.
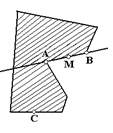
Рис. 1.1.28
Задача №1.1.3
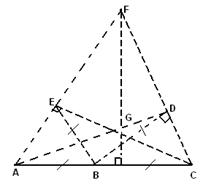
а) Пусть А и В — две внутренние точки фигуры Ф. Согласно определению внутренних точек (определение1.1.4) существуют два круга С и С’ с центрами соответственно в точках А и В, все точки которых принадлежат фигуре Ф (рис. 1.1.29, а). Пусть МN и РQ — внешние общие касательные кругов С и С’. В силу выпуклости Ф вся криволинейная фигура МРQN, заштрихованная на рис. 1.1.29, а) принадлежит Ф, и следовательно, каждая точка D отрезка АВ является центром некоторого круга, все точки которого принадлежат Ф (этот круг вписан в фигуру МРQN).
б) Доказательство почти не отличается от доказательства пункта а), только окружность С’ приходится заменить одной точкой В и фигуру МPQN — фигурой MBN, заштрихованной на рис. 1.1.29, б).
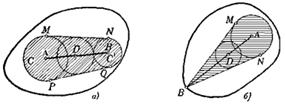
Рис. 1.1.29
в) Пусть А и В — две граничные точки выпуклой фигуры Ф. Отрезок АВ может целиком состоять из граничных точек (рис. 1.1.30, а) — это и есть первый случай, указанный в условии задачи.
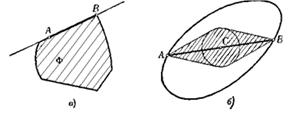
Рис. 1.1.30
Если же какая-либо точка С отрезка АВ является внутренней точкой Ф, то согласно пункту б) все точки отрезков СА и СВ, кроме А и В, должны быть внутренними для Ф — это второй случай, указанный в условии (рис. 1.1.30, б). [8, 140]
Задача №1.1.4
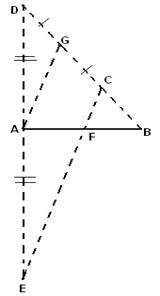
Пусть Ф это выпуклая фигура, О — ее внутренняя точка и l—прямая, проходящая через точку О. Так как прямая l сама является выпуклой фигурой, то ее пересечение с фигурой Ф будет (согласно задаче 1.1.1) выпуклой фигурой, расположенной на прямой (одномерной выпуклой фигурой), т. е. отрезком, лучом или всей прямой. Если это — отрезок, то его концы А и В являются граничными точками фигуры Ф (рис. 1.1.31), и следовательно, прямая l содержит две граничные точки Ф.
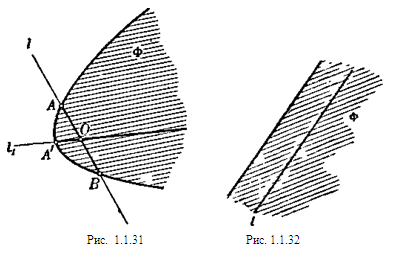
Если это пересечение — луч (прямая l1 на рис. 1.1.31), то его начало А’ будет единственной граничной точкой фигуры Ф, лежащей на прямой l1.
Если, наконец, прямая l целиком принадлежит фигуре (рис. 1.1.32), то на этой прямой нет ни одной граничной точки фигуры Ф.
Если фигура Ф ограничена, то ее пересечение с прямой также ограничено и, следовательно, является отрезком. Таким образом, на каждой прямой l, проведенной через внутреннюю точку ограниченной выпуклой фигуры Ф, имеются ровно две граничные точки этой фигуры. [8, 142]
Задача № 1.1.5
Утверждение данной задачи равносильно утверждению, что для всякой ограниченной невыпуклой фигуры Ф найдется прямая, пересекающая ее границу более чем в двух точках. Докажем это.
Пусть Ф — ограниченная невыпуклая фигура. В таком случае найдутся такие точки А и В, принадлежащие Ф, что отрезок, их соединяющий, не принадлежит целиком фигуре Ф; обозначим через С точку отрезка АВ, не принадлежащую Ф (рис. 1.1.33, а). Мы всегда можем предположить, что точка А — внутренняя точка Ф.
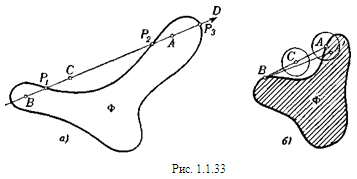
Действительно, если А — граничная точка Ф, А’ — внутренняя точка, достаточно близкая к точке А, то отрезок А’В также будет иметь точки вне фигуры Ф (рис. 1.1.33, б).
Итак, пусть А — внутренняя точка. На отрезке ВС есть граничная точка Р1, фигуры Ф (может быть, совпадающая с В), т.к. точка В принадлежит фигуре Ф, а С лежит вне ее. На отрезке АС также есть граничная точка Р2 фигуры Ф (А лежит внутри Ф, С— вне этой фигуры). Тогда, продолжив отрезок ВА за точку А, мы получим луч АD, исходящий из внутренней точки А фигуры Ф. На этом луче также есть граничная точка Р3 фигуры Ф (т.к. фигура Ф ограничена).
Итак, на прямой АВ, проходящей через внутреннюю точку А фигуры Ф, лежат по крайней мере три граничные точки Р1, Р2 и Р3, что и требовалось доказать. Следовательно, всякая фигура Ф, удовлетворяющая условию задачи, должна быть выпуклой.
Задача №1.1.6
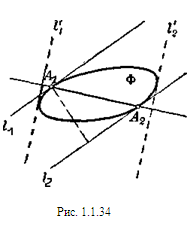
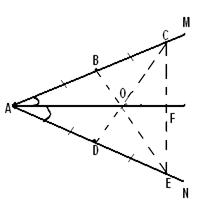
Пусть l1 иl2 — две параллельные опорные прямые фигуры Ф, расстояние между которыми имеет наибольшее значение; А1 и А2 — граничные точки фигуры Ф, принадлежащие соответственно прямым l1 иl2. Покажем, что отрезок А1 А2 перпендикулярен к обеим прямым l1 иl2. В самом деле, если бы это было не так, то расстояние между прямыми l1 иl2 было бы меньше, чем отрезок А1А2 (рис. 1.1.34), и тем более меньше, чем расстояние между двумя опорными прямыми l1’и l2 ’ фигуры Ф, перпендикулярными к отрезку А1А2, что противоречит условию (т.к. мы нашли две опорные прямые расстояние между которыми больше расстояния между опорными прямыми l1 иl2).
Так как А1 и А2 — какие угодно граничные точки фигуры Ф, принадлежащие соответственно прямым l1 иl2, то из перпендикулярности отрезка А1А2 к прямым l1 и l2 следует, что ни одна из прямых l1 и l2 не может иметь с фигурой Ф целый общий отрезок (т. е. случай, изображенный на рис. 1.1.35, невозможен); другими словами, каждая из этих прямых содержит единственную граничную точку фигуры Ф. [8, 143]
Задача №1.1.7
Пусть Ф — выпуклая фигура, l1 и l2 — параллельные опорные прямые, расстояние между которыми имеет наибольшее возможное значение d, А1 и А2 — общие точки фигуры Ф и прямых l1 и l2 соответственно. Так как отрезок А1А2 перпендикулярен к прямым l1 и l2 (см. задачу 1.1.6), то длина его равна d (рис. 1.1.36). Остается только доказать, что расстояние между любыми двумя точками фигуры Ф не превосходит d. Действительно, если В и С — какие-либо две точки фигуры Ф, а т и п — опорные прямые, перпендикулярные к прямой содержащей отрезок ВС (рис. 1.1.37), то отрезок ВС не превосходит расстояния между прямыми т и п, которое в свою очередь не превосходит d. Следовательно, длина ВС не может быть больше d.
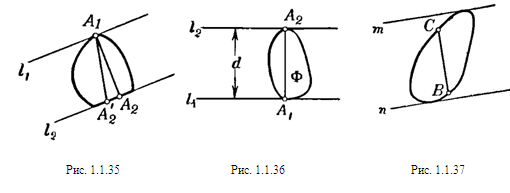
Задача №1.1.8
Проведем две опорные прямые l и т выпуклой фигуры Ф, перпендикулярные к отрезку АВ. Вся фигура Ф заключена в полосе между прямыми l и т, а следовательно, в этой полосе помещается и отрезок АВ длины d, перпендикулярный к прямым l и т. Но так как расстояние между прямыми l и т не может быть больше d (задача 1.1.7), то прямые l и т должны проходить через концы А и В отрезка. [8, 145]
Похожие работы
... дроби, использовать знания по оперированию единицами величины, при решении задач. развивающие: развивать логическое мышление, память, внимание, умение оперировать обыкновенными дробями. воспитательные: воспитывать любовь к математике, дисциплинированность, самостоятельность, аккуратность. Ход урока. I. Организация класса - Здравствуйте, ребята! Приготовитесь к уроку. ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
... – педагогический эксперимент. Эксперимент проходил в три этапа: 1 этап – констатирующий эксперимент. При его проведении были выявлены знания учащихся по теме «Использование и измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии», при этом использовались различные формы и методы выявления знаний, такие как: анкетирование, беседы с учащимися и учителями, ...
... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...





0 комментариев