Навигация
Отыскание оптимального пятиугольника
92071
знак
0
таблиц
61
изображение
2. Отыскание оптимального пятиугольника
Теорема 2.2.1. Оптимальным пятиугольником является правильный пятиугольник.
Доказательство.
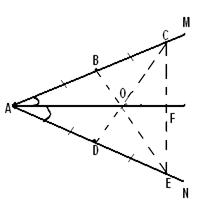
Рассмотрим пятиугольник MPFTN у которого четыре диагонали равны 1 (по теореме 2.1.4 только такой пятиугольник может быть оптимальным).
Пусть
PN=MT=FM=FN=1, PT=c (рис. 2.2.1).
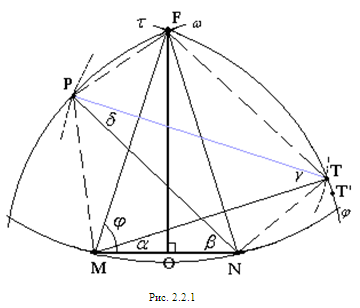
Положим
FMN=FNM=
, TMN=
, PNM=
, NPT=
, PTM=
, FO 
MN.
Найдем периметр p пятиугольника MPFTN.
Из 
FMO:
MO= cos, MN=2 cos.
Из треугольников NPF и MFT имеем:
PF=
,
FT=
.
Из треугольника РМТ и ТNР по теореме косинусов имеем:
PM=
,
ТN=
.
Таким образом периметр р пятиугольника MPFTN равен:
р=2cos+++
+
.
Рассмотрим сначала случай, когда с=1, т.е. все диагонали пятиугольника MPFTN равны 1.
В этом случае:
p=2 cos++++=
=2 cos+++2sin
+2sin
=
=2cos +4 sin
+4sin
2cos +4 sin
+4sin
=2cos +4 sin
+4sin=
=2cos +8sin
cos
2cos+8sin , (т.к. 
).
Исследуем функцию
g ()= 2cos+8sin.
g’()= (2cos+8sin)’= - 2sin+2cos=
.
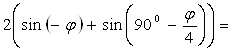
Так как
2cos<1 , то cos<
, >60
.
Значит 60<<90, и мы получаем, что 67,5 <
+45<78,75 .
Последнее неравенство означает, что (+45) - угол первой четверти, т.е. cos(+45)>0.
sin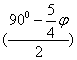
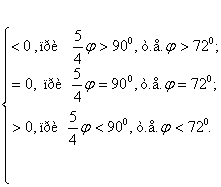
Поэтому
p2cos+8sin 2cos72+8sin18
Таким образом, в случае с=1 периметр пятиугольника не превосходит периметра правильного пятиугольника.
Рассмотрим теперь случай, когда с<1.
Проведем эллипсы через точки Р и Т с фокусами соответственно в точках F, M и F, N. Пусть хотя бы один эллипс пересекает соответствующую дугу 
или
(рис. 2.2.1). Пусть, например, эллипс проведенный через точку Т пересекает дугу . Тогда сместив вершину Т в близкую точку Т’ дуги FT, мы получим пятиугольник большего периметра.
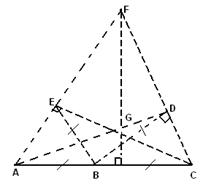
Остается, следовательно, проверить случай, когда оба эллипса касаются соответствующих дуг. Но из геометрических соображений ясно, что существует не более одной точки дуги , в которой соответствующий эллипс касается этой дуги (рис. 2.2.2). Тем же свойством обладает симметричная точка дуги . Поэтому, если оба эллипса касаются соответствующих дуг, то 
. Оценим периметр пятиугольника в этом случае.
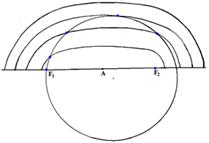
Рис. 2.2.2
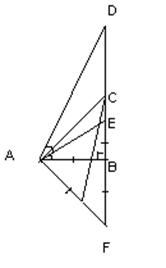
Заметим сначала (рис. 2.2.3), что в виду имеем, что PT||MN , откуда 
и 
. Проведем NT’ || MT, тогда
c=PT=PT’-TT’=PT’-MN=2cos-2cos.
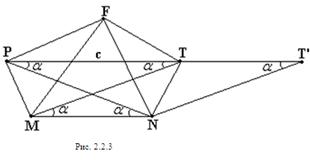
Из 
MPT:
PM
=
= (2cos-2cos) +1-2(2cos-2cos) cos=
=
=
= 1- 2c cos , то есть
PM=
=NT.
Тогда периметр p пятиугольника MPFTN равен:
p=2+4sin
.
Докажем неравенство
.
Имеем:
1-2c cos -4sin
=1-2c cos-2(1-cos)=1-2c cos-2(1-(
))=
=1-2c cos-2+c+2cos=-1+c+2cos(1-c)=( 1- c)(-1+2cos)<0,
т.к. c<1, (1- c)>0 и 2cos-1<0, >60.
Таким образом:
1-2ccos <4sin т.е. .
Отсюда имеем:
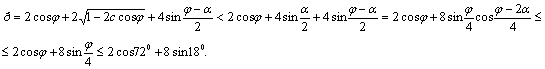
Иначе говоря, периметр пятиугольника MPFTN в этом случае меньше периметра правильного пятиугольника.
Таким образом, оптимальным пятиугольником является правильный пятиугольник.
Теорема доказана.
Заключение
Экстремальные задачи — задачи на максимум и минимум — во все времена привлекали внимание учёных. Причина такого интереса заключается, во-первых, в том, что многие экстремальные задачи приходят из практики. Леонард Эйлер (1707-1783), один из величайших математиков, говорил: "В мире не происходит ничего, в чём бы не был виден смысл какого-нибудь максимума или минимума". Во-вторых, среди задач на максимум и минимум много красивых задач, которые интересно и полезно решать.
В данной работе рассмотрены различные планиметрические задачи на максимум и минимум, а также изложены основные теоретические сведения, необходимые для решения экстремальных задач. Основное внимание в работе было уделено решению весьма не тривиальной задачи на максимум, а именно отысканию пятиугольника заданного диаметра, имеющего наибольший периметр. При решении поставленной задачи были использованы как геометрические, так и аналитические методы и доказана основная теорема о том, что в пятиугольнике наибольшего периметра по крайней мере четыре диагонали равны единице. В заключительной теореме показано, уже чисто аналитически, что искомым является правильный пятиугольник.
Таким образом, основная цель работы достигнута.
Библиография
1. Болтянский, В.Г. Теоремы и задачи комбинаторной геометрии [Текст]/ В.Г. Болтянский, И.Ц. Гохберг.- М.: НАУКА, 1965.- 108 с.: ил.
2. Математика, ее преподавание, приложения и история [Электронный документ]/ Я.С. Дубнов, В.Г. Болтянский, В.А. Ефремович и др.; Под ред. Я.С. Дубнов.- вып.3.- М.: Физ.– мат. лит., 1958.- 321 с.
3. Протасов, В.Ю. Максимумы и минимумы в геометрии [Текст]/ В.Ю. Протасов.- М.: НЦНМО, 2005.- 56 с.
4. Тихомиров, В.М. Рассказы о максимумах и минимумах [Текст]/ Тихомиров В.М.- М.: НАУКА, 1986.- 192 с.
5. Трофимов, В.В. Царевна Дидона, изопериметры и мыльные пленки [Электронный документ]
(http://mirror1.mccme.ru/kvant/1985/05/carevna_didona_izoperimetry_i.htm)
6. Шклярский, Д.О. Геометрические оценки и задачи из комбинаторной геометрии [Текст]/ Д.О. Шклярский, И.М. Яглом, Н.Н. Ченцов.- М.: НАУКА , 1974.- 384 с.: ил.
7. Энциклопедия элементарной математики [Текст]/ В.Г. Болтянский, В.А. Рохлин, И.М. Яглом, Б.А. Розенфельд и д.р.; Под ред. В.Г. Болтянский.- книга 5.- М.: Физ.– мат. лит., 1966.- 624 с.: ил.
8. Яглом, И.М. Выпуклые фигуры [Текст]/ И.М. Яглом, В.Г. Болтянский.- М.Л.: Гос. изд-во технико-теоретической лит., 1951.- 343 с.
Похожие работы
... дроби, использовать знания по оперированию единицами величины, при решении задач. развивающие: развивать логическое мышление, память, внимание, умение оперировать обыкновенными дробями. воспитательные: воспитывать любовь к математике, дисциплинированность, самостоятельность, аккуратность. Ход урока. I. Организация класса - Здравствуйте, ребята! Приготовитесь к уроку. ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
... – педагогический эксперимент. Эксперимент проходил в три этапа: 1 этап – констатирующий эксперимент. При его проведении были выявлены знания учащихся по теме «Использование и измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии», при этом использовались различные формы и методы выявления знаний, такие как: анкетирование, беседы с учащимися и учителями, ...
... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...
0 комментариев