Задачи

3.1 Задачи

Задача №1.3.1. Докажите, что плоская фигура Ф не может иметь двух различных описанных окружностей. Докажите также, что описанная окружность плоской фигуры Ф обязательно содержит или две граничные точки Ф, являющиеся диаметрально противоположными точками окружности, или же три граничные точки Ф, являющиеся вершинами остроугольного треугольника. Выведите отсюда, что радиус R описанной окружности плоской фигуры Ф диаметра 1 заключается в границах:

0,5 £ R £ = 0,577… [7, 201]

Задача №1.3.2. Докажите, что вписанная окружность выпуклой фигуры Ф обязательно содержит или две граничные точки Ф, являющиеся диаметрально противоположными точками окружности, или три граничные точки Ф, являющиеся вершинами остроугольного треугольника; в последнем случае вписанная окружность Ф является единственной. Докажите также, что радиус r вписанной окружности выпуклой фигуры Ф ширины 1 заключается в границах:

 £ r £. [8, 76]

Задача №1.3.3. Докажите, что из всех выпуклых кривых ширины 1 наименьшую площадь ограничивает равносторонний треугольник с высотой 1.

Задача №1.3.4. Докажите, что треугольник имеет меньшую площадь, чем каждая другая выпуклая фигура того же самого диаметра и той же самой ширины. [8, 80]

3.2 Решения

Задача №1.3.1

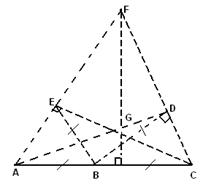
Фигура Ф не может иметь двух различных описанных окружностей, потому что если бы Ф содержалась внутри двух окружностей S и S’ одного и того же радиуса R, то она заключалась бы также внутри заштрихованного на рис. 1.3.7 двуугольника, образованного пересечением окружностей S и S’, а следовательно, и внутри окружности, описанной вокруг этого двуугольника (изображенной пунктиром на рис. 1.3.7).

Но последняя окружность имеет меньший радиус, чем окружности S и S’, что противоречит тому, что окружности S и S’ — описанные окружности фигуры Ф. Далее, если окружность S, заключающая плоскую фигуру Ф внутри себя, вообще не содержит граничных точек Ф, то существует окружность меньшего радиуса, также содержащая Ф внутри себя.

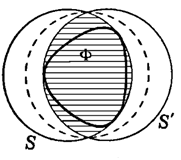
Рис. 1.3.7

Чтобы получить эту окружность, будем постепенно уменьшать радиус окружности S, не меняя ее центра, до тех пор, пока уменьшенная окружность не коснется границы фигуры Ф в какой-либо точке А (рис. 1.3.8, а). [8, 246]

Рис. 1.3.8

Если окружность S, заключающая фигуру Ф внутри себя, содержит единственную граничную точку А фигуры Ф, то также существует окружность S’ меньшего радиуса, заключающая Ф внутри себя. Для того чтобы это доказать, сдвинем окружность S в направлении радиуса ОА (О — центр окружности S) так, чтобы точка А оказалась внутри окружности (рис. 1.3.8, б). При этом мы получим окружность того же радиуса, что и S, заключающую фигуру Ф внутри себя и не содержащую граничных точек Ф; согласно вышесказанному радиус этой окружности можно уменьшить так, чтобы она все еще содержала фигуру Ф внутри себя.

Наконец, если окружность S, заключающая фигуру Ф внутри себя, содержит две граничные точки А и В фигуры Ф, не являющиеся диаметрально противоположными точками S, и дуга окружности S, большая полуокружности, с концами в точках A и B не содержит более никаких точек Ф, то также существует окружность, радиус которой меньше радиуса S и которая заключает фигуру внутри себя. Для доказательства сдвинем несколько окружность S в направлении, перпендикулярном к хорде АВ так, чтобы точки А и В оказались внутри окружности (рис. 1.3.8, в). При этом мы снова получим окружность того же радиуса, что и S, содержащую Ф внутри себя и не содержащую граничных точек Ф; радиус этой окружности можно уменьшить так, чтобы Ф все еще оставалась внутри окружности.

Таким образом, наименьшая из содержащих Ф окружностей обязательно должна содержать либо две точки Ф, являющиеся диаметрально противоположными точками окружности (рис. 1.3.9, а), либо три такие точки Ф, что никакая из дуг окружности между какими-либо двумя из этих трех точек не больше полуокружности (т.е. три точки, являющиеся вершинами остроугольного треугольника; рис. 1.3.9, б). [6, 301]

Рис. 1.3.9

Отсюда сразу следует, что радиус R описанной окружности S фигуры Ф диаметра 1 заключается в указанных в условии задачи границах. Действительно, прежде всего, так как фигура Ф заключается внутри окружности S радиуса R, наибольшее расстояние между точками которой равно 2R, то из того, что диаметр Ф равен 1, сразу следует, что 2R1, R. Таким образом, остается только доказать, что R. [8, 248]

Если описанная окружность содержит две точки Ф, являющиеся диаметрально противоположными точками окружности, то, так как расстояние между этими точками не больше 1, радиус R окружности не может быть больше , следовательно, он равен  и, значит, меньше. Если же описанная окружность S фигуры Ф содержит три точки Ф, являющиеся вершинами остроугольного треугольника АВС, то по крайней мере один из углов а этого остроугольного треугольника не меньше 60°. Синус этого угла не меньше, и так как сторона а, противолежащая этому углу, не больше 1, то диаметр 2R окружности S, описанной вокруг треугольника АВС, равный не больше .

Отсюда получаем, что

R=. [6, 302]

Задача №1.3.2

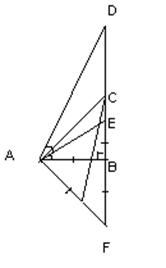
Решение очень похоже на предыдущее. Прежде всего, если окружность S, целиком заключающаяся внутри выпуклой фигуры Ф, не содержит совсем граничных точек Ф, то существует заключающаяся внутри Ф окружность S’, радиус которой больше радиуса S. Чтобы найти эту окружность, будем постепенно увеличивать радиус S, не меняя ее центра, до тех пор, пока увеличенная окружность не коснется границы Ф в какой-либо точке А (рис. 1.3.10, а).

Если окружность S, заключающаяся целиком внутри выпуклой фигуры Ф, содержит единственную граничную точку А фигуры Ф, то тоже существует окружность, радиус которой больше радиуса S, заключающаяся внутри Ф. Для того чтобы это доказать, сдвинем несколько окружность S в направлении радиуса АО (О — центр окружности S) так, чтобы точка А оказалась вне окружности (рис. 1.3.10, б). При этом мы получим окружность того же радиуса, что и S, заключенную внутри Ф и не имеющую с границей Ф общих точек; согласно вышесказанному, радиус этой окружности можно увеличить так, чтобы она все еще оставалась заключенной внутри Ф. Наконец, если окружность S, заключенная внутри фигуры Ф, содержит две такие граничные точки А и В фигуры Ф, что дуга АВ окружности S, большая 180°, не содержит никаких других граничных точек Ф, то также существует окружность большего радиуса, чем S, содержащаяся целиком внутри Ф. Действительно, сдвинем окружность S в направлении, перпендикулярном к хорде АВ так, чтобы точки А и В оказались вне окружности (рис. 1.3.10, в). При этом мы получим окружность того же радиуса, что и S, заключающуюся внутри Ф и не имеющую с границей Ф общих точек; радиус этой окружности мы можем увеличить так, чтобы она все еще оставалась внутри Ф.

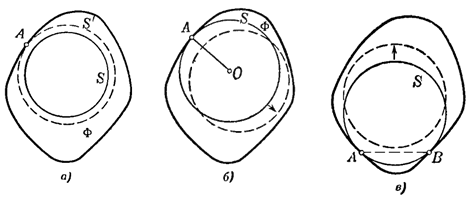
Рис. 1.3.10

Таким образом, наибольшая из всех содержащихся в Ф окружностей должна содержать либо две граничные точки Ф, являющиеся диаметрально противоположными точками окружности (рис. 1.3.11, а), либо три такие граничные точки Ф, что никакая из дуг окружности между какими-либо двумя из этих трех точек не больше полуокружности, т. е. три точки, являющиеся вершинами остроугольного треугольника (рис. 1.3.11, б). [8, 249]

Отсюда нетрудно вывести, что радиус r вписанной окружности выпуклой фигуры Ф ширины 1 заключается в указанных в условии задачи пределах. Прежде всего, так как окружность S заключается внутри Ф, а следовательно, и внутри каждой полосы, образованной парой параллельных опорных прямых фигуры Ф, то диаметр S не может быть больше 1 и, следовательно, радиус r окружности S не может быть больше . Таким образом, требуется доказать только, что r не может быть меньше  .

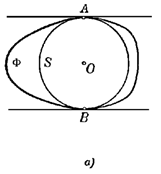
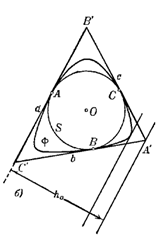
Рис 1.3.11

Если вписанная в выпуклую фигуру Ф окружность S соприкасается с границей Ф в точке А, то опорная прямая фигуры Ф, проходящая через точку А, должна быть одновременно и опорной прямой окружности S. Но так как через граничную точку окружности можно провести только единственную опорную прямую, то отсюда следует, что фигура Ф может иметь в точке А единственную опорную прямую, совпадающую с касательной к окружности S (т. е. точка А не может быть угловой точкой фигуры Ф). Отсюда прежде всего вытекает, что если вписанная в Ф окружность S содержит две граничные точки А и В фигуры Ф, являющиеся диаметрально противоположными точками S, то радиус S равен половине расстояния между параллельными опорными прямыми фигуры Ф, проведенными в точках А и В, и не может быть меньше, следовательно, в этом случае обязательно r = (рис. 1.3.11, а).

Если же вписанная окружность S фигуры Ф содержит три граничные точки А, В, С фигуры Ф, являющиеся вершинами остроугольного треугольника, то опорные прямые фигуры Ф, проведенные в точках А, В, С, образуют некоторый треугольник А’В’С’, описанный одновременно вокруг Ф и вокруг окружности S (рис. 1.3.11, б). Обозначим стороны этого треугольника через а, b, с (а — наибольшая сторона), а соответствующие высоты — через h_a, h_b,h_c.

Площадь треугольника А’В’С’ равна, с одной стороны, r, а с другой, .

Так как, а b, а с, то из равенства:

r =

следует:

h_a=  r  3r,

r.

Но высота  треугольника А’В’С’, описанного вокруг фигуры Ф, не может быть меньше ширины Ф (см. рис. 1.3.11, б); отсюда следует, что r , что и требовалось доказать.

В том случае, когда вписанная в выпуклую фигуру Ф окружность S содержит три граничные точки Ф, являющиеся вершинами остроугольного треугольника, существует треугольник А’В’С’, описанный одновременно вокруг Ф и вокруг S. Отсюда следует, что в этом случае вписанная окружность S является единственной — всякая другая окружность, содержащаяся внутри Ф, должна также содержаться внутри треугольника А’В’С’ и, следовательно, будет меньше, чем окружность S, вписанная в треугольник А’В’С’. Однако, если вписанная окружность соприкасается с границей Ф в двух диаметрально противоположных точках, то она может быть и не единственной (см. рис. 1.3.1). [8, 250]

Задача №1.3.3

Прежде всего отметим, что в силу результата задачи 1.3.2 радиус r круга S, вписанного в фигуру Ф ширины 1, не больше  и не меньше . При этом если r = , то площадь фигуры Ф не меньше =0,78..., что больше площади равностороннего треугольника высоты 1, равной = 0,57... Если же r = , то Ф есть равносторонний треугольник высоты 1.

Пусть теперь радиус вписанного круга S фигуры Ф равен r (r<) тогда существует треугольник Т, описанный одновременно вокруг Ф и вокруг S (см. решение задачи 1.3.2, рис. 1.3.11, б). Проведем еще три опорные прямые фигуры Ф, соответственно параллельные сторонам треугольника Т; точки соприкосновении этих опорных прямых с границей фигуры Ф (какие-нибудь из точек соприкосновения, если эти прямые содержат целые отрезки, принадлежащие границе Ф) обозначим через А’, В’, С’ (рис. 1.3.12). Центр круга S обозначим через О. Так как расстояние между парой параллельных опорных прямых фигуры Ф не может быть меньше 1, а точка О отстоит от каждой из сторон треугольника на расстояние r, то расстояние от точек А’, В’, С’ до точки О не меньше 1 — r. На отрезках ОА’, ОВ’, ОС’ отметим точки А, В, С, удаленные от О на расстояние 1 — r. Проведя из точек А, В, С касательные к кругу S, мы получим фигуру Ф_r, состоящую из круга радиуса r и трех равных между собой частей, ограниченных кругом и двумя касательными круга (см. рис. 1.3.12); эта фигура заключается внутри нашей фигуры Ф. Если r =, то Ф_r = Ф представляет собой равносторонний треугольник с высотой 1. [8, 256]

Достаточно доказать, что из всех фигур Ф_r (r<) соответствующих разным значениям r наименьшую площадь имеет равносторонний треугольник Ф.

На рис. 1.3.13 изображены равносторонний треугольник РQR и фигура Ф_r(<r<).

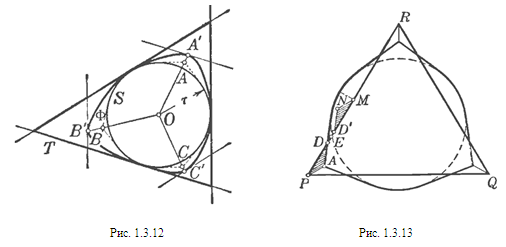
Нетрудно видеть, что общая площадь частей равностороннего треугольника, выходящих за пределы фигуры Ф_r, меньше площади частей фигуры Ф_r расположенных вне треугольника Ф. Части треугольника, расположенные вне Ф_r, состоят из шести треугольников таких, как треугольник АPD, заштрихованный на рис. 1.3.13. Пусть М — середина стороны РR треугольника РQR. Проведем из точки М отрезок МN, равный и параллельный РА. Точка N будет находиться внутри круга, составляющего часть фигуры Ф_r, так как наименьшее расстояние от точки М до окружности (расстояние по перпендикуляру к РR) равно, как нетрудно видеть, РА (это можно вывести из того, что наибольшее расстояние от точки А до окружности равно 1, как и высота треугольника). Соединим N с А; пусть NА пересекает РR в точке Е.

Треугольник МNЕ равен треугольнику ЕАР, а треугольник DАР составляет лишь часть ЕАР. Таким образом, мы можем перенести треугольник DАР внутрь МNЕ, т. е. внутрь Ф_r (новое положение треугольника DАР тоже заштриховано на рис. 1.3.13). Перенеся таким же образом все шесть треугольников, таких, как DАР, внутрь Ф_r, мы убедимся, что равносторонний треугольник Ф имеет меньшую площадь, чем фигура Ф_r. Этим и завершается доказательство. [8, 257]

Задача №1.3.4

Пусть Ф— некоторая выпуклая фигура диаметра D и ширины . Докажем, что площадь Ф не может быть меньше площади треугольника с основанием D и высотой , т. е. не может быть меньше  D.

Пусть А и В — две граничные точки фигуры Ф, расстояние между которыми является наибольшим (равно D). Через точки А и В проведем опорные прямые l₁ и l₂ фигуры Ф, перпендикулярные к отрезку АВ; проведем также две другие опорные прямые m₁ и m₂ фигуры Ф, перпендикулярные к l₁ и l₂ (параллельные АВ; рис. 1.3.14, а). Согласно определению ширины выпуклой фигуры, расстояние между прямыми m₁ и т₂ не может быть меньше; следовательно, площадь прямоугольника PQRS образованного прямыми l₁, m₁,l₂ и т₂ не может быть меньше D.

Пусть С — точка соприкосновения опорной прямой m₁ (стороны РS прямоугольника PQRS) с фигурой Ф, Е— точка соприкосновения прямой т₂ с фигурой Ф. В силу выпуклости фигуры Ф она должна содержать целиком четырехугольник ВСАЕ. Но площадь треугольника AВС равна половине площади прямоугольника АВSР; площадь треугольника АВЕ равна половине площади прямоугольника АQRВ. Таким образом, площадь ВСАЕ равна половине площади прямоугольника PQRS и, следовательно, не может быть меньше D; следовательно, и площадь Ф не может быть меньше  D.

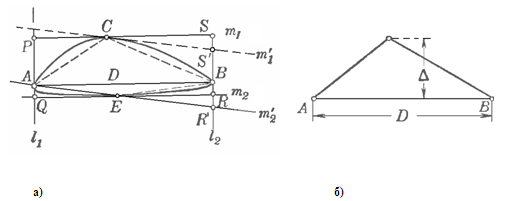
Рис. 1.3.14

Из приведенного решения нетрудно увидеть, что площадь Ф равна D только в том случае, когда фигура Ф есть треугольник. Действительно, прежде всего фигура Ф площади D должна совпадать с четырехугольником ВСАЕ (см. рис. 1.3.14, а), причем диагональ АВ должна быть равна диаметру D четырехугольника BСAЕ, а расстояние между прямыми m₁ и т₂ ширине . Но последнее возможно только в том случае, когда отрезок АВ совпадает с одной из сторон РS или QR прямоугольника PQRS. Действительно, в противном случае через точки С и Е всегда возможно провести опорные прямые m₁’и т₂’ четырехугольника ВСАЕ, расстояние между которыми будет меньше расстояния между m₁ и т₂ (см. рис. 1.3.14, а; если СSЕR, то SS’ RR’, SRS’R’ и, следовательно, расстояние между m₁’и т₂’ и подавно меньше SR). [8, 266]

Таким образом, площадь выпуклой фигуры может быть равна D только в том случае, когда Ф есть треугольник с основанием D и высотой  (рис. 1.3.14, б). [8, 265]

Глава 2. Оценка периметра пятиугольника единичного диаметра

Похожие работы

Дроби

Скачать

78083

7

3

... дроби, использовать знания по оперированию единицами величины, при решении задач. развивающие: развивать логическое мышление, память, внимание, умение оперировать обыкновенными дробями. воспитательные: воспитывать любовь к математике, дисциплинированность, самостоятельность, аккуратность. Ход урока. I. Организация класса - Здравствуйте, ребята! Приготовитесь к уроку. ...

Развитие логического мышления учащихся при решении задач на построение

Скачать

249522

15

58

... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...

Использование измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии

Скачать

79870

10

43

... – педагогический эксперимент. Эксперимент проходил в три этапа: 1 этап – констатирующий эксперимент. При его проведении были выявлены знания учащихся по теме «Использование и измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии», при этом использовались различные формы и методы выявления знаний, такие как: анкетирование, беседы с учащимися и учителями, ...

Психолого-педагогическое обоснование внеклассной работы по математике

Скачать

113174

0

0

... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...