Навигация
Доказательство равенства четырех диагоналей пятиугольника единице
92071
знак
0
таблиц
61
изображение
1. Доказательство равенства четырех диагоналей пятиугольника единице
Определение 2.1.1. Диаметром d многоугольника М называется точная верхняя граница расстояний между его точками. [6, 68]
d=sup
(X,Y)
Х
M, УM
Теорема 2.1.1. Диаметр многоугольника равен расстоянию между некоторыми его вершинами.
Доказательство.
Многоугольник М является ограниченной замкнутой областью. По теореме Вейерштрасса непрерывная функция (X,Y) достигает своего максимума в этой области. Иными словами существуют такие две точки А и В многоугольника, что:
(А, В) = sup (X, Y) = d.
ХM, УM
Отрезок АВ также будем называть диаметром многоугольника.
Ясно, что концы диаметра многоугольника должны находиться на его границе, при этом если хотя бы один из концов диаметра АВ не является вершиной многоугольника, то как видно из рисунка 2.1.1, один из отрезков K1B, K2B будет больше АВ (т.к. один из углов 
K1АB, K2АB не является острым), что невозможно.
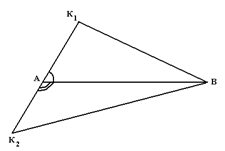
Рис. 2.1.1
Теорема доказана.
Итак, диаметр многоугольника совпадает либо с одной из сторон, либо с одной из диагоналей многоугольника.
Определение 2.1.2. Выпуклый многоугольник диаметра 1 будем называть оптимальным, если его периметр больше периметра любого другого выпуклого многоугольника диаметра 1.
Теорема 2.1.2. Все стороны оптимального пятиугольника меньше 1.
Для доказательства теоремы потребуется следующая лемма.
Лемма 2.1.1. Сумма расстояний от точки дуги окружности до ее концов принимает наибольшее значение, когда эта точка делит дугу пополам.
Доказательство.
Пусть Р – точка дуги окружности, точки F и M ее концы (рис. 2.1.2).
Из 
FPО и PОM получаем:
FP+PM=2 r sin
+ 2 r sin
=2 r (sin+sin ) =
=2 r (2sin
cos
),
здесь
и по симметрии можно считать, что
, т.е. 
.
Сумма FP+PMпринимает наибольшее значение, когда cos=1.
Так как
<
, то 
,
а это значит, что
= 
.
Лемма доказана.
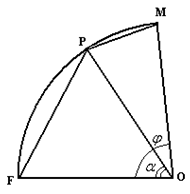
Рис. 2.1.2
Доказательство теоремы.
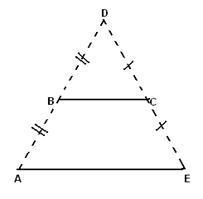
Пусть сторона FT рассматриваемого пятиугольника FPMNT равна 1. Для доказательства проверим, что периметр р пятиугольника FPMNT меньше периметра правильного пятиугольника диаметра 1.
Проведем две окружности:
с центром в точке T радиуса FT;
и 
с центром в точке F радиуса FT.
Очевидно, что остальные вершины пятиугольника будут лежать в области ограниченной окружностями и и в одной полуплоскости относительно стороны FT (в силу выпуклости пятиугольника) (рис. 2.1.3).
Возможны два случая расположения вершин P, M, N пятиугольника FPMNT.
Рассмотрим первый случай, когда хотя бы одна из прямых РМ и MN пересекает дуги обеих окружностей , .
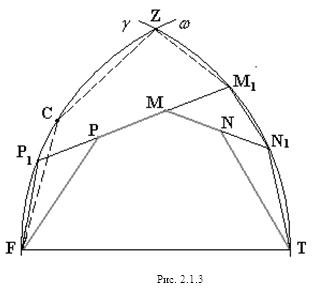
Из рисунка 2.1.3 видно, что периметр p рассматриваемого пятиугольника FPMNT меньше периметра пятиугольника FP1М1N1T, а так же меньше периметра Р1 шестиугольника FСZМ1N1T, где C середина дуги 
(по лемме 2.1.1).
Таким образом, получаем: p< Р1 <4 sin150+1+
3,0819428.
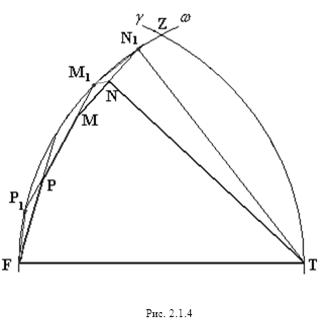
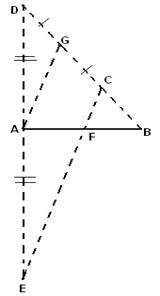
Рассмотрим второй случай, когда прямые PM, MN пересекают дугу окружности (рис. 2.1.4).
Из рисунка 2.1.4 видно, что периметр p рассматриваемого пятиугольника FPMNT меньше периметра P2 пятиугольника FP1М1N1T т.е.:
p< P 2 <+1+13,0466.
Известно, что периметр P3 правильного пятиугольника равен:
P3= 
.
Таким образом, получаем, что периметр рассматриваемого пятиугольника FPMNT меньше периметра правильного пятиугольника диаметра 1.
Теорема доказана.
Теорема 2.1.3. В оптимальном пятиугольнике, по крайней мере, три диагонали равны 1.
Доказательство.
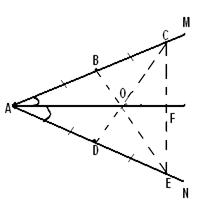
Пусть диагональ PT=1 (по теореме 2.1.2).
Проведем две окружности: (T, PT=1) и (P, PT=1) (рис. 2.1.5). Ясно, что все остальные вершины пятиугольника будут являться внутренними или граничными точками области ограниченной окружностями , и прямой РТ. Причем все три вершины не могут лежать по одну сторону от PT, т.к. PT это диагональ выпуклого пятиугольника (рис. 2.1.5).
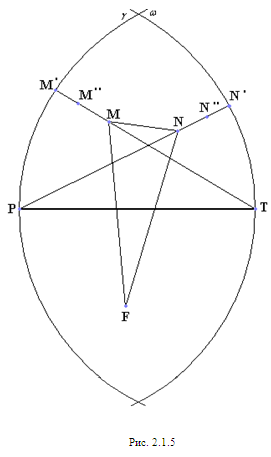
Рассмотрим первый случай, когда прямая MN пересекает дуги обеих окружностей и (рис. 2.1.5).
Допустим, что диагональ FM<1 и точка М отлична от точки M’, тогда сместив точку М в близкую точку М’’ вдоль прямой ТМ’, получим пятиугольник большего периметра, т.е. пятиугольник FPMNT не является оптимальным. Можно поэтому считать, что у оптимального пятиугольника хотя бы одна из диагоналей FM, ТM’ равна 1.
Аналогично, хотя бы одна из диагоналей FN, PN’ равна 1.
Точно так же рассматривается второй случай, когда прямая MN пересекает только одну из окружностей , (рис. 2.1.6).
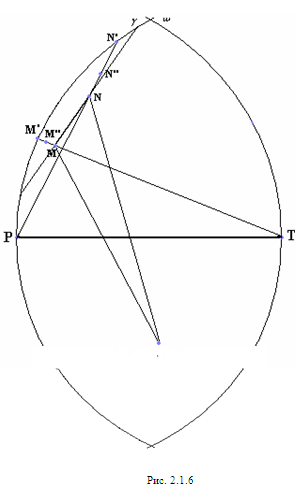
Теорема доказана.
Теорема 2.1.4. В оптимальном пятиугольнике, по крайней мере, четыре диагонали равны 1.
Доказательство.
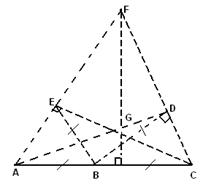
В силу теоремы 2.1.3 рассмотрим пятиугольник MNTFP у которого три диагонали равны единице, при этом возможны два случая:
1) TP= MF=NF=1;
2) TP= MT=NP=1 (рис. 2.1.7).
Рассмотрим первый случай.
Проведем три окружности:
окружность с центром в точке N и радиуса NF=1;
окружность с центром в точке M и радиуса MF=1;
окружность 
с центром в точке F и радиуса FM=FN=1.
Обозначим точки пересечения окружностей и через L, а окружностей и через K (рис. 2.1.7).
Ясно, что вершины P и T пятиугольника с одной стороны будут лежать вне треугольника MNF, т.к. пятиугольник выпуклый, а с другой стороны должны лежать в области ограниченной окружностями , и (область закрашенная на рисунке 2.1.7), т.к. в противном случае, например, если точка Т будет лежать вне этой области, то диагональ МТ >1, а это невозможно т.к. диаметр пятиугольника равен 1. При этом точка P не может лежать на дуге 
MK , а точка Т не может лежать на дуге NL, так как в противном случае мы получим, что сторона пятиугольника равна 1, что невозможно по теореме 2.1.2.
Допустим от противного, что NP<1 и MT<1.
Проведем два эллипса:
l1 с фокусами M, F , проходящий через точку P;
l2 с фокусами N, F , проходящий через точку T.
Возможны два случая:
а) касательные m
в точке P и m
в точке T к эллипсам l1 иl2 соответственно перпендикулярны отрезку PT (рис. 2.1.7).
Подвинем отрезок PТ параллельно самому себе на небольшое расстояние, так, что бы новый отрезок P’Т’ (P’m, Т’m) остался в закрашенной области (или на границе) (рис. 2.1.7).
В результате, длина отрезка PТ не изменится, а длина диагоналей NP’и MT’ не станет больше 1. При этом периметр пятиугольника MP’FT’N больше периметра исходного пятиугольника MPFTN.
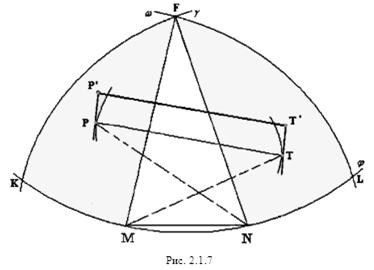
Значит, пятиугольник MPFTN не может быть оптимальным.
б) Одна из касательных m в точке P или m в точке T к эллипсам l1 иl2 соответственно не перпендикулярна отрезку PT.
Допустим, что касательная m в точке P к эллипсу l1 не перпендикулярна отрезку PT. Проведем окружность 
с центром в точке T и радиусом PT=1 (рис. 2.1.8).
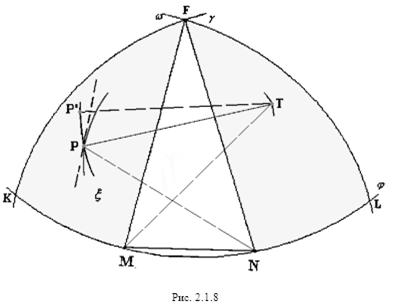
Подвинем точку P по дуге окружности , которая "выходит" из эллипса l1 и получим точку P’. При этом длина PT не изменится, а точку P мы подвинем на такое расстояние, что бы точка P’ лежала в закрашенной области. А это значит, что диагональ NP’ не станет больше 1. Периметр полученного таким образом пятиугольника MP’FTN больше периметра исходного пятиугольника MPFTN.
Значит, пятиугольник MPFTN не может быть оптимальным.
Таким образом, в оптимальном пятиугольнике, покрасней мере одна из диагоналей NP, MT равна единице.
Теперь рассмотрим второй случай.
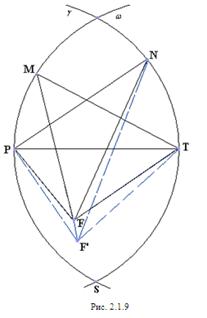
2) TP= MT= NP=1 (рис. 2.1.9).
Заметим, что вершина F лежит внутри области ограниченной отрезком РТ и дугами PS и ST.
Предположив, что NF<1 и MF<1 и заменив точку F близкой точкой F’ (см. рис. 2.1.9), мы получим, что РF+FТ<PF’+F’T, т.е. периметр пятиугольника MPF’TN больше периметра исходного пятиугольника MPFTN.
Значит, пятиугольник MPFTN не может быть оптимальным.
Таким образом, в оптимальном пятиугольнике, покрасней мере одна из диагоналей NF, MF равна единице.
Теорема доказана.
Похожие работы
... дроби, использовать знания по оперированию единицами величины, при решении задач. развивающие: развивать логическое мышление, память, внимание, умение оперировать обыкновенными дробями. воспитательные: воспитывать любовь к математике, дисциплинированность, самостоятельность, аккуратность. Ход урока. I. Организация класса - Здравствуйте, ребята! Приготовитесь к уроку. ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
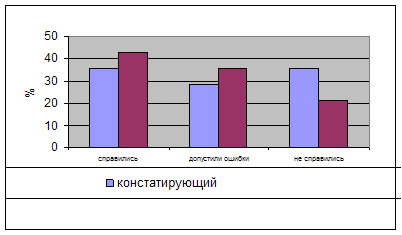
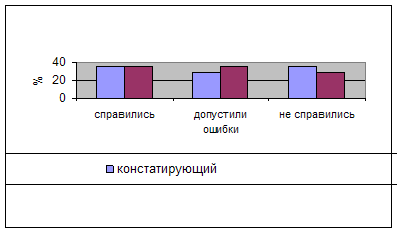
... – педагогический эксперимент. Эксперимент проходил в три этапа: 1 этап – констатирующий эксперимент. При его проведении были выявлены знания учащихся по теме «Использование и измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии», при этом использовались различные формы и методы выявления знаний, такие как: анкетирование, беседы с учащимися и учителями, ...
... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...
0 комментариев