Лекция. Сызықты көптік корреляция

5 Лекция. Сызықты көптік корреляция.

Корреляция коэффиценті эконометрикалық үлгідегі нәтижелі айнымалы мен ескерілетін факторлар (түсіндіруші айнымалылар) арасындағы байланыс тығыздылығын көрсетеді.

Көптік детерминация және корреляция коэффиценттерінің арасындағы байланысты ескере отырып, мынадай формула аламыз:

немесе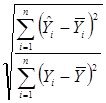

Бір факторлы үлгіде -1 < R<1.

Көп факторлы үлгіде 0 < R < 1.

R мәнінің ноль санына жақынырақ болуы сызықтық байланыстың жоқтығымен сипатталады, бірақ бұл жағдайда тығыз сызықсыз байланыстың болуы әбден мүмкін.

R мәнінің бір санына жақынырақ болуы – сызықты өсіп отыратын тәуелділіктің болуымен, R мәнінің минус бір санына жақынырақ болуы – сызықты азайып отыратын тәуелділіктің болуымен сипатталады.

Жеке корреляция.

Интенсивті (қарқынды) байланыстар жеке корреляция көмегімен келесідей жағдайларда бағаланады:

- талдауға қосылған бір айнымалының басқа қалған жиынтық айнымалылармен байланыс тығыздылығын анықтағанда;

- қалған айнымалыларды қоспағандағы екі айнымалы арасындағы байланыс тығыздылығын анықтағанда.

Жеке корреляция коэффиценттерін есептеу келесі формула арқылы жүзеге асырылады:

Бұл формула практикалық есептеугы ыңғайлы немесе қолайлы болуы үшін келесідей түрге келтірілуі мүмкін:

немесе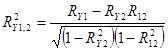

6 Лекция. Сызықсыз регрессия.

Көптеген жағдайда шынайы өмірде экономикалық үрдістер сызықсыз регрессиялық тәуелділіктермен сипатталады.

Сызықсыз эконометрикалық үлгілерді құрғанда сызықсыз функционалдық тәуелділіктер қолданылады (дәрежелі, көрсеткішті, логарифмдік, тригонометриялық, әр түрлі дәрежелердің көпмүшелері және т.б.).

Сызықсыз регрессияның екі класы ажыратылады:

1. Айнымалыларға ( факторларға) ХК қатысты сызықсыз, бірақ эконометрикалық үлгінің белгісіз коэффиценттері бойынша сызықты.

Сызықсыз регрессияның бұл класы квазисызықтық регрессиялық тәуелділіктер деп аталады. Әрі қарай сызықсыз тәуелділіктердің бұл класының ерекшеліктері мен артықшылықтары көрсетіледі.

2. Айнымалыларға ( факторларға) ХК қатысты сызықсыз және эконометрикалық үлгінің белгісіз коэффиценттері бойынша да сызықсыз. Әрі қарай сызықсыз тәуелділіктердің бұл каласының ерекшеліктері мен жетіспеушіліктері көрсетіледі.

Полиномиальді квазисызықтық регрессиялық тәуелділікті қарастырайық .

Ŷ = b0+ b₁X+ b₂X²

Y → ҚР жалпы ішкі өнімі, Х → өнеркәсіптің дамуына инвестиция.

b₀, b₁, b₂ үлгі параметрлерін анықтау үшін келесідей қалыптасқан теңдеулер жүйесі құрылады:

Σ Y_і = nb₀+b₁ ΣX_і+b₂ ΣX_і²

Σ Y_і*X_і=b₀ ΣX_і+b₁ ΣX_і²+b₂ ΣX_і³

Σ Y_і*X_і²= b₀ ΣX_і²+b₁ ΣX_і³+b₂ ΣX_і⁴

Көрсетілген жүйені нақтылау үшін жұмыс кестесі құрылады

b₀, b₁, b₂ үш белгісізі бар үш теңдеулер жүйесін шешкенде үлгінің бұл параметрлерін анықтаймыз. ҚР жалпы ішкі өнімінің өнеркәсіптің дамуына инвестициядан тәуелділігінің сызықсыз эконометрикалық үлгісін аламыз.

Әрі қарай алынған үлгіні детерминация және корреляция коэффиценттері көмегімен бағалау жүзеге асырылады.