Алдын – ала анықталған айнымалылар

3. Алдын – ала анықталған айнымалылар.

а) жай экзогенді айнымалылар

б) кешеуілді экзогенді айнымалылар

в) кешеуілді эндогенді айнымалылар.

Біздің үлгіде алдын – ала анықталған айнымалылар экзогенділермен сәйкес келеді. Эндогенді және экзогенді кешеуілдеулі айнымалылар қатыспайды.

4. Өзара тәуелді айнымалылар. Өзара тәуелді айнымалы деп жай эндогенді айнымалыларды айтады. Олардың арасында көпжақты байланыс болғандықтан және эконометрикалық үлгінің біруақтылы теңдеулерімен анықталандықтан өзара тәуелді деп атаймыз.

Біздің үлгіде эндогенді айнымалылар (ақша айналысы мен ақша айналымы) өзара тәуелді айнымалыларды қатарында.

5. Ашулы немесе жасырын айнымалылар. Бұл айнымалылар теңдеуге кірмейді, бірақ өзара тәуелді айнымалыларға әсер етеді. Олардың табиғаты бір теңдеулі регрессияныкіне ұқсас.

13 Лекция. Біруақтылы эконометрикалық үлгілердің түрі.

1. Эконометрикалық үлгінің құрылымдық формасы.

АУ_t = BX_t + U_t t € 1,2,...,Т түріндегі үлгі құрылымдық деп аталады.

Ол бір және көп жақты стохастикалық себепті қатынастарды сипаттайды.

2. Толық эконометрикалық үлгі. Эконометрикалық үлгі толық болып есептеледі, егер:

1. ашулы айнымалы кездейсоқ сипатқа ие болып, өзара тәуелді айнымалыларға елеулі әсер ететін айнымалыларды қамтығанда .

2. оның құрамында қанша өзара тәуелді айнымалы болса, сонша теңдеу болғанда.

3. теңдеулер жүйесі өзара тәуелді айнымалыларға қатысты бір мәнді шешімге ие болғанда. Det A ≠ 0.

3. Эконометрикалық үлгінің келтірілген формасы.

Егер эконометрикалық үлгі толық болса, онда бар . онда

Эконометрикалық үлгінің алынған формасы келтірілген деп аталады.

белгілеп, аламыз.

Келтірілген форманың теңдеулер коэффиценті өзара тәуелді айнымалыларға алдын – ала анықталған айнымалылардың тікелей немесе жанама әсерін бейнелейді.

Құрылымдық форма коэффиценттері тікелей әсерді бейнелейді. Келтірілген формада әрбір теңдеу көптік регрессияның қатарында. Үлгі жаспарлау үшін пайдаланылады.

Келтірілген формадан құрылымдыға өтуге болмайды. Құрылымдық және келтірілген формалар айрықшылықты функцияларды орындайды, белгілі тапсырмаларды шешуге мүмкіндік береді.

4. Рекурсивті үлгі. Рекурсивті үлгі

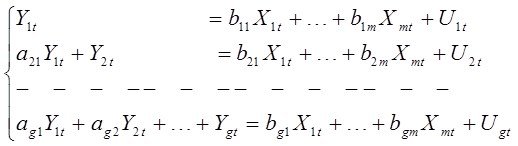түрінде болады.

Ерекшелік:

Бірінші деңгейде тек Ү_і бар, екінші деңгейде Ү_і – ге басқа эндогенді айнымалы қосылады. Үшінші деңгейде – Ү₃ т.с.с.

Айнымалылардың бұлай орналасуына тек эндогенді айнымалылар арасындағы бір жақты бағытталған тәуелділіктер қол жеткізеді.

Эндогенді айнымалылар бір себепті байланыс құрады.

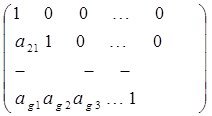бірлік диагоналі бойынша үшбұрышты матрица

5. Тәуелсіз теңдеулер жүйесі. (бір матрица) болғандағы рекурсивті үлгінің жеке жағдайы.

құрылымдық

келтірілген

14 Лекция.Серпінді эконометрикалық үлгілер.

Эконометрикалық үлгі серпінді болып уақыттың t берілген сәтінде ағымды және алдыңғы уақытқа жататын айнымалылар мәнін ескергенде табылады, яғни бұл үлгі уақыттың әрбір сәтіндегі зерттелетін айнымалылар динамикасын бейнелейді.

Бұндай үлгіге авторегрессия үлілері мен үлестірілген кешеуілді үлгілерді жатқызамыз.

Үлестірілген кешеуілді үлгілер келесідей түрде болады:

Ү_t = a +b₀X_t + b₁X_t-1 + b₂X_t-2 + ε_t

Авторегрессия үлгілері түрінде болады.

Кешеуілі үлестірілген үлгі жалпы келесідей түрде болады:

Берілген үлгі егер уақыттың t кейбір сәтінде Х факторында өзгеріс болса, онда ол өзгеріс Ү нәтижелі айнымалысының мәніне Р келесі уақыт сәттерінің ағымында ықпалын тигізетіндігін көрсетеді.

b0 регрессия коэфиценттері кейбір тіркелген уақыт t сәтінде Х факторының кешеуілді мәндерінің әсерін есептемегенде Х t өз өлшеуінің бір бірлікке өзгергендегі Ү t –нің орташа абсолютті өзгеруін сипаттайды. Бұл коэффицентті қысқа мерзімді мультипликатор деп атайды.

Ұқсастығына қарай (b₀ + b₁); (b₀ + b₁ + b₂); т.с.с. аралық мультипликатор деп атайды. Онда b₀ + b₁ + b₂ + ...+ b_l = В ұзақ мерзімді мультипликатор.

Β_j = b_j / b. Егер bj-дің барлық коэффиценттері бірдей белгілерге ие болса, онда кез келген j 0 < b_j < 1 немесе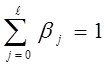

Бұл жағдайда β_j қатысты коэффиценттер b_j тиісті коэффиценттеріне таразы болып табылады.

Кешеуілі үлестірілген үлгілер құру. Кешеуілі үлестірілген жалпы үлгіні қарастырайық. Кешеуілдің полиномиальді құрылымы бар делік, яғни

1-ші дәрежелі полином;

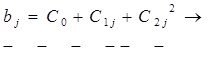1-ші дәрежелі полином; т.с.с

-дәрежелі полином

Онда b_j – ді үлгіде келесі түрде көрсетуге болады:

и т.д.

Жалпы үлгіге қойып, жіктеулерді қайта топтастырып және мәндерді енгізсек

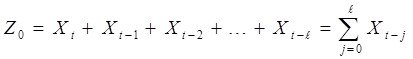
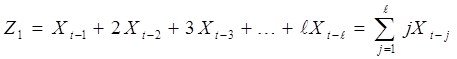
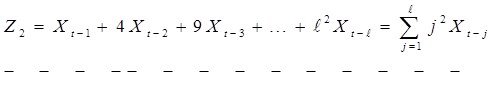
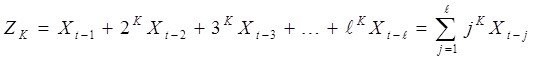
келесіні аламыз:

Әрі қарай ең кіші квадраттар әдісі қолданылады.

Үлгіні құрастыру алгаритмі.

1. l максималды шамасы анықталады.

2. К полиномының деңгейі анықталады.

3. Ζ айнымалысының мәні есептеледі.

4. үлгінің а,С0, С1,..., Ск параметрлері есептеледі.

5. кешеуілі үлестірілген бастапқы үлгі параметрлері есептеледі.

15 Лекция. Авторегрессия үлгілері.

Авторегрессия үлгісі Ү_t = a + b₀Х_t + C₁ Ү_t-1 + ε_t түрінде болады. Кешеуілі үлестірілген үлгідегідей b0 бұл үлгіде Хt-нің бір бірлікке өзгеру әсерімен Ү_t-нің қысқа мерзімді өзгеруін сипаттайды. Бірақ аралық және ұзақ мерзімді мультипликаторлар авторегрессия үлгілерінде өзгеше. Мұнда нәтиженің t+1 уақыт мезетінде жалпы абсолютті өзгеруі b₀*C₁ бірлікті құрайды. Осыған ұқсас t+2 уақыт мезетінде нәтиженің абсолютті өзгеруі b₀*C₂ бірлікті құрайды т.с.с. Осылайша, авторегрессия үлгісінде ұзақ мерзімді мультипликаторді қысқа мерзімді және аралық мультипликаторлардың сомасы (қосындысы) ретінде есептеуге болады.

Себебі , онда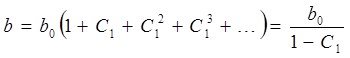

Авторегрессия үлгісін құру. Қарастырылған үлгілер l кешеуіл шамасы соңғы деп есептеліп құрылған. Егер кешеуіл шамасы шексіз десек.

Y_t = a+b₀X_t + b₁X_t-1 + b₂X_t-2 +…+ε_t

Фактордың нәтижеге кешеуіл әсері уақытында λ (0 < λ<1) тұрақты азаю темпі бар делік. Онда жалпы түріне b_j = b0*λ^j; j= 0,1,2,…, қойып

Y_t = a+b₀X_t + b₀ λX_t-1 + b₀λ²X_t-2 +…+ε_t аламыз.

t-1 үшін Y_t-1 = a+b₀X_t-1 + b₀ λX_t-2 + b₀λ²X_t-3 +…+ε_t жазуға болады.

Екі бөлігін де λ көбейтіп,бірінші выражениеден алып тастаймыз.

Y_t –λY_t-1= a – λ*a + b₀X_t + ε_t-1- λ ε_t-1

Немесе Y_t = a (1-λ) + b₀X_t +λY_t-1+U_t, мұнда U_t = ε_t - λ ε_t-1

Алынған үлгі екі факторлы сызықтың регрессияның, нақтырақ айтсақ авторегрессия үлгісі болып табылады.

Оның параметрлерін анықтап, λ және бастапқы үлгінің а мен b₀ параметрлерінң бағасын табамыз. Әрі қарай b_j= b₀* λ^j көмегімен бастапқы үлгінің b₁,b₂,…, параметрлерін еш қиындықсыз анықтаймыз.