Навигация
Некоторые главы мат. анализа
ГЛАВА 1 РЯДЫ И ИНТЕГРАЛ ФУРЬЕ
Основные сведения
Функция f(x), определенная на всей числовой оси называется периодической, если существует такое число ![]() , что при любом значении х выполняется равенство
, что при любом значении х выполняется равенство ![]() . Число Т называется периодом функции.
. Число Т называется периодом функции.
Отметим некоторые с в о й с т в а этой функции:
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т.
2) Если функция f(x) период Т , то функция f(ax) имеет период ![]() .
.
3) Если f(x) - периодическая функция периода Т , то равны любые два интеграла от этой функции, взятые по промежуткам длины Т (при этом интеграл существует), т. е. при любых a и b справедливо равенство 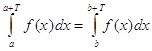 .
.
Тригонометрический ряд. Ряд Фурье
Если f(x) разлагается на отрезке ![]() в равномерно сходящийся тригонометрический ряд:
в равномерно сходящийся тригонометрический ряд:
![]() (1)
(1)
,то это разложение единственное и коэффициенты определяются по формулам:
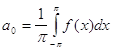
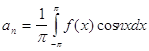
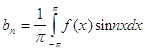 , где n=1,2, . . .
, где n=1,2, . . .
Тригонометрический ряд (1) рассмотренного вида с коэффициентами называется тригонометрическим рядом Фурье, а ![]() коэффициентами ряда Фурье.
коэффициентами ряда Фурье.
Достаточные признаки разложимости функции в ряд Фурье
Точка ![]() разрыва функции
разрыва функции ![]() называют точкой разрыва первого рода, если существует конечные пределы справа и слева этой функции в данной точке.
называют точкой разрыва первого рода, если существует конечные пределы справа и слева этой функции в данной точке.
ТЕОРЕМА 1 (Дирихле). Если ![]() периодическая с периодом
периодическая с периодом ![]() функция непрерывна или имеет конечное число точек разрыва 1-ого рода на отрезке [
функция непрерывна или имеет конечное число точек разрыва 1-ого рода на отрезке [![]() ] и этот отрезок можно разбить на конечное число частей, в каждом из которых f(x) монотонна, то ряд Фурье относительно функции сходится к f(x) в точках непрерывности и к среднеарифметическому односторонних пределов в точках разрыва рода (Функция удовлетворяющая этим условиям называется кусочно-монотонной).
] и этот отрезок можно разбить на конечное число частей, в каждом из которых f(x) монотонна, то ряд Фурье относительно функции сходится к f(x) в точках непрерывности и к среднеарифметическому односторонних пределов в точках разрыва рода (Функция удовлетворяющая этим условиям называется кусочно-монотонной).
ТЕОРЕМА 2. Если f(x) периодическая функция с периодом ![]() , которая на отрезке [
, которая на отрезке [![]() ] вместе со своей производной непрерывна или имеет конечное число точек разрыва первого рода, то ряд Фурье функции f(x) в точках разрыва к среднему арифметическому односторонних пределов (Функция удовлетворяющая этой теореме называется кусочно-гладкой).
] вместе со своей производной непрерывна или имеет конечное число точек разрыва первого рода, то ряд Фурье функции f(x) в точках разрыва к среднему арифметическому односторонних пределов (Функция удовлетворяющая этой теореме называется кусочно-гладкой).
Ряды Фурье для четных и нечетных функций
Пусть f(x) - четная функция с периодом 2L , удовлетворяющая условию f(-x) = f(x) .
Тогда для коэффициентов ее ряда Фурье находим формулы:
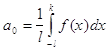 =
=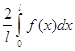
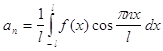 =
=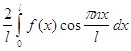
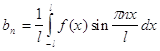 = 0
= 0![]() , где n=1,2, . . .
, где n=1,2, . . .
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2L выглядит так:
![]()
Пусть теперь f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
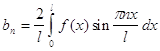 , где n=1,2, . . .
, где n=1,2, . . .
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
![]()
Если функция f(x) разлагается в тригонометрический ряд Фурье на промежутке![]() то
то ![]()
, где ![]()
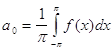 ,
,
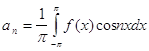 ,
,
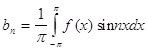 ,
,
Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо : доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.
Ряд Фурье по любой ортогональной системе функций
Последовательность функций ![]() непрерывных на отрезке [a,b], называется ортогональной системой функции на отрезке [a,b], если все функции последовательности попарно ортогональны на этом отрезке, т. е. если
непрерывных на отрезке [a,b], называется ортогональной системой функции на отрезке [a,b], если все функции последовательности попарно ортогональны на этом отрезке, т. е. если
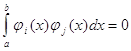
![]()
Система называется ортогональной и нормированной (ортонормированной) на отрезке [a,b],
если выполняется условие
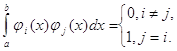
Пусть теперь f(x) - любая функция непрерывная на отрезке [a,b]. Рядом Фурье такой функции f(x) на отрезке [a,b] по ортогональной системе называется ряд:
![]()
коэффициенты которого определяются равенством:
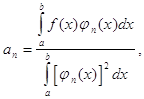 n=1,2,...
n=1,2,...
Если ортогональная система функций на отрезке [a,b] ортонормированная, то в этом случаи
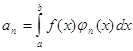 где n=1,2,...
где n=1,2,...
Пусть теперь f(x) - любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a,b]. Рядом Фурье такой функции f(x) на томже отрезке
по ортогональной системе называется ряд:
![]() ,
,
Если ряд Фурье функции f(x) по системе (1) сходится к функции f(x) в каждой ее точке непрерывности, принадлежащей отрезку [a,b]. В этом случае говорят что f(x) на отрезке [a,b] разлагается в ряд по ортогональной системе (1).
Комплексная форма ряда Фурье
Выражение ![]() называется комплексной формой ряда Фурье функции f(x), если
называется комплексной формой ряда Фурье функции f(x), если ![]() определяется равенством
определяется равенством
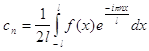 , где
, где ![]()
Переход от ряда Фурье в комплексной форме к ряду в действительной форме и обратно осуществляется с помощью формул:
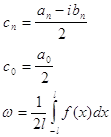
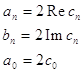 (n=1,2, . . .)
(n=1,2, . . .)
Задача о колебании струны
Пусть в состоянии равновесия натянута струна длинной l с концами x=0 и x=l. Предположим, что струна выведена из состояния равновесия и совершает свободные колебания. Будем рассматривать малые колебания струны, происходящие в вертикальной плоскости.
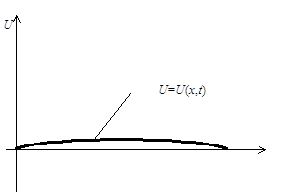
При сделанных выше допущениях можно показать, что функция u(x,t) , характеризующая положение струны в каждый момент времени t, удовлетворяет уравнению
![]() (1) , где а - положительное число.
(1) , где а - положительное число.
Наша з а д а ч а - найти функцию u(x,t) , график которой дает форму струны в любой момент времени t, т. е. найти решение уравнения (1) при граничных:
![]() (2)
(2)
и начальных условиях:
![]() (3)
(3)
Сначала будем искать решения уравнения (1), удовлетворяющие граничным условиям(2). Нетрудно увидеть, что u(x,t)![]() 0 является решением уравнения (1), удовлетворяющие граничным условиям(2). Будем искать решения, не равные тождественно 0, представимые в виде произведения u(x,t)=X(x)T(t),
(4) , где
0 является решением уравнения (1), удовлетворяющие граничным условиям(2). Будем искать решения, не равные тождественно 0, представимые в виде произведения u(x,t)=X(x)T(t),
(4) , где ![]() ,
, ![]() .
.
Подстановка выражения (4) в уравнение (1) дает:
![]()
Из которого наша задача сводится к отысканию решений уравнений:
![]()
Используя это условие X(0)=0, X(l)=0, докажем, что ![]() отрицательное число, разобрав все случаи.
отрицательное число, разобрав все случаи.
a) Пусть ![]() Тогда X”=0 и его общее решение запишется так:
Тогда X”=0 и его общее решение запишется так:
![]()
![]()
откуда ![]() и
и ![]() ,что невозможно , так как мы рассматриваем решения, не обращающиеся тождественно в нуль.
,что невозможно , так как мы рассматриваем решения, не обращающиеся тождественно в нуль.
б) Пусть ![]() . Тогда решив уравнение
. Тогда решив уравнение
![]()
![]()
получим ![]() , и, подчинив, найдем, что
, и, подчинив, найдем, что ![]()
в) ![]() Если
Если ![]() то
то
![]()
Уравнения имеют корни :
![]()
получим:
![]()
![]()
где ![]() -произвольные постоянные. Из начального условия найдем:
-произвольные постоянные. Из начального условия найдем:
![]()
откуда ![]() , т. е.
, т. е.
![]() (n=1,2,...)
(n=1,2,...)
![]() (n=1,2,...).
(n=1,2,...).
Учитывая это, можно записать:
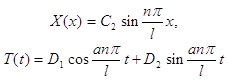 (n=1,2,...).
(n=1,2,...).
и, следовательно
![]() , (n=1,2,...),
, (n=1,2,...),
но так как A и B разные для различных значений n то имеем
![]() , (n=1,2,...),
, (n=1,2,...),
где ![]() и
и ![]() произвольные постоянные, которые попытаемся определить таким образом, чтобы ряд удовлетворял уравнению (1), граничным условиям (2) и начальным условиям (3).
произвольные постоянные, которые попытаемся определить таким образом, чтобы ряд удовлетворял уравнению (1), граничным условиям (2) и начальным условиям (3).
Итак, подчиним функцию u(x,t) начальным условиям, т. е. подберем ![]() и
и ![]() так , чтобы выполнялись условия
так , чтобы выполнялись условия
![]()
![]()
Эти равенства являются соответственно разложениями функций ![]() и
и ![]() на отрезки [0, l] в ряд Фурье по синусам. ( Это значит что коэффициенты будут вычисляться как для нечетной функций). Таким образом, решение о колебании струны с заданным граничными и начальными условиями дается формулой
на отрезки [0, l] в ряд Фурье по синусам. ( Это значит что коэффициенты будут вычисляться как для нечетной функций). Таким образом, решение о колебании струны с заданным граничными и начальными условиями дается формулой
![]()
где
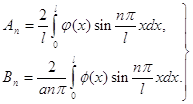 (n=1,2,...)
(n=1,2,...)
Интеграл Фурье
Достаточные условия представимости функции в интеграл Фурье.
Для того, чтобы f(x) была представлена интегралом Фурье во всех точках непрерывности и правильных точках разрыва, достаточно:
1) абсолютной интегрируемости на ![]()
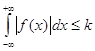 (т.е. интеграл сходится)
(т.е. интеграл сходится)
2) на любом конечном отрезке [-L, L] функция была бы кусочно-гладкой
3) в точках разрыва функции, ее интеграл Фурье определяется полусуммой левого и правого пределов в этих точках, а в точках непрерывности к самой функции f(x)
Интегралом Фурье функции f(x) называется интеграл вида:
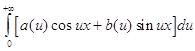
, где 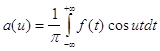 ,
,
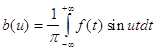 .
.
Интеграл Фурье для четной и нечетной функции
Пусть f(x)-четная функция, удовлетворяющая условиям представимости интегралом Фурье.
Учитывая, что 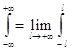 , а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (2) получаем:
, а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (2) получаем:
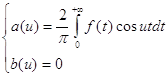 (3)
(3)
Таким образом, интеграл Фурье четной функции f(x) запишется так:
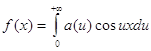 ,
,
где a(u) определяется равенством (3).
Рассуждая аналогично, получим, для нечетной функции f(x) :
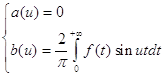 (4)
(4)
и, следовательно, интеграл Фурье нечетной функции имеет вид:
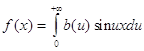 ,
,
где b(u) определяется равенством (4).
Комплексная форма интеграла Фурье
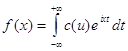 , (5)
, (5)
где
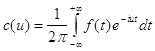 .
.
Выражение в форме (5) является комплексной формой интеграла Фурье для функции f(x).
Если в формуле (5) заменить c(u) его выражением, то получим:
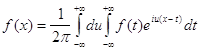 , где правая часть формулы называется двойным интегралом
, где правая часть формулы называется двойным интегралом
Фуpье в комплексной форме. Переход от интеграла Фурье в комплексной форме к интегралу
в действительной форме и обратно осуществим с помощью формул:
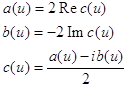
Формулы дискретного преобразования Фурье
Обратное преобразование Фурье.
![]()
![]()
где n=1,2,... , k=1,2,...
Дискретным преобразованием Фурье - называется N-мерный вектор ![]()
![]()
при этом, ![]() .
.
Разложение четной функции в ряд
Данную выше функцию сделаем четной(см. теорию), и рассмотрим ее на промежутке от 0 до ![]() смотри рис.2
смотри рис.2
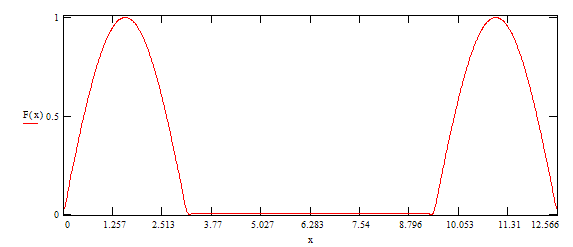
Рис.2
поэтому разложение по косинусу имеет вид:
![]()
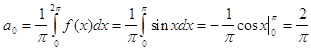
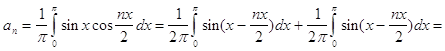
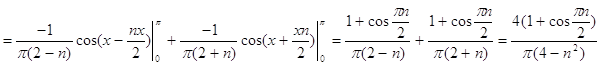
Из разложения видим что при n=2 дробь теряет смысл поэтому отдельно рассмотрим разложения первого и второго коэффициента суммы:
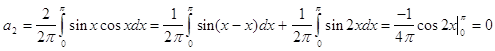
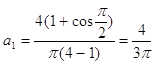
На основе данного разложения запишем функцию в виде ряда:
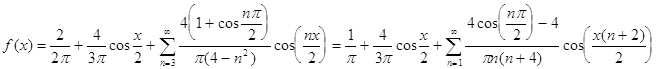
и вообще
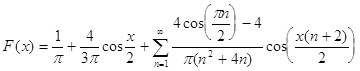 .
.
Найдем первые пять гармоник для найденного ряда:
1-ая гармоника ![]()

2-ая гармоника ![]()
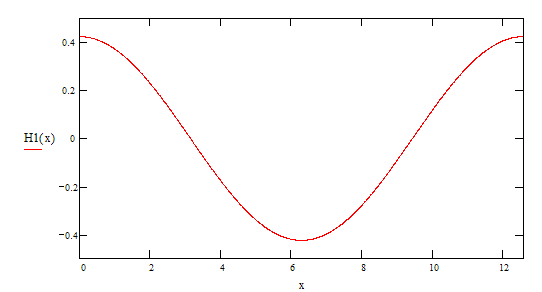
3-я гармоника ![]()
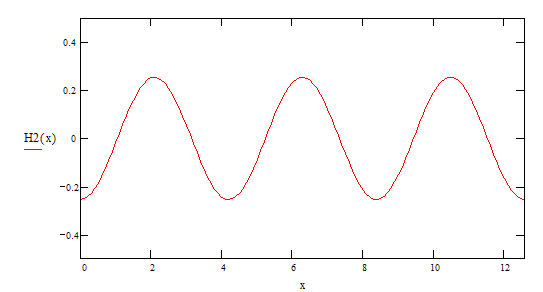
4-ая гармоника ![]()
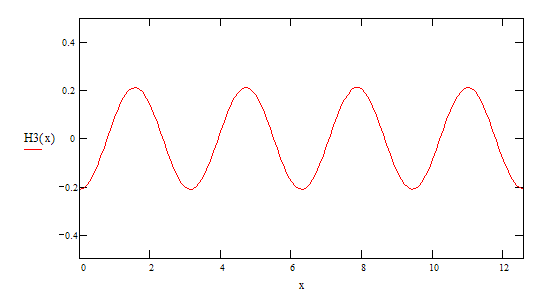
5-ая гармоника ![]()
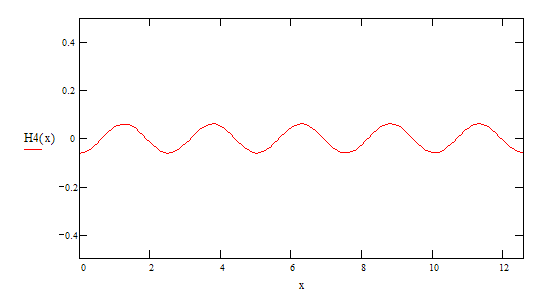
А теперь рассмотрим сумму этих гармоник F(x):
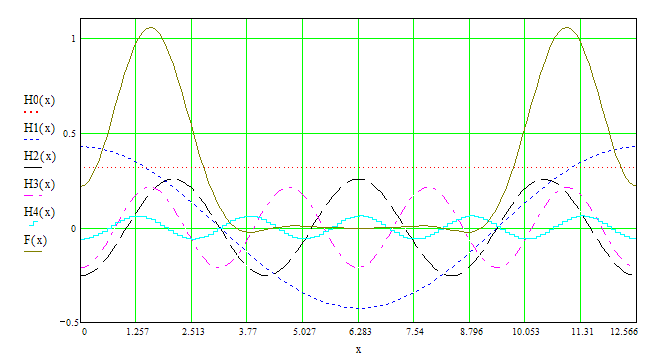
Комплексная форма ряда по косинусам
Для рассматриваемого ряда получаем коэффициенты (см. гл.1)
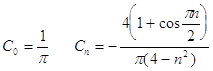 ,
,
но при ![]() не существует, поэтому рассмотрим случай когда n=+2 :
не существует, поэтому рассмотрим случай когда n=+2 :
![]() (т.к.
(т.к. ![]() см. разложение выше)
см. разложение выше)
и случай когда n=-2:
![]() ( т.к.
( т.к. 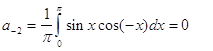 )
)
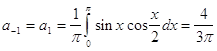
И вообще комплексная форма:
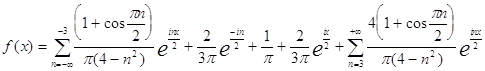
или
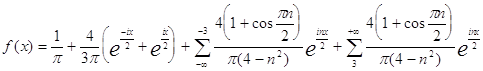
или
![]()
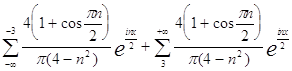
Разложение нечетной функции в ряд
Аналогичным образом поступаем с данной функцией F(x), продлевая ее как нечетную, и рассматриваем на промежутке от 0 до ![]() смотри рис.3
смотри рис.3
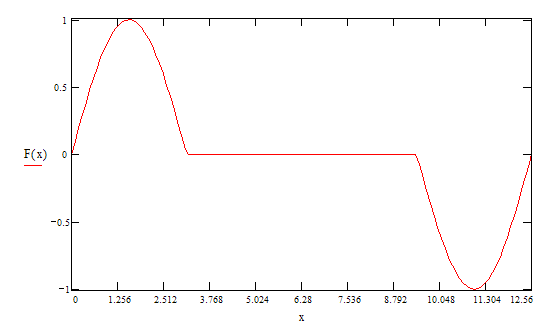
Рис.3
поэтому разложение по синусам имеет вид:
![]()
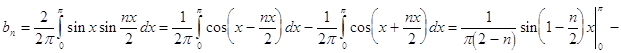
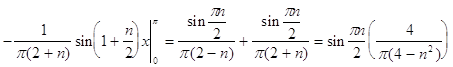
Из данного разложения видно, что при n=2 произведение неопределенно (можно не учесть часть суммы), поэтому рассмотрим два отдельных случая.
При n=1:
![]() ,
,
и при n=2:
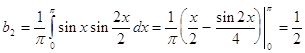
Учитывая данные коэффициенты имеем разложения в виде
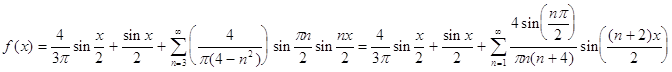
и вообще
![]()
Найдем первые пять гармоник для данного разложения:
1-ая гармоника ![]()
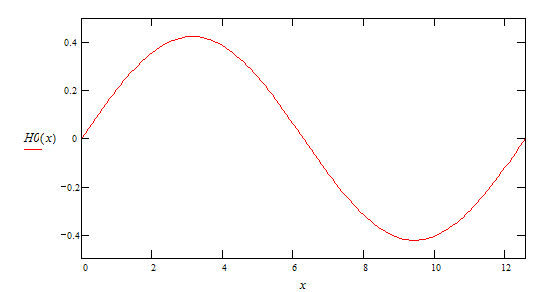
2-ая гармоника ![]()
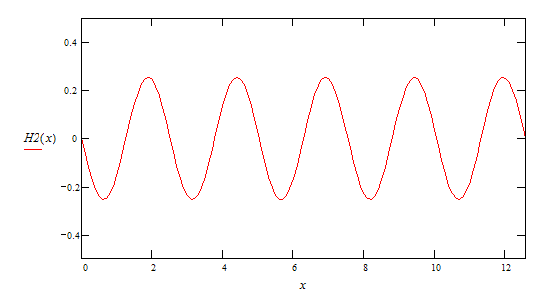
3-ая гармоника ![]()
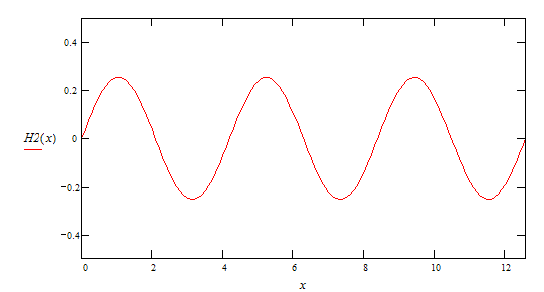
4-ая гармоника ![]()
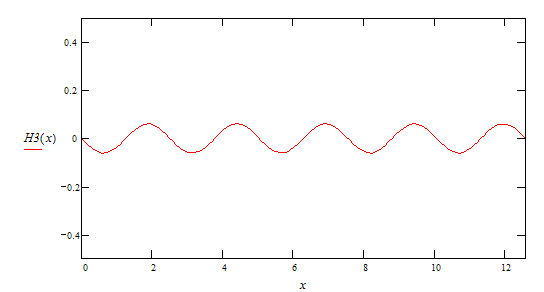
5-ая гармоника ![]()
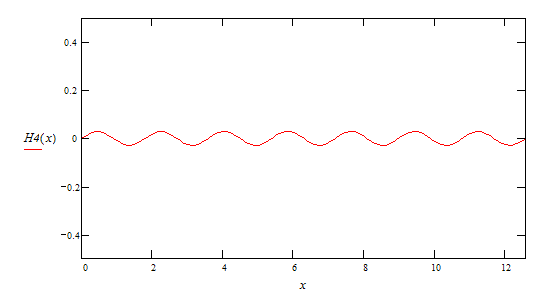
И просуммировав выше перечисленные гармоники получим график функции F(x)
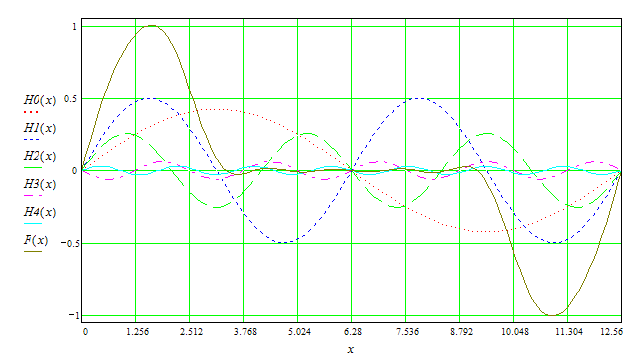 Вывод:
Вывод:
На основании главы 2, разложение функции в тригонометрический ряд(рис.1), разложение в ряд по косинусам(рис.2), разложение по синусам(рис.3), можно заключить, что данная функция разложима в тригонометрический ряд и это разложение единственное. И проанализировав суммы первых пяти гармоник по каждому разложению можно сказать, что наиболее быстрее к заданному графику достигается при разложении по синусам.
Комплексная форма ряда по синусам
Основываясь на теорию (см. гл.1) для ряда получаем:
![]() ,
, ![]() (т.к.
(т.к. ![]() )
)
тогда комплексный ряд имеет вид:
![]()
![]()
![]()
ГЛАВА 3 ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
Проверка условий представимости
Данную ранее функцию (см. гл. 2) доопределим на всей прямой от ![]() до
до ![]() как равную нулю(рис.4).
как равную нулю(рис.4).
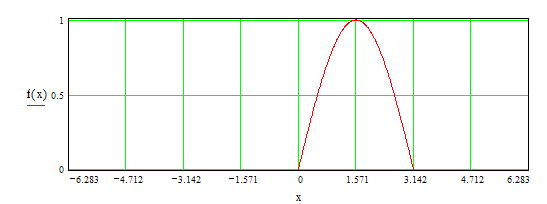
Рис.4
а) f(x)-определенна на R;
б) f(x)
возрастает на ![]() , f(x) убывает на
, f(x) убывает на ![]() - кусочнo-монотонна.
- кусочнo-монотонна.
f(x) = const на ![]() и
и ![]() .
.
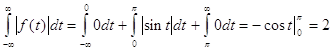 <
< ![]() .
.
Интеграл Фурье
В соответствии с теорией (см. гл. 1) найдем a(u) и b(u):
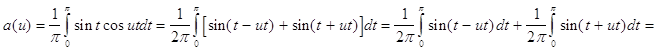
![]()
![]()
![]() ;
;
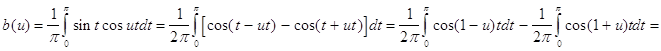
![]()
![]() .
.
И в конечном варианте интеграл Фурье будет выглядеть так:
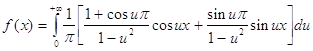
Интеграл Фурье в комплексной форме
Теперь представим интеграл Фурье в комплексной форме. На основе выше полученных разложений имеем:
![]() ,
,
![]() ,
,
а теперь получим интеграл в комплексной форме:
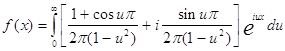 .
.
ГЛАВА 4 ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ПОЛИНОМОМ ЛЕЖАНДРА
Основные сведения
Функцию можно разложить в ортонормированной системе пространства X=[-1,1] , причем полиномы получим, если проинтегрируем выражение:
![]()
Соответственно получим для n=0,1,2,3,4,5, ... :
![]()
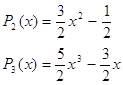
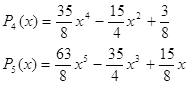
. . . . . . . . . .
Для представления функции полиномом Лежандра необходимо разложить ее в ряд:
![]() ,
,
где 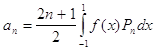 и разлагаемая функция должна быть представлена на отрезке от -1 до 1.
и разлагаемая функция должна быть представлена на отрезке от -1 до 1.
Преобразование функции
Наша первоначальная функция имеет вид (см. рис. 1):
![]()
т. к. она расположена на промежутке от 0 до ![]() необходимо произвести замену, которая поместит функцию на промежуток от -1 до 1.
необходимо произвести замену, которая поместит функцию на промежуток от -1 до 1.
Замена:
![]()
и тогда F(t) примет вид
![]()
или
![]()
Вычисление коэффициентов ряда
Исходя из выше изложенной формулы для коэффициентов находим:
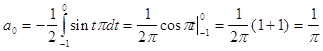
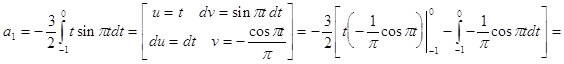
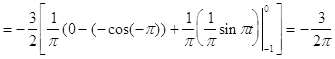
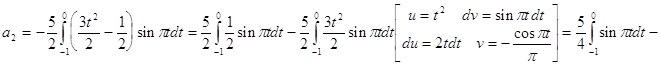
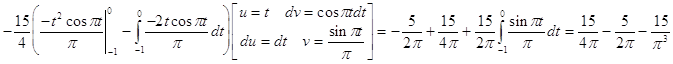
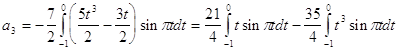
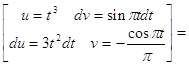
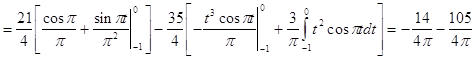
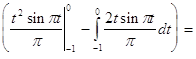
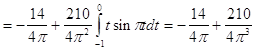
Далее вычисление коэффициентов осложнено, поэтому произведем вычисление на компьютере в системе MathCad и за одно проверим уже найденные:
![]()
![]()
![]()
![]()
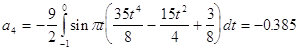
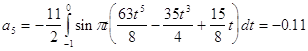
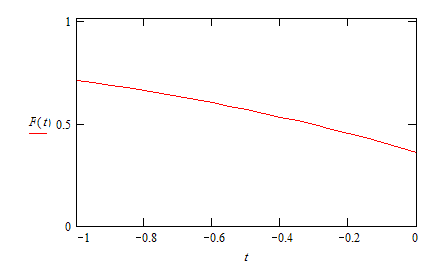
Рассмотрим процесс стремления суммы полинома прибавляя поочередно ![]() - слагаемое:
- слагаемое:
![]()

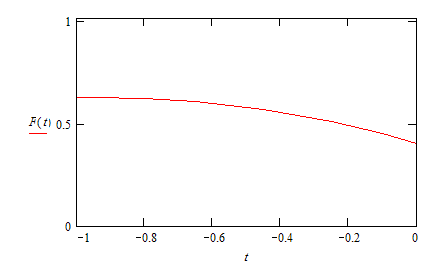
![]()
![]()
![]()
![]()
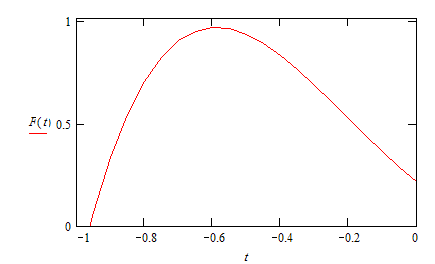
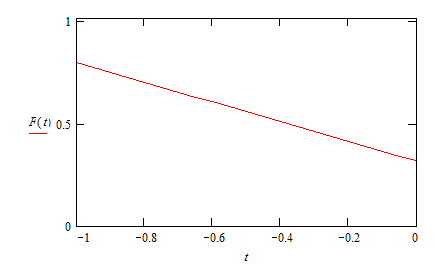
А теперь рассмотрим график суммы пяти полиномов F(t) на промежутки от -1 до 0 (рис.5):
![]()
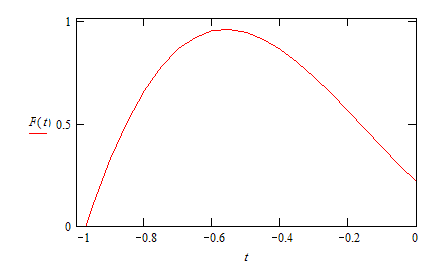
Рис. 5
т.к. очевидно, что на промежутке от 0 до 1 будет нуль.
Вывод:
На основе расчетов гл.2 и гл.4 можно заключить, что наиболее быстрое стремление из данных разложений к заданной функции достигается при разложении функции в ряд.
ГЛАВА 5 ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Прямое преобразование
Для того, чтобы произвести прямое преобразование, необходимо задать данную функцию (гл. 1, рис. 1) таблично. Поэтому разбиваем отрезок от 0 до ![]() на N=8 частей, так чтобы приращение:
на N=8 частей, так чтобы приращение:
![]()
В нашем случае ![]() , и значения функции в k-ых точках будет:
, и значения функции в k-ых точках будет:
![]()
для нашего случая ![]() (т.к. a=0).
(т.к. a=0).
Составим табличную функцию:
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 0 | 0.785 | 1.571 | 2.356 | 3.142 | 3.927 | 4.712 | 5.498 |
|
| 0 | 0.707 | 1 | 0.707 | 0 | 0 | 0 | 0 |
Табл. 1
Прямым дискретным преобразованием Фурье вектора ![]() называется
называется ![]() . Поэтому найдем :
. Поэтому найдем :
![]() , n=0,1,...,N-1
, n=0,1,...,N-1
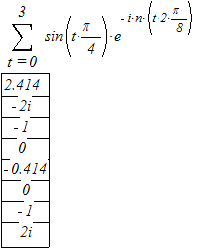
Сумму находим только до 3 слагаемого, т.к. очевидно, что от 4 до 7 к сумме суммируется 0 (т.к. значения функции из таблицы равны нулю).
Составим таблицу по прямому дискретному преобразованию:
зная, ![]() , где
, где ![]()
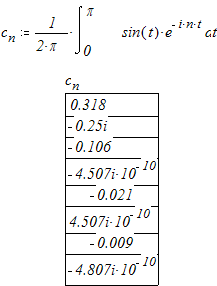
![]() , где
, где ![]()
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 2,4 | 2 | 1 | 0 | 0.4 | 0 | 1 | 2 |
|
| 0.318 | 0.25 | 0.106 | 0 | 0.021 | 0 | 0.009 | 0 |
Табл. 2
Амплитудный спектр ![]()
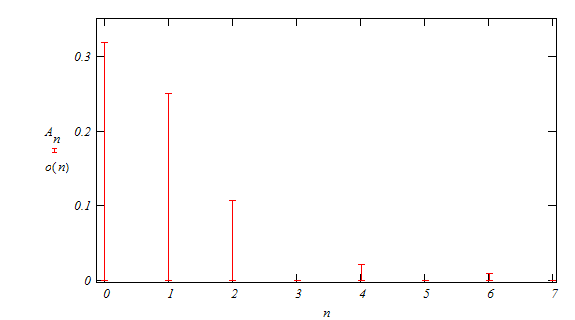
Обратное преобразование
Обратимся к теории гл.1. Обратное преобразование- есть функция :
![]()
В нашем случаи это:
![]()
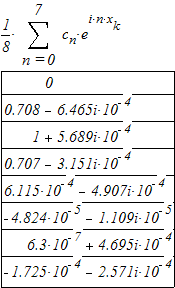
А теперь найдем модули ![]() и составим таблицу по обратным дискретным преобразованиям:
и составим таблицу по обратным дискретным преобразованиям:
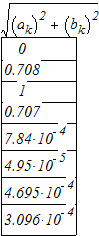
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
| 0 | 0.785 | 1.571 | 2.356 | 3.142 | 3.927 | 4.712 | 5.498 |
|
| 0 | 0.707 | 1 | 0.707 | 0 | 0 | 0 | 0 |
|
| 0 | 0.708 | 1 | 0.707 | 8e-4 | 5e-5 | 5e-4 | 3e-4 |
Табл. 3
Из приведенной таблицы видно, что ![]() приближенно равно
приближенно равно ![]() .
.
Построим графики используя табл.3, где ![]() - это F(k), а
- это F(k), а ![]() - это f(k) рис. 6 :
- это f(k) рис. 6 :
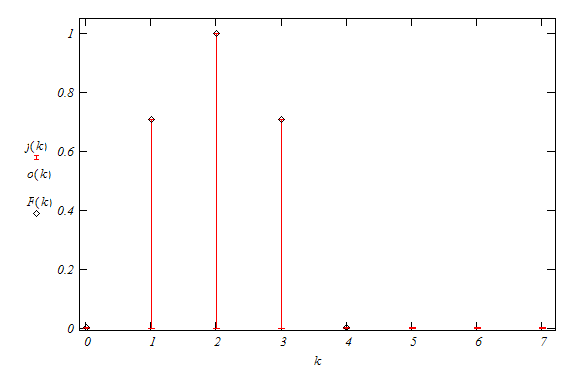
Рис. 6
Вывод:
На основе проделанных расчетов можно заключить, что заданная функция представима в виде тригонометрического ряда Фурье, а также интеграла Фурье, полинома Лежандра и дискретных преобразований Фурье. О последнем можно сказать, что спектр (рис. 6) прямого и обратного преобразований совпадают с рассматриваемой функцией и расчеты проведены правильно.
Этап I
Похожие работы
... управленческие решения, которые смогут обеспечить рациональное использование материальных ресурсов, снижение затрат, повышение рентабельности и создание условий для роста производства. [12, с. 27] ГЛАВА 2. Анализ использования материальных ресурсов ООО «ЖКХ «Сервис» 2.1 Краткая экономическая характеристика объекта исследования (ООО «ЖКХ «Сервис») Жилищно-коммунальное хозяйство имеет ...
... по данным публичной финансовой отчетности, составляют: - анализ абсолютных показателей прибыли; - анализ относительных показателей рентабельности; - анализ финансового состояния, рыночной устойчивости, ликвидности баланса, платежеспособности предприятия; - анализ эффективности использования заемного капитала; - экономическая диагностика финансового состояния предприятия и рейтинговая оценка ...
... работы организации и ее подразделений; изыскание финансовых возможностей улучшения обслуживания контингента предприятий. Источники информации для экономического анализа - это формы бухгалтерской отчетности, данные бухгалтерского учета, статистическая отчетность и другие источники, аналогичные применяемым в экономическом анализе предприятий. Под предметом экономического анализа понимаются ...
... и т.д. Поэтому первостепенной задачей в этом направлении является рациональное использование рабочего времени при эксплуатации ведущего оборудования. Далее при анализе организации основного производства необходимо рассчитать следующие показатели: Частные показатели технического уровня производства Коэффициент механизации и автоматизации производства Коэффициент использования технологических ...



0 комментариев