Антон выполняет просьбу Бориса
Используя однонаправленную функцию, Антон преобразует 7-значный идентификатор своего чудачества в другое 7-значное число
ПРИНЦИПЫ
АЛГОРИТМЫ
Внесетевые платежные системы
Карты памяти
Расчеты пластиковыми карточками в рамках INTERNET
Цифровые деньги и их характеристики
Стандарты электронных расчетов
Цифровые деньги и законодательство
Навигация
ПРИНЦИПЫ
Криптографические протоколы
129905
знаков
0
таблиц
3
изображения
1. ПРИНЦИПЫ.
Идея цифровой подписи, как законного средства подтверждения подлинности и авторства документа в электронной форме, впервые была сформулирована явно в 1976 году в статье двух молодых американских специалистов по вычислительным наукам из Стэндфордского университета Уитфилда Диффи и Мартина Хеллмана.
Суть ее состоит в том, что для гарантированного подтверждения подлинности информации, содержащейся в электронном документе, а также для возможности неопровержимо доказать третьей стороне (партнеру, арбитру, суду и т.п.), что электронный документ был составлен именно конкретным лицом, или по его поручению, и именно в том виде, в которм он предъявлен, автору документа предлагается выбрать свое индивидуальное число ( называемое обычно индивидуальным ключом, паролем, кодом, и т.д.) и каждый раз для "цифрового подписывания" сворачивать (замешивать) этот свой индивидуальный ключ, хранимый в секрете от всех, с содержимым конкретного электронного документа. Результат такого "сворачивания" - другое число, и может быть назван цифровой подписью данного автора под данным конкретным документом.
Для практического воплощения этой идеи требовалось найти конкретные и конструктивные ответы на следующие вопросы:
Как "замешивать" содержание документа с индивидуальным ключом пользователя, чтобы они стали неразделимы ?
Как проверять, что содержание подписываемого документа и индивидуальный ключ пользователя были подлинными, не зная заранее ни того, ни другого ?
Как обеспечить возможность многократного использования автором одного и того же индивидуального ключа для цифрового подписывания большого числа электронных документов ?
Как гарантировать невозможность восстановления индивидуального ключа пользователя по любому количеству подписанных с его помощью электронных документов ?
Как гарантировать, что положительным результат проверки подлинности цифровой подписи и содержимого электронного документа будет в том и только в том случае, когда подписывался именно данный документ и именно с помощью данного индивидуального ключа ?
Как обеспечить юридическую полноправность электронного документа с цифровыми подписями, существующего только в электронном виде без бумажного дубликата или заменителей ?
Для полноценных удовлетворительных ответов на все эти вопросы потребовалось около 20 лет. Сейчас мы можем точно и определенно сказать, что практические ответы на все эти вопросы получены. Мы располагаем полноценным арсеналом технических средств авторизации электронных документов, называемым цифровой подписью.
Рассмотрим эти ответы подробнее. Основная идея Диффи и Хеллмана состояла в том, чтобы искать ответы на первые четыре из списка вопросов (математические) по следующей схеме:
пользователи располагают средствами выбирать случайно свои индивидуальные ключи для подписывания из очень большого множества всех возможных ключей,
по каждому конкретно выбранному индивидуальному ключу для подписывания легко вычислить парный к нему ключ для проверки подписей,
процедура вычисления ключа проверки из ключа подписывания широко известна, практически реализуема и гарантирует невозможность восстановления ключа подписывания,
процедуры подписывания и проверки подписи широко известны, в каждой из них используется только один из пары ключей, и гарантируется невозможность получения неверного ответа, а также невозможность восстановления ключа подписывания по ключу проверки.
Самым сложным из этих условий является, конечно же, гарантирование невозможности восстановления ключа подписывания по ключу проверки и любому количеству подписанных электронных документов.
Лучший из предложенных на сегодня учеными способов его выполнения состоит в том, чтобы использовать такие процедуры подписывания и проверки, что практическое восстановление ключей подписи по ключам проверки требует решения известной сложной вычислительной задачи. Поскольку задача является общеизвестно сложной, то если ее не научились решать за обозримое время все математики мира во все предыдущие столетия, то есть некоторая надежда, что ее не сумеют решить быстро и в ближайшем будущем.
Практический результат последующих 20 лет научных поисков таких задач оказался до некоторой степени парадоксальным: при всем многообразии известных сложных вычислительных задач, практически применимой оказалась одна. Это так называемая задача дискретного логарифмирования.
В простейшем варианте ее можно сформулировать так. Если заданы три больших целых положительных числа
a, n, x,
то располагая даже несложными арифметическими устройствами типа карманного калькулятора, или просто карандашом и бумагой, можно довольно быстро вычислить число
a**x
как результат умножения числа
a
на себя
x
раз,
а затем и остаток от деления этого числа нацело на n, записываемый как
b = a**x mod n
задача же дискретного логарифмирования состоит в том, чтобы по заданным числам
a, b, n
связанным таким соотношением, найти то число
x
из которого по этой формуле было вычислено число b.
Оказывается, что задача дискретного логарифмирования при правильном выборе целых чисел настолько сложна, что позволяет надеяться на практическую невозможность восстановления числа x, - индивидуального ключа подписывания, по числу b, применяемому в качестве ключа проверки.
Чтобы говорить более определенно о практической невозможности решить ту или иную вычислительную задачу, следует предварительно договориться о том, какие вычислительные мощности и мозговые ресурсы доступны тому, кто предположительно будет эту задачу решать. Поскольку давать конкретные оценки возможностей потенциальных мозговых ресурсов будущего "взломщика" системы цифровой подписи дело весьма сложное и неблагодарное, мы будем просто исходить из предположения, что он располагает полной информацией о наилучших известных мировой науке методах решения данной задачи.
Далее, если он располагает вычислительной системой общей мощностью, скажем, 1 миллиард (10**9 = 1 000 000 000) операций в секунду, а это мощность современного суперкомпьютера типа CRAY-3, то
- за сутки непрерывной работы такой системы может быть решена задача сложностью около 100 000 миллиардов (или 10**14) операций
- за месяц - около 3*(10**15),
- за год - около 3*(10**16),
- за 10 лет - около 3*(10**17),
- за 30 лет - около 10**18 операций.
Таким образом, даже если допустить, что потенциальный взломщик цифровой подписи располагает вычислительной системой эквивалентной по мощности 1000 суперкомпьютерам типа CRAY-3, то на выполнение вычислений объемом 10**21 операций ему потребовалось бы не менее 30 лет непрерывной работы всей системы, что с практической точки зрения означает невозможность их выполнения.
Поэтому, цифровая подпись с надежностью не менее 10**21 может считаться практически неподделываемой.
В этом месте автору обычно задают вопрос: "А что, если где-то в недрах специальных служб известны более совершенные методы решения этой задачи, которые могут быть применены для фальсификации цифровых подписей?"
В настоящее время ответ на него оказывается довольно простым. Если вы боитесь, что обычно предлагаемого при длине ключей в 64 байта запаса надежности в 10**18 - 10**21 недостаточно, применяйте алгоритмы с более длинными ключами. Современные цифровые процессоры Intel486 и Pentium позволяют за доли секунды вычислять и проверять цифровые подписи с ключами до 512 байт, а стойкость большинства широко применяемых методов цифровой подписи при такой длине ключей заведомо превосходит все разумные требования ( более чем 10**50).
Итак, как видим, современные принципы построения системы цифровой подписи, общепризнанные в мире, просты и изящны:
методы вычисления и проверки цифровых подписей всех пользователей системы одинаковы, всем известны и основываются на широко известных математических задачах,
методы вычисления ключей проверки цифровых подписей из индивидуальных ключей подписывания одинаковы для всех и хорошо известны, их надежность также основывается на широко известных математических задачах,
индивидуальные ключи подписывания выбираются самими пользователями по случайному закону из большого множества всех возможных ключей,
при конкретном алгоритме цифровой подписи его стойкость может быть оценена без привлечения какой-либо "закрытой" информации на основе только известных математических результатов и разумных допущений о вычислительных мощностях потенциального "взломщика", посколку она базируется на общедоступных теоретических результатах по оценке сложности широко известных сложных вычислительных задач.
Похожие работы
... На этапе коммуникации реализуется собственно протокол аутентифицированного ключевого обмена, который завершается формированием общего сеансового ключа. Дефекты в криптографических протоколах В последующих разделах рассматриваются протоколы с типичными дефектами. Примеры протоколов разбиты на группы по типу используемой криптосистемы: - протоколы с криптосистемой DH (Диффи, Хэллман); - ...
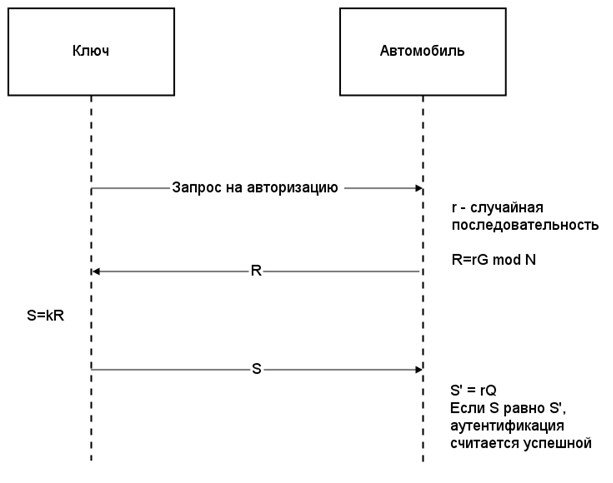
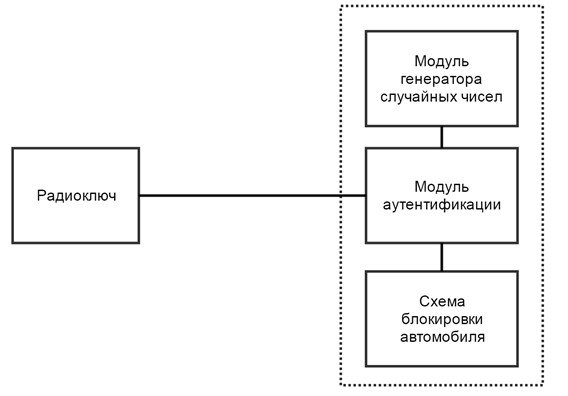
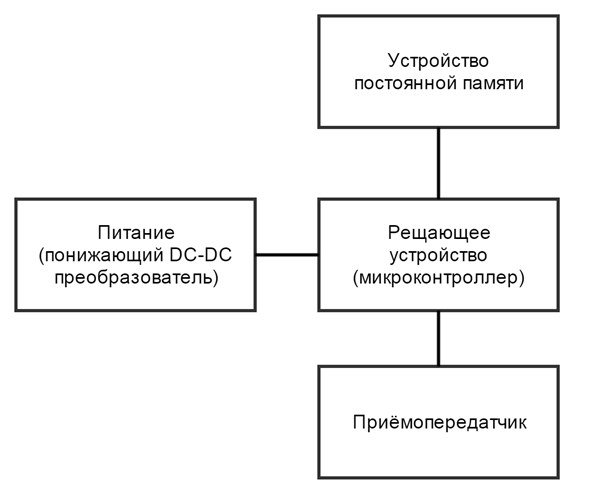
... является допустимым для устройства подобного рода. 5.3 Вывод В результате анализа параметров энергосбережения было выявлено то, что при реализации системы аутентификации пользователя транспортного средства нельзя обойтись без анализа энергопотребления системы и поиска путей уменьшения этого параметра. Изначально спроектированная система вызывала бы дискомфорт у пользователя за счёт излишне малого ...
... не к ключам!) и поэтому может зашифровывать и дешифровывать любую информацию; 2.7 Выводы по разделу 2. Подводя итоги вышесказанного, можно уверенно заявить, что криптографическими системами защиты называються совокупность различных методов и средств, благодаря которым исходная информация кодируеться, передаеться и расшифровываеться. Существуют различные криптографические системы защиты, ...
... в общем случае это может быть любое число, меньшее, чем длина алфавита. Это число и является ключом в данном шифре: А Б В Г Д Е Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Ь Ъ Э Ю Я Г Д Е Е Ж 3 И И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Ь Ъ Э Ю Я А Б В КРИПТОГРАФИЯ -> НУЛТХСЕУГЧЛВ Шифр Виженера Является модификацией шифра Цезаря, в котором величина сдвига является переменной и зависит от ключевого ...
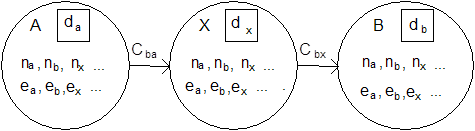
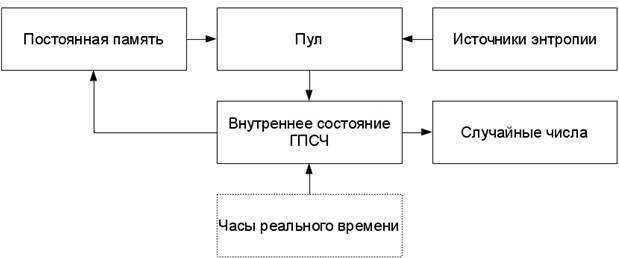
0 комментариев