АЛГОРИТМЫ

2. АЛГОРИТМЫ.

Проведем теперь сопоставление некоторых конкретных алгоритмов цифровой подписи с целью выявления их преимуществ и недостатков в различных ситуациях.

Для удобства оценки основных свойств того или иного алгоритма мы будем сравнивать его основные характеристики:

длину ключей,

длину цифровой подписи,

сложность (время) вычисления и

сложность (время) проверки подлинности цифровой подписи

при условии, что уровень стойкости подписи по отношению к любым методам фальсификации не ниже, чем 10**21 (или 30 лет непрерывной работы сети из 1000 суперкомпьютеров).

В качестве "базовой" длины ключей и длины самой цифровой подписи мы будем рассматривать длину в 64 байта.

RSA. Первым по времени изобретения конкретным алгоритмом цифровой подписи был разработанный в 1977 году в Массачусетском технологическом институте алгоритм RSA.

Алгоритм RSA основывается на том математическом факте, что задача дискретного логарифмирования при выборе целого параметра n в виде произведения двух различных простых чисел примерно равных по порядку величины, т.е.

n = p*q

становится не менее сложной, чем разложение n на эти простые множители, а последняя задача давно (еще со времен Архимеда и Евклида) известна в математике как сложная.

По современным оценкам сложность задачи разложения на простые множители при целых числах n из 64 байт составляет порядка 10**17 - 10**18 операций, т. е. находится где-то на грани досягаемости для серьезного "взломщика". Поэтому обычно в системах цифровой подписи на основе алгоритма RSA применяют более длинные целые числа n (обычно от 75 до 128 байт).

Это соответственно приводит к увеличению длины самой цифровой подписи относительно 64-байтного варианта примерно на 20% -100% (в данном случае ее длина совпадает с длиной записи числа n), а также от 70% до 800% увеличивает время вычислений при подписывании и проверке.

Кроме того, при генерации и вычислении ключей в системе RSA необходимо проверять большое количество довольно сложных дополнительных условий на простые числа p и q (что сделать достаточно трудно и чего обычно не делают, пренебрегая вероятностью неблагоприятного исхода - возможной подделки цифровых подписей)., а невыполнение любого из них может сделать возможным фальсификацию подписи со стороны того, кто обнаружит невыполнение хотя бы одного из этих условий (при подписывании важных документов допускать, даже теоретически, такую возможность нежелательно).

В дополнение ко всем этим алгоритмическим слабостям метода RSA следует также иметь в виду, что он защищен патентом США и поэтому любое его использование на территории США или западноевропейских стран требует приобретения соответствующей лицензии на использование, стоимость которой на 100 пользователей составляет $5000.

EGSA. Существенным шагом вперед в разработке современных алгоритмов цифровой подписи был новый алгоритм Т. ЭльГамаля, предложенный им в 1984 году. В этом алгоритме целое число n полагается равным специально выбранному большому простому числу p, по модулю которого и производятся все вычисления. Такой выбор позволяет повысить стойкость подписи при ключах из 64 байт примерно в 1000 раз, т.е. при такой длине ключей обеспечивается необходимый нам уровень стойкости порядка 10**21. Правда, при этом длина самой цифровой подписи увеличивается в два раза и составляет 128 байт.

Главная "заслуга" алгоритма ЭльГамаля состояла в том, что в дальнейшем он послужил основой для принятия нескольких стандартов цифровой подписи, в том числе национального стандарта США DSS, введенного в действие 1 декабря 1994 года и государственного стандарта РФ ГОСТ Р 34.10, введенного с 1 января 1995 года.

DSA. Национальным институтом стандартов и технологий СЩА в 1991 году на основе алгоритма ЭльГамаля был разработан и представлен на рассмотрение Конгресса США новый алгоритм цифровой подписи, получивший название DSA (сокращение от Digital Signature Algorithm). Алгоритм DSA, ставший в дальнейшем основой национального стандарта США на цифровую подпись имеет по сравнению с алгоритмом RSA целый ряд преимуществ:

во-первых, при заданном уровне стойкости цифровой подписи целые числа, с которыми приходится проводить вычисления, имеют запись как минимум на 20% короче, что соответственно уменьшает сложность вычислений не менее, чем на 70% и позволяет заметно сократить объем используемой памяти;

во-вторых, при выборе параметров достаточно проверить всего три достаточно легко проверяемых условия;

в-третьих, процедура подписывания по этому методу не позволяет вычислять (как это возможно в RSA) цифровые подписи под новыми сообщениями без знания секретного ключа.

Эти преимущества, а также соображения, связанные с возможностью его реализовывать любым разработчиком свободно без коммерческих лицензионных соглашений с держателями патента, компанией RSA Data Security, и возможностью свободного безлицензионного экспорта такой технологии из США послужили главным мотивом для принятия в 1994 году национального стандарта цифровой подписи (DSS) на его основе.

Такое решение отнюдь не было очевидным, поскольку RSA, как наиболее известный алгоритм цифровой подписи и шифрования с открытым ключом, был гораздо шире распространен, практически опробован во многих странах и признан как стандарт de facto большинством разработчиков операционных систем, сетевых технологий и прикладного программного обеспечения. Популярность его объясняется, прежде всего, 8-летним опережением по времени появления, значительно более широкой известностью как самого алгоритма, так и его авторов в научных кругах, а также успешным бизнесом держателя патента - компании RSA Data Security, Inc. (сам автор алгоритма ЭльГамаль был в 1994-1995 гг. ее сотрудником).

Технические преимущества алгоритма, о которых мы говорили выше видны были лишь специалистам в области криптографии. Однако, в данной ситуации именно они оказались определяющими, и мир получил далеко не худший по тем временам стандарт. В настоящее время алгоритм DSA уже не является лучшим из возможных алгоритмов цифровой подписи по техническим параметрам, но вероятность его принятия в качестве международного стандарта остается достаточно большой.

По сравнению с оригинальным алгоритмом ЭльГамаля метод DSA имеет одно важное преимущество, - при заданном в стандарте уровне стойкости, числа, участвующие в вычислении подписи, имеют длину по 20 байт каждое, сокращая общую длину подписи до 40 байт.

Поскольку большинство операций при вычислении подписи и ее проверке также производится по модулю из 20 байт, сокращается время вычисления подписи и объем используемой памяти.

В алгоритме ЭльГамаля длина подписи при таком уровне стойкости была бы равна 128 байт.

НОТАРИУС. Поскольку в 1991 году наиболее распространенной моделью персонального компьютера в СССР был AT/286(12) то мы в своих ранних алгоритмических разработках должны были максимально упростить лучшие из известных тогда алгоритмов цифровой подписи, чтобы их программная реализация на таком процессоре позволяла вычислять и проверять подпись под электронными документами за разумное время, скажем, 1-2 секунды при размере документа до 10 KB.

Такие упрощения не должны были, конечно, снижать стойкости алгоритма, но за счет модификации процедур вычисления и проверки цифровой подписи, должны были его ускорить достаточно, чтобы подписывание и проверка цифровой подписи под электронным документом не вызывала заметных задержек в процессе его обработки на персональном компьютере.

Первым результатом такой работы был созданный в конце 1992 года аналог алгоритма ЭльГамаля НОТАРИУС-1.Основное отличие алгоритма НОТАРИУС-1 от алгоритма ЭльГамаля состоит в том, что вместо обычной операции умножения целых чисел по модулю большого простого p, как это делается у ЭльГамаля, алгоритм НОТАРИУС-1 использует похожую операцию, эффект от использования которой состоит в том, что обеспечивая точно такой же уровень стойкости, что и умножение по модулю простого числа, эта операция гораздо эффективней вычисляется на распространенных процессорах Intel, Motorola и др.

Процедуры подписывания электронных документов и проверки цифровых подписей по алгоритму НОТАРИУС-1 выглядят аналогично соответствующим процедурам алгоритма ЭльГамаля, обеспечивают тот же уровень стойкости подписи, но выполняются быстрее.

Затем, аналогичным образом был усовершенствован алгоритм DSA, который послужил основой для алгоритма цифровой подписи, названного НОТАРИУС-D.

Реализация этого алгоритма на стандартном процессоре Intel486DX4(100) позволила добиться времени подписывания электронного документа объемом 1 KB вместе с его предварительным хэшированием в 0.014 сек., а времени проверки подписи под документами такого объема, - 0.027 сек.

Если же объем документа равен 100 KB , время подписывания составляет 0.124 сек., а время проверки - 0.138 сек. Длина подписи 40 байт, стойкость - 10**21.

Дальнейшее совершенствование алгоритмов подписывания и проверки произошло за счет использования совместно с нашими, также запатентованных в США и Германии идей немецкого криптографа Клауса Шнорра, который предоставил нам право использования своего алгоритма на территории стран СНГ. Совместное применение этих идей привело в 1996 году к разработке алгоритма НОТАРИУС-S, который при сохранении стойкости подписи позволил сократить ее длину еще на 32.5%. Для базового варианта с ключами из 64 байт длина подписи сократилась относительно DSA и НОТАРИСА-D с 40 байт до 27 байт. Соответственно уменьшилось время вычисления и проверки подписи. Стойкось осталась на том же уровне - 10**21.

Эти алгоритмические разработки позволили нам предложить пользователю широкий выбор программ с длинами цифровой подписи от 16 до 63 байт и уровнями стойкости, соответственно, от 10**14 (или несколько дней работы сети из несколькими десятков персональных компьютеров) до 10**54 (или более 100 миллиардов лет непрерывной работы любой мыслимой вычислительной системы обозримого будущего). Более детальные технические характеристики различных алгоритмов приведены ниже, в Таблице 1.

Автор надеется, что параметры алгоритмов, приведенные в таблице, дадут читателю возможность оценить их основные качества без дальнейших пространных комментариев. Дополнительных пояснений требуют только разделы таблицы, посвященные алгоритму ГОСТ 34.10.

ГОСТ34.10. Стандарт на электронную подпись ГОСТ34.10 был опубликован впервые Госстандартом РФ в мае 1994 года и введен в действие с 1 января 1995 года. В предварительном варианте он был введен в качестве ведомственного стандарта на цифровую подпись ЦБ РФ и использовался в этом качестве с сентября 1993 года по декабрь 1994 года. Алгоритмы вычисления и проверки подписи в ГОСТ34.10 устроены аналогично алгоритму DSA, но предварительная обработка электронных документов перед подписыванием (так называемое хэширование) выполняются по другому, существенно более медленному способу. К сожалению, разработчики допустили целый ряд досадных ошибок, которые есть даже в официальном тексте стандарта. Поэтому при реализации следует быть внимательным и не всегда следовать формальному тексту.

Мы рассматриваем следующие виды угроз:

1. Предполагаем, что попытки подделать подпись предпринимают не профессионалы. "Злоумышленники" могут располагать сетью из нескольких персональных компьютеров, общая вычислительная мощность которой равна 2*10⁸ операций/сек.

Предполагаем, что "противостоим" профессионалам с вычислительной системой общей мощностью до 10¹² операций/ сек. Это может быть сеть из нескольких десятков мощных современных суперкомпьютеров.

Предполагаем, что "противостоим" самой мощной государственной спецслужбе, располагающей возможностью ( и желанием ) создать для этой задачи сеть из сотен специализированных параллельных суперкомпьютеров с 1000 специальных мощных

( по 10¹³ оп./ сек.) процессоров каждый и практически неограниченной памятью.

Фантазии на тему будущего.

Фантазии на тему далекого будущего.

СЕРТИФИКАЦИЯ.

Принятые в различных странах в настоящее время процедуры сертификации, которые могут быть применены к программам или программно-аппаратным реализациям цифровой подписи, состоят в проверке соответствия, реализованных разработчиком алгоритмов описанным в официальных текстах стандартов.

В США, аккредитованные Национальным институтом стандартов и технологий лаборатории проводят тестирование процедуры порождения простых чисел, определяющих параметры алгоритма DSA, на основании опубликованных в тексте стандарта конкретных значений параметров и начальных установок процедуры генерации простых чисел, затем, при тестовых значениях параметров алгоритма, тестовых индивидуальных ключах и тестовых рандомизирующих значениях подписывания производится вычисление и проверка цифровых подписей под тестовыми примерами электронных документов. Таких циклов тестирования может быть довольно много - до нескольких десятков тысяч. Вся последовательность результатов предъявляется в лабораторию для сравнения с результатами работы эталонной программы на таких же значениях входных параметров. По результатам сравнения делается заключение о соответствии данной реализации цифровой подписи стандарту.

Таким же или примерно таким образом происходит процесс сертификации программ цифровой подписи и в ряде западноевропейских стран.

У нас ситуация оказывается, мягко говоря, парадоксальной. Поскольку в официальном тексте стандарта есть ошибки, которые, будь он реализован строго формально, привели бы к совершенно другому алгоритму цифровой подписи, о стойкости которого можно только догадываться (особенно при специальном "неудачном" выборе параметров), то проверить для программных или аппаратных реализаций "соответствие стандарту ГОСТ34.10" просто невозможно. Если реализация абсолютно точно соответствует формальному тексту стандарта с ошибками, то неясно, что это означает с точки зрения надежности подписи, а если при реализации эти ошибки были "учтены", то такая реализация не может соответствовать стандарту. Поэтому все бумаги, в которых в настоящее время такое соответствие декларируется, не означают абсолютно ничего.

Более разумный подход проявляется при сертификации в рамках Гостехкомиссии РФ программ цифровой подписи в классе программных средств защиты информации в от несанкционированного доступа и изменения. Согласно руководящих документов Гостехкомиссии программные или аппаратные средства, реализующие технологию цифровой подписи могут быть объективно оценены на предмат соответствия конкретным официально опубликованным требованиям по степени защиты информации от несанкционированного изменения путем ее подписывания цифровыми подписями.

ЛИЦЕНЗИРОВАНИЕ.

До последнего времени было не совсем ясно как будут наши законы трактовать вопросы распространения технологии цифровой подписи и, в частности возможность их экспорта. Дело в том, что при явном противоречии как с принципами построения систем цифровой подписи, так и просто со здравым смыслом чиновники некоторых ведомств пытались отнести эту технологию чуть ли не к разряду особо охраняемых государством наравне с ядерным или другими видами оружия массового поражения или сверх секретными специальными шифровальными средствами для особо важной государственной информации.

К счастью, за последнее время произошли заметные изменения, проясняющие ситуацию в этом вопросе. Президент РФ 26 августа 1996 года подписал Указ №1268, регламентирующий экспорт товаров и технологий двойного назначения. Согласно примечаниям к списку технологий двойного применения, на которые распространяется действие этого указа, из программного обеспечения, в том числе криптографического, экспорт которого из РФ регламентируется и требует специальных лицензий, сделаны следующие исключения.

Общедоступное:

а) проданное из фондов в розничные торговые точки и предназначенное для:

сделок по продаже в розницу;

сделок по высылке товаров по почте; или

сделок по телефонным заказам; и

б) разработанное для установки пользователем без дальнейшей реальной поддержки снабженцем

(продавцом), или

2. "В общественной сфере".

Кроме того, в тексте примечаний к указу, в части терминологии приводятся следующие интересные определения.

Криптография - дисциплина, включающая принципы, средства и методы преобразования информации в целях сокрытия ее содержания, предотвращения видоизменения или несанкционированного использования.

Криптография ограничена преобразованием информации с использованием одного или более секретных параметров (например, криптографических перемененных) или соответствующим управлением ключом.

Поскольку технология цифровой подписи:

очевидно, не обеспечивает сокрытия содержания подписанной информации,

не предотвращает ее видоизменения (содержимое подписанных документов можно видоизменять как угодно, и это собственно сама подпись никак не может предотвратить),

не обеспечивает и несанкционированного использования (подписанный электронный документ может быть точно также, как и бумажный использован не законно)

то получается, что она не относится к области криптографии вообще.

А что же, собственно, мы получаем благодаря этой технологии ?

Электронные деньги

Похожие работы

ТИПИЧНЫЕ ДЕФЕКТЫ В КРИПТОГРАФИЧЕСКИХ ПРОТОКОЛАХ

Скачать

24886

1

11

... На этапе коммуникации реализуется собственно протокол аутентифицированного ключевого обмена, который завершается формированием общего сеансового ключа. Дефекты в криптографических протоколах В последующих разделах рассматриваются протоколы с типичными дефектами. Примеры протоколов разбиты на группы по типу используемой криптосистемы: -     протоколы с криптосистемой DH (Диффи, Хэллман); -     ...

Анализ задачи построения системы аутентификации пользователя транспортного средства

Скачать

138113

3

22

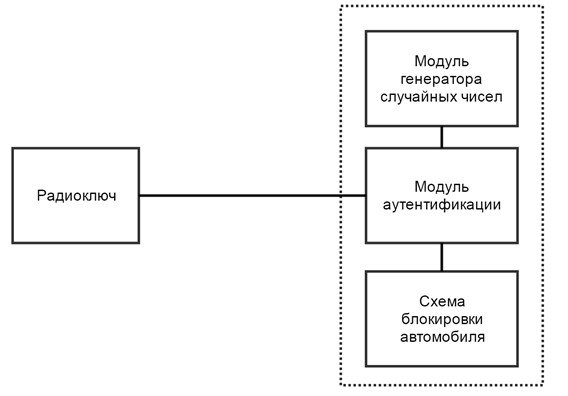
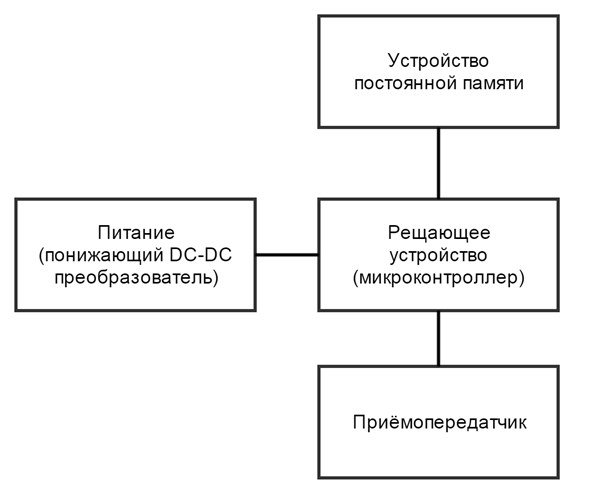
... является допустимым для устройства подобного рода. 5.3 Вывод В результате анализа параметров энергосбережения было выявлено то, что при реализации системы аутентификации пользователя транспортного средства нельзя обойтись без анализа энергопотребления системы и поиска путей уменьшения этого параметра. Изначально спроектированная система вызывала бы дискомфорт у пользователя за счёт излишне малого ...

Криптографические системы защиты данных

Скачать

61238

6

2

... не к ключам!) и поэтому может зашифровывать и дешифровывать любую информацию; 2.7 Выводы по разделу 2. Подводя итоги вышесказанного, можно уверенно заявить, что криптографическими системами защиты называються совокупность различных методов и средств, благодаря которым исходная информация кодируеться, передаеться и расшифровываеться. Существуют различные криптографические системы защиты, ...

Шпаргалки по криптографии

Скачать

78918

0

0

... в общем случае это может быть любое число, меньшее, чем длина алфавита. Это число и является ключом в данном шифре: А Б В Г Д Е Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Ь Ъ Э Ю Я Г Д Е Е Ж 3 И И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ы Ь Ъ Э Ю Я А Б В КРИПТОГРАФИЯ -> НУЛТХСЕУГЧЛВ Шифр Виженера Является модификацией шифра Цезаря, в котором величина сдвига является переменной и зависит от ключевого ...