Значения производных переменных ККИФ

2.4. Значения производных переменных ККИФ

Теперь дадим численно эффективный и точный метод для вычисления значений, 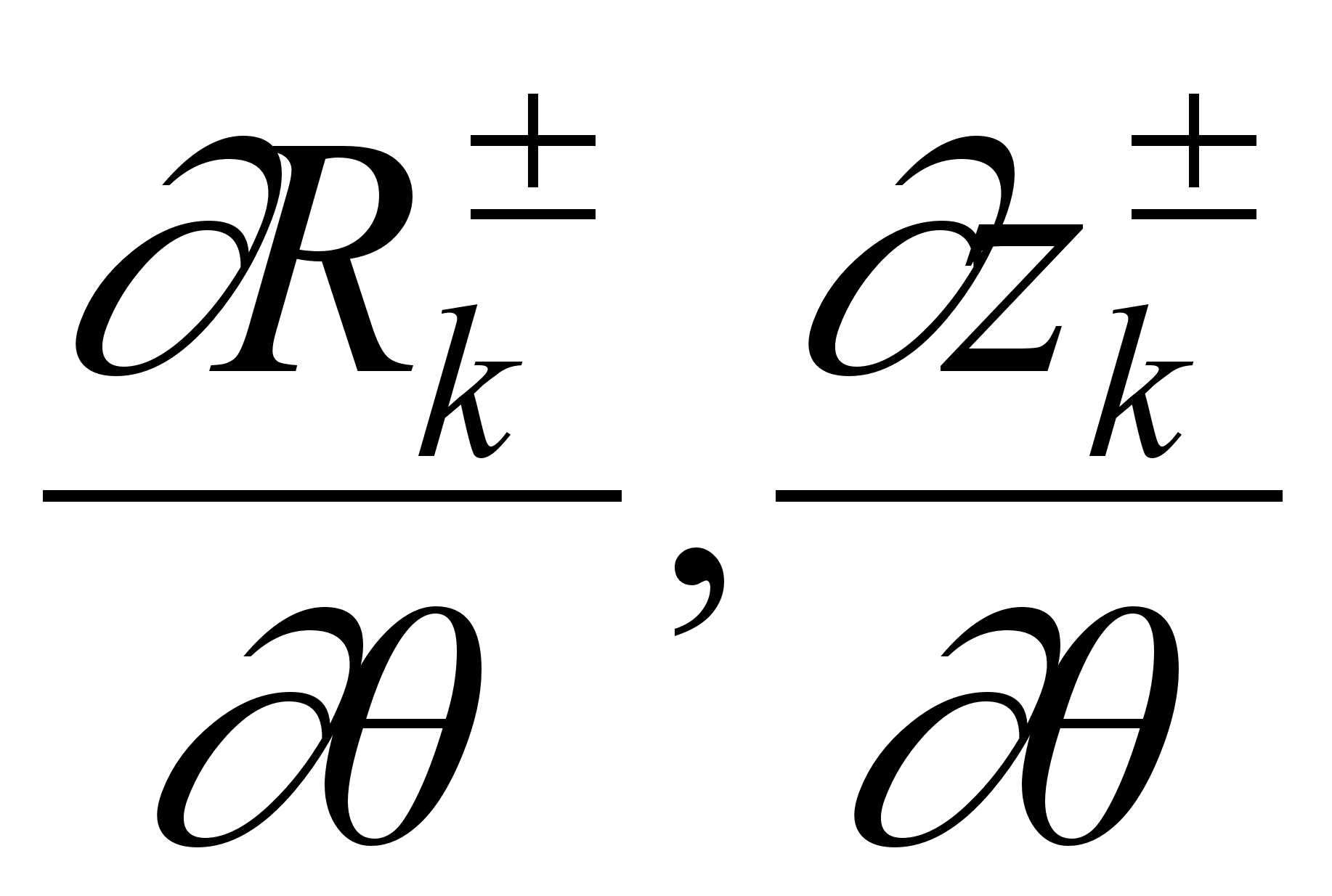, которые необходимы в формулах раздела 2.3.

Для упрощения понимания положим, что преобразования ККИФ (2.1.10) и (2.1.13) имеют вид:

(2.4.1)

где - прямоугольная матрица, - ортогональная, которая при умножении с дает верхнюю трапециевидную матрицу . Элементы матрицы дифференцируемые функции параметра . Тогда, при заданных значениях производных 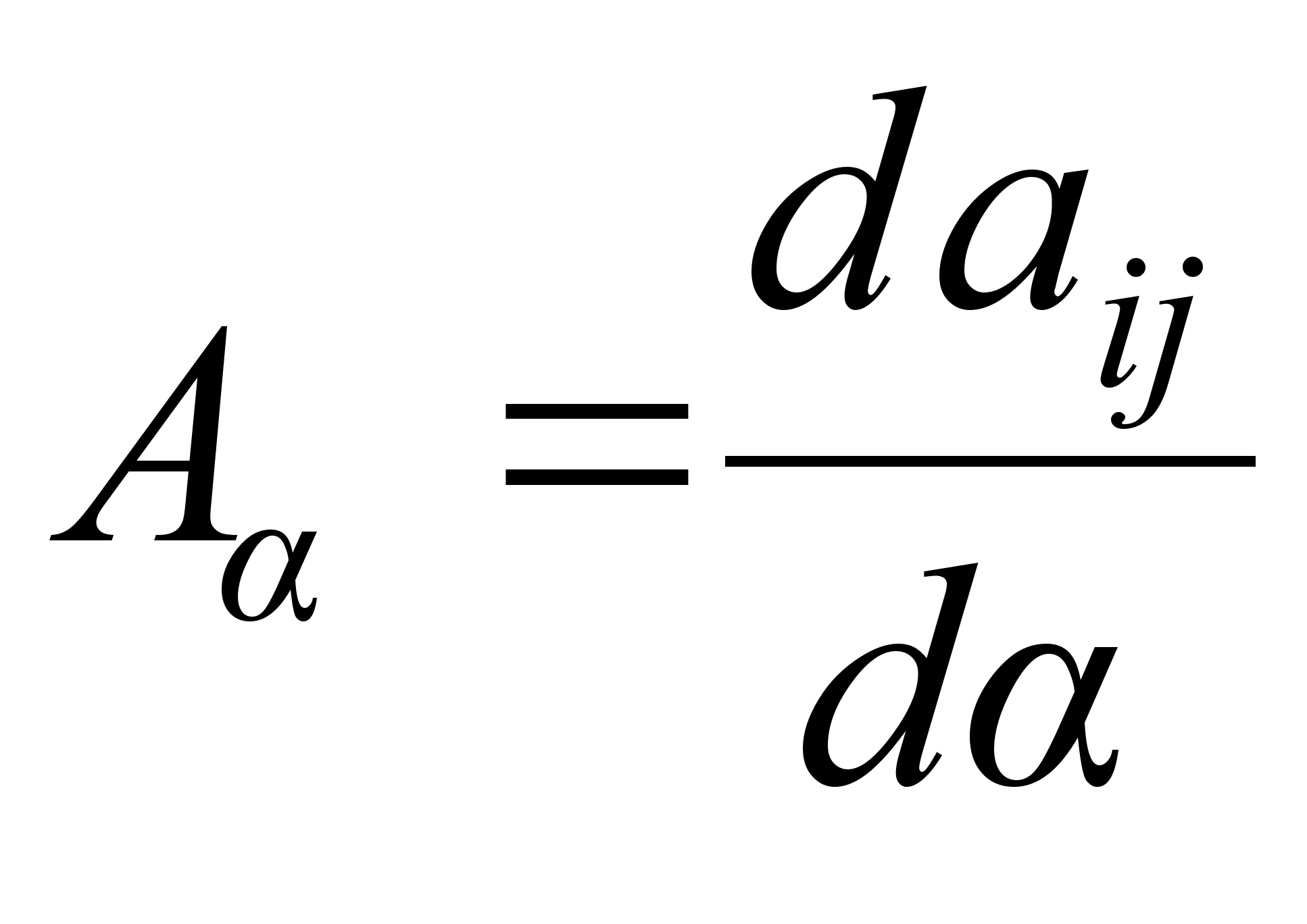, мы хотим определить матрицу . Явно прослеживается обобщение на случай ККИФ - преобразований и параметр заменяется вектором . Вдобавок, мы потребуем, чтобы и, следовательно, были квадратными и невырожденными.

Для более полного представления ситуации, вначале остановимся на достаточно очевидном решении этой проблемы, однако, которое может вызвать определенные вычислительные трудности и, поэтому, не рекомендуется. Данный подход основан на использовании (2.4.1) и решении следующего уравнения:

,

далее прямое дифференцирование дает:

(2.4.2)

Используя тот факт, что и, следовательно, - верхнетреугольные, (2.4.2) может быть использовано для вычисления элементов . Для этого применяется алгоритм прямой подстановки, который является стандартным алгоритмом решения линейных систем. Вычислительные сложности могут возникнуть, когда матрица и, следовательно, плохо обусловлены (т.е. почти вырождены). Алгоритм прямой подстановки в этом случае может давать, мягко говоря, неточные результаты.

Выбранный метод базируется на том наблюдении, что если матрица - ортогональная, то выполняется следующее равенство: . Дифференцируя это уравнение, находим, что

или (2.4.3)

Матрица , которая удовлетворяет соотношению - кососимметричная. Очевидно, что такая матрица имеет следующий вид: , где - строго нижнетреугольная. Поэтому (2.4.3) можно переписать в следующем виде:

(2.4.4)

для некоторой нижнетреугольной матрицы .

Лемма: Нижнетреугольная матрица в соотношении (2.26), где удовлетворяет

(2.4.1), причем - невырождена, является нижнетреугольной частью матрицы , причем

(2.4.5),

где соответственно нижнетреугольная, диагональная и верхнетреугольная матрицы и удовлетворяет (2.4.4).

Доказательство:

Продифференцировав равенство (2.4.1), получаем:

(2.4.6)

из которого имеем:

Используя тот факт, что

получаем, что

(2.4.7)

Далее, так как и верхнетреугольные матрицы, то и и также верхнетреугольные. Поэтому, нижнетреугольная часть должна в точности соответствовать нижнетреугольной части с обратным знаком. Следовательно, если , то

Уравнение (2.4.7) дает метод для вычисления . Подстановкой (2.4.5) и (2.4.4) в (2.4.7) получаем, что

(2.4.8)

и, таким образом, имеем

Тем самым получаем путь нахождения:

вычислить ;

привести к виду ;

вычислить

и результатом будет .

Уравнение (2.4.8) показывает всю опасность применения (2.4.6) непосредственно. Из соотношения (2.4.8) находим:

Первым слагаемым является , а вторым - . Записанное в таком виде соотношение (2.4.8), включает и в первое, и во второе слагаемое матрицу , но с разными знаками. Более того, матрица полная, то есть исключение происходит по всей матрице . Если значение матрицы небольшие, в сравнении с элементами матриц и , тогда сумма вычисляется достаточно точно. Однако если некоторые из элементов велики, тогда соответствующие элементы суммы будут неточны вследствие большого исключения элементов и результат в целом будет неточен.