Навигация
Проверка статистической гипотезы об адекватности модели задачи регрессии
2.2 Проверка статистической гипотезы об адекватности модели задачи регрессии.
Имеется выборка объёма n экспериментальных значений (xi;Ui). Предполагаем, что ошибки измерения xi пренебрежимо малы, а случайные ошибки измерения температур Ui подчинены нормальному закону с постоянной дисперсией s2. Мы выбрали функцию регрессии в виде:
Выясним, нельзя ли было ограничиться многочленом второго порядка, т.е. функцией вида:
(2.5)
C помощью МНК можно найти оценки этих функций и несмещённый оценки дисперсии отдельного измерения Ui для этих случаев:
Где r1 = 4 (количество точек – 6, параметра – 2).
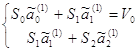 |
Нормальная система уравнений для определения новых оценок коэффициентов функции (2.5)с помощью МНК имеет вид:
(2.7)
Решая эту систему методом Гаусса, получим:
(2.8)
Чем лучше функция регрессии описывает эксперимент, тем меньше для неё должна быть оценка дисперсии отдельного измерения Ui, т.к. при плохом выборе функции в дисперсию войдут связанные с этим выбором дополнительные погрешности. Поэтому для того, чтобы сделать выбор между функциями U(x) и U(1)(x) нужно проверить значимость различия между соответствующими оценками дисперсии, т.е. проверить гипотезу:
Н0 – альтернативная гипотеза
Т.е. проверить, значимо ли уменьшение дисперсии при увеличении степени многочлена.
В качестве статического критерия рассмотрим случайную величину, равную:
(2.9)
имеющую распределение Фишера с(r ; r1) степенями свободы. Выбираем уровень распределения Фишера, находим критическое значение F*a, удовлетворяющее равенству: p(F>F*a)=a
В нашем случае F=349.02, а F*a=10,13.
Если бы выполнилось практически невозможное соотношение F>Fa, имевшее вероятность 0,01, то гипотезу Н0 пришлось бы отклонить. Но в нашем случае можно ограничиться многочленом
, коэффициенты в котором неодинаковы.
3. Нахождение коэффициента теплопроводности a.
 |
Коэффициент a вычислим по формуле (1.5), обозначим:
(3.1)
Определим допустимую абсолютную погрешность величины интеграла I, исходя из требования, чтобы относительная погрешность вычисления a не превосходила 0,1%, т.е.:
(3.2)
Т.к. из (3.1) очевидно, что a>a0, то условие (3.2) заведомо будет выполнено, если:
(3.3)
Т.е. в качестве предельно допустимой абсолютной погрешности вычисления интеграла I возьмём d=0,001Т (3.4)
Т=218 оС, следовательно, d=0,218 оС.
Похожие работы
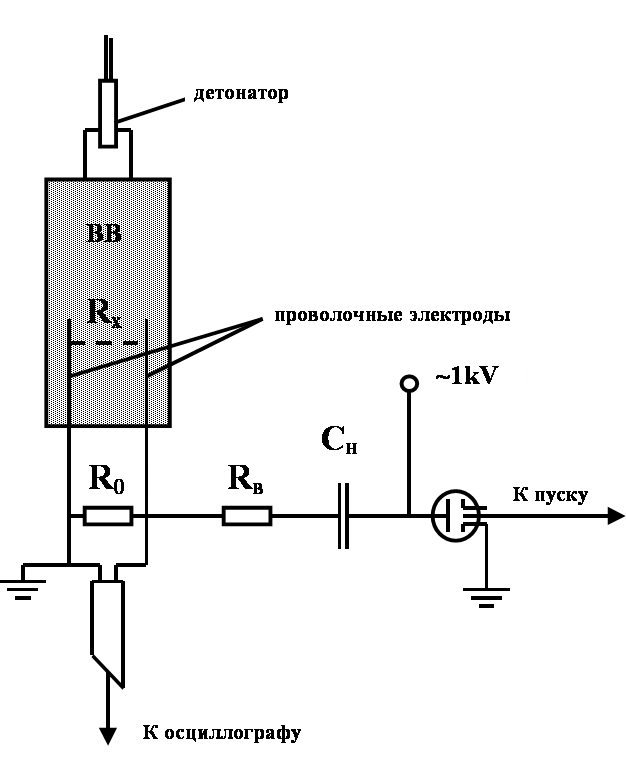
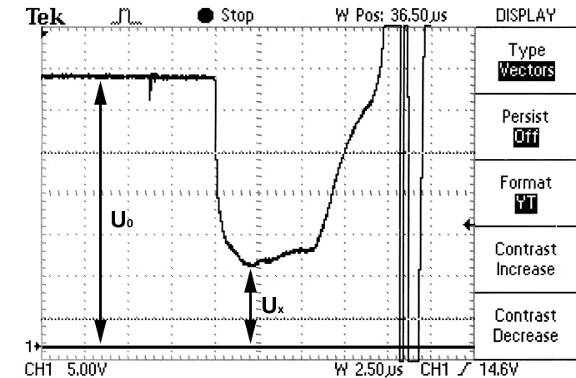
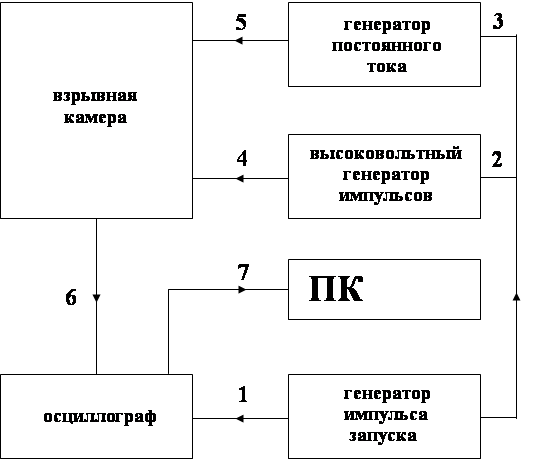
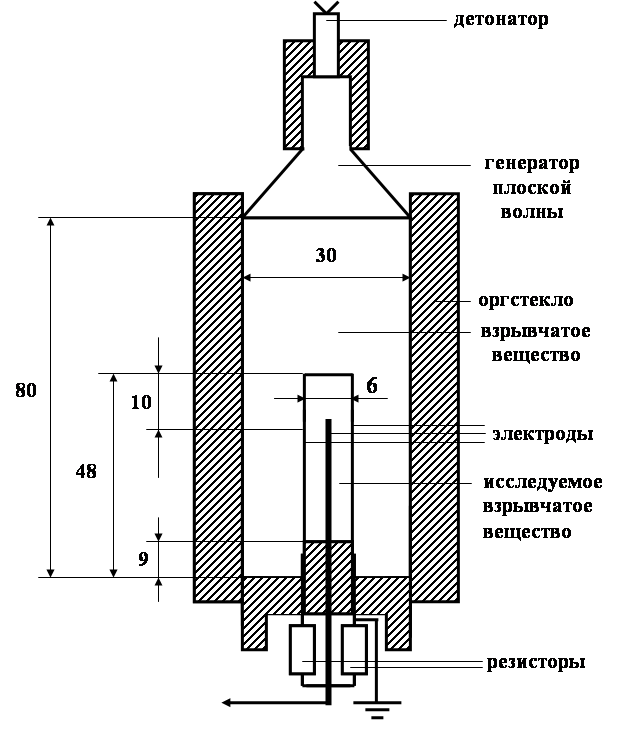
... Автору дипломной работы было предложено продолжить исследования электропроводности продуктов детонации. Основной задачей являлось перейти к изучению распределения электропроводности конденсированных взрывчатых веществ за фронтом пересжатой детонации. Объектом исследования выбраны такие взрывчатые вещества как октоген, гексоген, тэн и тотил. Цель исследований – получить информацию, способную ...
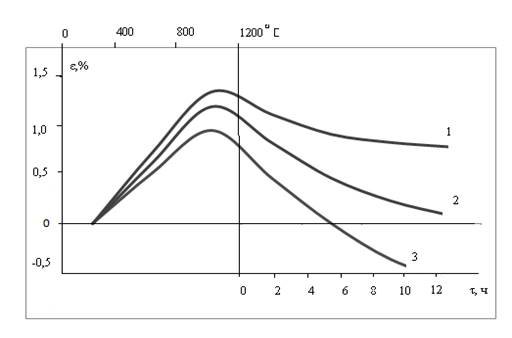
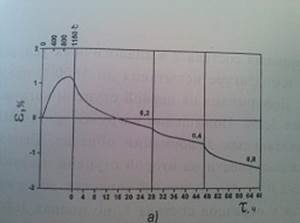
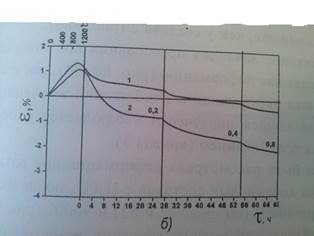
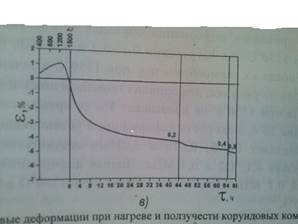
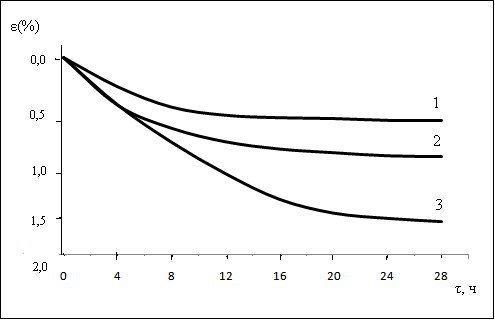
... в его средней части. Таким образом, можно считать, что распределение температуры в образце является достаточно равномерным, а это свидетельствует о равномерности температуры в центральной зоне самой печи. 2.2 Исследование деформации и ползучести керамических материалов 2.2.1 Керамических материалов трубчатых изделий Деформация при нагреве. С целью установления предельной температуры эксплуатации ...
... свариваемого металла, конструкцией сварного соединения, режимом сварки и начальной температурой изделия. Рекомендуется подогрев и последующая термообработка. Способы сварки: РД, РАД, АФ, КТ. 2. Исследование процессов взаимодействия между металлом, газом и шлаком 2.1 Характеристика защиты металла от взаимодействия с окружающей средой Сварка плавлением - высокотемпературный процесс, ...
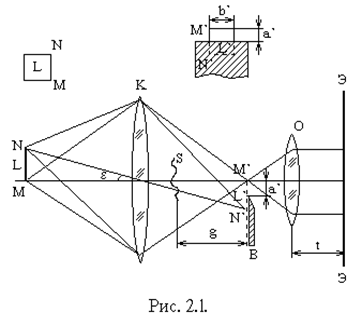
... неоднородность имеет значительную глубину. Прибор интерференционно-теневой ИАБ-458 Прибор интерференционно-теневой ИАБ-458 предназначен для качественных и количественных исследований теневым методом неоднородностей оптически прозрачных сред. В приборе реализуются следующие методы исследования: светящейся точки, щели и ножа, щели и нити, сдвиговой интерферометрии и голографии. На рис. 2.4 ...

0 комментариев