Навигация
Решение уравнения комбинированным методом
4.1 Решение уравнения комбинированным методом
Время установления режима определяется по формулам (1.6) и (1.7).
Проведём сначала отделение корней. Имеем y = ctg(x) и y = Ax. Приведём уравнение к виду: A x sin(x)-cos(x) = 0. Проведём процесс отделения корня.
| F(x) | -1 | -0.6285 | 0.4843 |
| x | 0.01 | 0.05 | 0.1 |
т.е. x с [0.01;0.05]
Убедимся, что корень действительно существует и является единственным на выбранном интервале изоляции.
f(a) f(b)<0 – условие существования корня выполняется
f’(x) на [a;b] – знакопостоянна: f’(x)>0 – условие единственности также выполняется. Проведём уточнение с погрешностью не превышающей e=10-4
Строим касательные с того конца, где f(x) f”(x)>0
f”(x)=(2A+1)cos(x) – A x sin(x). f”(x)>0 на (a;b), следовательно касательные строим справа, а хорды слева. Приближение корня по методу касательных:
по методу хорд:
Вычисление ведём до того момента, пока не выполнится условие:
Результаты вычислений заносим в таблицу:
| n | an | bn | f(an) | f(bn) |
| 0 | 0.05 | 0.1 | -0.6285 | 0.4843 |
| 1 | 0.07824 | 0.08366 | -0.0908 | 0.0394 |
| 2 | 0.08202 | 0.08207 | -9.1515 10-4 | 3.7121 10-4 |
| 3 | 0.08206 | 0.08206 | -8.4666 10-8 | 3.4321 10-8 |
Т0 = 72,7176 секунд.
4.2 Решение уравнения комбинированным методом
Приведём f(x) = 0 к виду x = j(x). Для этого умножим обе части на произвольное число m, неравное нулю, и добавим к обеим частям х:
X = x - m f(x)
j(x) = x - m A x sin(x) + m cos(x)
В качестве m возьмём:
где М = max [f’(x)] на [a;b], а m = min [f’(x)] на [a’b]
В силу монотонности f’(x) на [a;b] имеем m = f’(а), М = f’(b). Тогда m = 0,045.
Приближение к корню ищем по следующей схеме:
Вычисление ведём до тех пор, пока не выполнится условие:
(q = max |j’(x)| на [a’b])
j’(x) на [a’b] монотонно убывает, поэтому максимум его модуля достигается на одном из концов.
j’(0,05) = 0,3322 j’(0,1) = -0,3322, следовательно, q = 0.3322 < 1. В этом случае выполняется условие сходимости и получается последовательность:
| i | xi | j( xi) | D xi |
| 0 | 0.075 | 0.082392 | 0.00739 |
| 1 | 0.082392 | 0.082025 | 0.000367 |
| 2 | 0.082025 | 0.08206 | 3.54 10-5 |
| 3 | 0.08206 | 0.082057 | 3.33 10-6 |
| 4 | 0.082057 | 0.082057 | 3.15 10-7 |
Итак, с погрешностью, меньшей 10-4, имеем:
Т0 = 72,7176 с. , x = 0.03142
Похожие работы
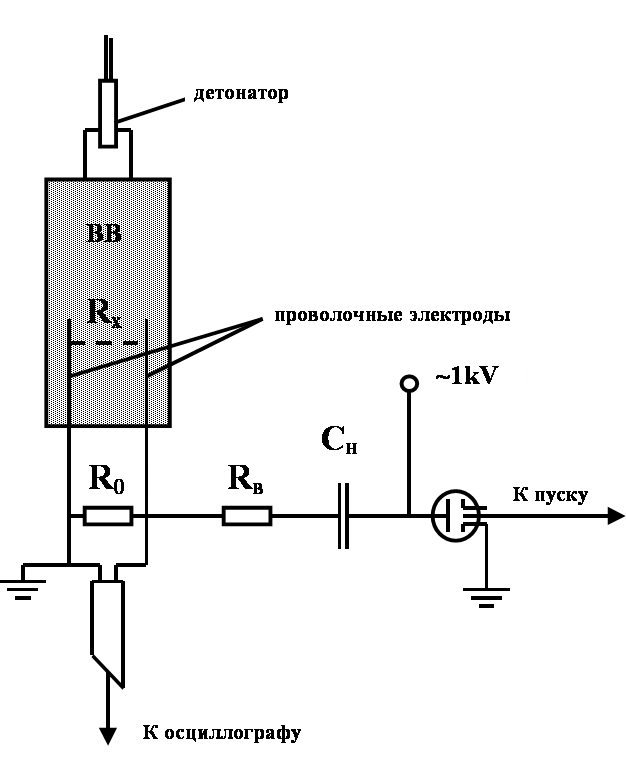
... Автору дипломной работы было предложено продолжить исследования электропроводности продуктов детонации. Основной задачей являлось перейти к изучению распределения электропроводности конденсированных взрывчатых веществ за фронтом пересжатой детонации. Объектом исследования выбраны такие взрывчатые вещества как октоген, гексоген, тэн и тотил. Цель исследований – получить информацию, способную ...
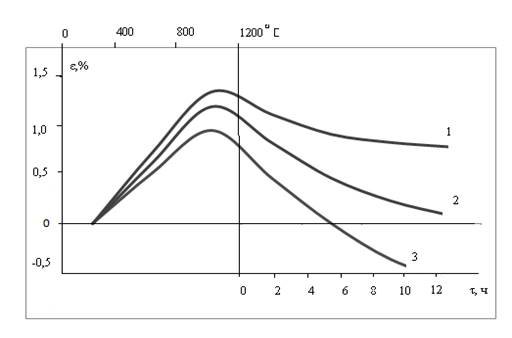
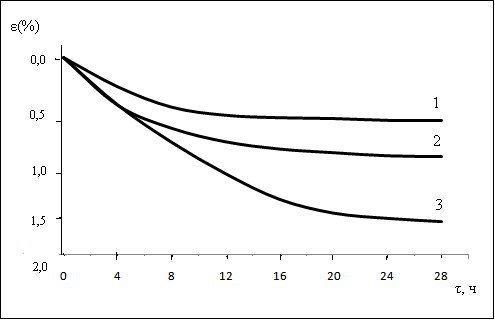
... в его средней части. Таким образом, можно считать, что распределение температуры в образце является достаточно равномерным, а это свидетельствует о равномерности температуры в центральной зоне самой печи. 2.2 Исследование деформации и ползучести керамических материалов 2.2.1 Керамических материалов трубчатых изделий Деформация при нагреве. С целью установления предельной температуры эксплуатации ...
... свариваемого металла, конструкцией сварного соединения, режимом сварки и начальной температурой изделия. Рекомендуется подогрев и последующая термообработка. Способы сварки: РД, РАД, АФ, КТ. 2. Исследование процессов взаимодействия между металлом, газом и шлаком 2.1 Характеристика защиты металла от взаимодействия с окружающей средой Сварка плавлением - высокотемпературный процесс, ...
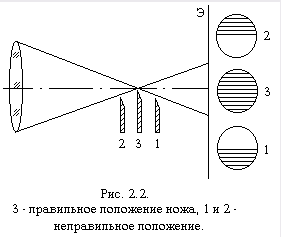
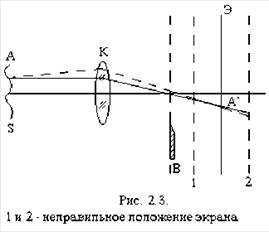
... неоднородность имеет значительную глубину. Прибор интерференционно-теневой ИАБ-458 Прибор интерференционно-теневой ИАБ-458 предназначен для качественных и количественных исследований теневым методом неоднородностей оптически прозрачных сред. В приборе реализуются следующие методы исследования: светящейся точки, щели и ножа, щели и нити, сдвиговой интерферометрии и голографии. На рис. 2.4 ...

0 комментариев