Навигация
5. Решение краевой задачи
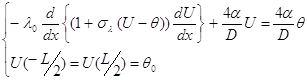 |
Используем метод малого параметра. Краевую задачу запишем в виде:
(5.1)
Введя новую переменную y = (U - q0)/(q - q0), запишем (5.1) в виде:
(5.2)
e = sl(q - q0) =0.18, L/2 =0.0193. В качестве малого параметра возьмём e.
Тогда, подставив y(x) в уравнение (5.2) и перегруппировав члены при одинаковых степенях e, получим:
(5.3)
Ограничимся двумя первыми членами ряда:
Из (5.2) и (5.3) находим общее решение уравнения для y0:
где y0 с тильдой – частное решение данного неоднородного уравнения; y(1) и y(2) – линейно независимые решения однородного уравнения.
Корни уравнения:
y0общ = 1 + c1ch(px)+c2sh(px), где p = 0.01953
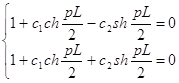 |
Константы найдём из граничных условий:
откуда с1 = 0, с2 = -0,57; т.е. имеем функцию:
y0 = 1 - 0.57 sh(px)
Общее решение:
Частное решение:
Дифференцируя и подставляя в уравнение, получим:
А1 = 0; А2 = -0,1083; В1 = 0; В2 = 17,1569;
Тогда общее решение для y1 имеет вид:
с3 = 0; с4 = 0,0462
Перейдя к старой переменной U, получим:
q0 = 0; q1 = -374.11; q2 = -12.9863; q3 = 2057
Итоговое уравнение:
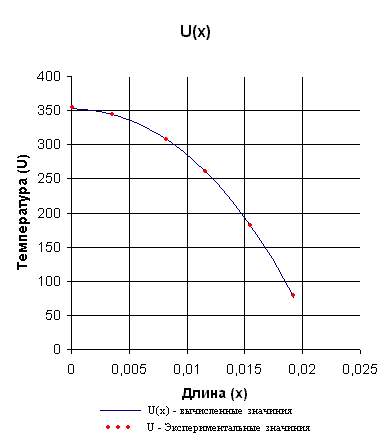
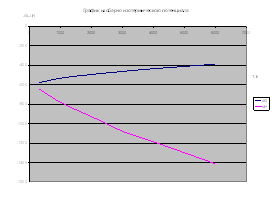
Пользуясь этой формулой, составим таблицу значений функции U(x):
| x | U(x) | U |
| 0 | 352.9075 | 353 |
| 0.0019 | 350.4901 | |
| 0.0039 | 343.1972 | 343 |
| 0.0058 | 330.9053 | |
| 0.0077 | 313.4042 | 313 |
| 0.0097 | 290.391 | |
| 0.0116 | 261.4598 | 261 |
| 0.0135 | 226.0893 | |
| 0.0154 | 1836255 | 184 |
| 0.0174 | 133.2579 | |
| 0.0193 | 74 | 74 |
Используя данную таблицу, строим график функции U(x).
[см. приложение 1]
6. Заключение
Решение задачи на ЭВМ при помощи вычислительной системы ManhCad 7.0 дало результаты (функцию распределения температуры в тонком цилиндрическом стержне), полученные по решению практического задания и обработкой эксперимента (функции регрессии), которые практически (в пределах погрешности) совпадают с экспериментальными значениями.
Литература1. Методические указания «Методы приближённых вычислений. Решение нелинейных уравнений»
(ЛТИ им. Ленсовета, Л. 1983)
2.Методические указания «Приближённые методы ислисления определённых интегралов»
(ЛТИ им. Ленсовета, Л. 1986)
3. Методические указания «Изучение распределения температуры в тонком цилиндрическом стержне»
(ЛТИ им. Ленсовета, Л. 1988)
 |
Приложение 1
Похожие работы
... Автору дипломной работы было предложено продолжить исследования электропроводности продуктов детонации. Основной задачей являлось перейти к изучению распределения электропроводности конденсированных взрывчатых веществ за фронтом пересжатой детонации. Объектом исследования выбраны такие взрывчатые вещества как октоген, гексоген, тэн и тотил. Цель исследований – получить информацию, способную ...
... в его средней части. Таким образом, можно считать, что распределение температуры в образце является достаточно равномерным, а это свидетельствует о равномерности температуры в центральной зоне самой печи. 2.2 Исследование деформации и ползучести керамических материалов 2.2.1 Керамических материалов трубчатых изделий Деформация при нагреве. С целью установления предельной температуры эксплуатации ...
... свариваемого металла, конструкцией сварного соединения, режимом сварки и начальной температурой изделия. Рекомендуется подогрев и последующая термообработка. Способы сварки: РД, РАД, АФ, КТ. 2. Исследование процессов взаимодействия между металлом, газом и шлаком 2.1 Характеристика защиты металла от взаимодействия с окружающей средой Сварка плавлением - высокотемпературный процесс, ...
... неоднородность имеет значительную глубину. Прибор интерференционно-теневой ИАБ-458 Прибор интерференционно-теневой ИАБ-458 предназначен для качественных и количественных исследований теневым методом неоднородностей оптически прозрачных сред. В приборе реализуются следующие методы исследования: светящейся точки, щели и ножа, щели и нити, сдвиговой интерферометрии и голографии. На рис. 2.4 ...

0 комментариев