Лабораторные работы по Основам теории систем

Телешовой Елизаветы, гр. 726,

Цель работы: Решение задач линейного программирования симплекс-методом. Варианты разрешимости задач линейного программирования.

1 вариант.

1. Четыре студента: Иванов, Петров, Сидоров и Васильев пошли на концерт группы «Чайф», захватив пиво 2 сортов: «Русич» и «Премьер». Определить план распития напитков для получения максимального суммарного опьянения (в ). Исходные данные даны в таблице:

2. Математическая модель.

2.1 Управляемые параметры

x₁[л] – количество выпитого пива «Русич».

x₂[л] – количество выпитого пива «Премьер».

– решение.

2.2 Ограничения

– количество пива «Русич», выпитого Ивановым.

– количество пива «Премьер», выпитого Ивановым.

– общее количество пива, выпитого Ивановым.

Общее количество пива, выпитого Ивановым, не превосходит имеющихся у него запасов пива, поэтому:

(л).

Аналогично строим другие ограничения:

(л).

(л).

(л).

3. Постановка задачи.

Найти ^*, где достигается максимальное значение функции цели:

4. Решение.

при:

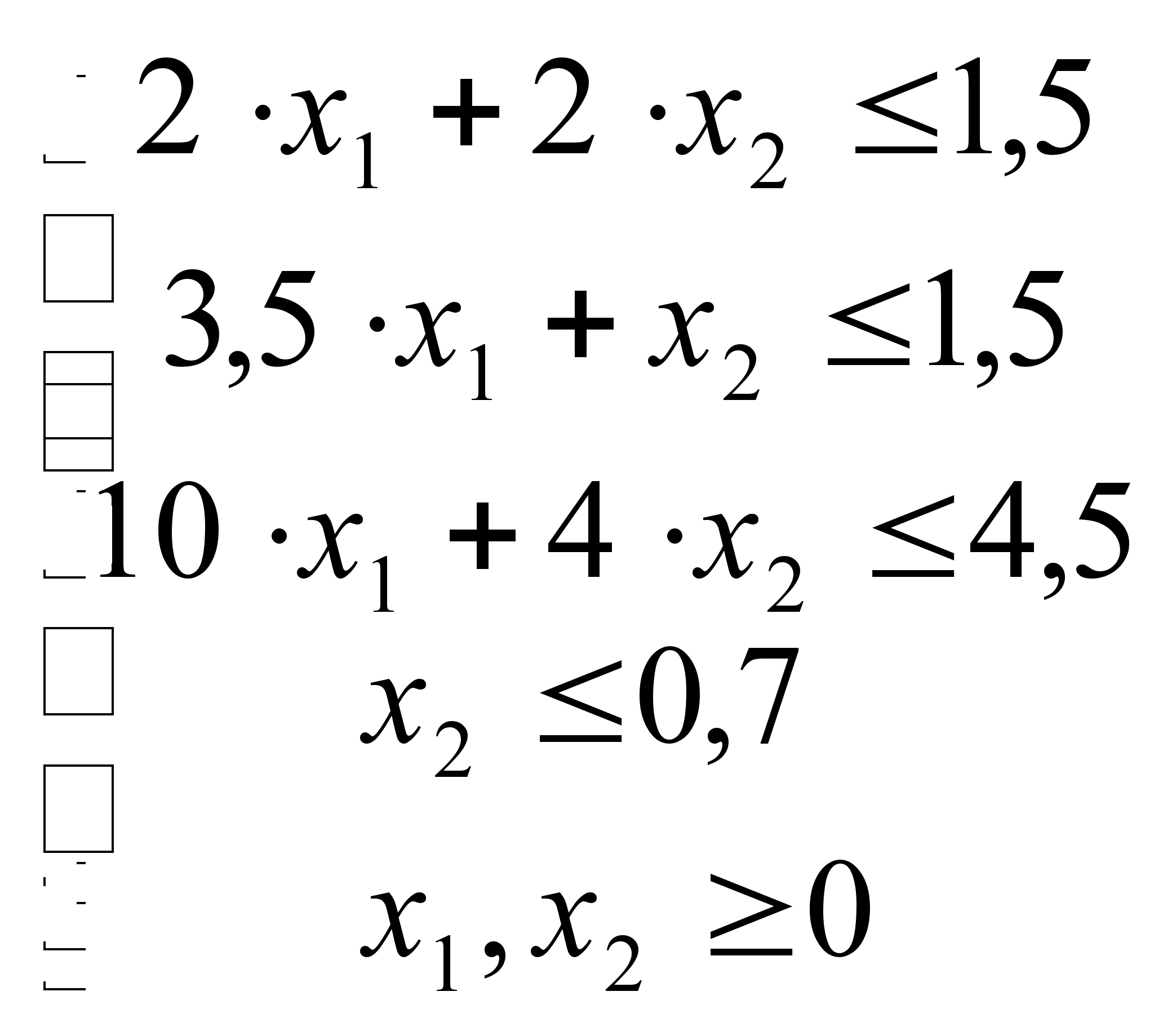
Приведем задачу к каноническому виду:

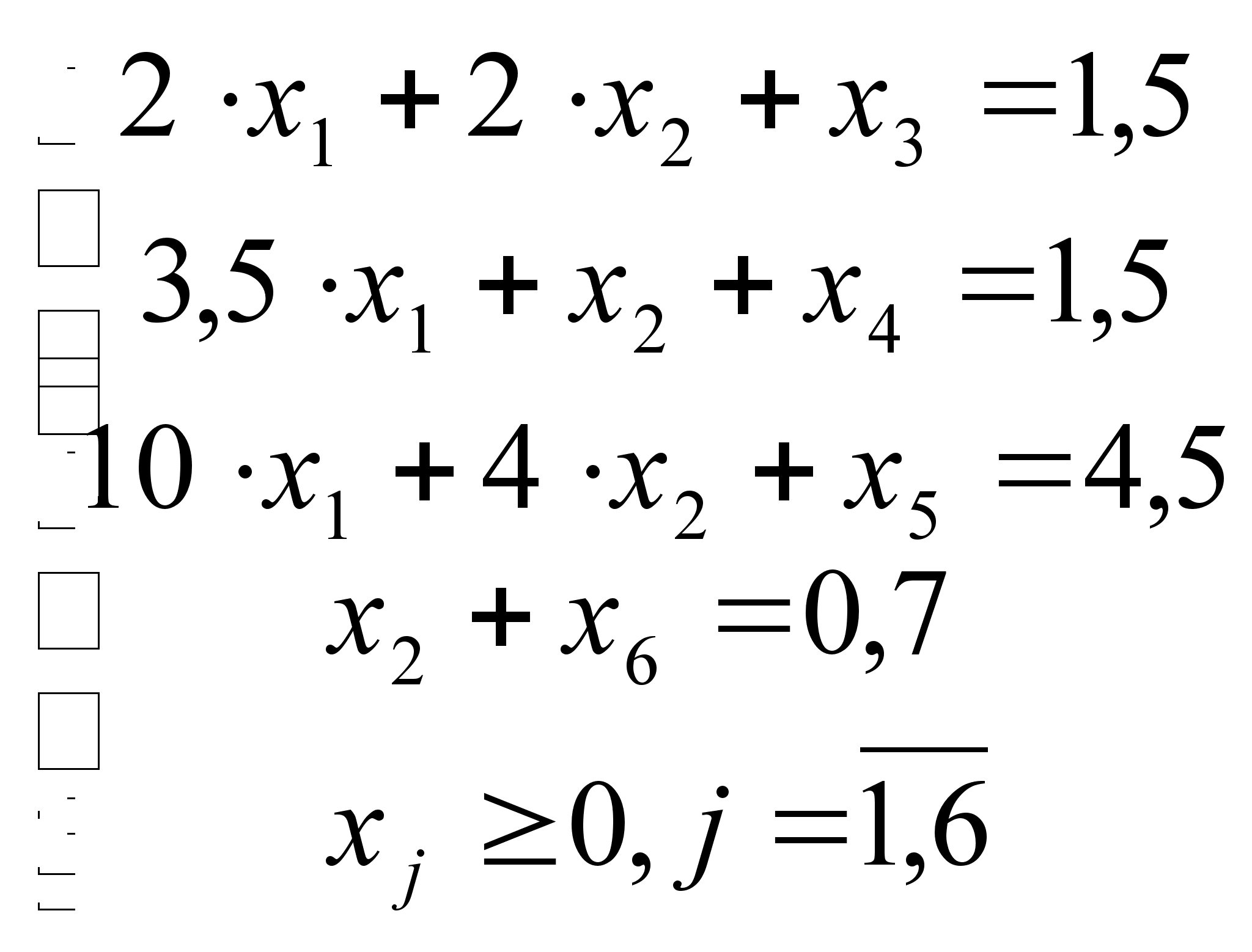
Определим начальный опорный план: .

Это решение является опорным, т.к. вектора условий при положительных компонентах решения линейно независимы, также , где , но не все оценки положительны (, где )

Опорный план является оптимальным, если для задачи максимизации все его оценки неотрицательны. не является оптимальным, значит критерий можно улучшить, если увеличить одну их отрицательных свободных переменных. Будем увеличивать , т.к. ее увеличение вызовет большее увеличение функции цели.

Предположим, что , тогда:

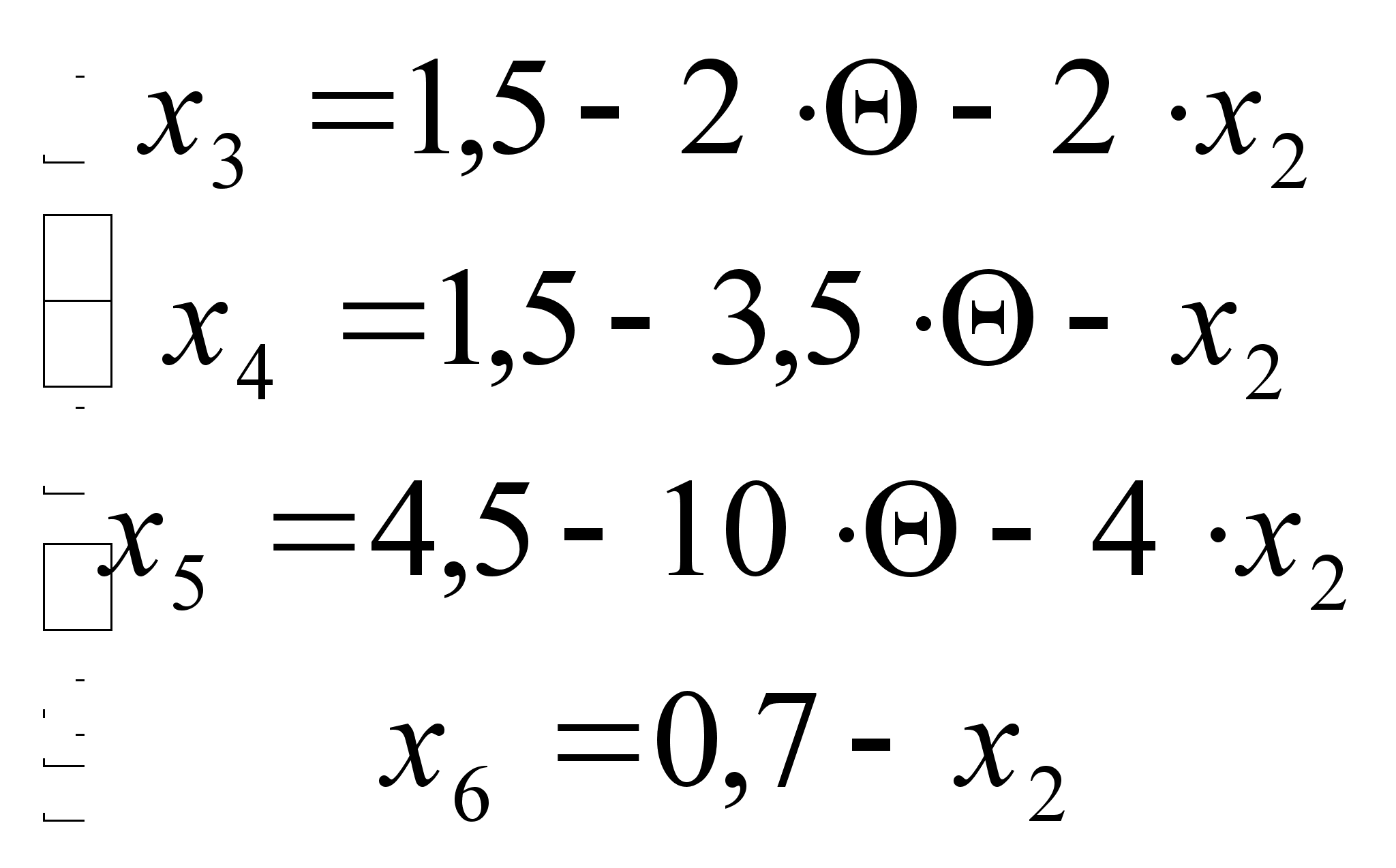
Запишем новый опорный план: . Все оценки опорного плана должны быть неотрицательны, а значит должны выполняться условия:

=>

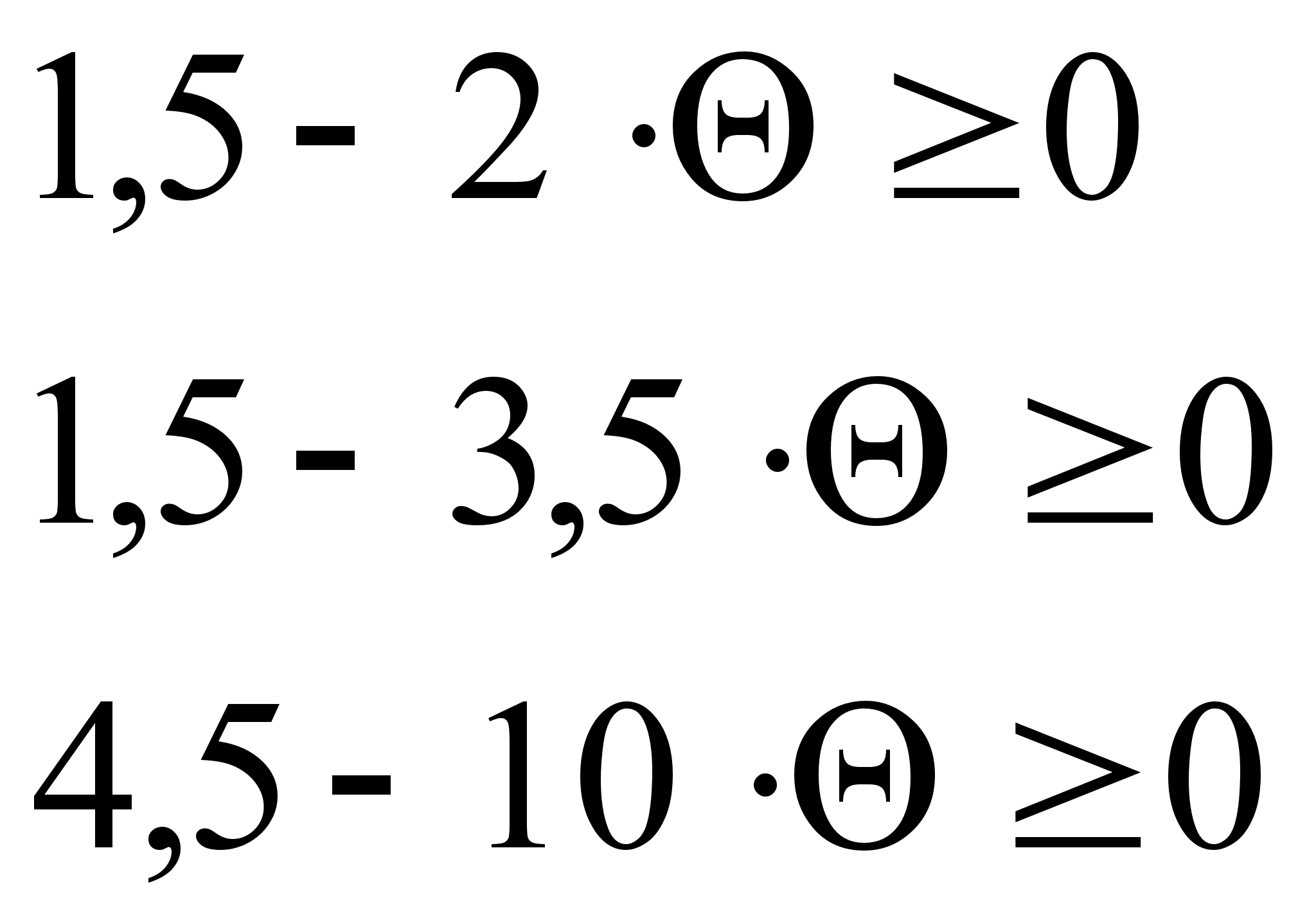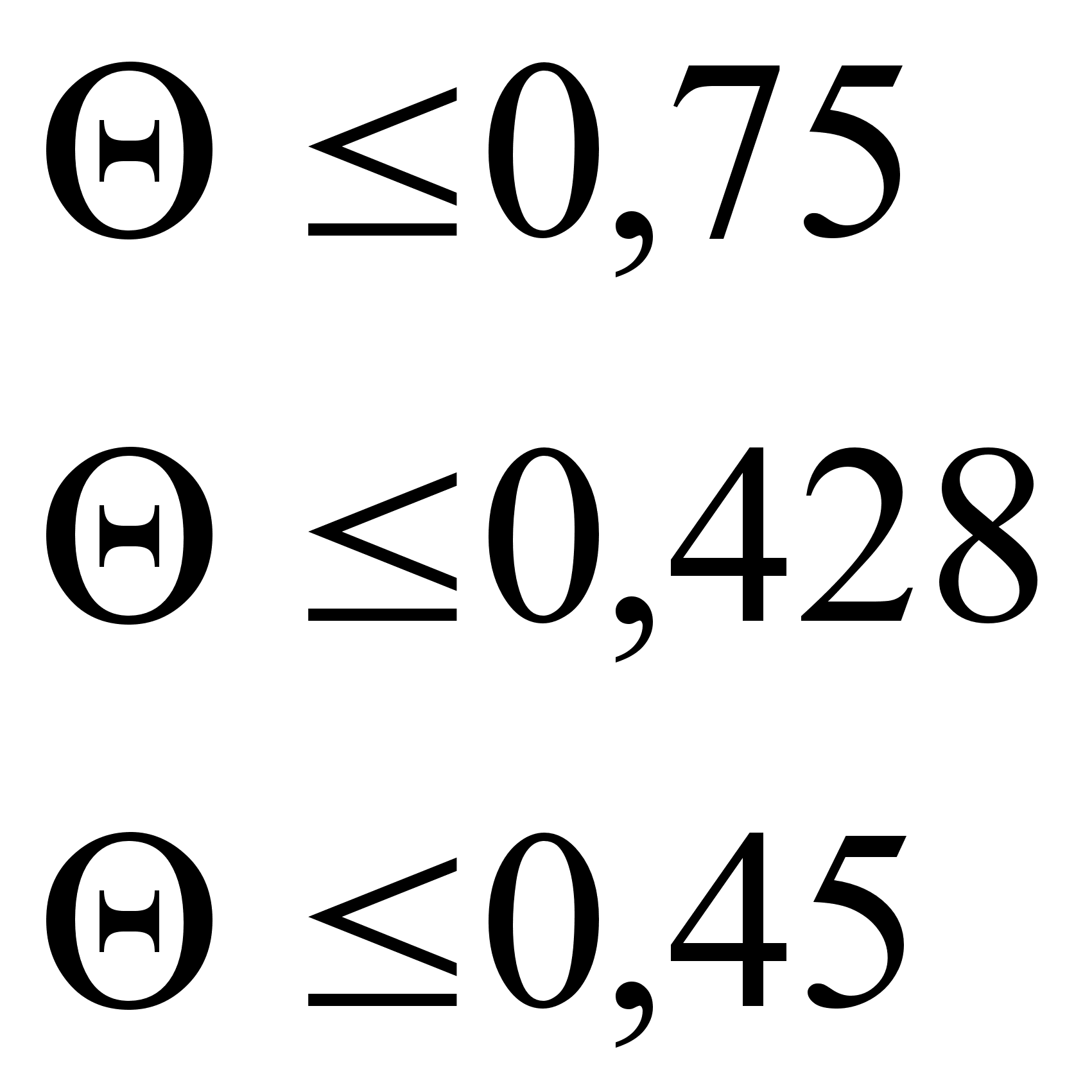
При увеличении , первой перестает выполнять условие неотрицательности переменная , т.к. она первая обращается в ноль. Значит выведем из базиса . Теперь базисными переменными являются , а свободными . Для анализа этого плана выразим функцию цели через новые переменные.

Из ограничения (2) имеем: .

Подставляя в функцию цели: получаем:

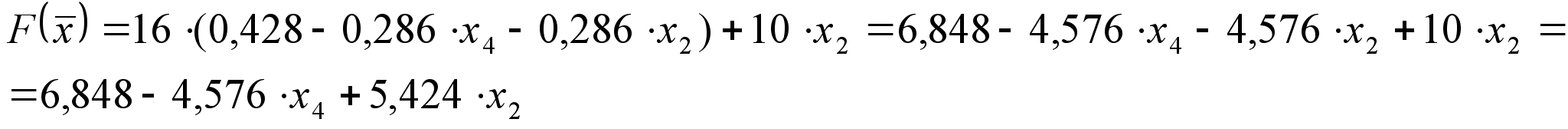
Оформим данный этап задачи в виде симплекс-таблицы:

Начальная симплекс-таблица:

;

Пересчитаем элементы исходной таблицы по правилу четырехугольника:

;

Пересчитав все оценки, видим, что , значит критерий можно улучшить. Будем увеличивать . Пусть , тогда:

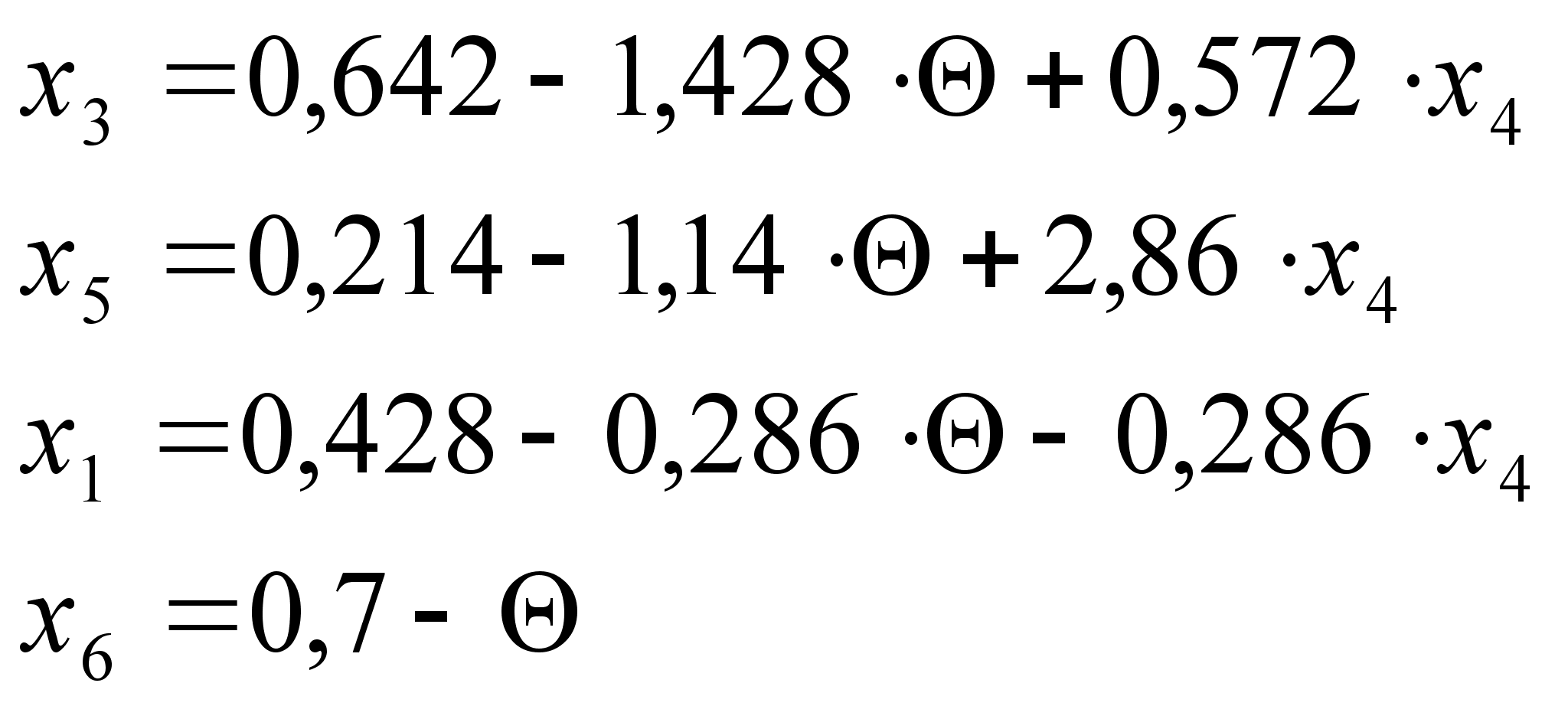
откуда получаем:

;

Все оценки опорного плана должны быть неотрицательны, а значит должны выполняться условия:

=>

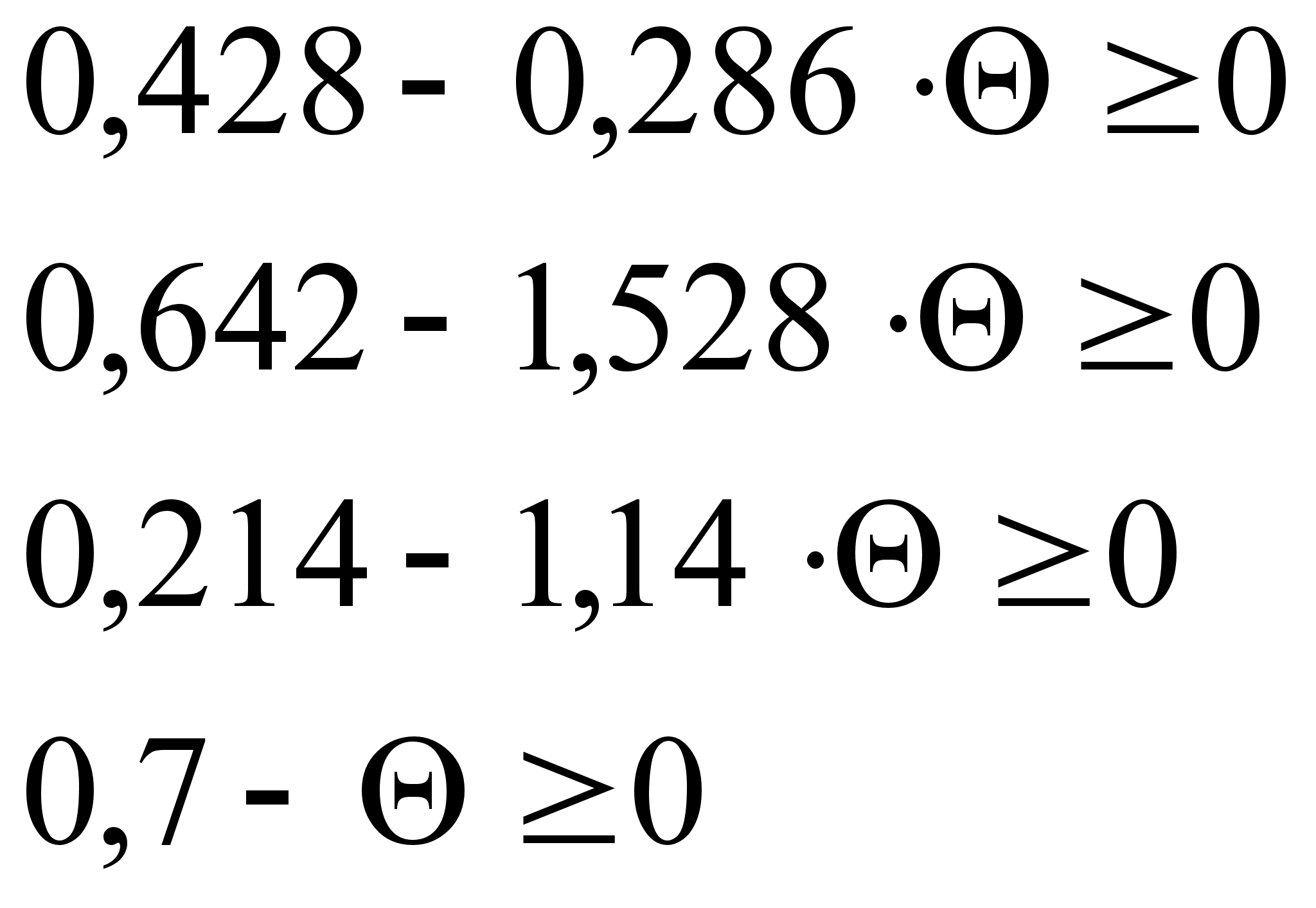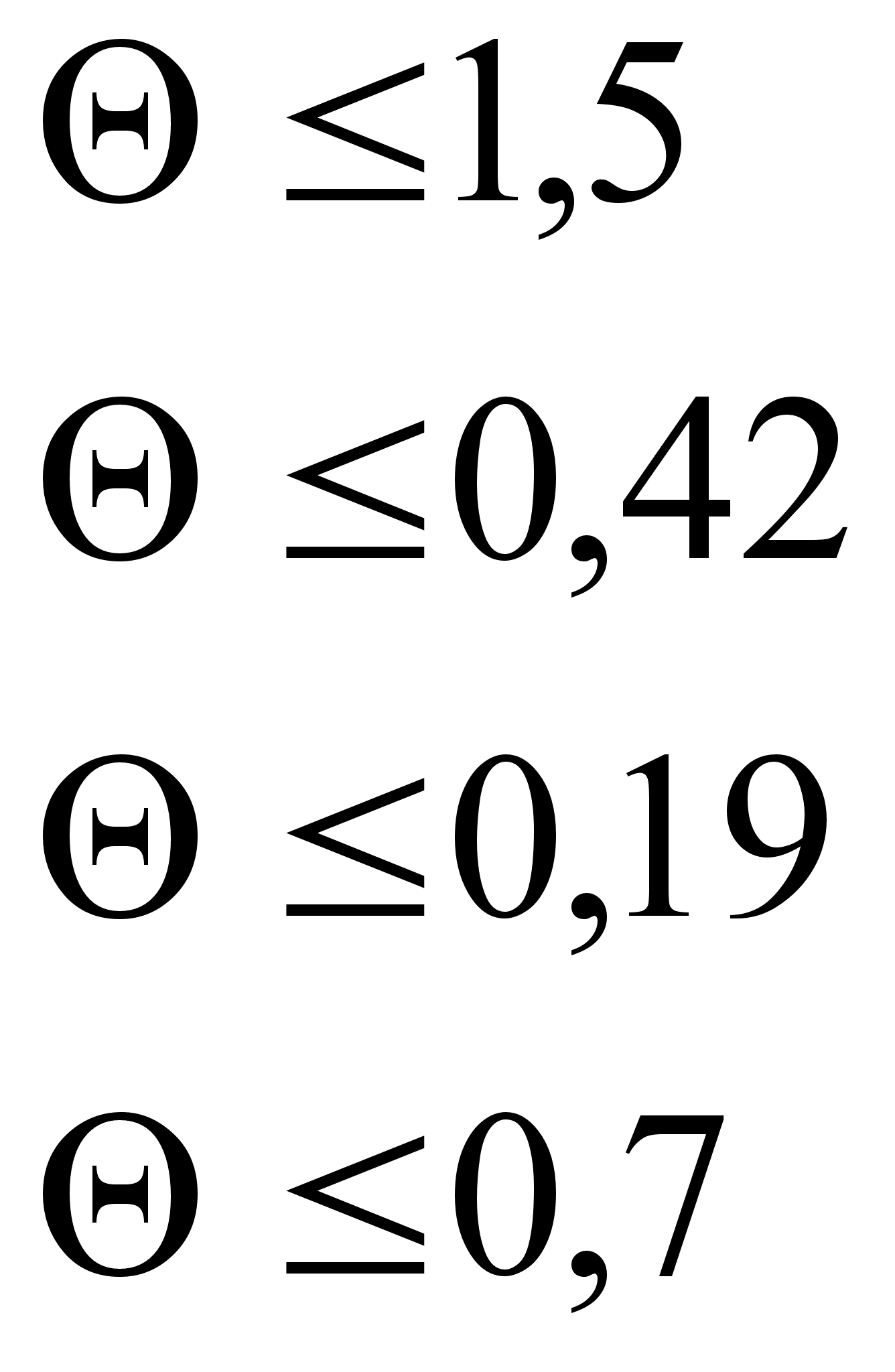
Выведем из базиса . Теперь базисными переменными являются , а свободными . Выразим функцию цели через новые переменные:

, а из ограничений (2) и (3): . Тогда: ;

Пересчитав все оценки, видим, что , значит критерий можно улучшить. Будем увеличивать . Пусть , тогда:

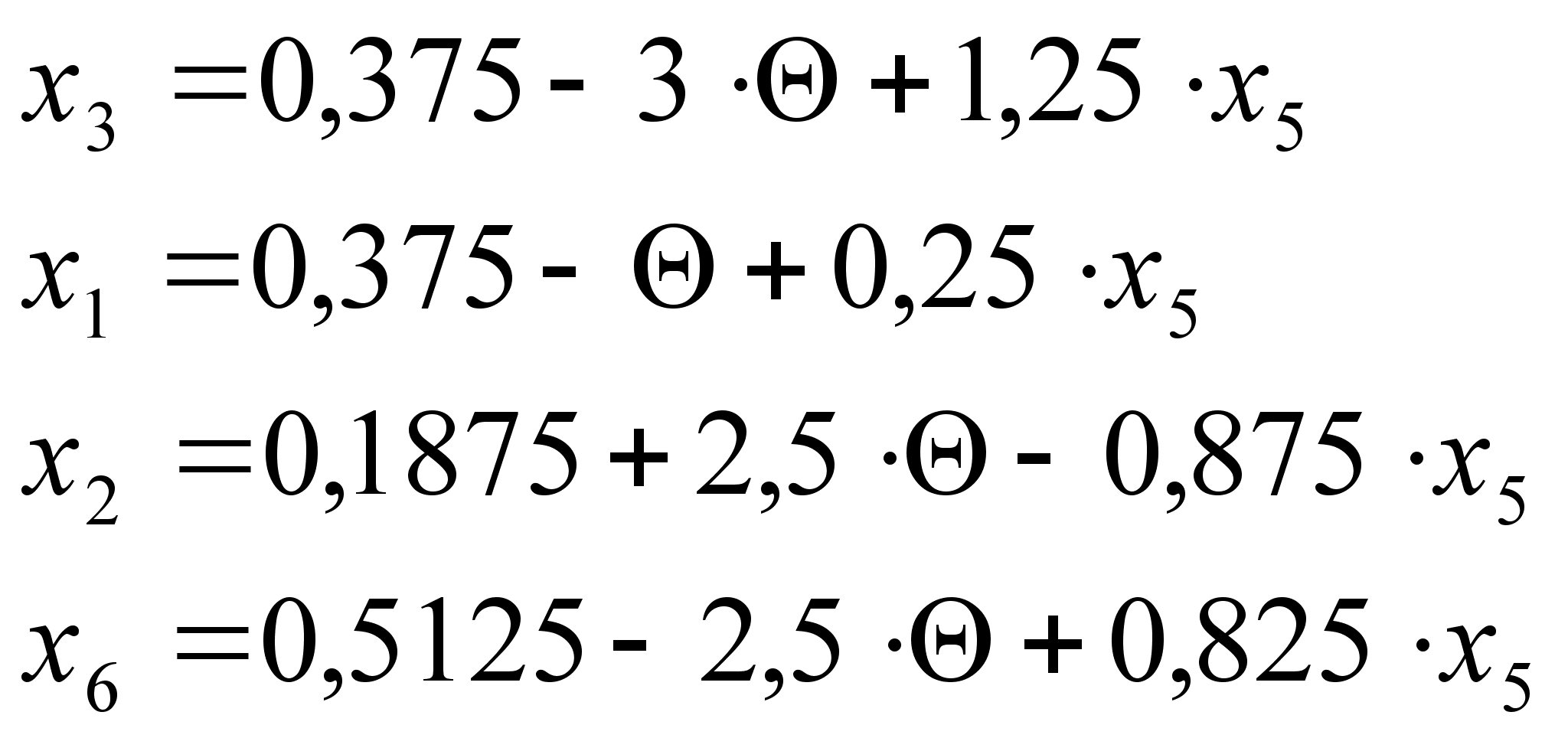
откуда получаем:

;

Все оценки опорного плана должны быть неотрицательны, а значит должны выполняться условия:

=>

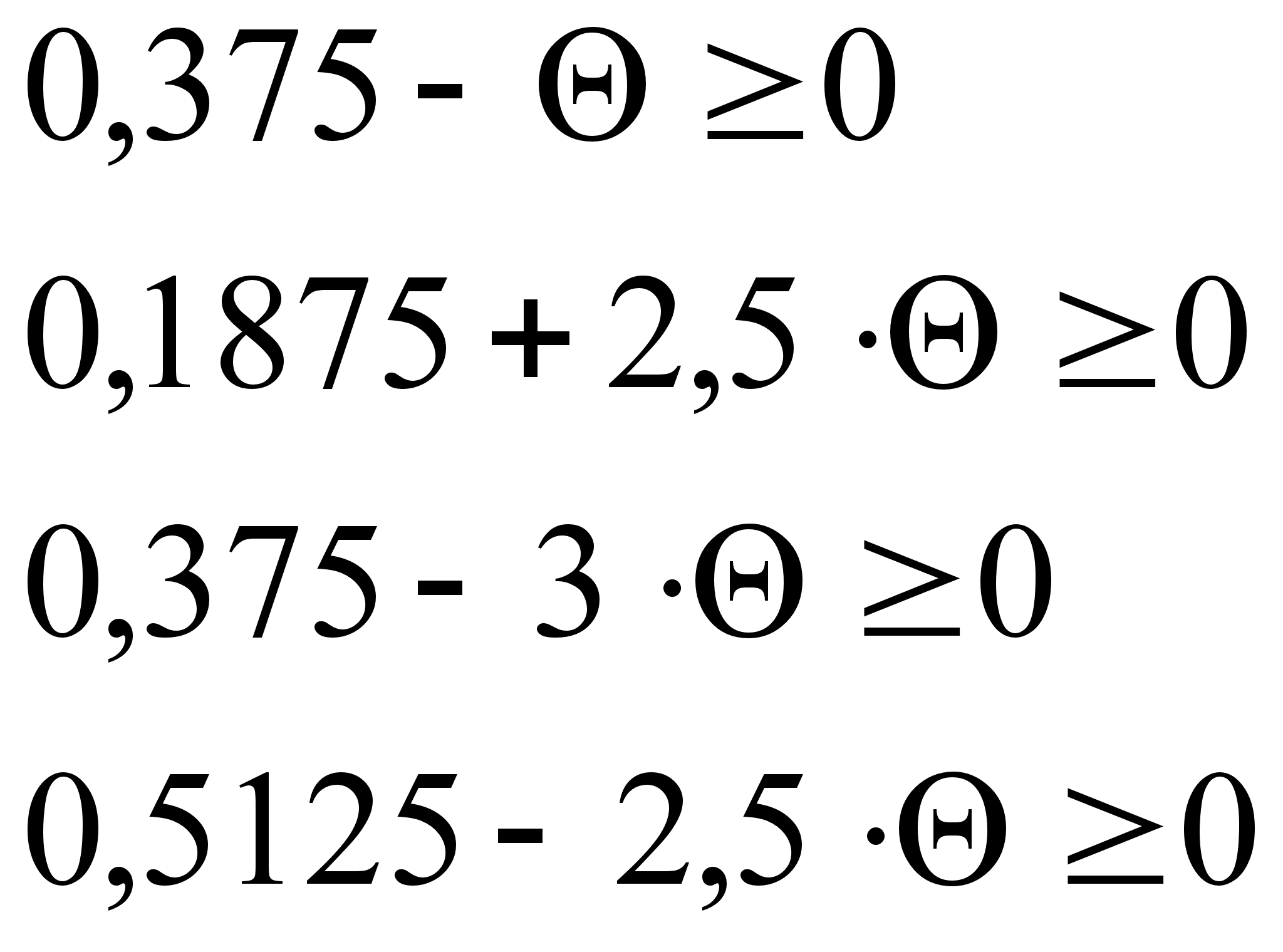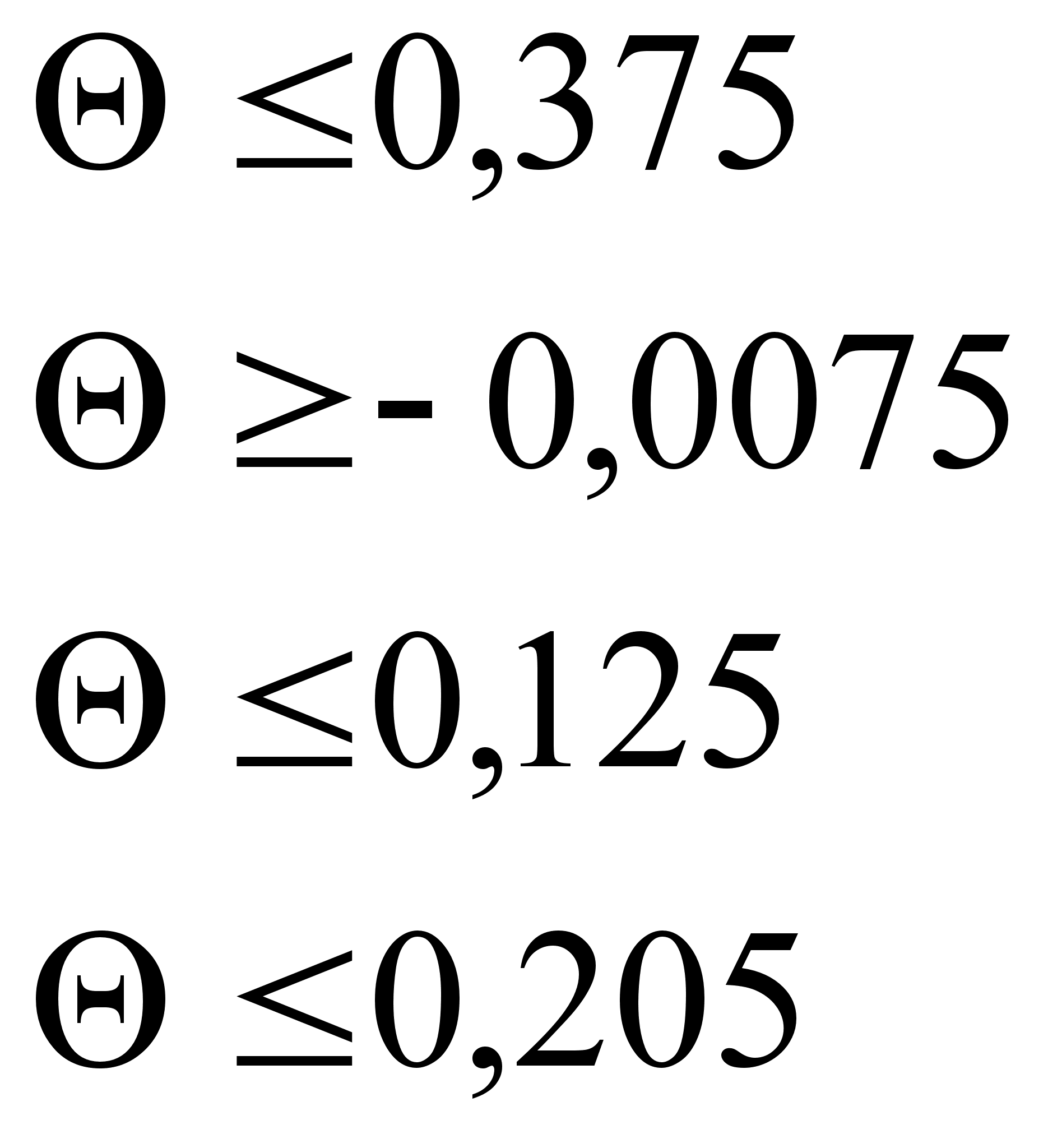
Выведем из базиса . Теперь базисными переменными являются , а свободными . Выразим функцию цели через новые переменные:

, а из ограничений (1) и (2): . Тогда: ;

Видим, что все оценки положительны, значит любое увеличение какой-либо свободной переменной уменьшит критерий. Данное решение является оптимальным. Изобразим это решение на графике:

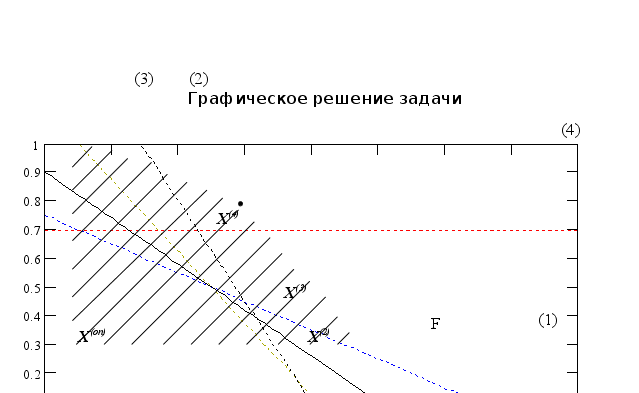
Видим, что единственное и достигается в угловой точке области допустимых решений.

Похожие работы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ (МЕХАНИКА И ТЕРМОДИНАМИКА)

Скачать

89077

4

25

... изменение. 3. Что такое термодинамическая вероятность состояния (статис­тический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...

Проблема формирования исследовательских умений при проведении лабораторных практикумов

Скачать

53740

0

0

... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...

Разработка виртуальной лабораторной работы на базе виртуальной асинхронной машины в среде MATLAB

Скачать

114601

5

73

... концентрических окружностей с уменьшающимся радиусом по мере затухания колебаний скорости и момента. Аналогичная картина наблюдается при ступенчатом набросе нагрузки. 5. РАЗРАБОТКА ВИРТУАЛЬНОЙ ЛАБОРАТОРНОЙ РАБОТЫ НА БАЗЕ ВИРТУАЛЬНОЙ АСИНХРОННОЙ МАШИНЫ   Иную возможность анализа АД представляет специализированный раздел по электротехнике Toolbox Power System Block. В его библиотеке имеются блоки ...

Проект лабораторного стенда по изучению частотного электропривода на базе автономного инвертора напряжения фирмы OMRON

Скачать

80734

7

0

... Р- 122”.- Техническое описание. 3 “Техника чтения схем автоматического управления и технологического контроля”. – Энергоатомиздат, 1991.4 ДОКЛАД “Проект лабораторного стенда по изучению частотного электропривода на базе автономного инвертора напряжения фирмы OMRON”. В настоящее время на АО “Северсталь” происходит активное внедрение частотных преобразователей. Это объясняется тем, что частотное ...