Навигация
Решение с помощью IBLP
72134
знака
54
таблицы
892
изображения
1. Решение с помощью IBLP.
Введя задачу в программу, получаем следующее оптимальное решение:
| 1 | -0,3 | 0,1 | -0,4 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 | Y9 | В |
| 1 | Y1 | 1 | 0 | 0,54 | -0,46 | 0 | -0,2 | 1,2 | 0 | 0 | 6,06 |
| -0,3 | Y2 | 0 | 1 | 0,4 | -0,6 | 0 | -2 | 2 | 0 | 0 | 2,6 |
| 0 | Y5 | 0 | 0 | -0,12 | -0,12 | 1 | -1,4 | 0,4 | 0 | 0 | 0,02 |
| 0 | Y8 | 0 | 0 | -0,2 | -0,2 | 0 | 0 | -1 | 1 | 0 | 0,2 |
| 0 | Y9 | 0 | 0 | -0,3 | -0,3 | 0 | 0 | -1 | 0 | 1 | 1,7 |
| T | 0 | 0 | 0,32 | 0,12 | 0 | 0,4 | 0,6 | 0 | 0 | 5,28 | |
.
Значение целевой
функции при
этом равно
5,28.
2. Решение по второй теореме двойственности.
Согласно
второй теореме
двойственности,
планы 
и
начальной
и двойственной
задачи соответственно
являются оптимальными
тогда и только
тогда, когда
выполняются
соотношения:
(5)
(6)
Покомпонентно для наших задач эти соотношения записываются следующим образом:
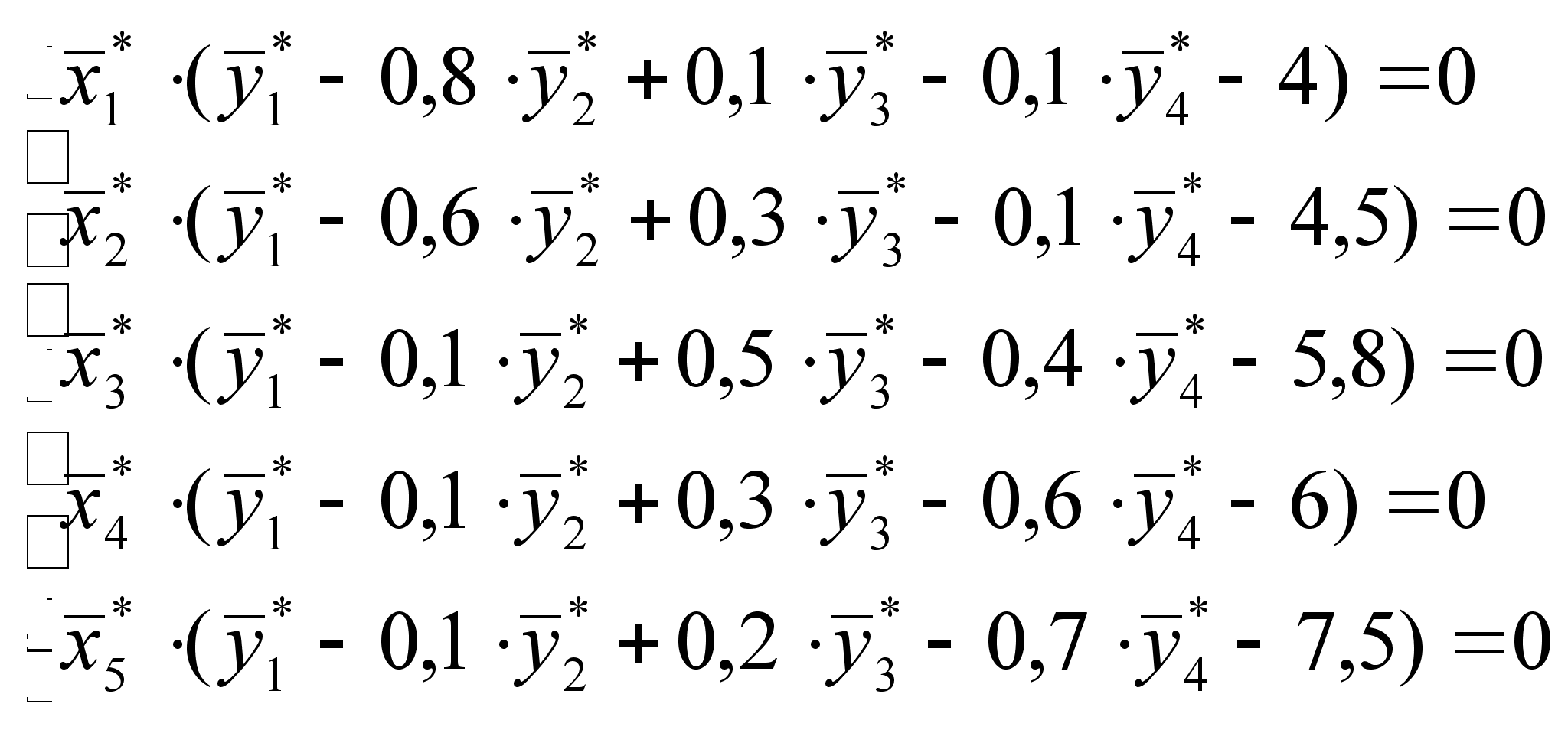(5).
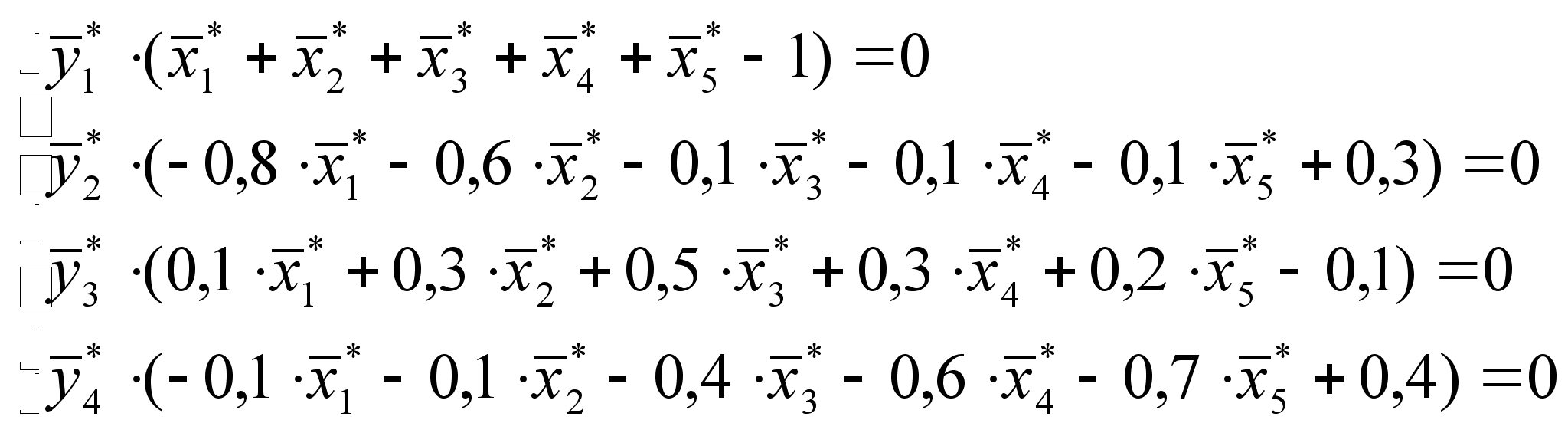(6)
Из системы
(5) видно, что во
втором и третьем
уравнениях
в скобках получается
ноль, поскольку
и 
положительны,
.
Из системы (6)
получаем, что
,
поскольку в
третьем и четвёртом
уравнениях
в скобках получаются
положительные
числа.
Из первого и третьего уравнений системы (5) имеем:
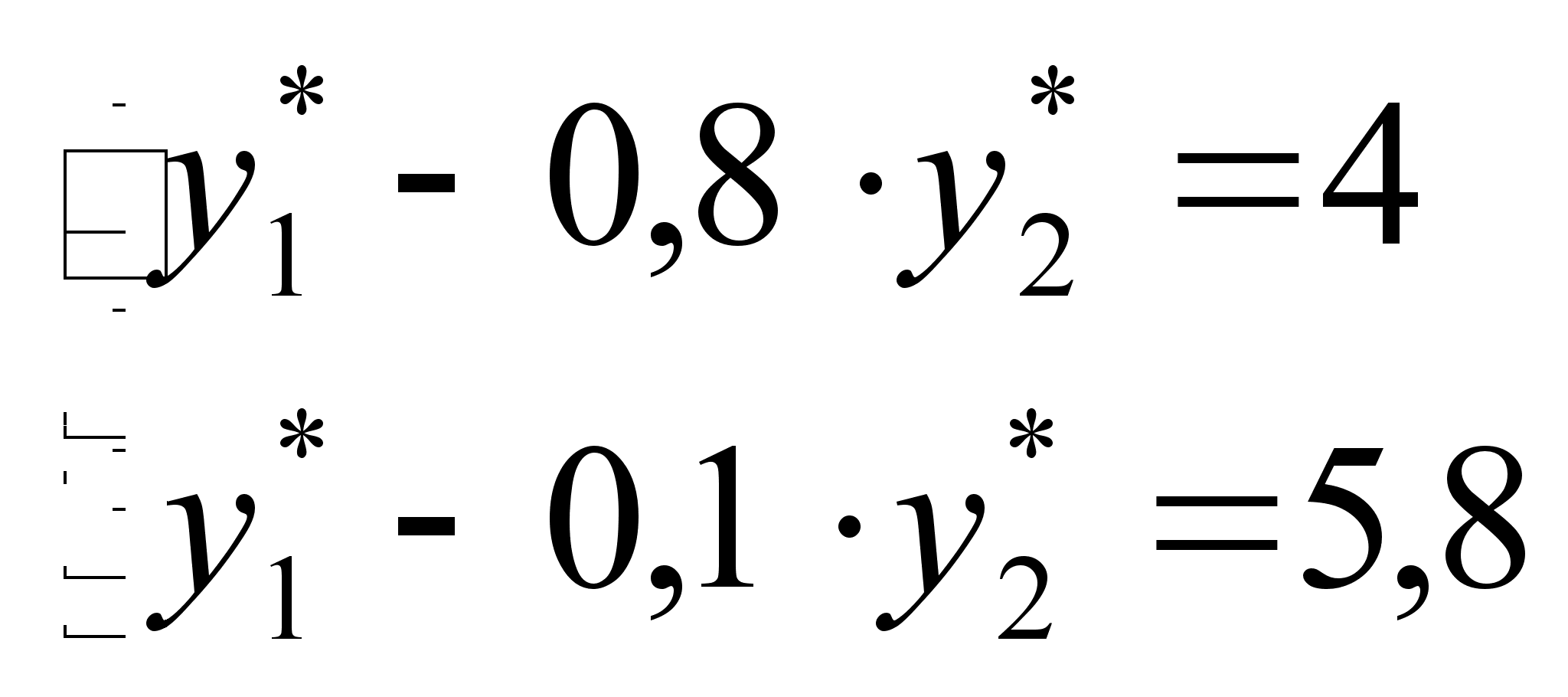
откуда 
Таким образом,
.
3. Решение с помощью симплекс-таблицы исходной задачи.
Запишем еще раз оптимальную симплекс-таблицу исходной задачи:
| 4 | 4,5 | 5,8 | 6 | 7,5 | 0 | 0 | 0 | M | M | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | -0,2 | 0 | 0,4 |
| 0 | X8 | 0,12 | 0 | 0 | 0,2 | 0,3 | 0,6 | 0 | 1 | -0,46 | 0 | 0,12 |
| 5,8 | X3 | -0,4 | 0 | 1 | 1 | 1 | -2 | 0 | 0 | 1,2 | 0 | 0,6 |
| 0 | X7 | 0,12 | 0 | 0 | 0,2 | 0,3 | -0,4 | 1 | 0 | 0,54 | -1 | 0,32 |
| F | -0,02 | 0 | 0 | -0,2 | -1,7 | -2,6 | 0 | 0 | -6,06 | 0 | 5,28 | |
| FM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | 0 | |
Из теории
известно, что
справедливы
следующие
формулы: 
(7);
(8).
В системе
ограничений
(2) исходной задачи
переменной
соответствует
первое ограничение,
содержащее
базисную переменную
,
переменной
– второе, содержащее
базисную переменную
,
переменной
– третье, содержащее
базисную переменную
и 
– четвёртое
с переменной
.
Запишем условие
(7) для оценок
,
,
и 
приведенной
симплекс-таблицы: 
; 
; 
; 
;
Теперь запишем условие (8) для нашего случая:
,
что покомпонентно
записывается
как: 
, 
, 
, 
,
откуда 
, 
, 
, 
С учетом того,
что мы решали
симплекс-методом
не исходную
задачу (1), а задачу
в канонической
форме (2), т.е. по
оптимальной
симплекс-таблице
мы можем найти
решение двойственной
задачи к канонической
форме исходной
задачи. Очевидно,
задача в симметричной
и канонической
форме – две
разные задачи,
отличающиеся
знаком и количеством
ограничений
в двойственных
задачах. Более
того, так как
все ограничения
в канонической
задаче – равенства,
то в двойственной
задаче все 
могут быть
любого знака,
поэтому наши
не являются
ошибкой. Но нам
необходимо
решить не
двойственную
к канонической
задаче, а двойственную
к симметричной.
Если сделать
замену 
,
то двойственная
задача к симметричной
задаче примет
форму двойственной
к канонической
задаче. Следовательно,
или .
Похожие работы
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...
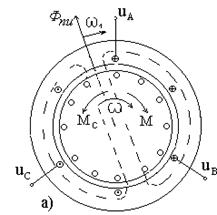
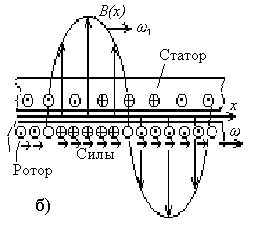
... концентрических окружностей с уменьшающимся радиусом по мере затухания колебаний скорости и момента. Аналогичная картина наблюдается при ступенчатом набросе нагрузки. 5. РАЗРАБОТКА ВИРТУАЛЬНОЙ ЛАБОРАТОРНОЙ РАБОТЫ НА БАЗЕ ВИРТУАЛЬНОЙ АСИНХРОННОЙ МАШИНЫ Иную возможность анализа АД представляет специализированный раздел по электротехнике Toolbox Power System Block. В его библиотеке имеются блоки ...
... Р- 122”.- Техническое описание. 3 “Техника чтения схем автоматического управления и технологического контроля”. – Энергоатомиздат, 1991.4 ДОКЛАД “Проект лабораторного стенда по изучению частотного электропривода на базе автономного инвертора напряжения фирмы OMRON”. В настоящее время на АО “Северсталь” происходит активное внедрение частотных преобразователей. Это объясняется тем, что частотное ...
0 комментариев