Навигация
Рассмотрим случай со свободной переменной
2. Рассмотрим случай со свободной переменной.
а) ![]() ,
тогда
,
тогда ![]()
Условие
оптимальности
оценки: ![]() =>
=> ![]() =>
=> ![]() .
.
В данном
случае ![]() ,
,
![]() .
.
Таким образом,
решение будет
оставаться
оптимальным,
при уменьшении
коэффициента
при ![]() до 3,98 у.е. за
единицу и
неограниченном
увеличении.
Значение целевой
функции при
этом не изменится.
до 3,98 у.е. за
единицу и
неограниченном
увеличении.
Значение целевой
функции при
этом не изменится.
б) Будем руководствоваться аналогичными рассуждениями при вычислении интервалов устойчивости для четвёртого и пятого ресурсов.
![]() ,
,
![]() или
или ![]() ,
,![]() .
.
![]() ,
,
![]() или
или ![]() ,
,![]()
Оптимальные решения при конкретных изменениях коэффициентов.
а)стоимость второго сырья увеличилась до 4,5 у.е
Интервал
устойчивости
коэффициента
целевой функции ![]() .
Цена 4,5 у.е. входит в этот
интервал, значит
оптимальное
решение не
изменится, а
критерий станет
.
Цена 4,5 у.е. входит в этот
интервал, значит
оптимальное
решение не
изменится, а
критерий станет ![]() у.е.
у.е.
б) стоимость третьего сырья уменьшилась до 3 у.е
Интервал
устойчивости
для ![]() .
3 у.е. (
.
3 у.е. (![]() )
не принадлежит
интервалу,
значит какие-то
оценки будут
не оптимальными:
)
не принадлежит
интервалу,
значит какие-то
оценки будут
не оптимальными:
– при ![]() :
:
![]() ;
;
– при ![]() :
:
![]() ;
;
– при ![]() :
:
![]() ;
;
– при ![]() :
:
![]() ;
;
– при ![]() :
:
![]() ;
;
![]() .
.
Скорректируем симплекс-таблицу:
| 4 | 4,5 | 3 | 6 | 7,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | -0,2 | 0 | 0,4 |
| 0 | X8 | 0,12 | 0 | 0 | 0,2 | 0,3 | 0,6 | 0 | 1 | -0,46 | 0 | 0,12 |
| 3 | X3 | -0,4 | 0 | 1 | 1 | 1 | -2 | 0 | 0 | 1,2 | 0 | 0,6 |
| 0 | X7 | 0,12 | 0 | 0 | 0,2 | 0,3 | -0,4 | 1 | 0 | 0,54 | -1 | 0,32 |
| F | 1,1 | 0 | 0 | -3 | -4,5 | 3 | 0 | 0 | -9,42 | 0 | 3,6 | |
Через две итерации получаем оптимальную симплекс-таблицу:
| 4 | 4,5 | 3 | 6 | 7,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4 | X1 | 1 | 1 | 0 | -0,666 | -1 | 0 | 0 | -3,33 | 1,333 | 0 | 0 |
| 0 | X6 | 0 | -0,2 | 0 | 0,466 | 0,7 | 1 | 0 | 2,333 | -1,03 | 0 | 0,2 |
| 3 | X3 | 0 | 0 | 1 | 1,666 | 2 | 0 | 0 | 3,333 | -0,333 | 0 | 0,1 |
| 0 | X7 | 0 | -0,2 | 0 | 0,466 | 0,7 | 0 | 1 | 1,333 | -0,033 | -1 | 0,4 |
| F | 0 | -0,5 | 0 | -3,66 | -5,5 | 0 | 0 | -3,33 | 4,333 | 0 | 3 | |
Получим
оптимальное
решение ![]() .
Стоимость
сплава понизилась
до 3 у.е. за единицу.
.
Стоимость
сплава понизилась
до 3 у.е. за единицу.
в) издержки на первое сырьё возросли до 6 у.е
Стоимость
первого сырья
может изменяться
в пределах ![]() .
6 у.е. входят в
интервал, значит
оптимальное
решение не
изменится, а
также останется
прежнем критерий
(
.
6 у.е. входят в
интервал, значит
оптимальное
решение не
изменится, а
также останется
прежнем критерий
(![]() ,
,![]() ).
).
г) издержки на четвёртый ресурс упали до 4 у.е.
При падении
издержек до
4 у.е. за тонну
оптимальное
решение должно
измениться,
т.к. нижняя граница
интервала
устойчивости
– 5,8 у.е. Оценка
![]() .
.
| 4 | 4,5 | 5,8 | 4 | 7,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | -0,2 | 0 | 0,4 |
| 0 | X8 | 0,12 | 0 | 0 | 0,2 | 0,3 | 0,6 | 0 | 1 | -0,46 | 0 | 0,12 |
| 5,8 | X3 | -0,4 | 0 | 1 | 1 | 1 | -2 | 0 | 0 | 1,2 | 0 | 0,6 |
| 0 | X7 | 0,12 | 0 | 0 | 0,2 | 0,3 | -0,4 | 1 | 0 | 0,54 | -1 | 0,32 |
| F | -0,02 | 0 | 0 | 1,8 | -1,7 | -2,6 | 0 | 0 | -6,06 | 0 | 5,28 | |
Оптимальная симплекс-таблица:
| 4 | 4,5 | 5,8 | 4 | 7,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | -0,2 | 0 | 0,4 |
| 4 | X4 | 0,6 | 0 | 0 | 1 | 1,5 | 3 | 0 | 5 | -2,3 | 0 | 0,6 |
| 5,8 | X3 | -1 | 0 | 1 | 0 | -0,5 | -5 | 0 | -5 | 3,5 | 0 | 0 |
| 0 | X7 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | -1 | 1 | -1 | 0,2 |
| F | -1,1 | 0 | 0 | 0 | -4,4 | -8 | 0 | -9 | 10,2 | 0 | 4,2 | |
С помощью
симплекс-метода
получаем оптимальное
решение ![]() и оптимальное
значение критерия
и оптимальное
значение критерия
![]() у.е.
у.е.
В этом пункте, как и в предыдущем, можно рассматривать два случая: изменение значений коэффициентов, соответствующих базисным переменным и свободным переменным. Изменение значений коэффициентов при базисных переменных приводит к изменению базисной матрицы, поэтому проанализировать это довольно сложно, ленче решить задачу заново. Следовательно. Рассмотрим случай с изменением коэффициента при свободной переменной.
Возьмем,
например, как
изменяющийся
коэффициент
![]() .
Его изменение
влечёт за собой
изменение
оценки только
свободной
переменной
.
Его изменение
влечёт за собой
изменение
оценки только
свободной
переменной
![]() :
:
![]() .
Для того, чтобы
решение оставалось
оптимальным,
необходима
неположительность
оценки:
.
Для того, чтобы
решение оставалось
оптимальным,
необходима
неположительность
оценки: ![]() т.е.
т.е. ![]() .
Интервал устойчивости
коэффициента
.
Интервал устойчивости
коэффициента
![]() .
.
Возьмём также для наглядности изменение ещё одного коэффициента, т.к. полученный выше результат означает, что содержание сплава (т.е всех компонентов) в первом сырье может меняться от 0% до 100% (формально от 0% до 100,3%).
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
т.е. содержание
свинца в первом
сырье варьируется
в пределах от
0% до 100% (
,
т.е. содержание
свинца в первом
сырье варьируется
в пределах от
0% до 100% (![]() и
и ![]() экономического
смысла не имеют).
экономического
смысла не имеют).
В качестве примера только из чистого математического любопытства приведем такую фантастическую ситуацию: содержание сплава в первом сырье возросло до:
а) 100,2%
![]() ,
,![]() (входит в интервал
устойчивости).
Оптимальный
план выпуска
не изменится
(входит в интервал
устойчивости).
Оптимальный
план выпуска
не изменится
![]() и оптимальное
значение целевой
функции останется
и оптимальное
значение целевой
функции останется
![]() .
.
б) 110%
![]() ,
,
![]() (не входит в
интервал
устойчивости).
(не входит в
интервал
устойчивости).
![]() –
оценка не
оптимальная.
–
оценка не
оптимальная.
Симплекс-методом получим оптимальное решение:
![]() ,
,
![]() .
.
Предположим, что появилась возможность использовать новый вид сырья, в котором содержится 40% олова, 60% цинка и 30% свинца, и который обладает стоимостью 3,5 у.е. за единицу. Определим новый план производства.
Пусть ![]() –
доля шестого
(нового) сырья
в сплаве. Тогда:
–
доля шестого
(нового) сырья
в сплаве. Тогда:
![]()
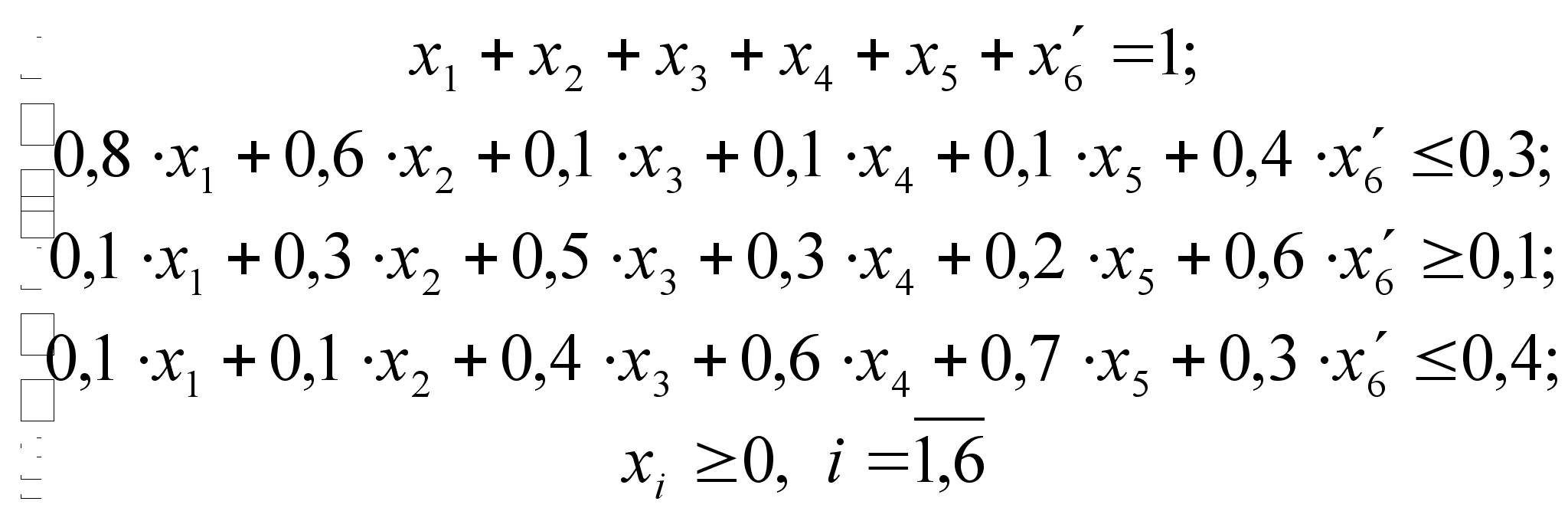
Решим, выгодно
ли использовать
новое сырьё.
Для этого
воспользуемся
двойственными
оценками ![]() .
.
Доход на тонну
нового сырья
будет равен
![]() ,
а затраты – 3,5
у.е. (Новое ограничение
в двойственной
задаче
,
а затраты – 3,5
у.е. (Новое ограничение
в двойственной
задаче ![]() )
Тонна сырья
приносит больше
дохода, чем
издержек на
1 у.е., поэтому
будем увеличивать
использование
этого сырья.
)
Тонна сырья
приносит больше
дохода, чем
издержек на
1 у.е., поэтому
будем увеличивать
использование
этого сырья.
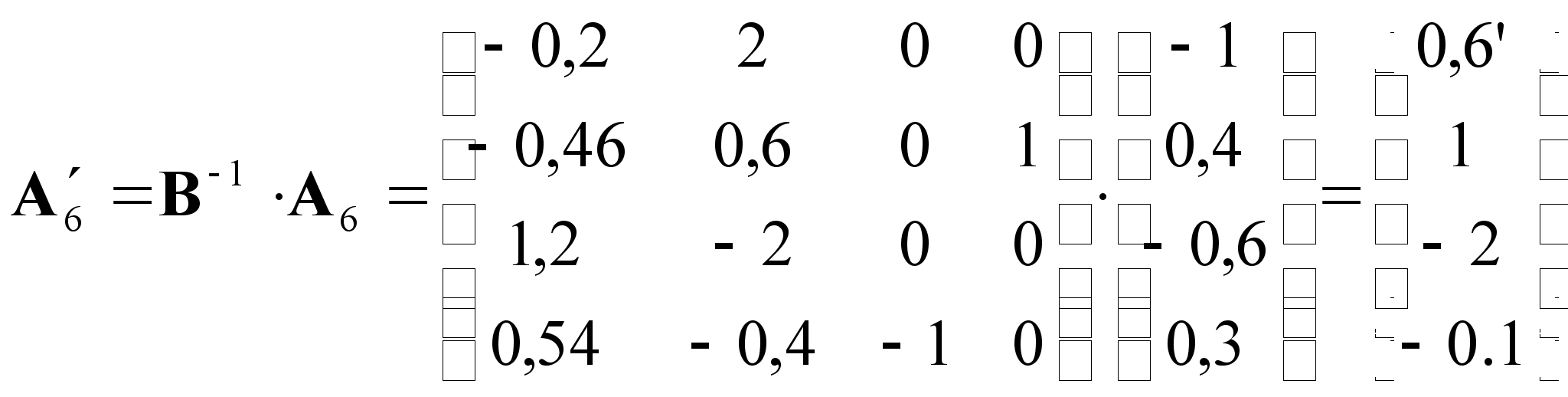
![]()
Запишем новую симплекс-таблицу с учётом новой переменной:
| 4 | 4,5 | 5,8 | 6 | 7,5 | 3,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6’ | X6 | X7 | X8 | X9 | X10 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 0,6’ | 2 | 0 | 0 | -0,2 | 0 | 0,4 |
| 0 | X8 | 0,12 | 0 | 0 | 0,2 | 0,3 | 1 | 0,6 | 0 | 1 | -0,46 | 0 | 0,12 |
| 5,8 | X3 | -0,4 | 0 | 1 | 1 | 1 | -2 | -2 | 0 | 0 | 1,2 | 0 | 0,6 |
| 0 | X7 | 0,12 | 0 | 0 | 0,2 | 0,3 | -0,1 | -0,4 | 1 | 0 | 0,54 | -1 | 0,32 |
| F | -0,02 | 0 | 0 | -0,2 | -1,7 | 1 | -2,6 | 0 | 0 | -6,06 | 0 | 5,28 | |
Оптимальная симплекс-таблица:
| 4 | 4,5 | 5,8 | 6 | 7,5 | 3,5 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6’ | X6 | X7 | X8 | X9 | X10 | В |
| 3,5 | X6’ | 2,333 | 1,666 | 0 | 0 | 0 | 1 | 3,333 | 0 | 0 | -0,333 | 0 | 0,666 |
| 0 | X8 | -0,066 | -0,133 | 0 | 0,2 | 0,3 | 0 | 0,333 | 0 | 1 | -0,433 | 0 | 0,066 |
| 5,8 | X3 | -1,33 | -0,666 | 1 | 1 | 1 | 0 | -3,33 | 0 | 0 | 1,333 | 0 | 0,333 |
| 0 | X7 | 0,633 | 0,366 | 0 | 0,2 | 0,3 | 0 | 0,333 | 1 | 0 | 0,466 | -1 | 0,466 |
| F | -3,56 | -2,53 | 0 | -0,2 | -1,7 | 0 | -7,66 | 0 | 0 | -6,566 | 0 | 4,266 | |
Оптимальное
решение будет
![]() ,
,
![]() .
Это означает,
что для производства
нового сплава
будет использоваться
33,3% третьего сырья
и 66,6% нового шестого
сырья. Минимальная
стоимость
сплава будет
4,266 у.е. Видим, что
использование
нового вида
сырья действительно
выгодно, т.к.
издержки на
производство
сплава снизились
с 5,28 у.е. за единицу
до 4,266 у.е.
.
Это означает,
что для производства
нового сплава
будет использоваться
33,3% третьего сырья
и 66,6% нового шестого
сырья. Минимальная
стоимость
сплава будет
4,266 у.е. Видим, что
использование
нового вида
сырья действительно
выгодно, т.к.
издержки на
производство
сплава снизились
с 5,28 у.е. за единицу
до 4,266 у.е.
Пусть для производства сплава нужно использовать ещё один компонент – медь, содержащуюся в сырье в количествах 40%, 10%, 20%, 20% и 30% соответственно. Содержание её в новом сплаве не должно быть меньше 20%.
Система ограничений будет иметь вид:
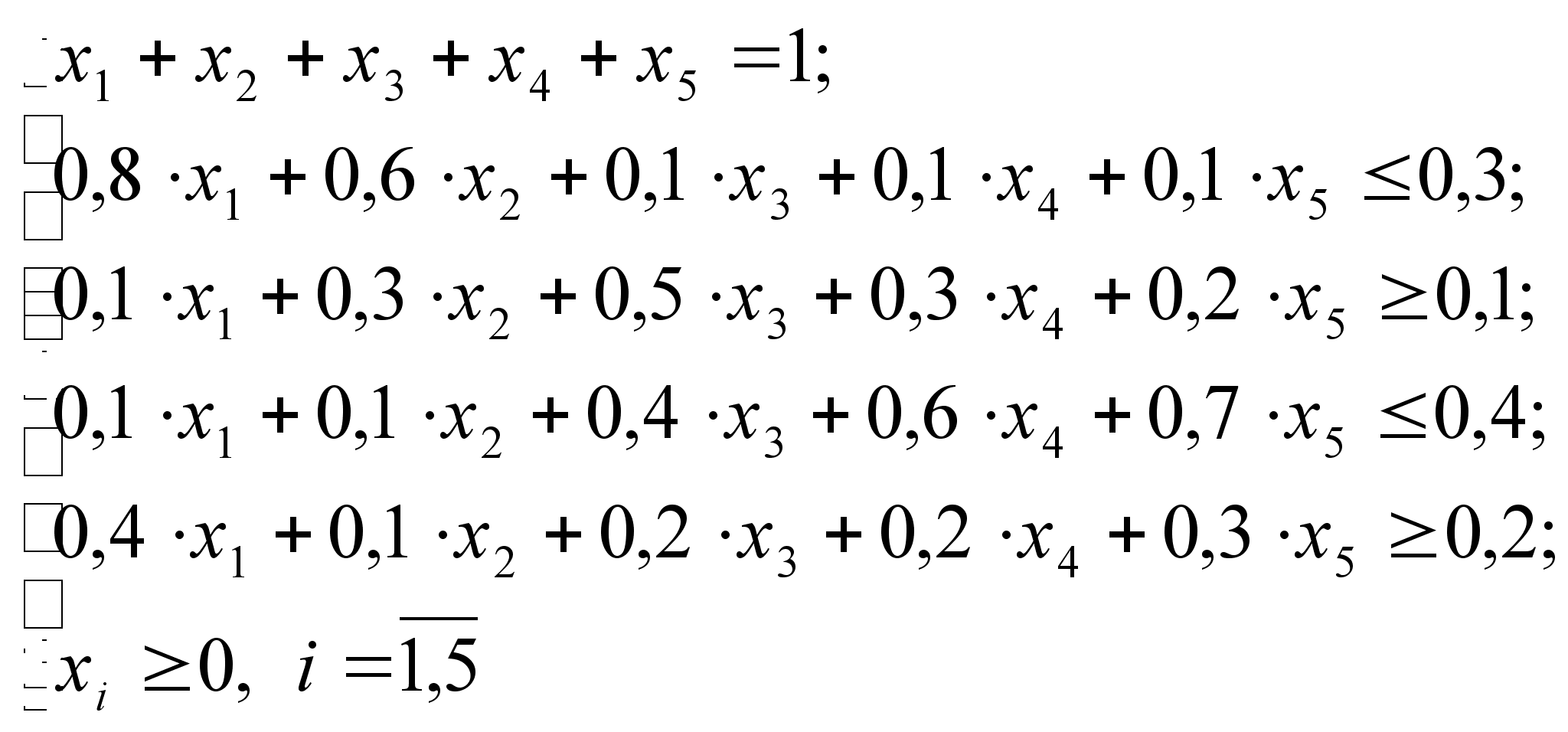
Оптимальное
решение первоначальной
задачи: ![]() .
Проверим,
удовлетворяет
ли оно новому
ограничению:
.
Проверим,
удовлетворяет
ли оно новому
ограничению:
![]() .
.
Ограничение не выполняется, поэтому для решения задачи приведём новое ограничение к канонической форме:
![]()
Исключив из него все базисные переменные, добавим его в оптимальную симплекс-таблицу.
![]()
![]()
![]()
После несложных
вычислений
получим:
![]() .
.
Новая симплекс таблица будет выглядеть следующим образом:
| 4 | 4,5 | 5,8 | 6 | 7,5 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | В |
| 4,5 | X2 | 1,4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | -0,2 | 0 | 0 | 0,4 |
| 0 | X8 | 0,12 | 0 | 0 | 0,2 | 0,3 | 0,6 | 0 | 1 | -0,46 | 0 | 0 | 0,12 |
| 5,8 | X3 | -0,4 | 0 | 1 | 1 | 1 | -2 | 0 | 0 | 1,2 | 0 | 0 | 0,6 |
| 0 | X7 | 0,12 | 0 | 0 | 0,2 | 0,3 | -0,4 | 1 | 0 | 0,54 | -1 | 0 | 0,32 |
| 0 | X11 | 0,34 | 0 | 0 | 0 | 0,1 | 0,2 | 0 | 0 | -0,22 | 0 | 1 | 0,04 |
| F | -0,02 | 0 | 0 | -0,2 | -1,7 | -2,6 | 0 | 0 | -6,06 | 0 | 0 | 5,28 | |
Оптимальное решение получим с помощью двойственного симплекс-метода.
| 4 | 4,5 | 5,8 | 6 | 7,5 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| Св | Б.П. | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | В |
| 4,5 | X2 | 0 | 1 | 0 | 0 | -0,411 | 1,176 | 0 | 0 | 4,117 | 0,705 | 0 | 0,235 |
| 0 | X8 | 0 | 0 | 0 | 0,2 | 0,264 | 0,529 | 0 | 1 | 0,353 | -0,382 | 0 | 0,106 |
| 5,8 | X3 | 0 | 0 | 1 | 1 | 1,117 | -1,76 | 0 | 0 | -1,17 | 0,941 | 0 | 0,647 |
| 0 | X7 | 0 | 0 | 0 | 0,2 | 0,264 | -0,47 | 1 | 0 | 0,353 | 0,617 | -1 | 0,305 |
| 4 | X1 | 1 | 0 | 0 | 0 | 0,294 | 0,588 | 0 | 0 | -2,94 | -0,647 | 0 | 0,117 |
| F | 0 | 0 | 0 | -0,2 | -1,69 | -2,58 | 0 | 0 | -0,058 | -6,047 | 0 | 5,282 | |
Оптимальное
решение: ![]() .
Это значит, что
для производства
сплава с учётом
примеси меди
необходимо
взять 11,7% первого сырья,
23,5% второго сырья
и 64,7% третьего
сырья. Минимальная
стоимость
единицы такого
сплава будет
5,282 у.е.
.
Это значит, что
для производства
сплава с учётом
примеси меди
необходимо
взять 11,7% первого сырья,
23,5% второго сырья
и 64,7% третьего
сырья. Минимальная
стоимость
единицы такого
сплава будет
5,282 у.е.
13
Лабораторная работа № 5
Телешовой Елизаветы, гр. 726,
Транспортные задачи линейного программирования. 1. Постановка задачи.В некотором царстве, некотором государстве жил-был кот Василий, который очень любил мышей… на обед. А обедал он исключительно в амбаре своего хозяина, да так хорошо, что бедные мыши и носу не могли высунуть из своих нор. Но всю жизнь в норе не просидишь, есть то хочется, и стали мыши думать и гадать, как им провести кота Василия и до заветных пищевых ресурсов амбара добраться.
В амбаре было 4 мышиных норы: в первой проживало 15 мышей, во второй – 20, в третьей – 10 мышей, а в четвертой – 25 мышей, а также 5 источников пищи, от которых и кормилась вся эта орава мышей: у окорока – 5 мышей, у мешка крупы – 18 мышей, у мешка муки – 17 мышей, у мешка картошки – 22 мыши и у стопки старых газет и журналов эротического содержания – 8 мышей.
И тут мыши вспомнили, что когда-то в стопке журналов лежала книжка по математическому программированию. Конечно мыши давным-давно успели ее сгрызть, но кое-что из нее они, пока грызли, прочитать успели, в частности, как решать транспортные задачи.
Считая что
![]() –
количество
мышей из
–
количество
мышей из ![]() -той
норы, питающихся
у
-той
норы, питающихся
у ![]() -того
источника пищи,
-того
источника пищи, ![]() –
количество
мышей, проживающих
в
–
количество
мышей, проживающих
в ![]() -той
норе,
-той
норе, ![]() –
количество
мышей, питающихся
у
–
количество
мышей, питающихся
у ![]() -того
источника пищи,
мыши определили,
что для того,
чтобы были все
они были сыты,
необходимо
выполнение
2 условий:
-того
источника пищи,
мыши определили,
что для того,
чтобы были все
они были сыты,
необходимо
выполнение
2 условий:
1)![]() ;
;
2)![]() ;
;
ну и конечно
![]()
Исходя из этих условий они составили математическую модель процесса своего питания:
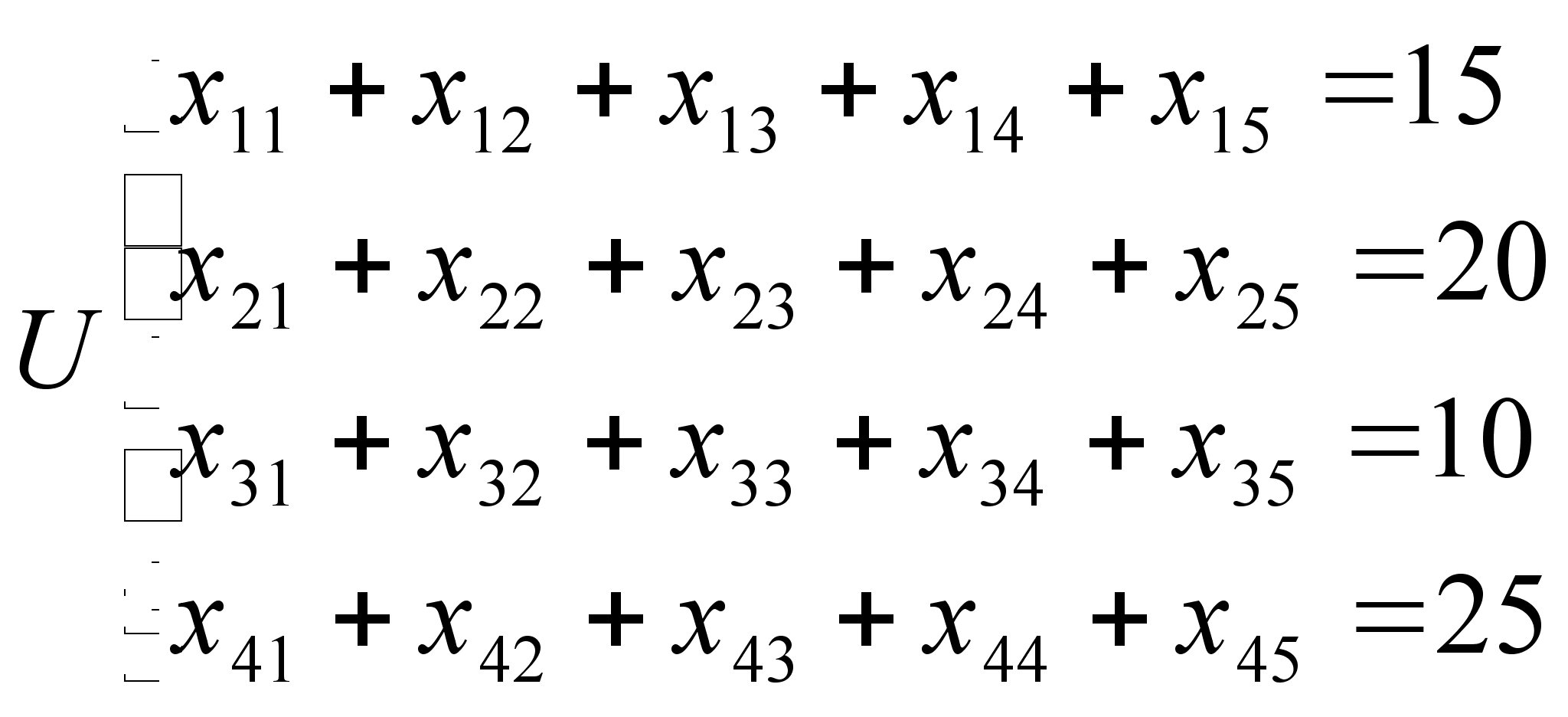 ;
; 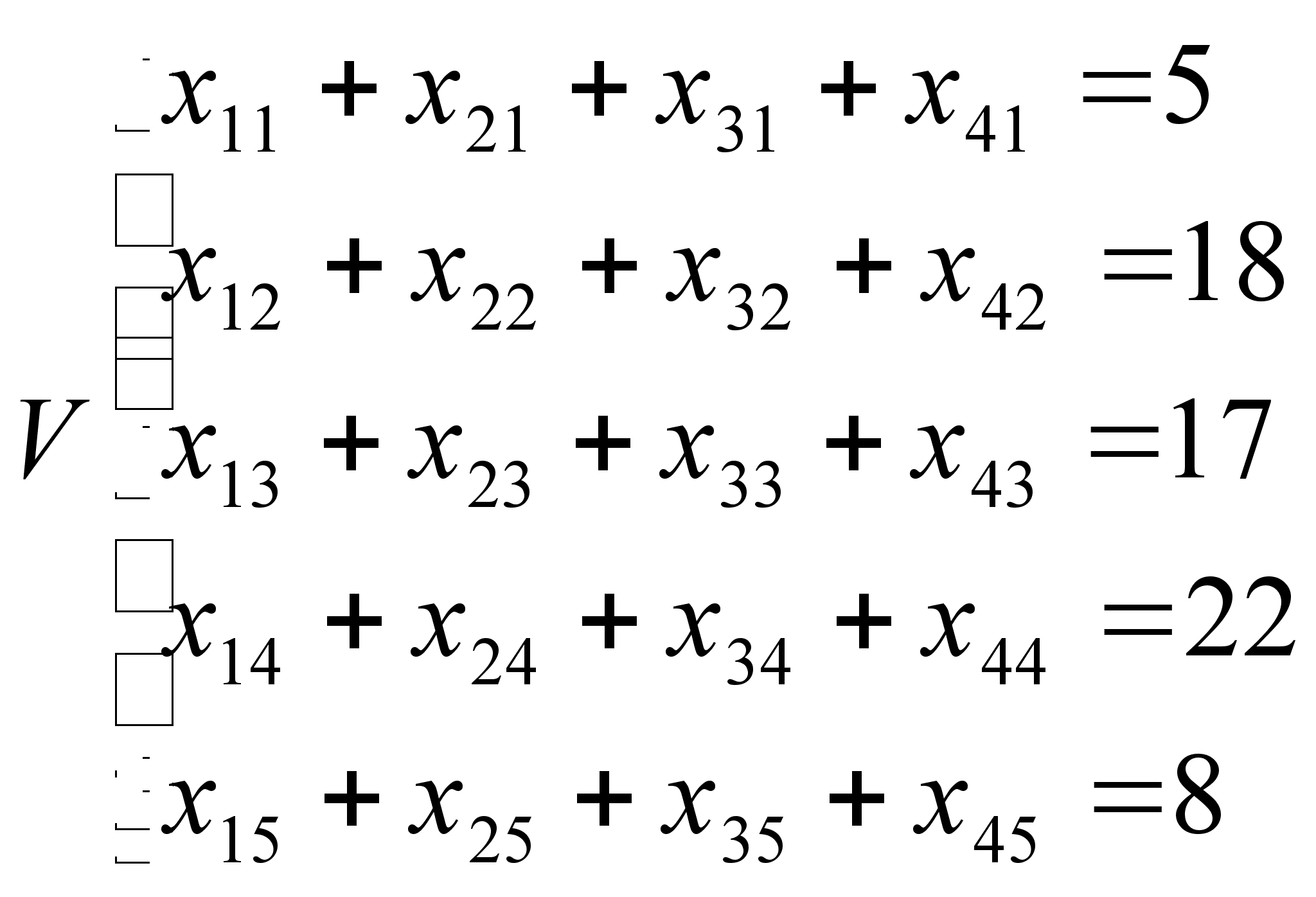 ;
; ![]()
Ну, и для наглядности нарисовали ее в виде таблицы:
| | окорок | мешок крупы | мешок муки | мешок картошки | журналы | |
| 5 | 18 | 17 | 22 | 8 | ||
| нора 1 | 15 |
|
|
|
|
|
| нора 2 | 20 |
|
|
|
|
|
| нора 3 | 10 |
|
|
|
|
|
| нора 4 | 25 |
|
|
|
|
|
В левом верхнем
углу каждой
ячейки таблицы
мыши указали
число попавших
в лапы кота (в
процентах) по
отношению к
общему числу
мышей из ![]() -той
норы, питающихся
у
-той
норы, питающихся
у ![]() -того
источника пищи.
Эти данные они
также записали
в виде матрицы
(в относительных
единицах):
-того
источника пищи.
Эти данные они
также записали
в виде матрицы
(в относительных
единицах):
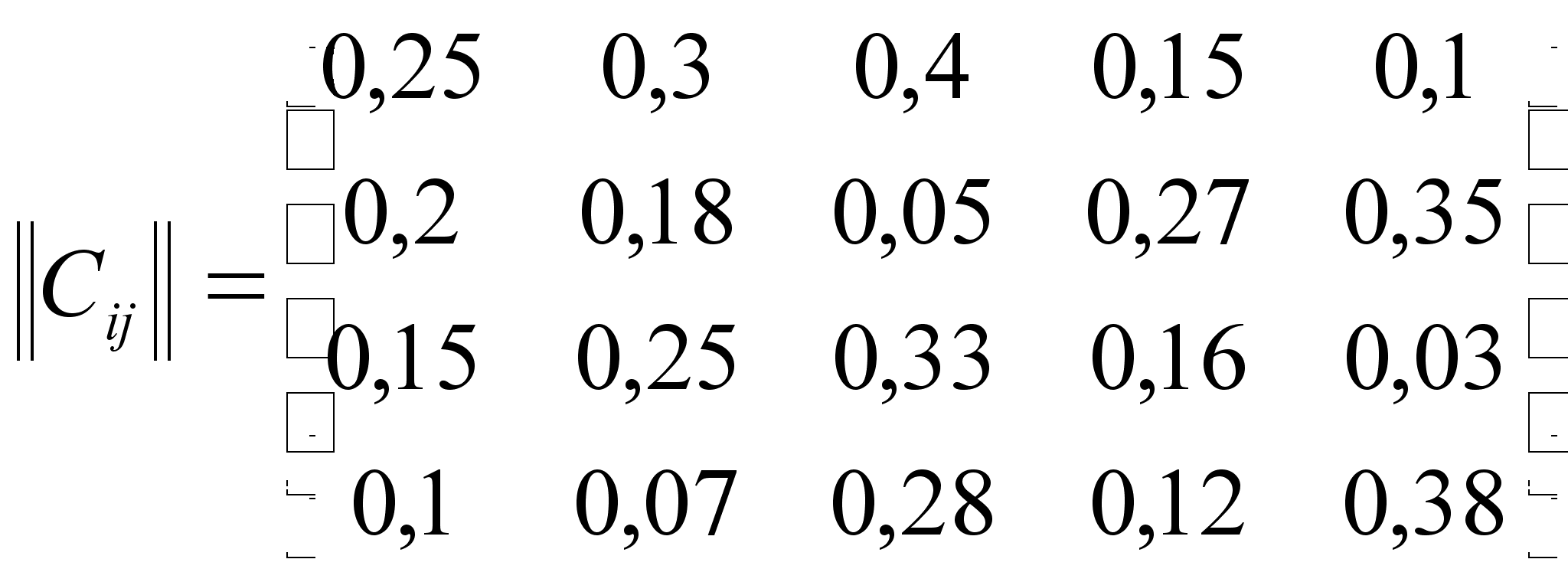 .
.
Безусловно, цель мышей – добраться до еды с минимальными потерями по дороге, то есть:
![]() .
.
Таким образом:
![]()
Необходимо,
конечно, оценить
и выгодность
передвижения
из каждой норы
к каждому пищевому
ресурсу. Для
этого мыши
оценили так
называемые
потенциалы
нор (![]() )
и источников
пищи (
)
и источников
пищи (![]() ).
Так как их цель
– минимизировать
потери, то сумма
потенциалов
в каждом случае
не должна превышать
затрат, т.е.
необходимо
выполнение
следующих
условий:
).
Так как их цель
– минимизировать
потери, то сумма
потенциалов
в каждом случае
не должна превышать
затрат, т.е.
необходимо
выполнение
следующих
условий:
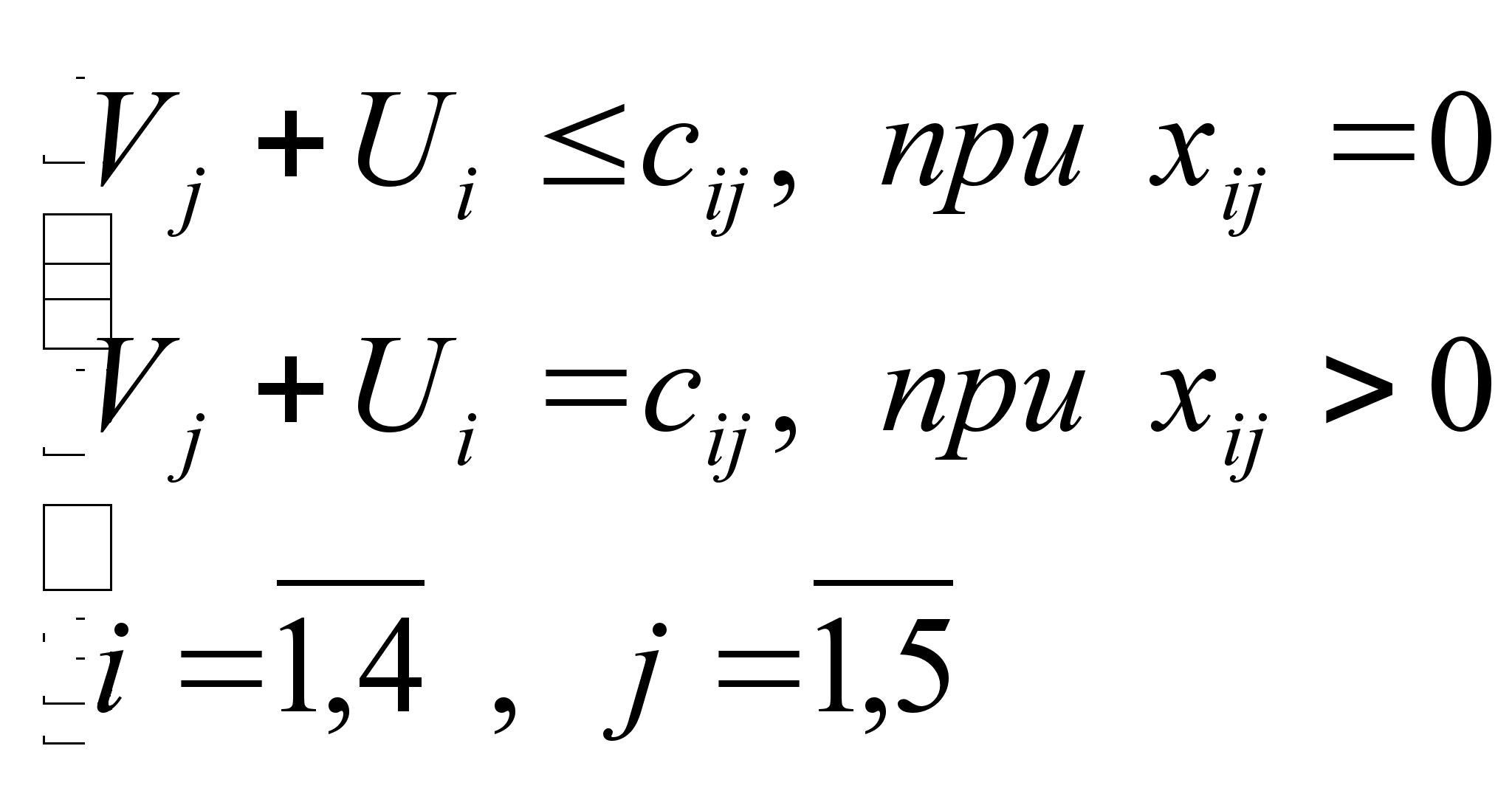 (1).
(1).
Система (1) и будет служить в дальнейшем критерием оптимальности плана.
Запишем подробно двойственную задачу на основе этого ограничения:
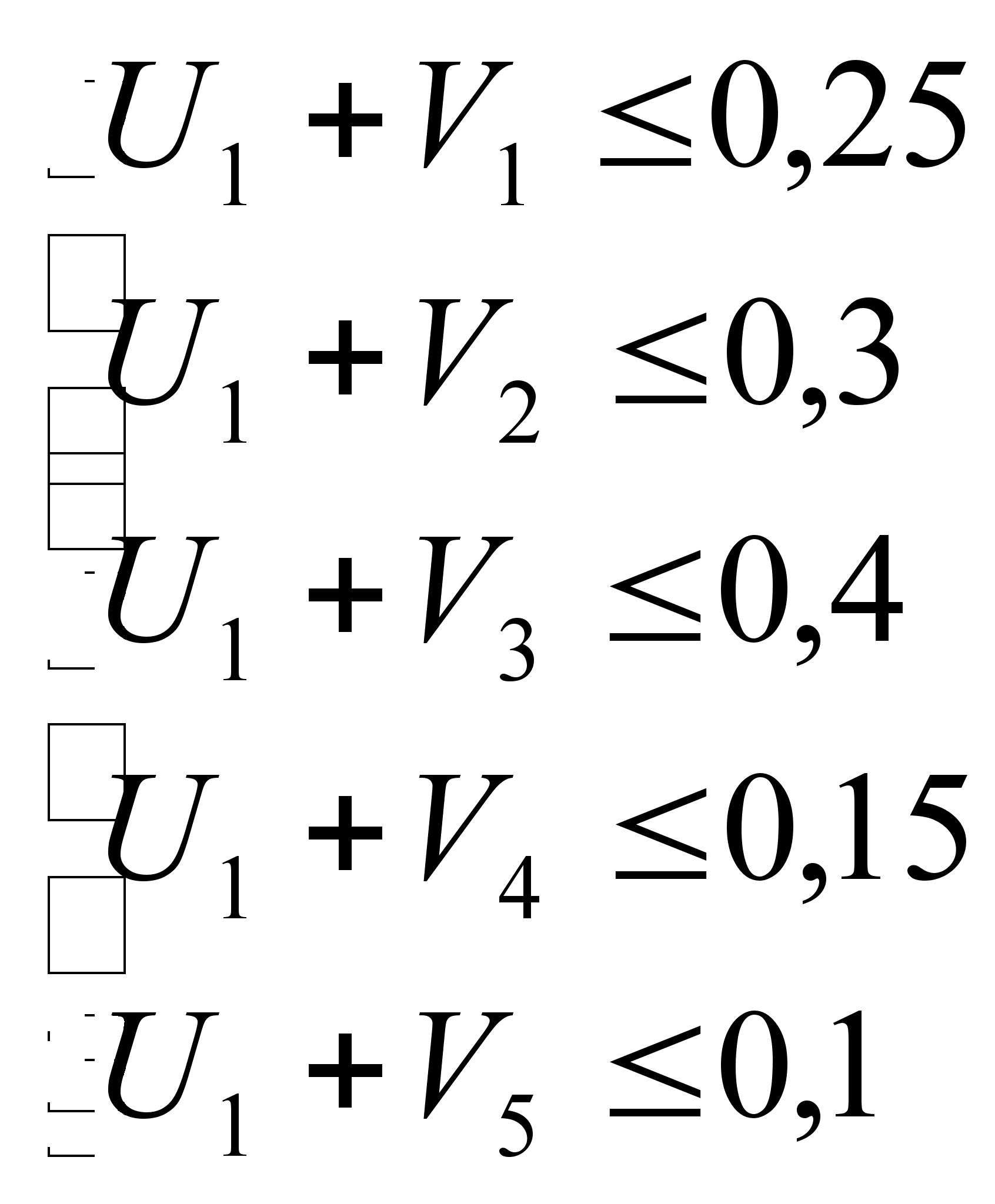 ;
;
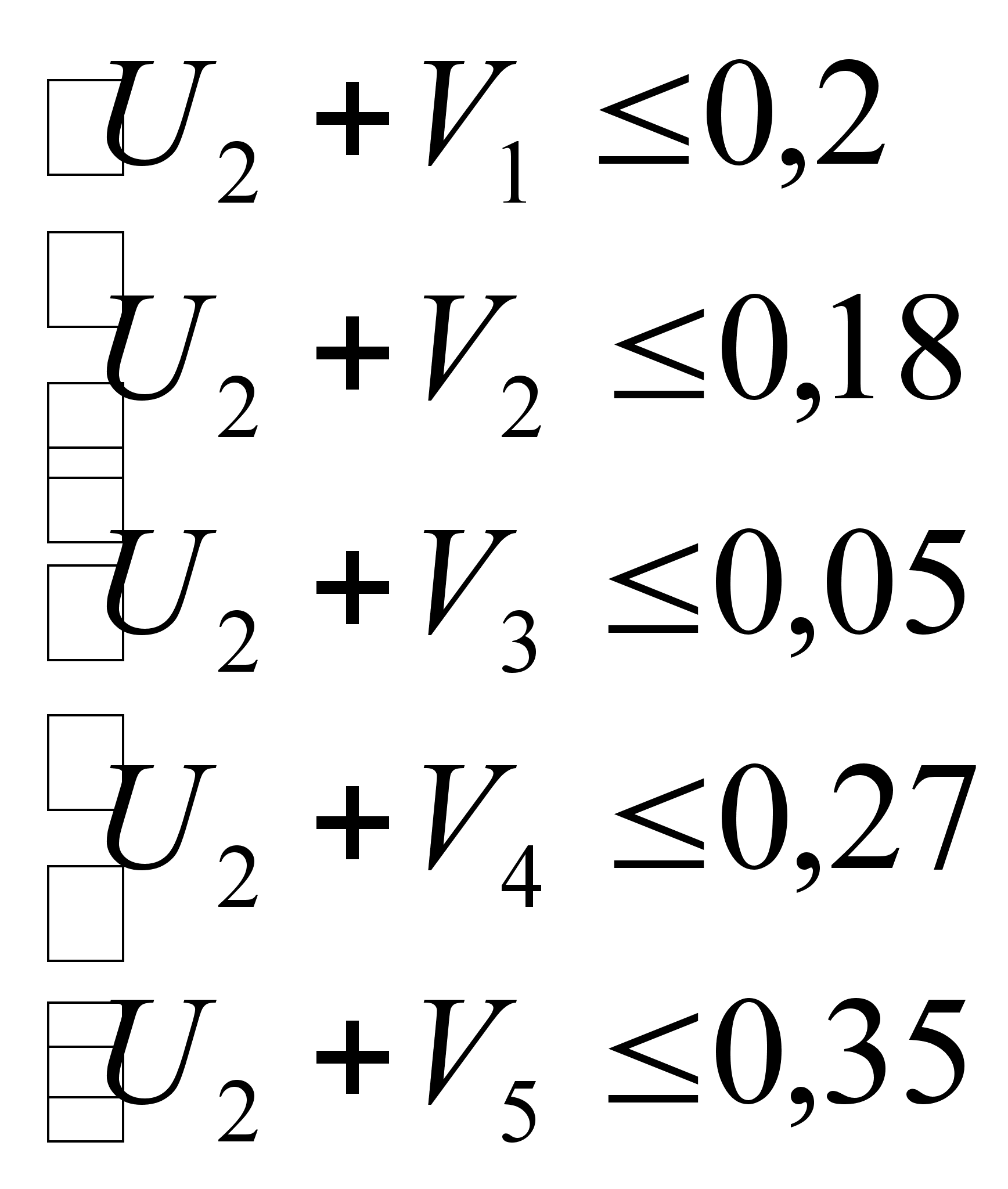 ;
;
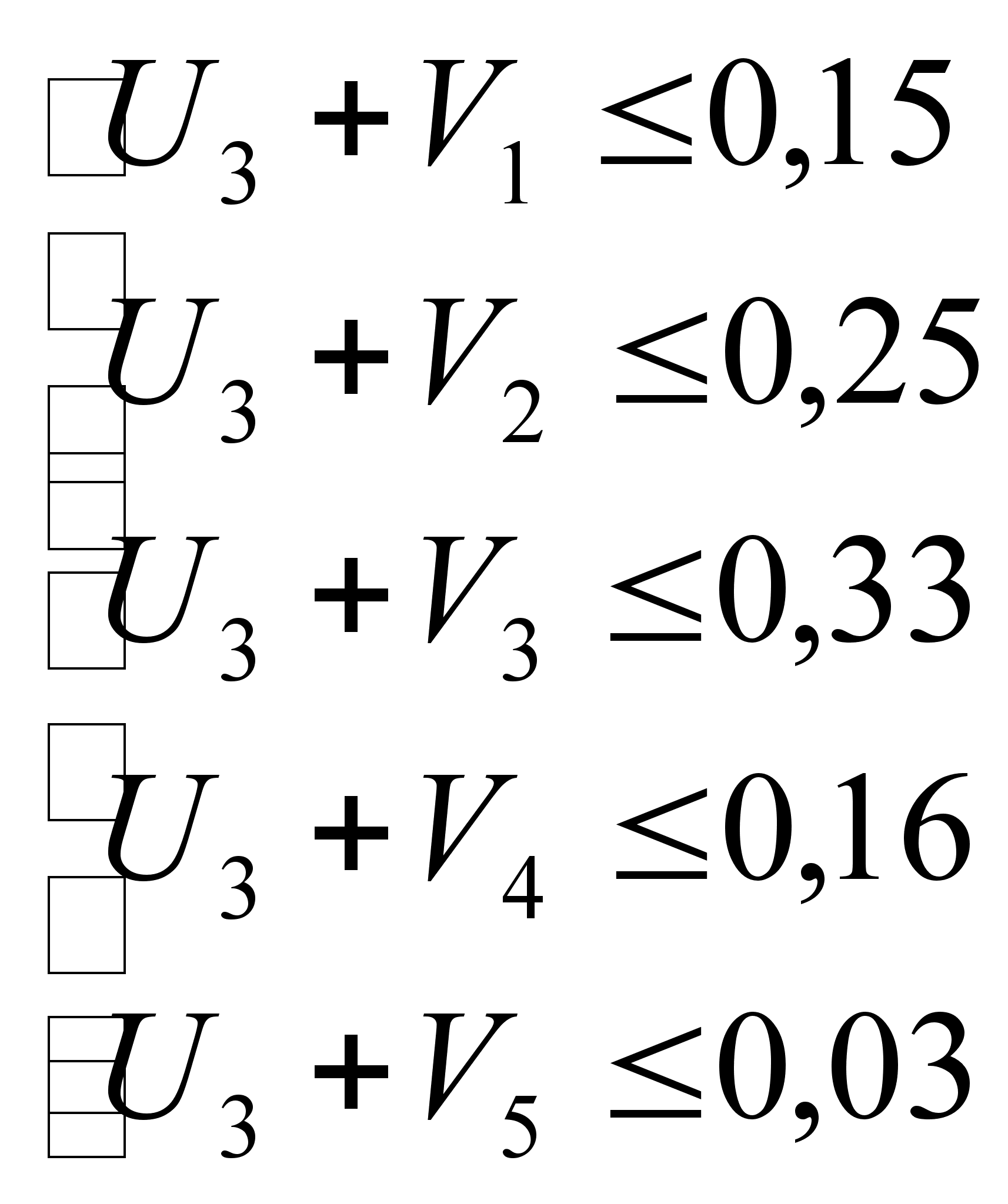 ;
;
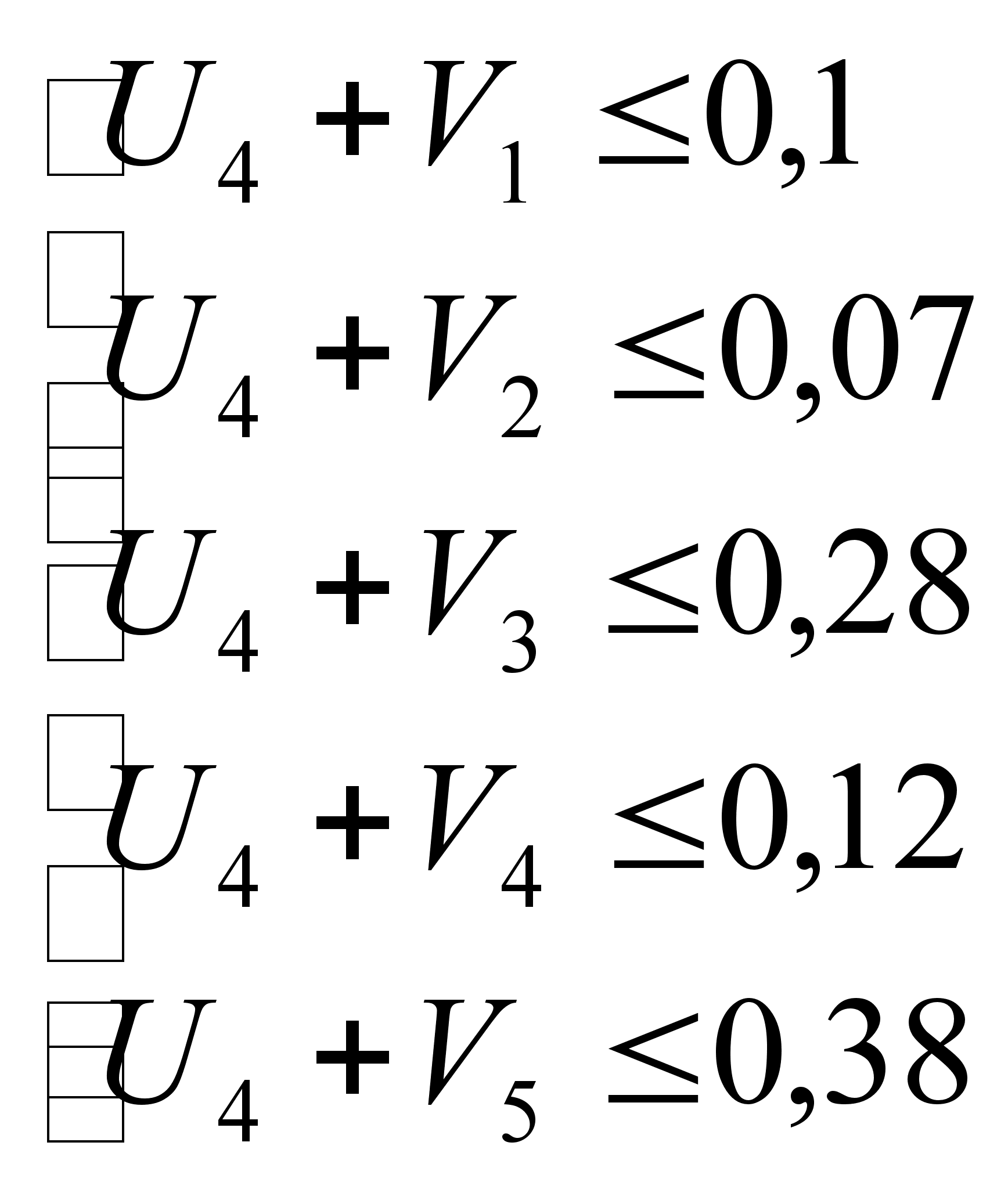 ;
;
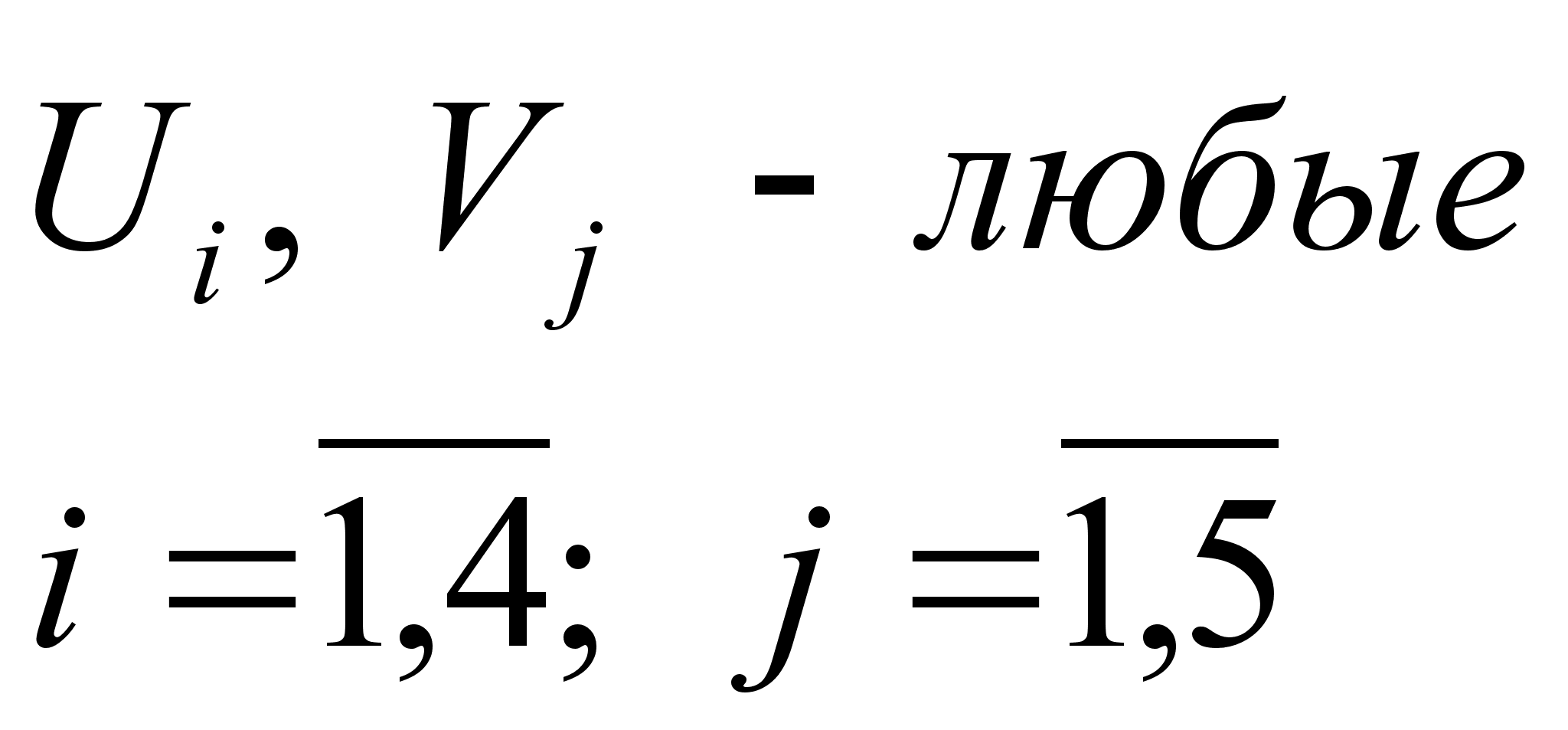
Критерием двойственной задачи будет максимизация выгодности:
![]()
Первое, что пришло на ум мышам – использовать те источники пищи, доступ к которым легче, и они решили построить начальный опорный план по методу максимальной загрузки, исходя из формулы:
![]() (2).
(2).
т.е. выбираются те варианты, которые могут обеспечить едой максимальное количество мышей, и эти варианты будут использоваться в соответствии с (2).
Поскольку хотят есть все мыши во всех норах, то модель закрытая, т.е.
![]() .
.
Общая схема построения начального опорного плана по методу максимальной загрузки такова:
1) Выбираем коммуникацию, которую можно больше всего загрузить.
2) Максимально ее загружаем в соответствии с (2).
3) Корректируем объемы производства и потребления на величину выбранной перевозки, вычисляя остатки производства и потребления:
![]() ;
;
![]() ;
;
4) Вычеркиваем в транспортной таблице строку или столбец с нулевым объемом производства или потребления:
если ![]() – вычеркиваем
– вычеркиваем
![]() -тую
строку;
-тую
строку;
если ![]() – вычеркиваем
– вычеркиваем
![]() -тый
столбец;
-тый
столбец;
5) Повторяем этот процесс с пункта 1 по 4, пока не будут перечеркнуты все строки или столбцы
В нашем случае это выглядит следующим образом:
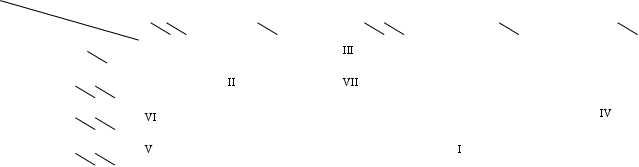 Пища Норы Пища Норы | окорок | мешок крупы | мешок муки | мешок картошки | журналы | |
| 5 2 0 | 18 0 | 17 2 0 | 22 0 | 8 0 | ||
| нора 1 | 15 0 |
|
|
|
|
|
| нора 2 | 20 2 0 |
|
|
|
|
|
| нора 3 | 10 2 0 |
|
|
|
|
|
| нора 4 | 25 3 0 |
|
|
|
|
|
Римскими цифрами пронумерован порядок итераций.
I. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 4 столбец
исключен.
– 4 столбец
исключен.
II. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 2 столбец
исключен.
– 2 столбец
исключен.
III. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 1 строка
исключена.
– 1 строка
исключена.
IV. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 5 столбец
исключен.
– 5 столбец
исключен.
V. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 4 строка
исключена.
– 4 строка
исключена.
VI. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 3 строка
и 1 столбец
исключены.
– 3 строка
и 1 столбец
исключены.
VII. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 2 строка
и 3
столбец исключены.
– 2 строка
и 3
столбец исключены.
Порассуждав таким образом, мыши получили следующий начальный опорный план:
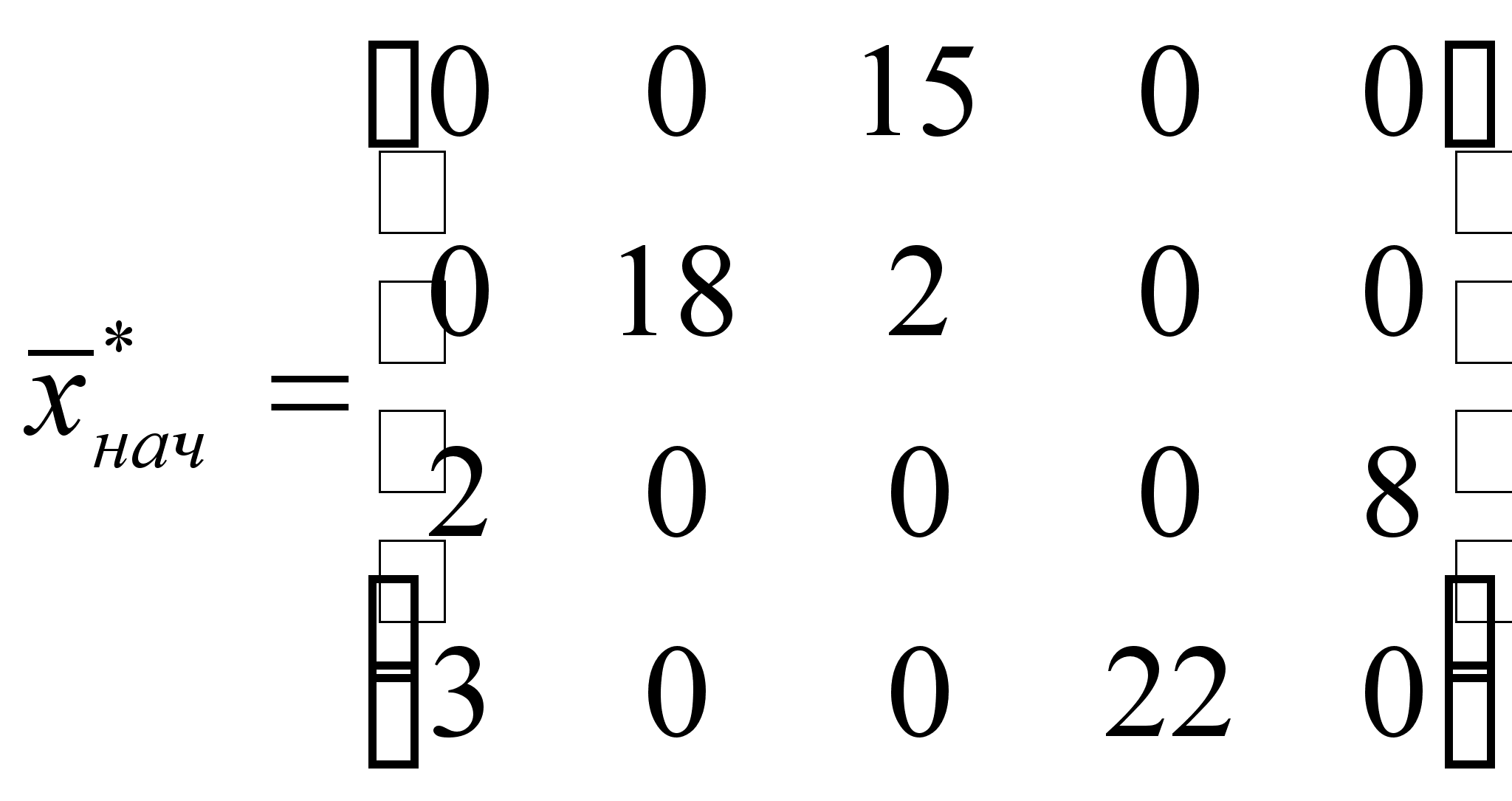 ;
;
![]() .
.
По этому опорному плану коту достанется аж 13 мышей (0,18 часть мыши отдельно вряд ли выживет). “Жирно ему будет”-, подумали мыши и стали составлять другой опорный план методом северо-западного угла.
4. Метод северо-западного угла.
Данный метод
очень прост,
пункты 1 и 2 в методе
максимальной
загрузки заменяются
на следующий:
очередная
загружаемая
коммуникация
![]() выбирается
в левой верхней
клетке сохраненной
части таблицы,
т.е. в северо-западном
углу таблицы.
Математически
это выражается
следующим
образом:
выбирается
в левой верхней
клетке сохраненной
части таблицы,
т.е. в северо-западном
углу таблицы.
Математически
это выражается
следующим
образом:
![]() ,
I – множество
номеров пунктов
производства;
,
I – множество
номеров пунктов
производства;
![]() ,
J – множество
номеров пунктов
потребления;
,
J – множество
номеров пунктов
потребления;
Последовательно по итерациям метода получаем:
I. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 1 столбец
исключен.
– 1 столбец
исключен.
II. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 1 строка
исключена.
– 1 строка
исключена.
III. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 2 столбец
исключен.
– 2 столбец
исключен.
IV. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 2 строка
исключена.
– 2 строка
исключена.
V. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 3 столбец
исключен.
– 3 столбец
исключен.
VI. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 3 строка
исключена.
– 3 строка
исключена.
VII. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 4 столбец
исключен.
– 4 столбец
исключен.
VIII. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 4 строка
и 5 столбец
исключены.
– 4 строка
и 5 столбец
исключены.
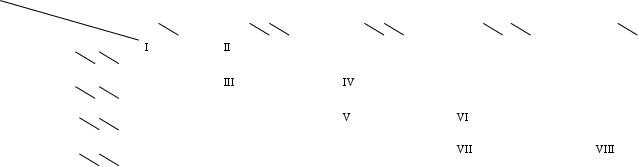 Пища Норы Пища Норы | окорок | мешок крупы | мешок муки | мешок картошки | журналы | |
| 5 0 | 18 8 0 | 17 5 0 | 22 17 0 | 8 0 | ||
| нора 1 | 15 10 0 |
|
|
|
|
|
| нора 2 | 20 12 0 |
|
|
|
|
|
| нора 3 | 10 5 0 |
|
|
|
|
|
| нора 4 | 25 8 0 |
|
|
|
|
|
Получили следующий опорный план:
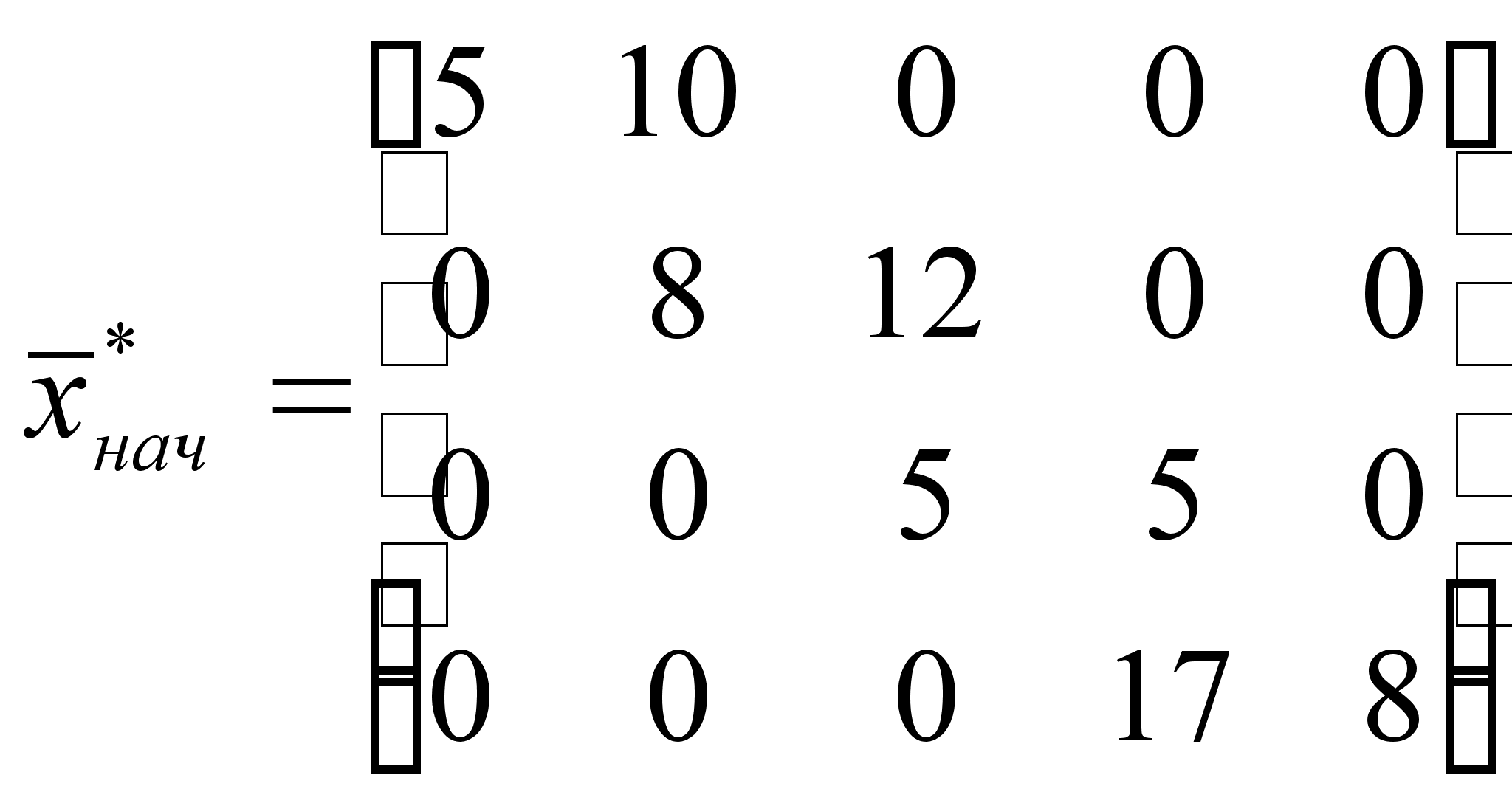 .
.
![]() .
.
Те же самые 13 мышей, и даже хуже предыдущего опорного плана (если учитывать сотые). Пришлось мышам использовать метод минимальных затрат.
5. Метод минимальных затрат.В этом методе в первую очередь загружаются те коммуникации, в которых затраты на перевозку минимальные. В нашем случае, это те пути, мышиные потери на которых минимальны.
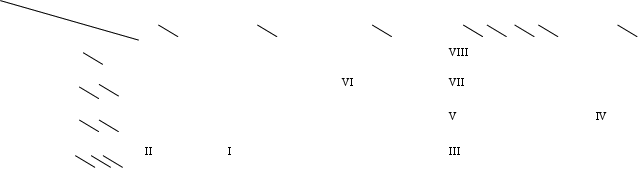 Пища Норы Пища Норы | окорок | мешок крупы | мешок муки | мешок картошки | журналы | |
| 5 0 | 18 0 | 17 0 | 22 20 18 15 0 | 8 0 | ||
| нора 1 | 15 0 |
|
|
|
|
|
| нора 2 | 20 3 0 |
|
|
|
|
|
| нора 3 | 10 2 0 |
|
|
|
|
|
| нора 4 | 25 7 2 0 |
|
|
|
|
|
I. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 2 столбец
исключен.
– 2 столбец
исключен.
II. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 1 столбец
исключен.
– 1 столбец
исключен.
III. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 4 строка
исключена.
– 4 строка
исключена.
IV. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 5 столбец
исключен.
– 5 столбец
исключен.
V. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 3 строка
исключена.
– 3 строка
исключена.
VI. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 3 столбец
исключен.
– 3 столбец
исключен.
VII. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 2 строка
исключена.
– 2 строка
исключена.
VIII. ![]() ;
;
![]() ;
;
![]() ;
;
![]() – 1 строка
и 4 столбец
исключены.
– 1 строка
и 4 столбец
исключены.
Опорный план:
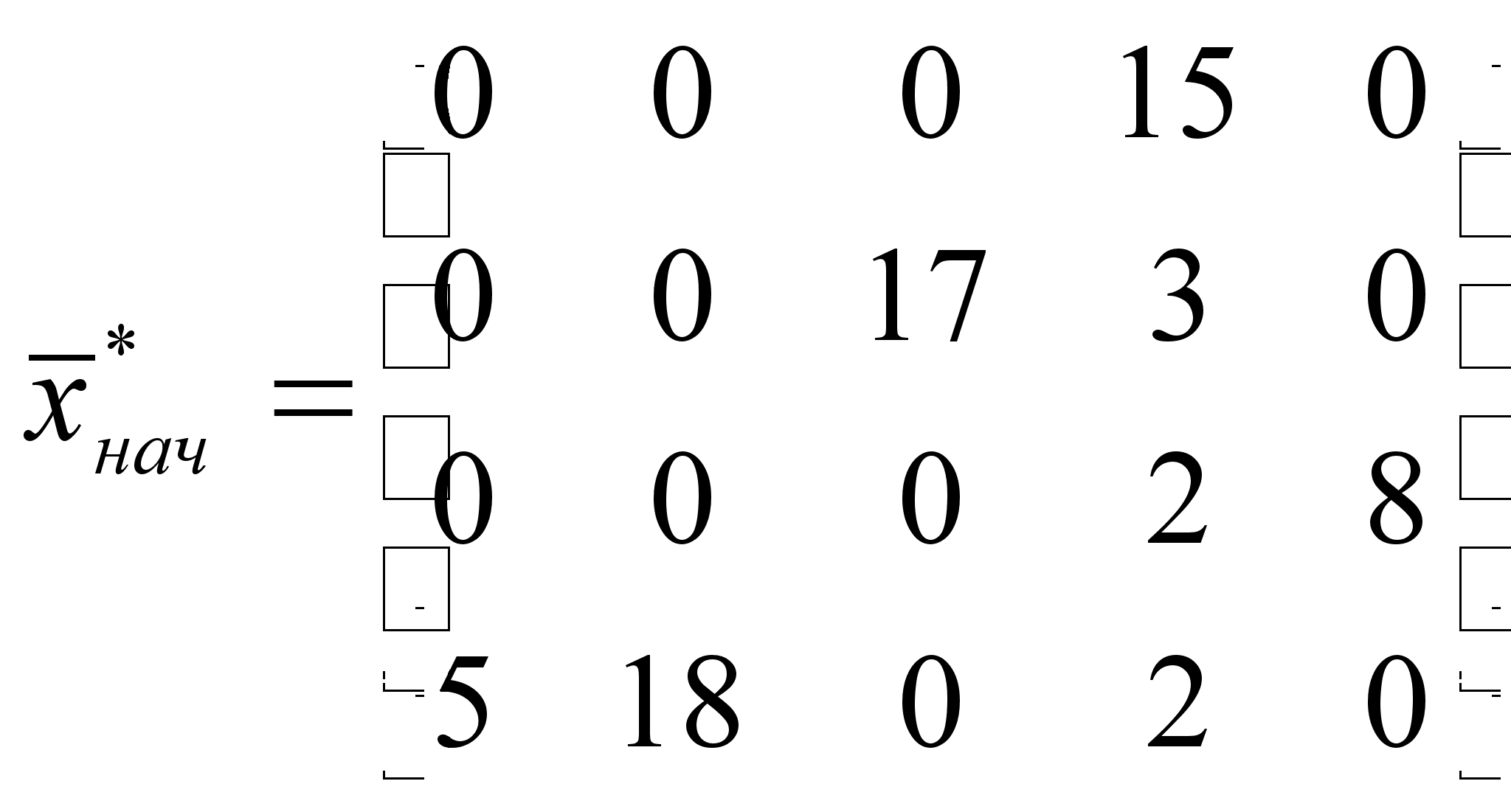
Целевая функция:
![]()
Этот опорный план понравился мышам значительно больше, но все равно потери достаточно велики (7 мышей). Теперь требовалось решить эту задачу и найти оптимальный план. И сделать они это собрались самым точным методом – методом потенциалов.
6. Решение задачи методом потенциалов.Если план действительно оптимален, то система (1) будет выполняться, т.е.:
1) для каждой
занятой клетки
транспортной
таблицы сумма
потенциалов
должна быть
равна ![]() для этой клетки;
для этой клетки;
2) для каждой
незанятой
клетки сумма
потенциалов
не больше (меньше
или равно) ![]() .
.
Построим
для каждой
свободной
переменной
плана числа
![]() и они должны
быть положительны.
Так как число
потенциалов
равно 9, а система
состоит из 8
уравнений, то
для нахождения
какого-либо
решения этой
системы необходимо
первому из
потенциалов
придать произвольное
значение (например:
и они должны
быть положительны.
Так как число
потенциалов
равно 9, а система
состоит из 8
уравнений, то
для нахождения
какого-либо
решения этой
системы необходимо
первому из
потенциалов
придать произвольное
значение (например:
![]() ).
Далее последовательно
находим значения
всех потенциалов.
Распишем подробно
эту процедуру.
).
Далее последовательно
находим значения
всех потенциалов.
Распишем подробно
эту процедуру.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| | окорок | мешок крупы | мешок муки | мешок картошки | журналы | ||
| 5 | 18 | 17 | 22 | 8 | |||
| нора 1 | 15 |
|
|
|
|
|
|
| нора 2 | 20 |
|
|
|
|
|
|
| нора 3 | 10 |
|
|
|
|
|
|
| нора 4 | 25 |
|
|
|
|
|
|
|
|
|
|
|
| |||
Таким образом,
после того, как
все потенциалы
найдены, можно
искать ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Видно, что
![]() и
и ![]() меньше
нуля, значит
существующий
опорный план
можно улучшить.
Поскольку
меньше
нуля, значит
существующий
опорный план
можно улучшить.
Поскольку ![]() ,
нужно ввести
в базис вектор,
соответствующий
клетке (2; 1), для
чего загрузить
ее некоторым
количеством
единиц груза
(мышей). Но, так
как мы, увеличивая
загрузку (2; 1),
нарушаем баланс
строк и столбцов
распределительной
таблицы, то
следует изменить
объемы поставок
в ряде других
занятых клеток.
А чтобы число
базисных переменных
осталось прежним,
необходимо
вывести из
базиса одну
переменную.
Выводится
обычно та переменная,
у которой загрузка
в цикле минимальна.
,
нужно ввести
в базис вектор,
соответствующий
клетке (2; 1), для
чего загрузить
ее некоторым
количеством
единиц груза
(мышей). Но, так
как мы, увеличивая
загрузку (2; 1),
нарушаем баланс
строк и столбцов
распределительной
таблицы, то
следует изменить
объемы поставок
в ряде других
занятых клеток.
А чтобы число
базисных переменных
осталось прежним,
необходимо
вывести из
базиса одну
переменную.
Выводится
обычно та переменная,
у которой загрузка
в цикле минимальна.
Строим цикл:
(2; 1) – начальная точка цикла;
Что характерно, для этой точки (впрочем как и для других) мы можем построить только один цикл. Каждой клетке цикла приписываем определенный знак:
(2; 1) – “+”, (4; 1) – “-”, (4; 4) – “+” (2; 4) – “-”.
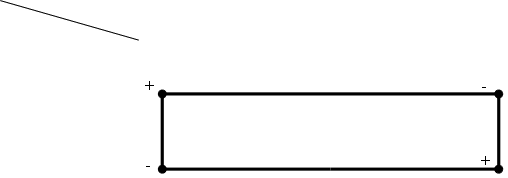 Пища Норы Пища Норы | окорок | мешок крупы | мешок муки | мешок картошки | журналы | |
| 5 | 18 | 17 | 22 | 8 | ||
| нора 1 | 15 |
|
|
|
|
|
| нора 2 | 20 |
|
|
|
|
|
| нора 3 | 10 |
|
|
|
|
|
| нора 4 | 25 |
|
|
|
|
|
В клетках с “+” – увеличиваем загрузку, а в клетках с “-” – уменьшаем. Величина, на которую увеличиваем или уменьшаем всегда одна и она определяется из условия:
![]() ,
где
,
где ![]() –
содержимое
клеток с “-”.
–
содержимое
клеток с “-”.
Таким образом получаем:
![]() ,
а значит из
базиса будет
выведена (2;
4), где в процессе
реализации
цикла загрузка
уменьшится
до 0.
,
а значит из
базиса будет
выведена (2;
4), где в процессе
реализации
цикла загрузка
уменьшится
до 0.
Перейдем к новому опорному плану
| | окорок | мешок крупы | мешок муки | мешок картошки | журналы | ||
| 5 | 18 | 17 | 22 | 8 | |||
| нора 1 | 15 |
|
|
|
|
|
|
| нора 2 | 20 |
|
|
|
|
|
|
| нора 3 | 10 |
|
|
|
|
|
|
| нора 4 | 25 |
|
|
|
|
|
|
|
|
|
|
|
| |||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определяем
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Все ![]() больше 0, следовательно
план оптимальный.
больше 0, следовательно
план оптимальный.
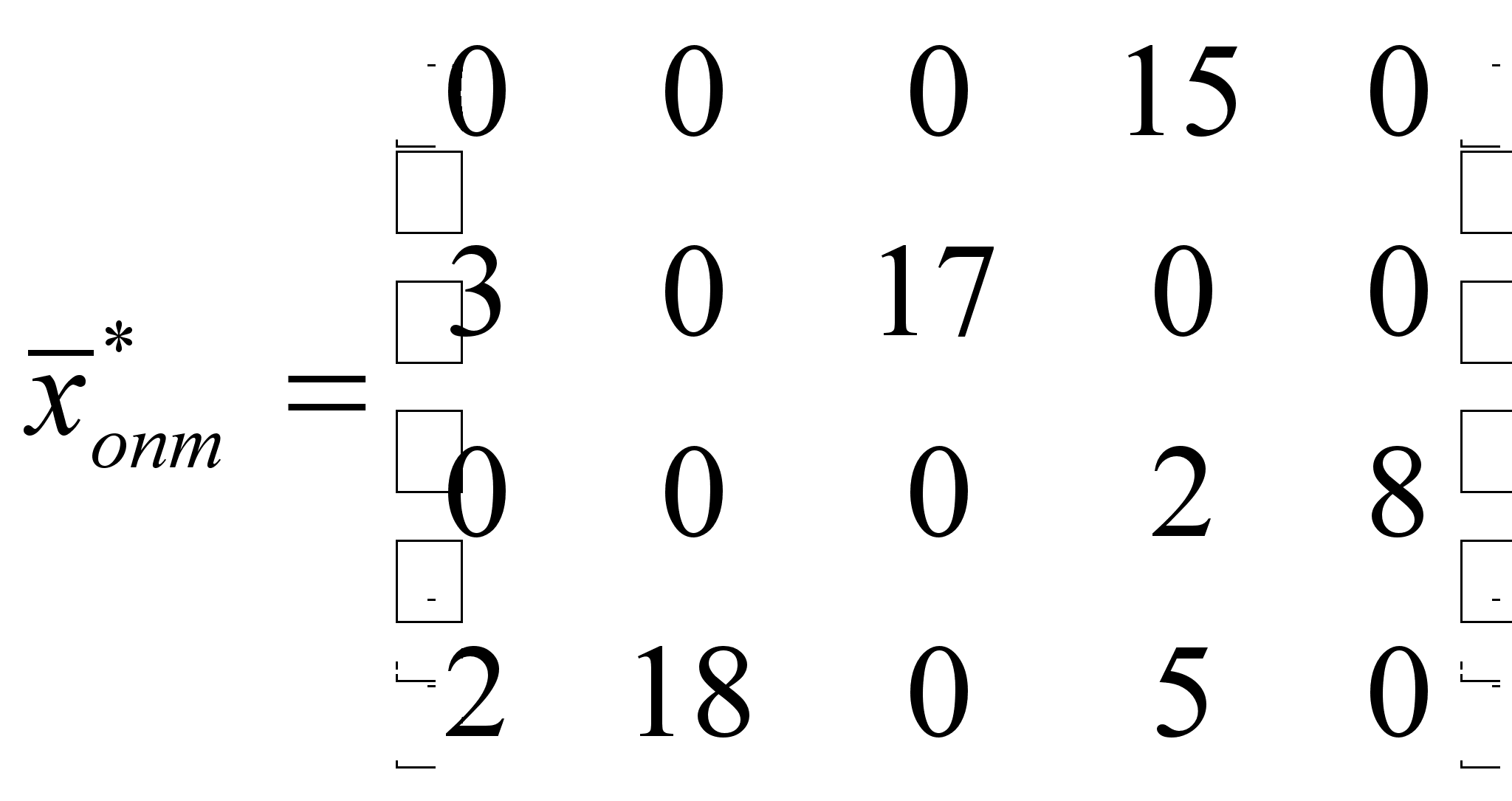 .
.
Целевая функция при этом плане:
![]()
М-да, незначительное улучшение для мышей. Целых 6 мышей и еще один мышиный хвостик – такова ежедневная дань коту Василию. Но делать нечего, и стали мыши действовать по этому плану.
7. Открытая модель.И все было бы хорошо, но в 3 норе появился дополнительный приплод – 10 мышей, следовательно в ней стало проживать 20 мышей, а количество мышей, питающихся у источников пищи, осталось тем же. Получилась так называемая открытая модель, где:
![]() (3)
(3)
и
ее необходимо
сбалансировать.
Для этого нужно
ввести фиктивный
пункт потребления
![]() с объемом
потребления:
с объемом
потребления:
![]() ;
;
и
дополнительные
переменные
![]() приводящие
ограничение-неравенство
(3) к виду равенств
и понимание
как фиктивные
перевозки из
пунктов производства
в фиктивный
пункт потребления.
Новая математическая
модель:
приводящие
ограничение-неравенство
(3) к виду равенств
и понимание
как фиктивные
перевозки из
пунктов производства
в фиктивный
пункт потребления.
Новая математическая
модель:

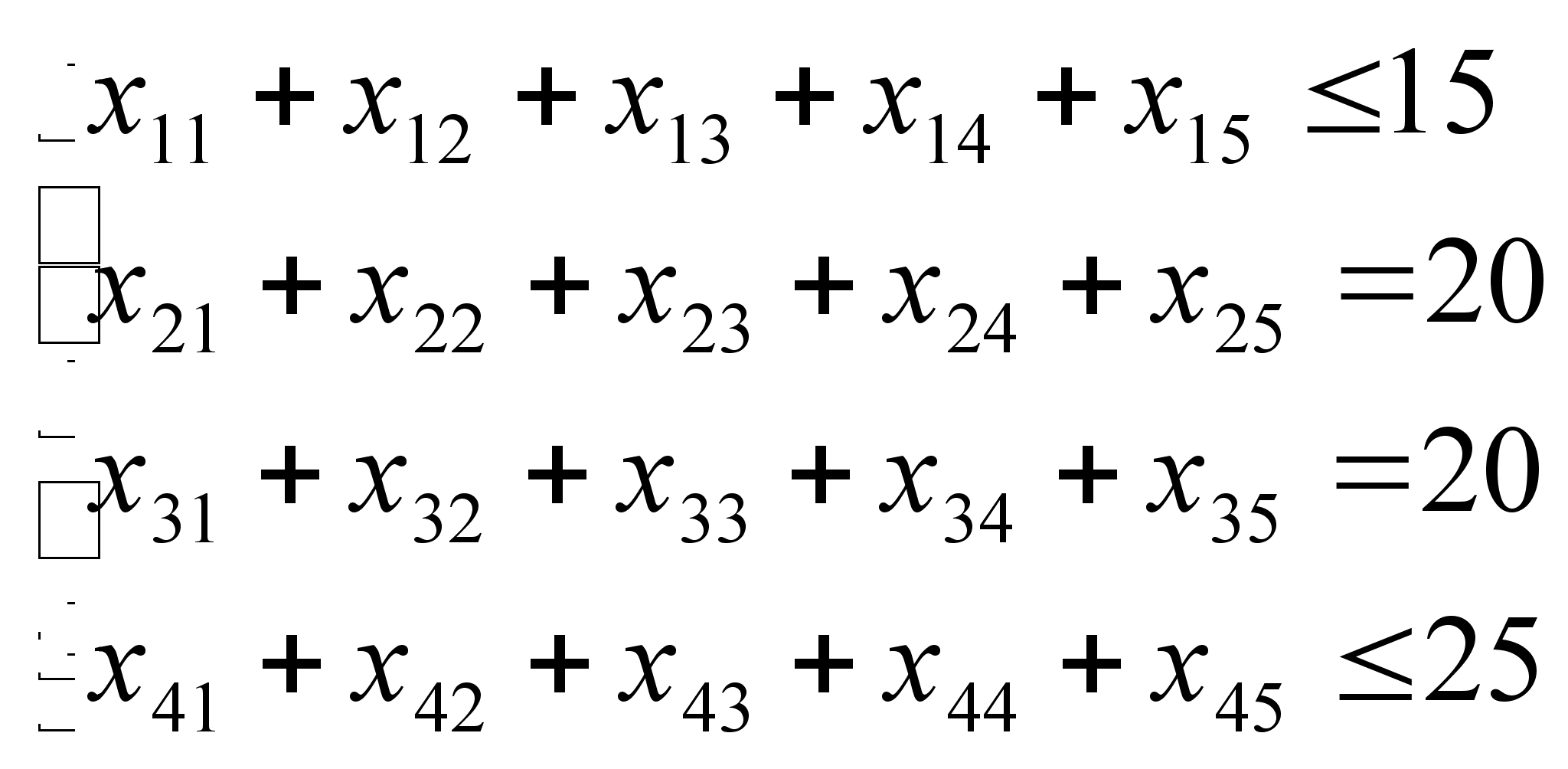 ;
; 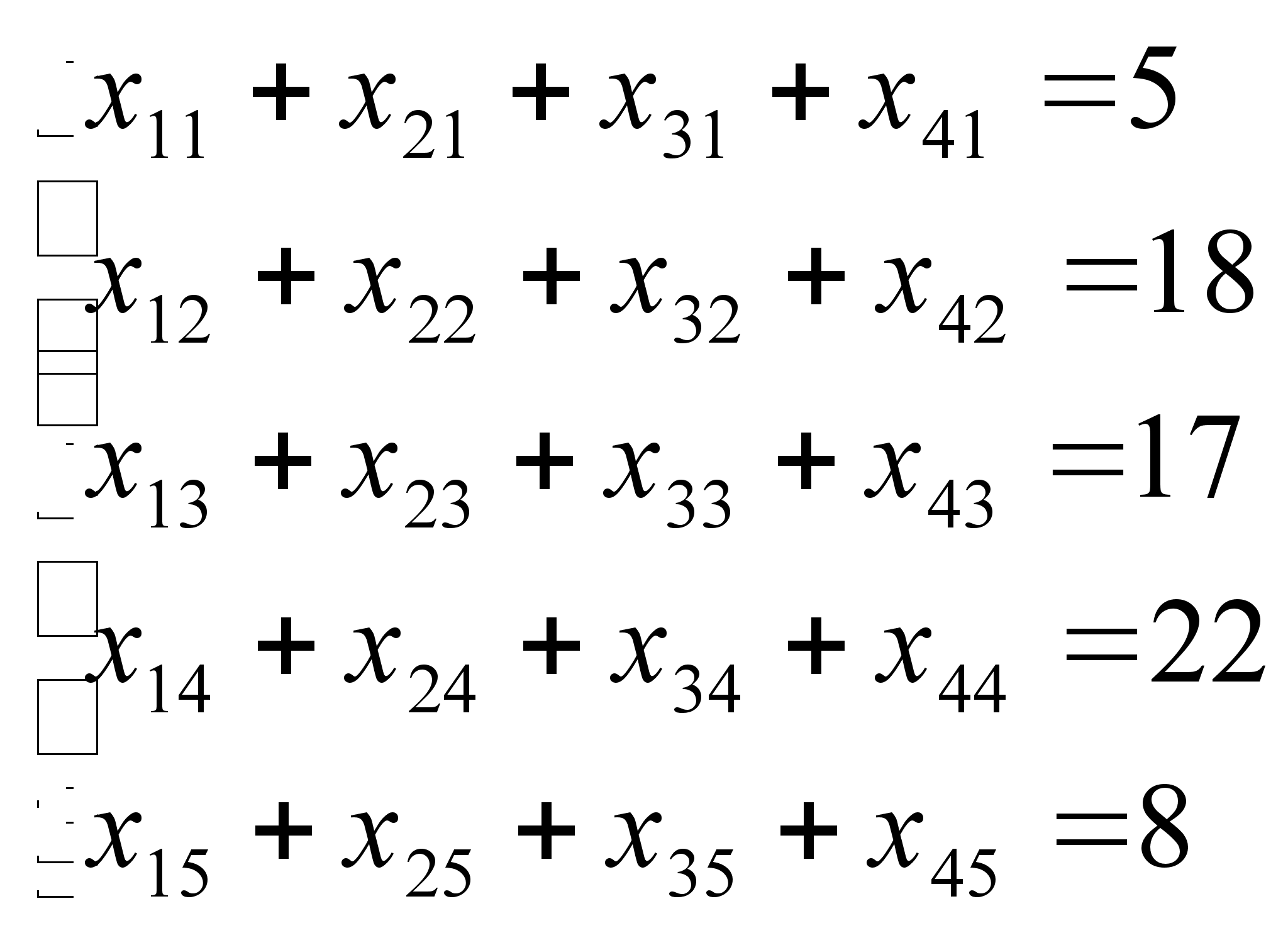 ;
; ![]()
При этом во 2 и 3 норах все мыши должны быть накормлены (во второй – самые умные мыши, а в третьей – большой приплод), поэтому второе и третье ограничения – уравнения. В первое и четвертое ограничения добавим новые переменные R1 и R4 для уравновешивания системы. А так как этих источников пищи на самом деле нет, то и затраты (потери по дороге) на них нулевые.
В транспортной таблице в последнем столбце введем еще 2 переменные в (2; 5) и (3; 5) – R2 и R3 , чтобы столбец был полностью заполнен, а так как перевозки в этих коммуникациях не должны быть, то наложим на них очень большие штрафы М и включим все новые переменные в целевую функцию:
![]()
Так как критерий
стремится к
минимуму, то
в оптимальном
плане перевозки
с самыми большими
затратами не
должны осуществляться
(т.е. ![]() ).
Напишем новую
транспортную
таблицу и найдем
начальный
опорный план
методом минимальных
затрат.
).
Напишем новую
транспортную
таблицу и найдем
начальный
опорный план
методом минимальных
затрат.
 Пища Норы Пища Норы | окорок | мешок крупы | мешок муки | мешок картошки | журналы | R | ||
| 5 0 | 18 15 0 | 17 0 | 22 10 0 | 8 0 | 10 5 0 | |||
| нора 1 | 15 5 | | | | | | | |
| нора 2 | 20 3 0 | | | | | | | |
| нора 3 | 20 12 0 | | | | | | | |
| нора 4 | 25 10 5 0 | | | | | | | |
| | | | | | | |||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определяем
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() меньше 0, поэтому
существующий
опорный план
можно улучшить.
Поскольку
меньше 0, поэтому
существующий
опорный план
можно улучшить.
Поскольку ![]() –
наибольший,
то мы будем
вводить в базис
вектор, соответствующий
клетке (4; 4). Строим
цикл и
переходим к
новому опорному
плану.
–
наибольший,
то мы будем
вводить в базис
вектор, соответствующий
клетке (4; 4). Строим
цикл и
переходим к
новому опорному
плану.
 Пища Норы Пища Норы | окорок | мешок крупы | мешок муки | мешок картошки | журналы | R | ||
| 5 | 18 | 17 | 22 | 8 | 10 | |||
| нора 1 | 15 | | | | | | | |
| нора 2 | 20 | | | | | | | |
| нора 3 | 20 | | | | | | | |
| нора 4 | 25 | | | | | | | |
| | | | | | | |||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определяем
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() меньше 0, поэтому
существующий
опорный план
можно также
улучшить. Теперь
мы будем вводить
в базис вектор,
соответствующий
клетке (2; 1). Строим
цикл и
переходим к
новому опорному
плану.
меньше 0, поэтому
существующий
опорный план
можно также
улучшить. Теперь
мы будем вводить
в базис вектор,
соответствующий
клетке (2; 1). Строим
цикл и
переходим к
новому опорному
плану.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| | окорок | мешок крупы | мешок муки | мешок картошки | журналы | R | ||
| 5 | 18 | 17 | 22 | 8 | 10 | |||
| нора 1 | 15 | | | | | | | |
| нора 2 | 20 | | | | | | | |
| нора 3 | 20 | | | | | | | |
| нора 4 | 25 | | | | | | | |
| | | | | | | |||
Определяем
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Все ![]() больше 0, следовательно
план оптимальный.
больше 0, следовательно
план оптимальный.
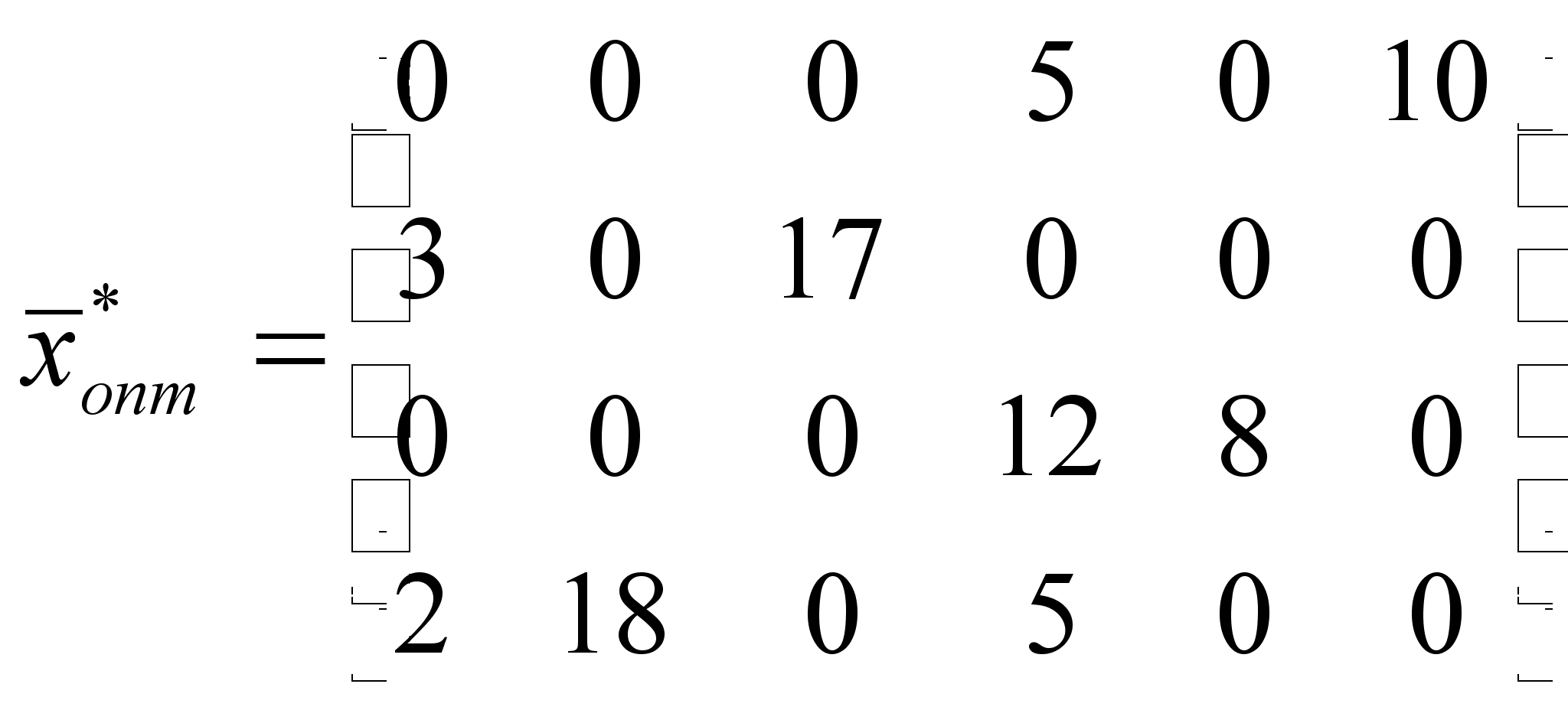 .
.
Целевая функция при этом плане:
![]()
Этот план чуть хуже предыдущего, к тому же 10 мышей из первой норы остаются голодными. Во всяком случае питаются раз в три дня.
8. Запрещенные перевозки.Но кот Василий тоже не дремал, и, произведя те же операции, что и мыши в свое время, определил оптимальный план их передвижений (см. пункт 6). Посмотрев на него, он сразу решил взять под особый контроль путь от второй норы к мешку муки и от четвертой норы к мешку крупы.
Вскоре мыши это на себе почувствовали, а почувствовав, кинулись составлять новый оптимальный план, пометив эти два маршрута как чрезвычайно опасные буквой М
| | окорок | мешок крупы | мешок муки | мешок картошки | журналы | ||
| 5 | 18 | 17 | 22 | 8 | |||
| Нора 1 | 15 |
|
|
|
|
|
|
| Нора 2 | 20 |
|
|
|
|
|
|
| Нора 3 | 10 |
|
|
|
|
|
|
| Нора 4 | 25 |
|
|
|
|
|
|
|
|
|
|
|
| |||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Видно, что этот план уже является оптимальным.
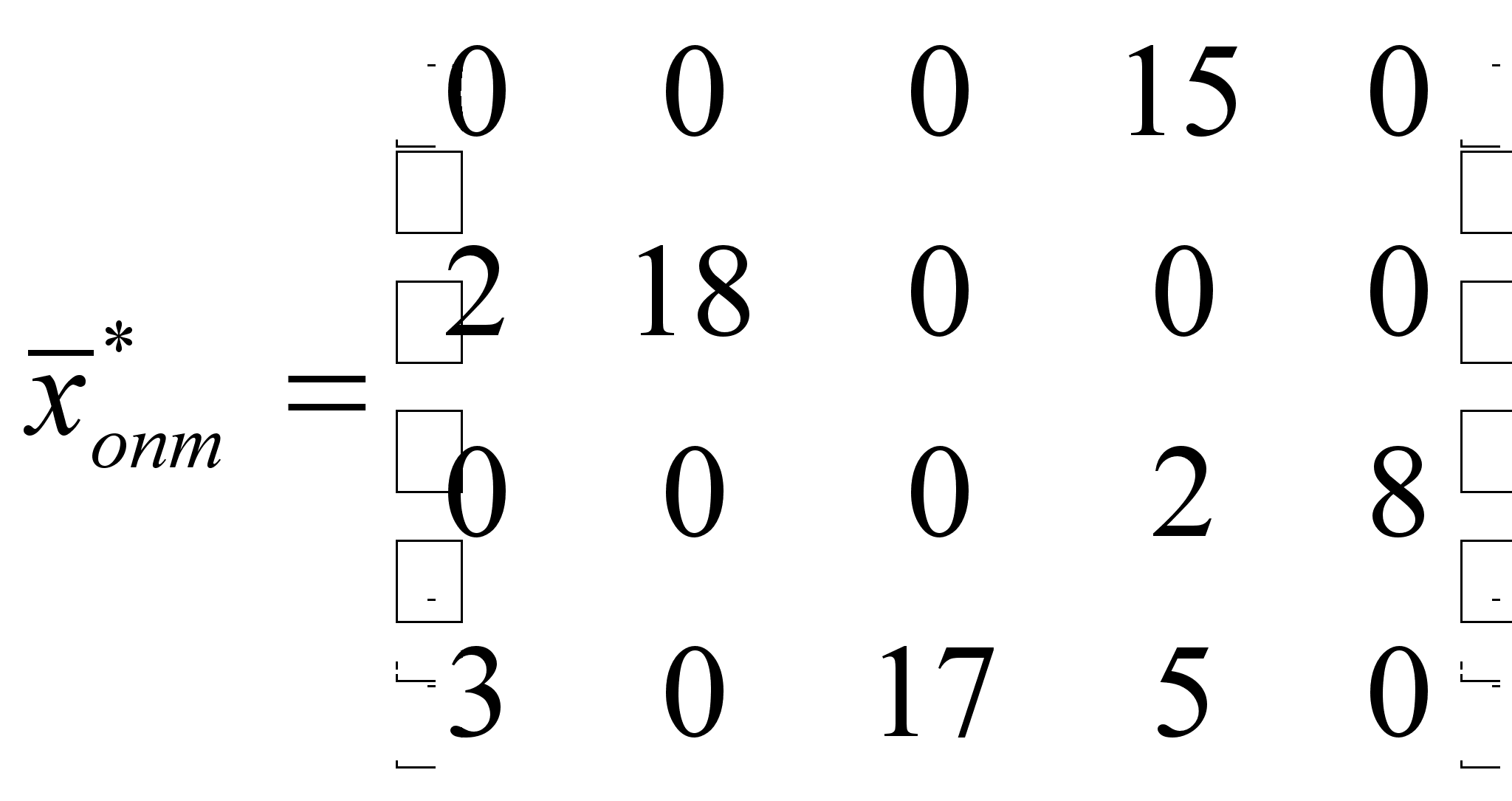
Целевая функция:
![]() .
.
Как зыбко мышиное счастье. Стоило коту взяться за дело всерьез, и потери возросли чуть ли не в два раза.
10
Лабораторная работа № 6
Телешовой Елизаветы, гр. 726,
Решение задачи о ранце методом ветвей и границ. 1. Постановка задачи.1929 год. В США великая депрессия, введен сухой закон. Страна просто задыхается без спиртного. В этот сложный момент группа инициативных граждан под руководством Аль Капоне решает помочь родной стране. Ими планируется поставка алкогольной продукции из Ливерпуля в Штаты. Благодарные сограждане из 5 крупных городов США готовы платить большие деньги за тонну спиртного: 2000 долл. в Бостоне, 3000 в Детройте, 2500 в Вашингтоне, 3200 в Нью-Йорке и 1800 долл в Чикаго. Все 5 городов находятся на разном расстоянии от порта, куда прибывает груз: Бостон – 250 миль, Детройт – 300 миль, Вашингтон – 500 миль, Нью-Йорк –100 миль и Чикаго – 600 миль. Требуется выбрать города, в которых можно получить максимальную прибыль от продажи спиртного. При этом суммарное расстояние от этих портов до порта с грузом не должно превышать 1000 миль.
2. Решение задачи.Данная задача является задачей о ранце вида:
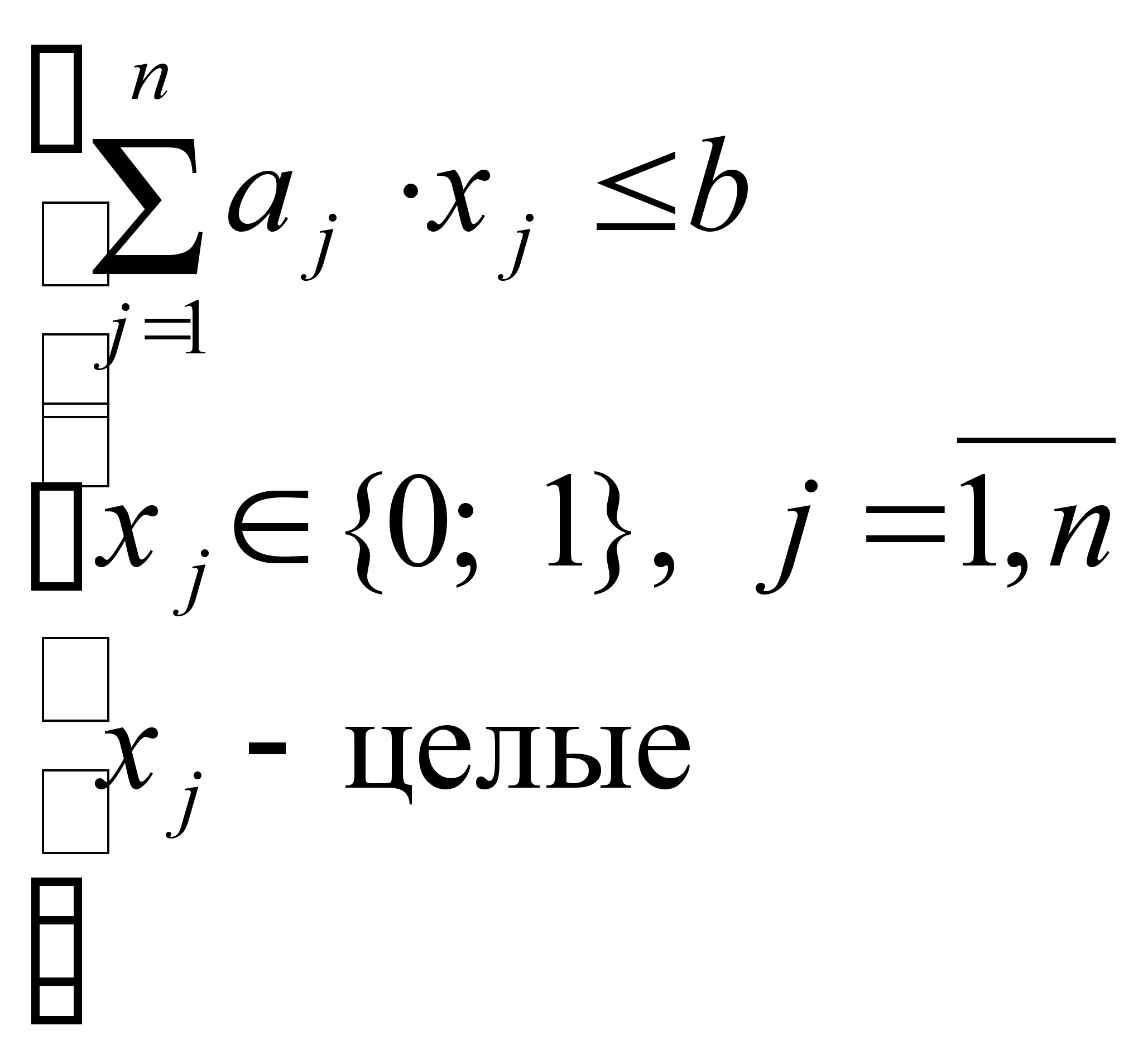 , (1)
, (1)
где критерием является функция
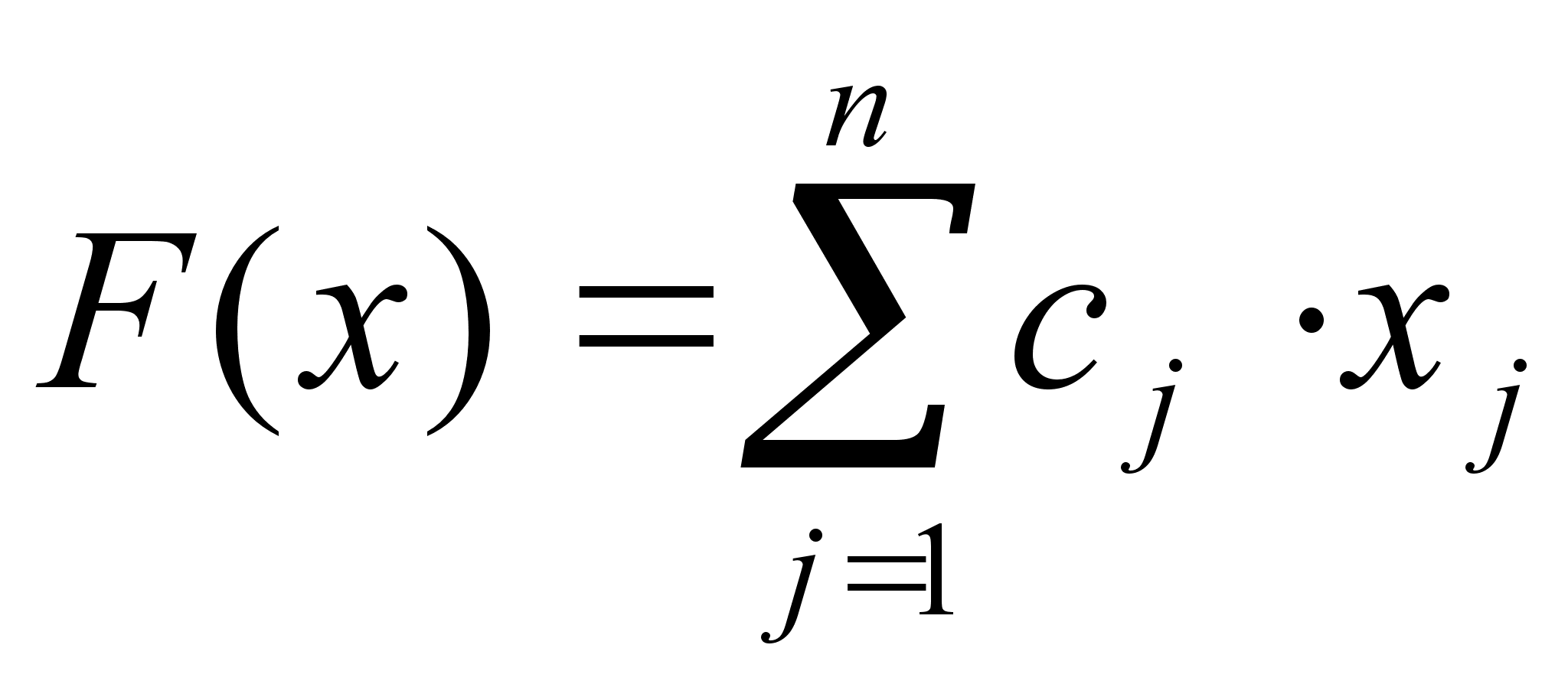 , (2)
, (2)
которая может быть устремлена и к максимуму, и к минимуму.
Для начала составим следующую математическую модель:
Пусть ![]() – j-тый город,
откуда соответственно
– j-тый город,
откуда соответственно
![]() .
При этом, если
в j-тый город
будет разгружаться
алкогольная
продукция, то
.
При этом, если
в j-тый город
будет разгружаться
алкогольная
продукция, то
![]() ,
иначе
,
иначе ![]() .
Другим ограничением
будет являться
суммарное
расстояние
до порта с грузом.
Таким образом:
.
Другим ограничением
будет являться
суммарное
расстояние
до порта с грузом.
Таким образом:
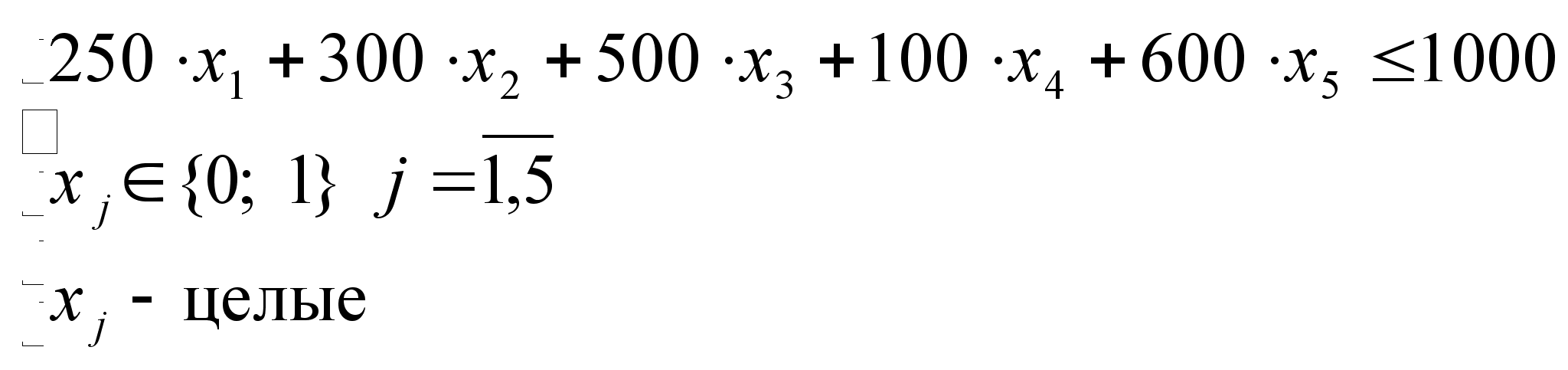 ;
;
Целевой функцией или критерием будет являться максимальная благодарность сограждан:
![]() .
.
Далее
отбираем порты
по приоритетности,
т.е. в порядке
убывания отношения
![]() :
:
![]() (3);
(3); ![]() (2);
(2); ![]() (4);
(4); ![]() (1);
(1); ![]() (5).
(5).
После
этого определяем
начальный план
следующим
образом: пусть
![]() ,
поскольку
отношение
,
поскольку
отношение ![]() наибольшее,
и следовательно
продажа спиртного
в Нью-Йорке
даст наибольшую
прибыль при
наименьших
затратах, которые
зависят от
расстояния.
Вычитая из
суммарного
расстояния
наибольшее,
и следовательно
продажа спиртного
в Нью-Йорке
даст наибольшую
прибыль при
наименьших
затратах, которые
зависят от
расстояния.
Вычитая из
суммарного
расстояния
![]() расстояние
до порта мы
получим расстояние,
которое разделяется
между остальными
городами, т.е.:
расстояние
до порта мы
получим расстояние,
которое разделяется
между остальными
городами, т.е.:
![]() ,
,
![]() ;
;
Аналогично рассуждая, далее получаем:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 500 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
начальный
опорный план:
![]() .
.
Значение
целевой функции:
![]() .
.
Но ![]() обязательно
целое. Поэтому
чтобы определить,
чему все же
равен
обязательно
целое. Поэтому
чтобы определить,
чему все же
равен ![]() :
0 или 1 вычислим
следующие
значения:
:
0 или 1 вычислим
следующие
значения:
![]() ;–
целая часть
критерия при
существующем
опорном плане.
;–
целая часть
критерия при
существующем
опорном плане.
![]() ;–
значение
критерия при
целочисленном
опорном плане,
т.е.
;–
значение
критерия при
целочисленном
опорном плане,
т.е. ![]() .
.
Множество
D, которому
принадлежит
![]() имеет
имеет ![]() ,
,
![]() .
Разделим его
на 2 подмножества,
такие что:
.
Разделим его
на 2 подмножества,
такие что:
![]() ;
;
![]() - здесь
- здесь
![]() .
.
![]() -
здесь
-
здесь ![]() .
.
1) Анализ множества D1.
Поскольку
![]() целевая функция
и ограничения
будут иметь
вид:
целевая функция
и ограничения
будут иметь
вид:
![]()
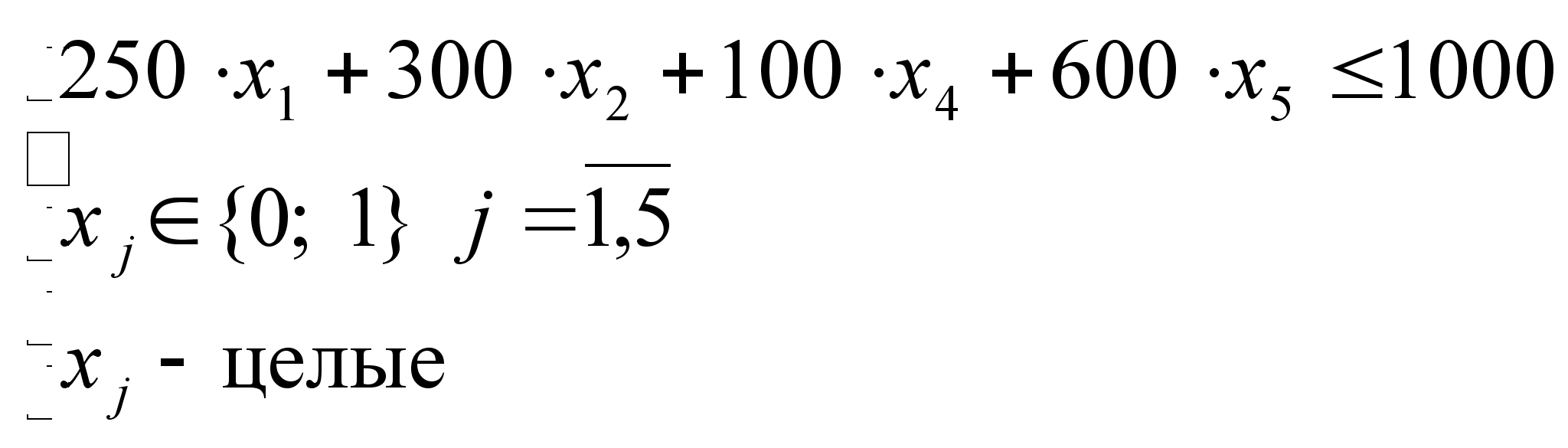
Строим новый опорный план:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
Т.к. ![]() ,
поэтому
,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
![]() ,
при
,
при ![]() .
.
2) Анализ множества D2.
Поскольку
![]() целевая функция
и ограничения
будут иметь
вид:
целевая функция
и ограничения
будут иметь
вид:
![]()
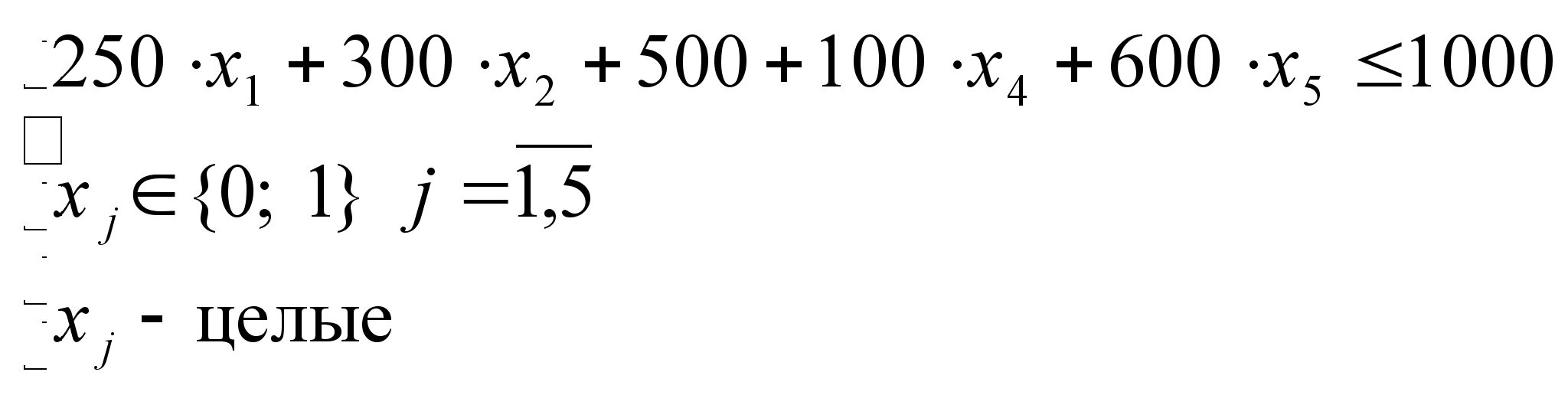 =>
=> 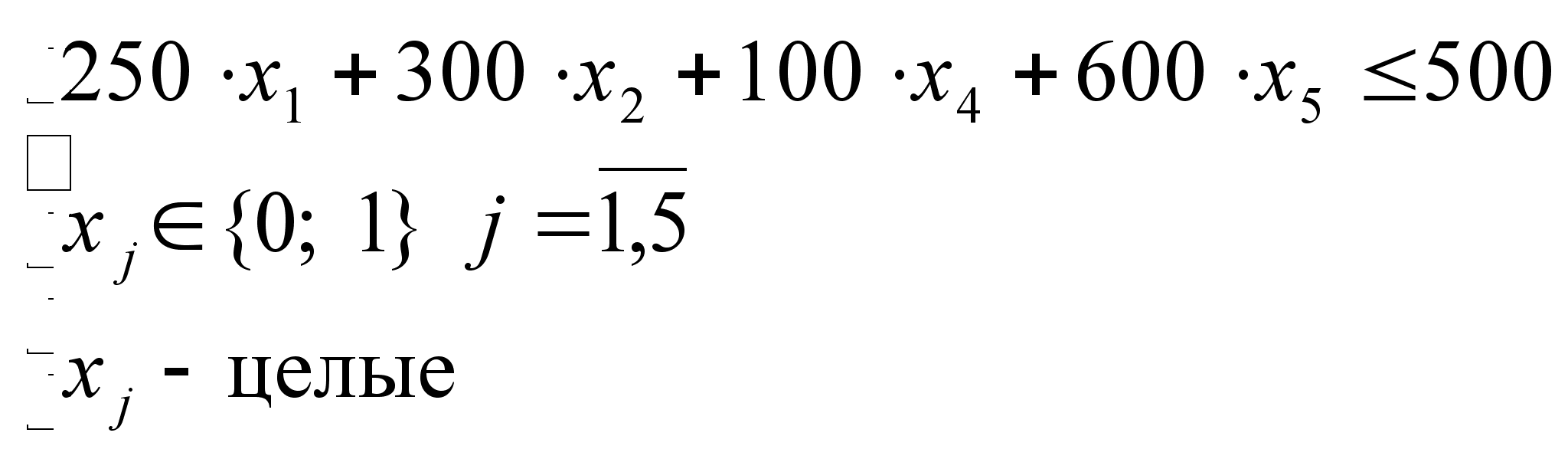 .
.
Строим новый опорный план:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
Т.к. ![]() ,
поэтому
,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
![]() ,
при
,
при ![]() .
.
3) Отсев неперспективного подмножества.
![]() .
.
Так как ![]() и
и ![]() больше Rec,
то оба подмножества
можно считать
перспективными,
но поскольку
больше Rec,
то оба подмножества
можно считать
перспективными,
но поскольку
![]() ,
то далее мы
будем исследовать
подмножество
D2.
Разделим его
на 2 подмножества,
такие что:
,
то далее мы
будем исследовать
подмножество
D2.
Разделим его
на 2 подмножества,
такие что:
![]() ;
;
![]() - здесь
- здесь
![]() .
.
![]() -
здесь
-
здесь ![]() .
.
4) Анализ множества D3.
Поскольку
![]() ,
,
![]() целевая функция
и ограничения
будут иметь
вид:
целевая функция
и ограничения
будут иметь
вид:
![]()
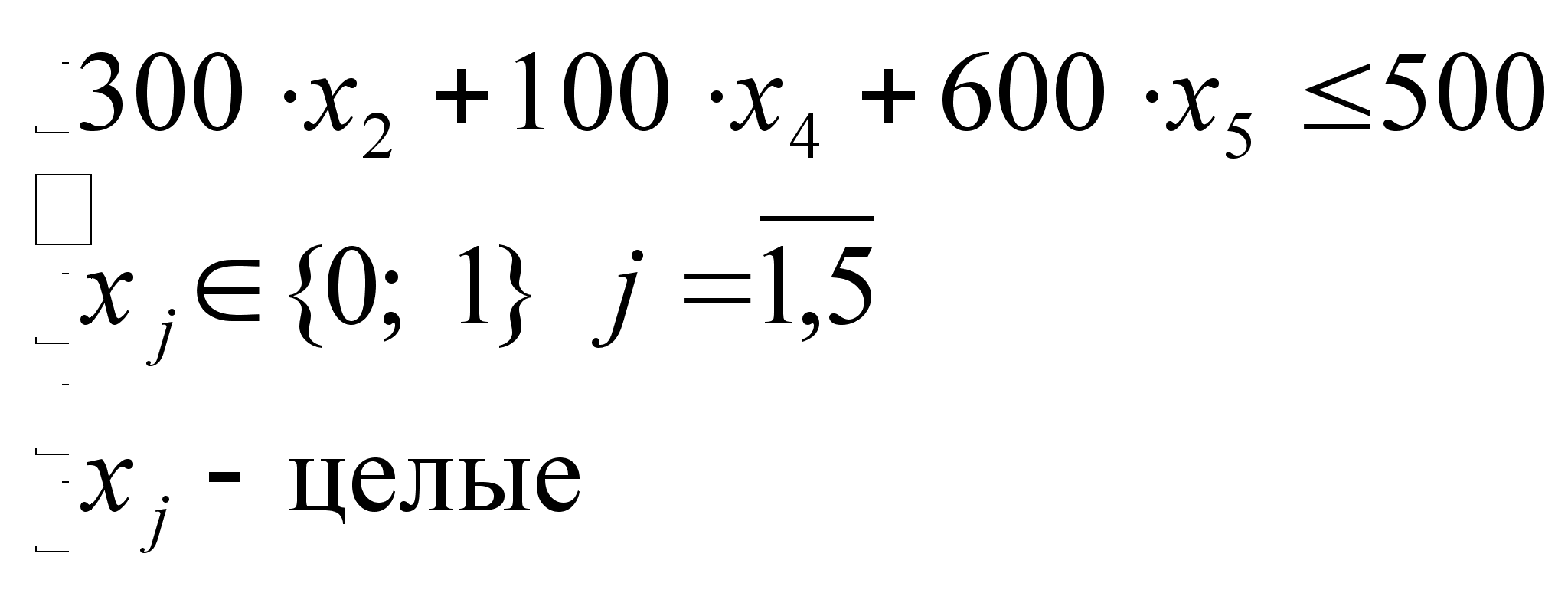 .
.
Строим новый опорный план:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
Т.к. ![]() ,
поэтому
,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
![]() ,
при
,
при ![]() .
.
5) Анализ множества D4.
Поскольку
![]() ,
,
![]() целевая функция
и ограничения
будут иметь
вид:
целевая функция
и ограничения
будут иметь
вид:
![]()
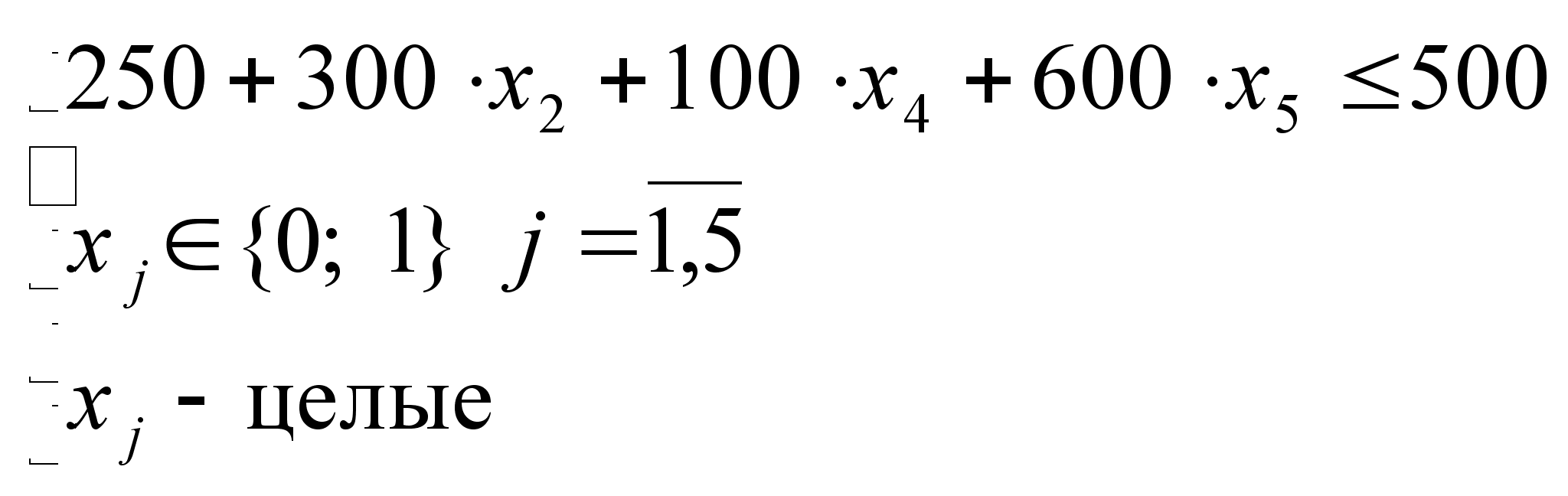 =>
=> 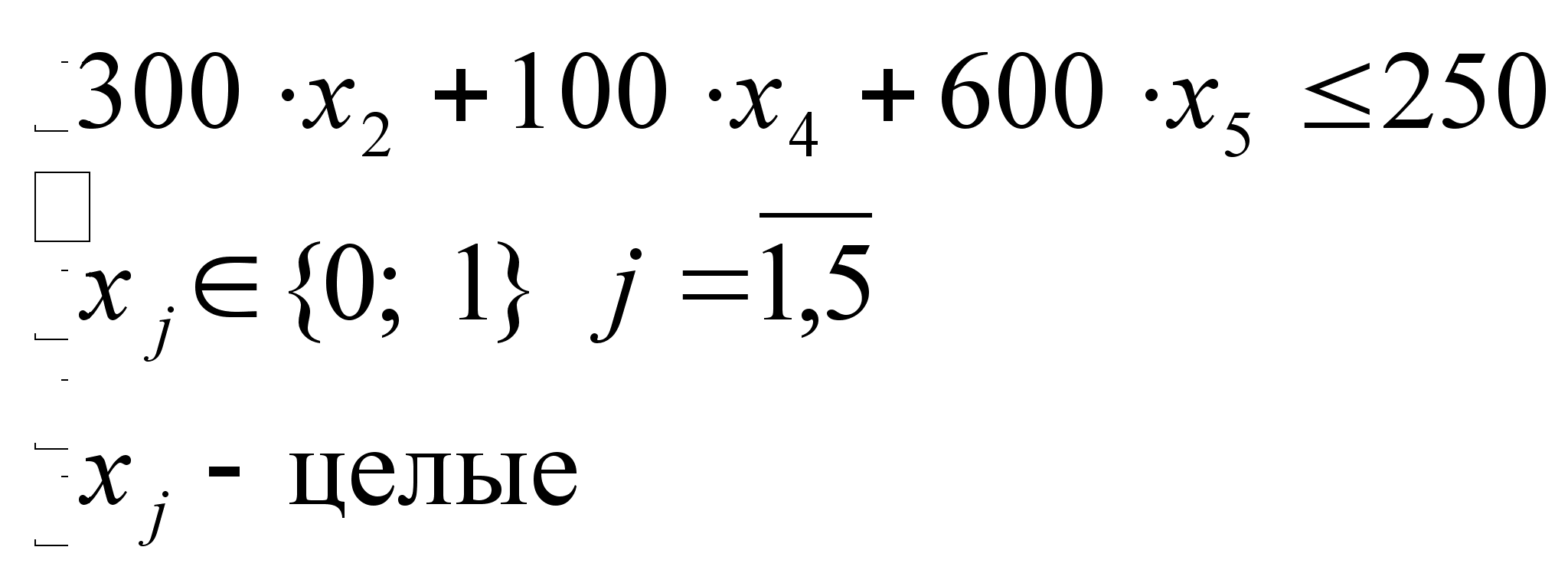 .
.
Строим новый опорный план:
![]() ,
,
![]() ;
;
Т.к. ![]() ,
поэтому
,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
![]() ,
при
,
при ![]() .
.
6) Отсев неперспективного подмножества.
![]() .
.
Так как ![]() и
и ![]() больше Rec,
то оба подмножества
можно считать
перспективными,
но поскольку
больше Rec,
то оба подмножества
можно считать
перспективными,
но поскольку
![]() ,
то далее мы
будем исследовать
подмножество
D3.
Разделим его
на 2 подмножества,
такие что:
,
то далее мы
будем исследовать
подмножество
D3.
Разделим его
на 2 подмножества,
такие что:
![]() ;
;
![]() - здесь
- здесь
![]() .
.
![]() -
здесь
-
здесь ![]() .
.
7) Анализ множества D5.
Поскольку
![]() ,
,
![]() ,
,
![]() целевая функция
и ограничения
будут иметь
вид:
целевая функция
и ограничения
будут иметь
вид:
![]()
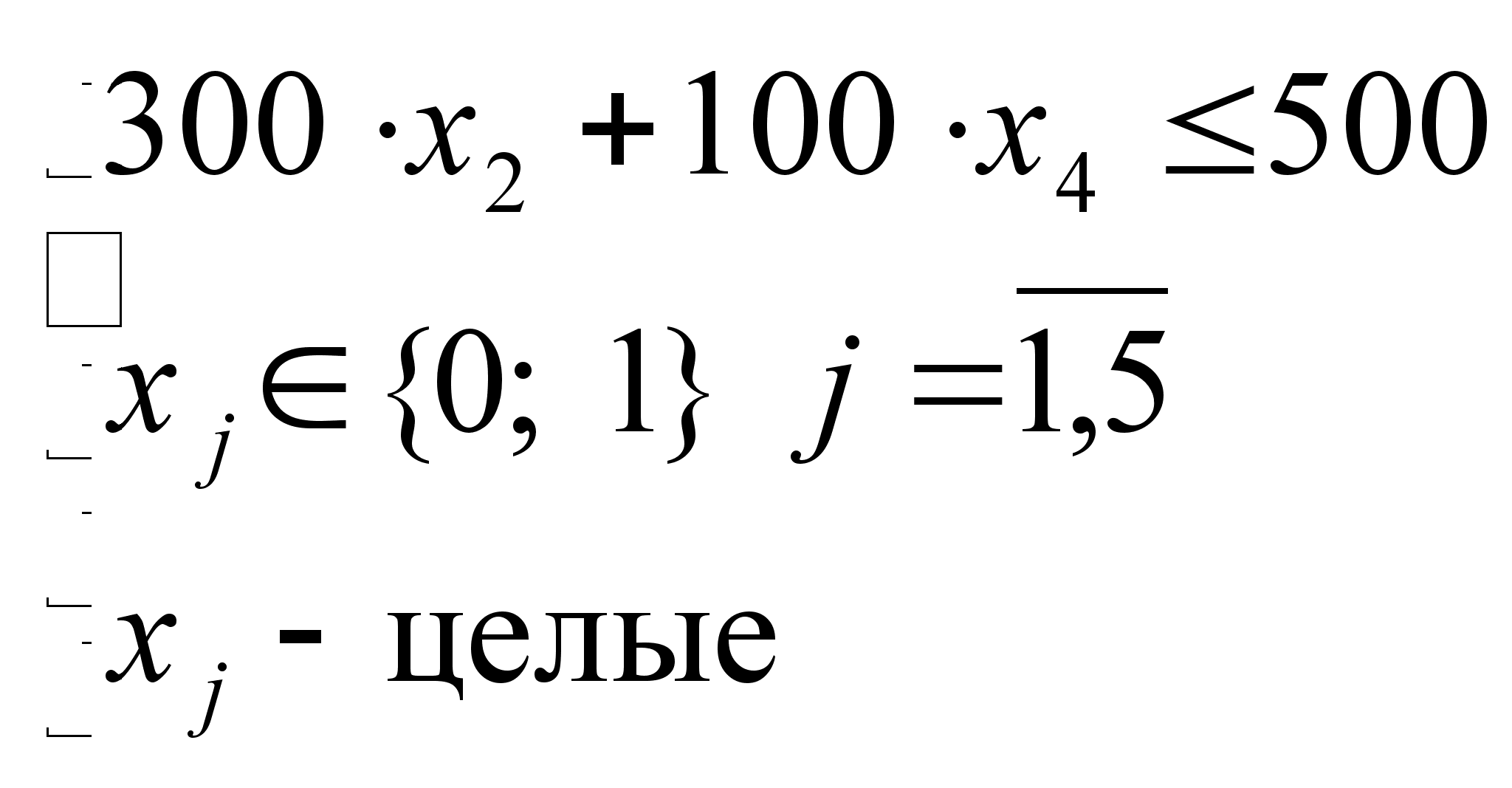 .
.
Строим новый
опорный план,
очевидно: ![]() .
При
.
При ![]() ,
,
![]() ограничение
выполняется
всегда.
ограничение
выполняется
всегда.
![]() ;
;
![]() ,
при
,
при ![]() .
.
8) Анализ множества D6.
Поскольку
![]() ,
,
![]() ,
,
![]() целевая функция
и ограничения
будут иметь
вид:
целевая функция
и ограничения
будут иметь
вид:
![]()
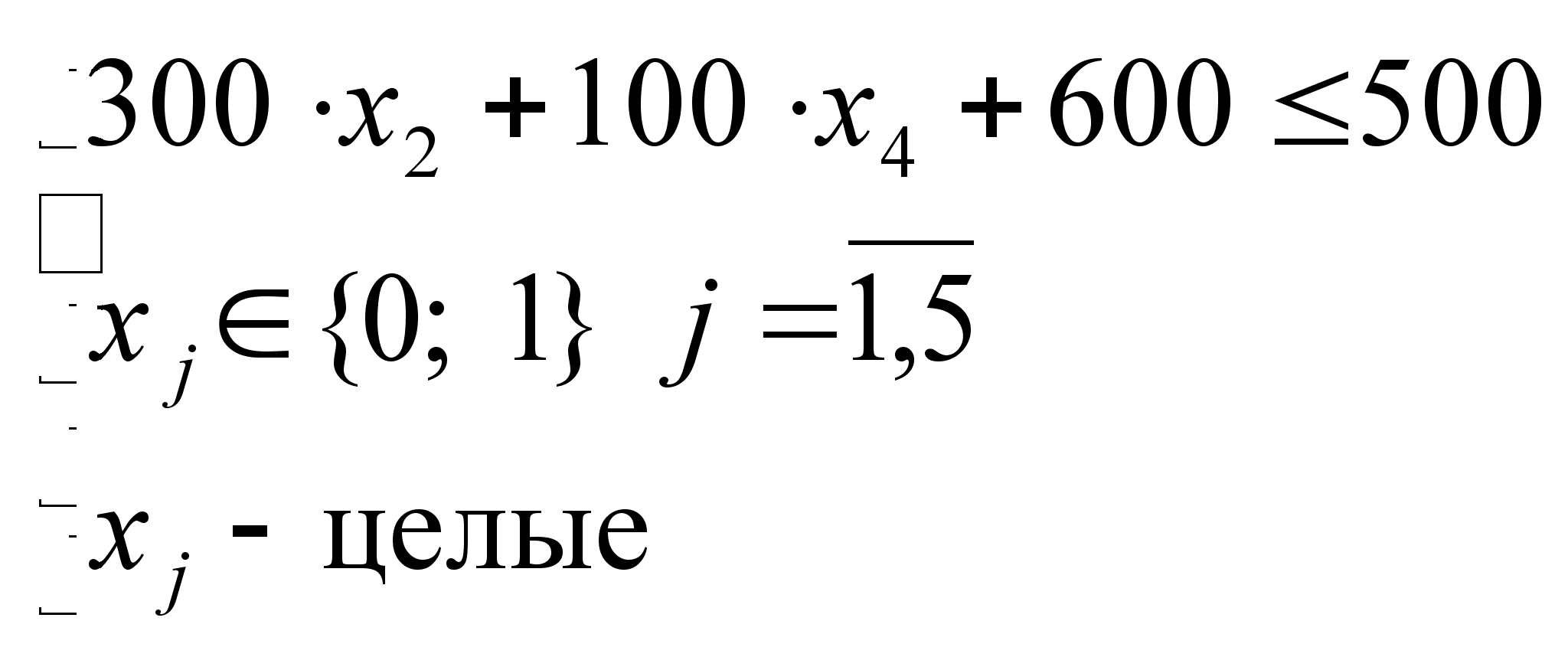
 .
.
Ограничение
несовместное,
поскольку даже
при ![]() оно не выполняется.
Следовательно
множество D6
не существует.
оно не выполняется.
Следовательно
множество D6
не существует.
Таким образом,
оптимальным
планом данной
задачи будет:
![]() ,
то есть алкоголь
выгоднее всего
поставлять
в 3 города: Детройт,
Вашингтон и
Нью-Йорк. При
этом прибыль
составит 8700 долл.
,
то есть алкоголь
выгоднее всего
поставлять
в 3 города: Детройт,
Вашингтон и
Нью-Йорк. При
этом прибыль
составит 8700 долл.
3. Постановка задачи о многомерном ранце.
В связи с тем, что спиртное стало хорошо раскупаться, Аль Капоне решил увеличить поставки. Но чтобы мирно спящее ФБР не дай бог не проснулось, было решено осуществлять поставки через три разных порта на восточном побережье. Цены на спиртное в пяти вышеуказанных городах не изменились, расстояние же от них (в милях) до портов указано в следующей таблице:
| Бостон | Детройт | Вашингтон | Нью-Йорк | Чикаго | |
| Порт 1 | 250 | 300 | 500 | 100 | 600 |
| Порт 2 | 100 | 200 | 700 | 400 | 300 |
| Порт 3 | 500 | 400 | 300 | 550 | 150 |
Во всех трех случаях суммарное расстояние от порта до городов не должно превышать 1000 миль. Требуется решить тот же самый вопрос: в какие города выгоднее поставлять продукцию?
4. Решение задачи о многомерном ранце (вручную).Задача о многомерном ранце имеет следующую математическую модель:
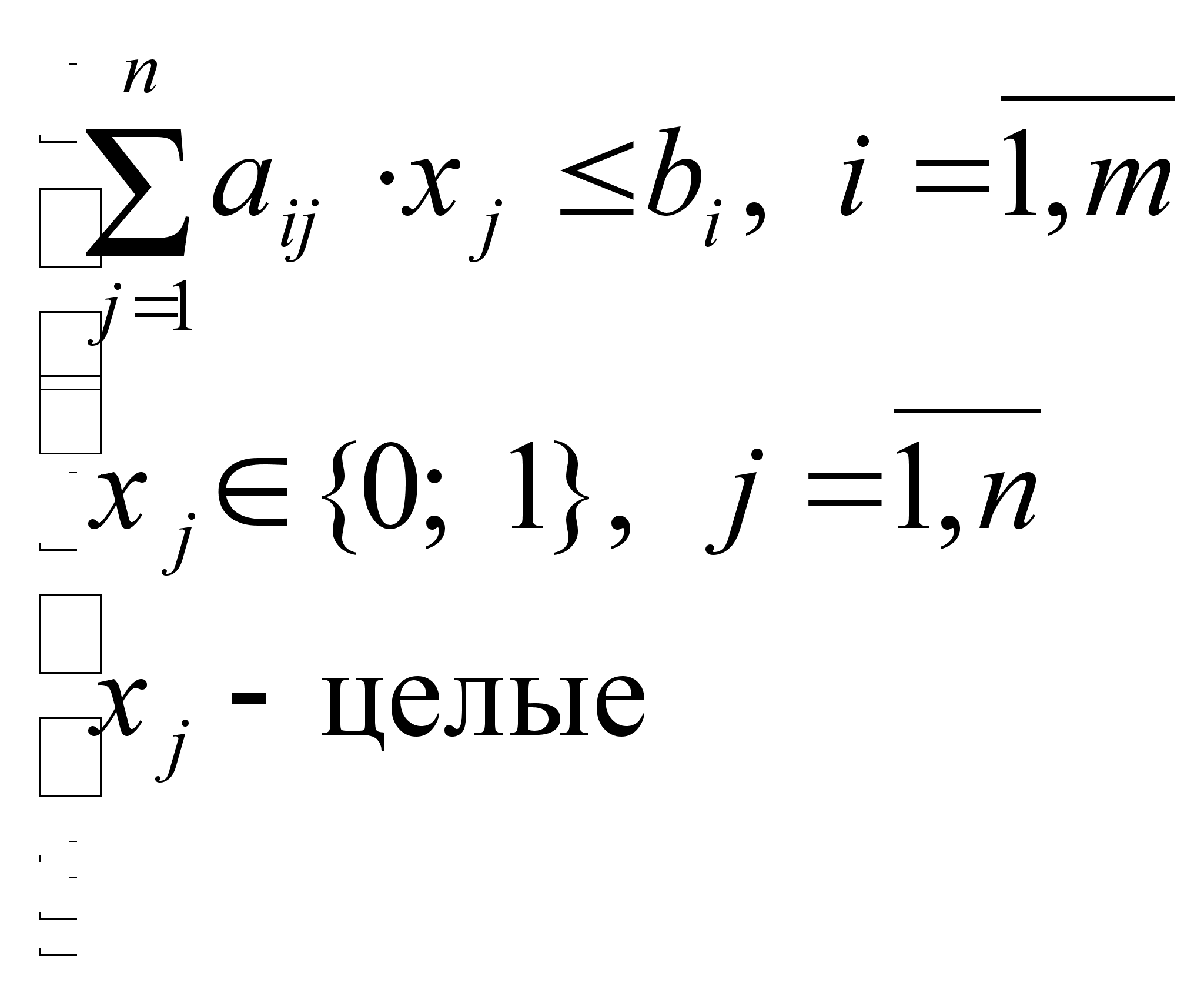 , (3)
, (3)
где критерием является функция
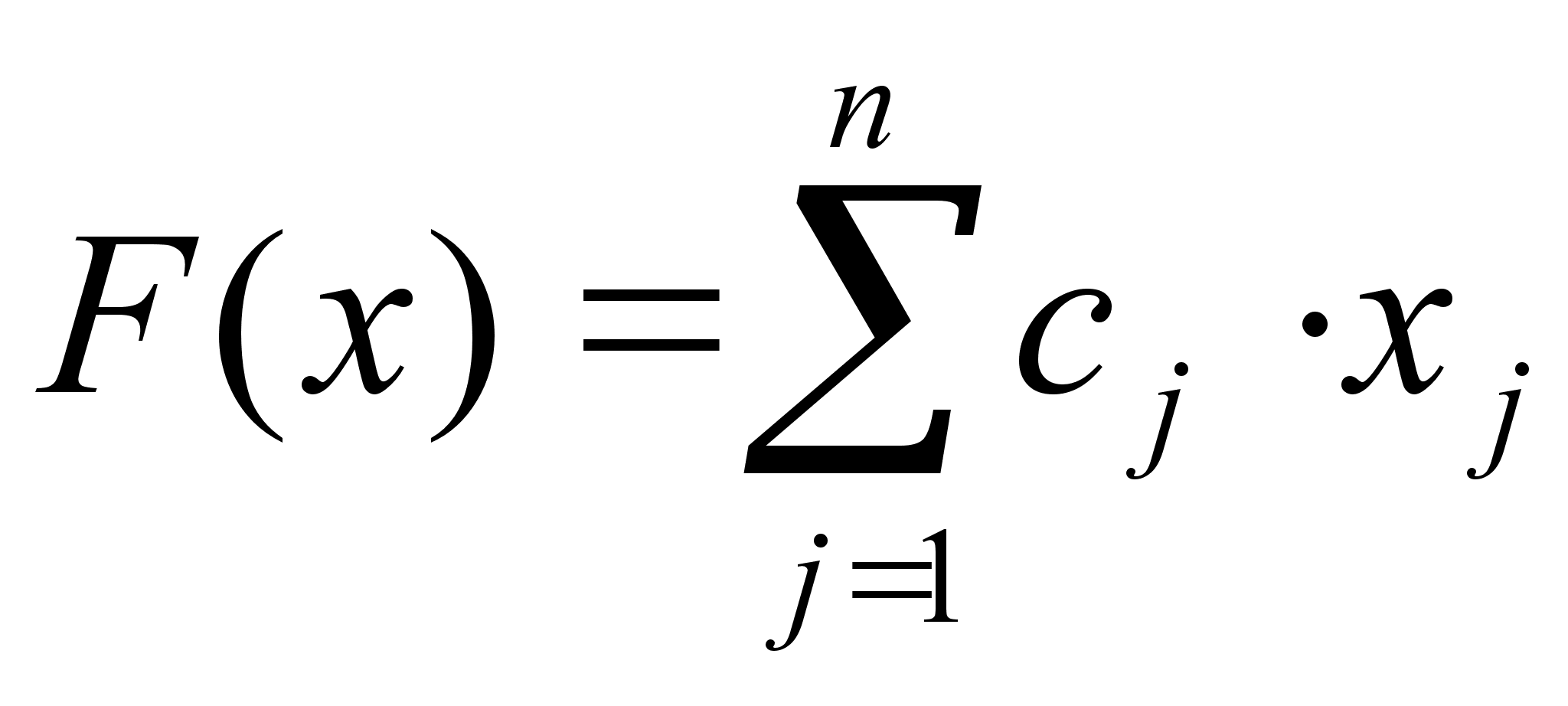 , (4)
, (4)
От задачи об одномерном ранце она отличается наличием нескольких ограничений. Таким образом, математическая модель:
Пусть ![]() – j-тый город,
откуда соответственно
– j-тый город,
откуда соответственно
![]() .
При этом, если
в j-тый город
будет разгружаться
алкогольная
продукция, то
.
При этом, если
в j-тый город
будет разгружаться
алкогольная
продукция, то
![]() ,
иначе
,
иначе ![]() .
.
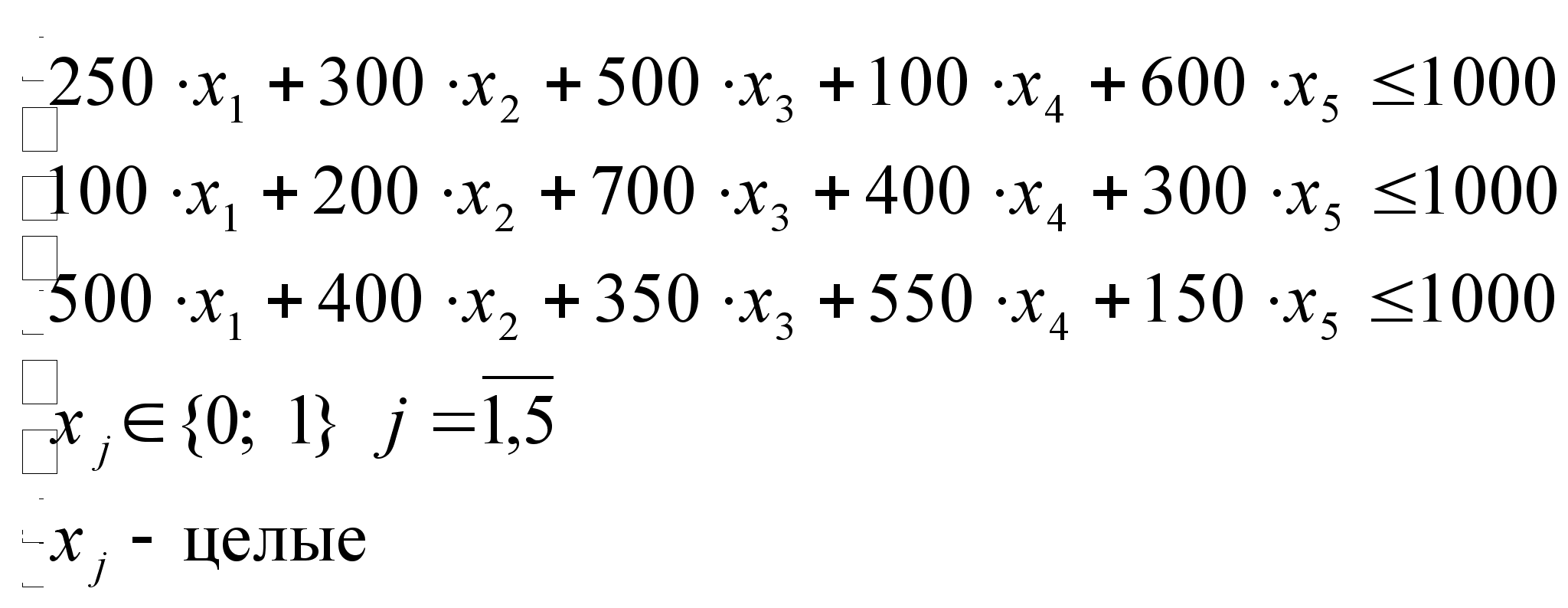 ;
;
Целевой функцией или критерием будет являться максимальная благодарность сограждан:
![]() .
.
Решим
задачу оценки
критерия для
каждого ограничения
в отдельности.
Пусть множество
![]() относится
к первому
ограничению,
относится
к первому
ограничению,
![]() –
ко второму, а
–
ко второму, а
![]() –
к третьему.
–
к третьему.
1) Анализ
множества ![]() .
.
![]() (3);
(3); ![]() (2);
(2); ![]() (4);
(4); ![]() (1);
(1); ![]() (5).
(5).
Определяем начальный план:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 500 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
начальный
опорный план:
![]() .
.
![]() ;
;
2) Анализ
множества ![]() .
.
![]() (1);
(1); ![]() (2);
(2); ![]() (5);
(5); ![]() (3);
(3); ![]() (4).
(4).
Определяем начальный план:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
также равно
300 миль, поэтому
![]() будет целым:
будет целым:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
опорный план:
![]() .
.
![]() ;
;
3) Анализ
множества ![]() .
.
![]() (5);
(5); ![]() (2);
(2); ![]() (3);
(3); ![]() (4);
(4); ![]() (1).
(1).
Определяем начальный план:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 550 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
опорный план:
![]() .
.
![]() ;
;
4) Вычисление верхней и нижней границ.
Вычисляем верхнюю границу:
![]() ;
– третье
ограничение
более жесткое,
далее будем
исследовать
опорный план
;
– третье
ограничение
более жесткое,
далее будем
исследовать
опорный план ![]() .
.
Определяем опорные планы для третьего ограничения:
a) ![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
равно 50 миль,
поэтому ![]() .
Таким образом
:
.
Таким образом
: ![]() .
.
б) ![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
равно 100 миль,
поэтому ![]() .
Таким образом
:
.
Таким образом
: ![]() .
.
в)
В этом случае
![]() .
.
Вычисляем нижнюю границу:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
5) Ветвление множества D.
![]() ;
;
![]() - здесь
- здесь
![]() .
.
![]() -
здесь
-
здесь ![]() .
.
6) Анализ множества D1.
a)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 500 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
б)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 700 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
в)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 100
миль, поэтому
![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
г) Вычисление верхней и нижней границ.
Вычисляем верхнюю границу:
![]() ;
– первое
ограничение
более жесткое.
;
– первое
ограничение
более жесткое.
Определяем опорные планы для первого ограничения:
–
В этом случае
![]() .
.
– ![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
равно 450 миль,
поэтому ![]() .
Таким образом
:
.
Таким образом
: ![]() .
.
– ![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
равно 100
миль, поэтому
![]() .
Таким образом
:
.
Таким образом
: ![]() .
.
Вычисляем нижнюю границу:
Т.к. ![]() ,
то
,
то ![]() ;
;
![]() ;
;
![]() .
.
7) Анализ множества D2.
Поскольку
![]() ,
то:
,
то:
![]() .
.
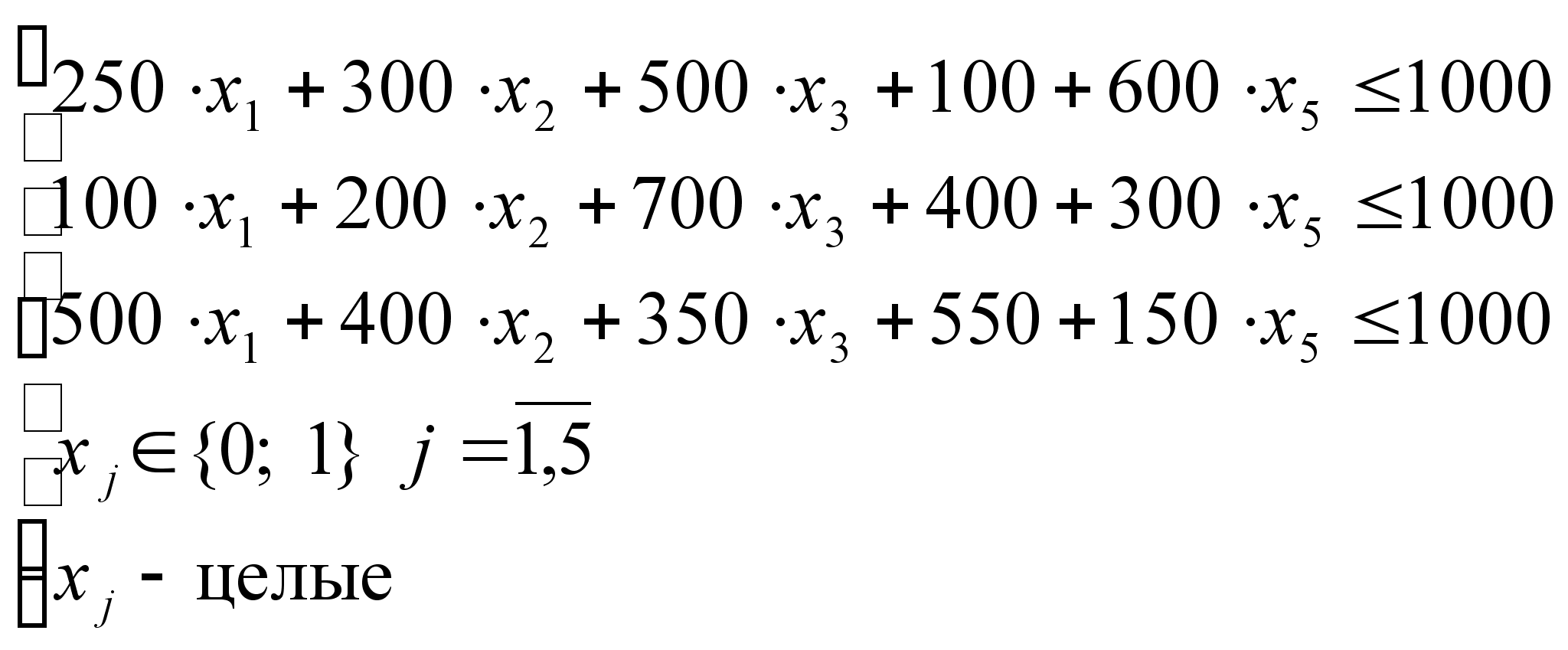 =>
=> 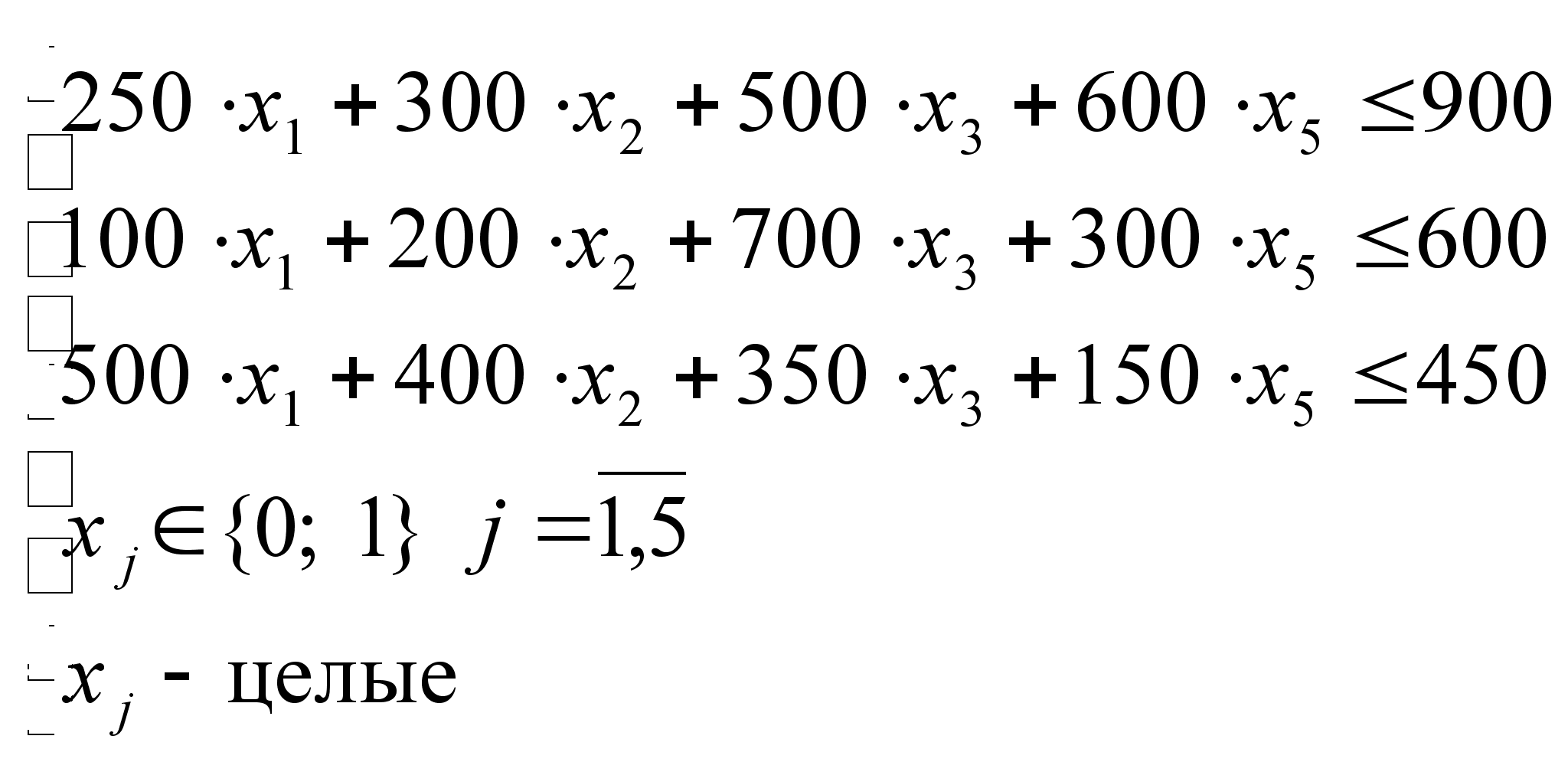 ;
;
a)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 500 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
б)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
в)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 400
миль, поэтому
![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
Таким образом,
новый опорный
план:
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
г) Вычисление верхней и нижней границ.
Вычисляем верхнюю границу:
![]() ;
– третье
ограничение
более жесткое.
;
– третье
ограничение
более жесткое.
Определяем опорные планы для третьего ограничения:
– ![]() ,
,
![]() ;
;
В
последнем
случае оставшееся
после других
городов расстояние
равно 50 миль,
поэтому ![]() .
Таким образом:
.
Таким образом:
![]() .
.
– ![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
равно 50 миль,
поэтому ![]() .
Таким образом
:
.
Таким образом
: ![]() .
.
– В этом случае
![]() .
.
Вычисляем нижнюю границу:
Т.к. ![]() ,
то
,
то ![]() ;
;
![]() ;
;
![]() .
.
8) Отсев неперспективного подмножества.
![]() .
.
Так как ![]() и
и ![]() больше Rec,
то оба подмножества
перспективные,
но поскольку
больше Rec,
то оба подмножества
перспективные,
но поскольку
![]() ,
то далее мы
будем исследовать
,
то далее мы
будем исследовать
![]() ,
как более
перспективное.
,
как более
перспективное.
![]() ;
;
![]() - здесь
- здесь
![]() .
.
![]() -
здесь
-
здесь ![]() .
.
9) Анализ множества D3.
Поскольку
![]() ,
то:
,
то:
![]()
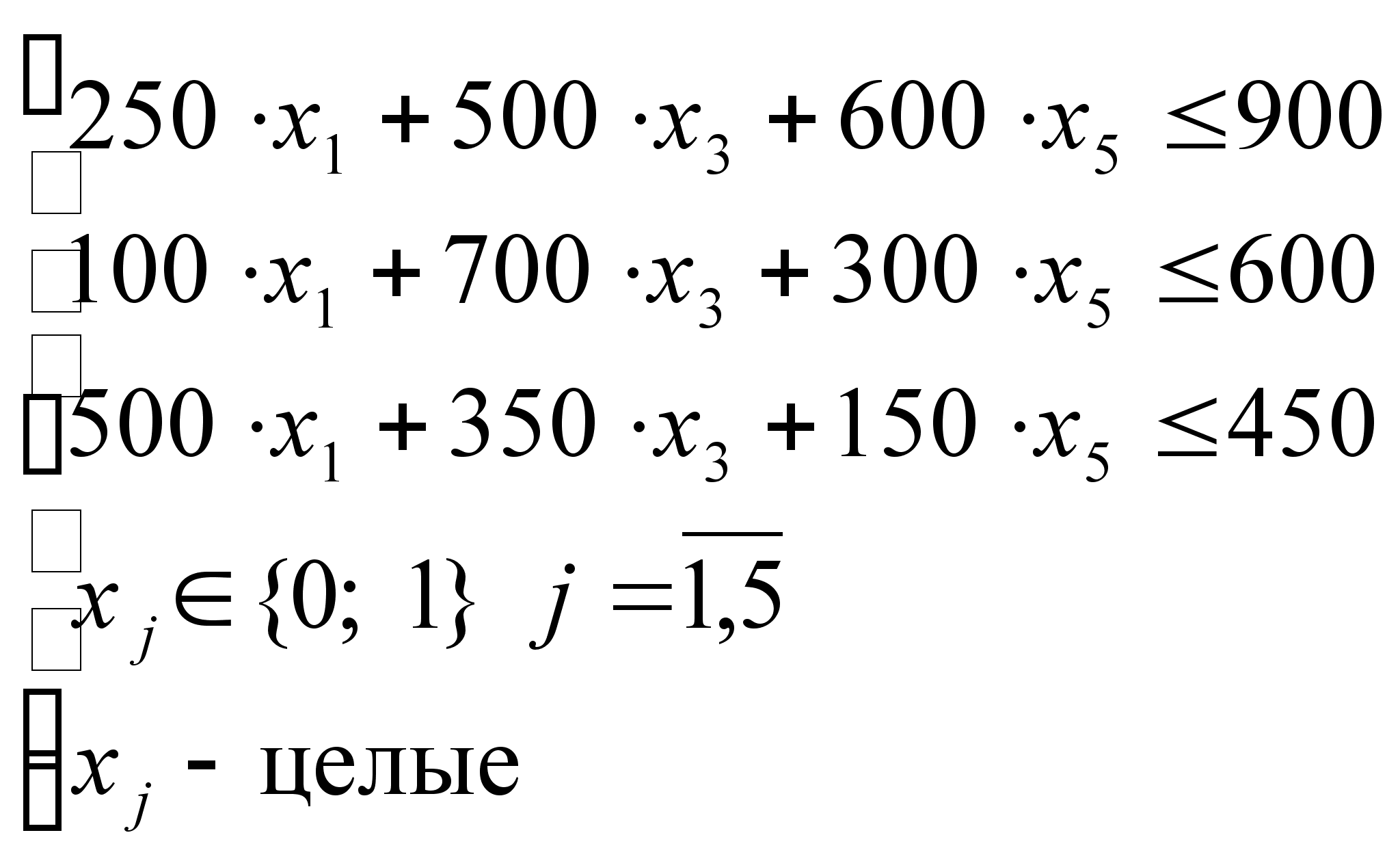
a)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 600 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
б)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 700 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
в)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 350
миль, поэтому
![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
г) Вычисление верхней и нижней границ.
Вычисляем верхнюю границу:
![]() ;
– третье
ограничение
более жесткое.
;
– третье
ограничение
более жесткое.
Определяем опорные планы для третьего ограничения:
– ![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
равно 100 миль,
поэтому ![]() .
Таким образом
:
.
Таким образом
: ![]() .
.
– ![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
равно 300
миль, поэтому
![]() .
Таким образом
:
.
Таким образом
: ![]() .
.
–
В этом случае
![]() .
.
Вычисляем нижнюю границу:
![]() ;
;
Т.к. ![]() ,
то
,
то ![]() ;
;
![]() .
.
10) Анализ множества D4.
Поскольку
![]() ,
то:
,
то:
![]() .
.
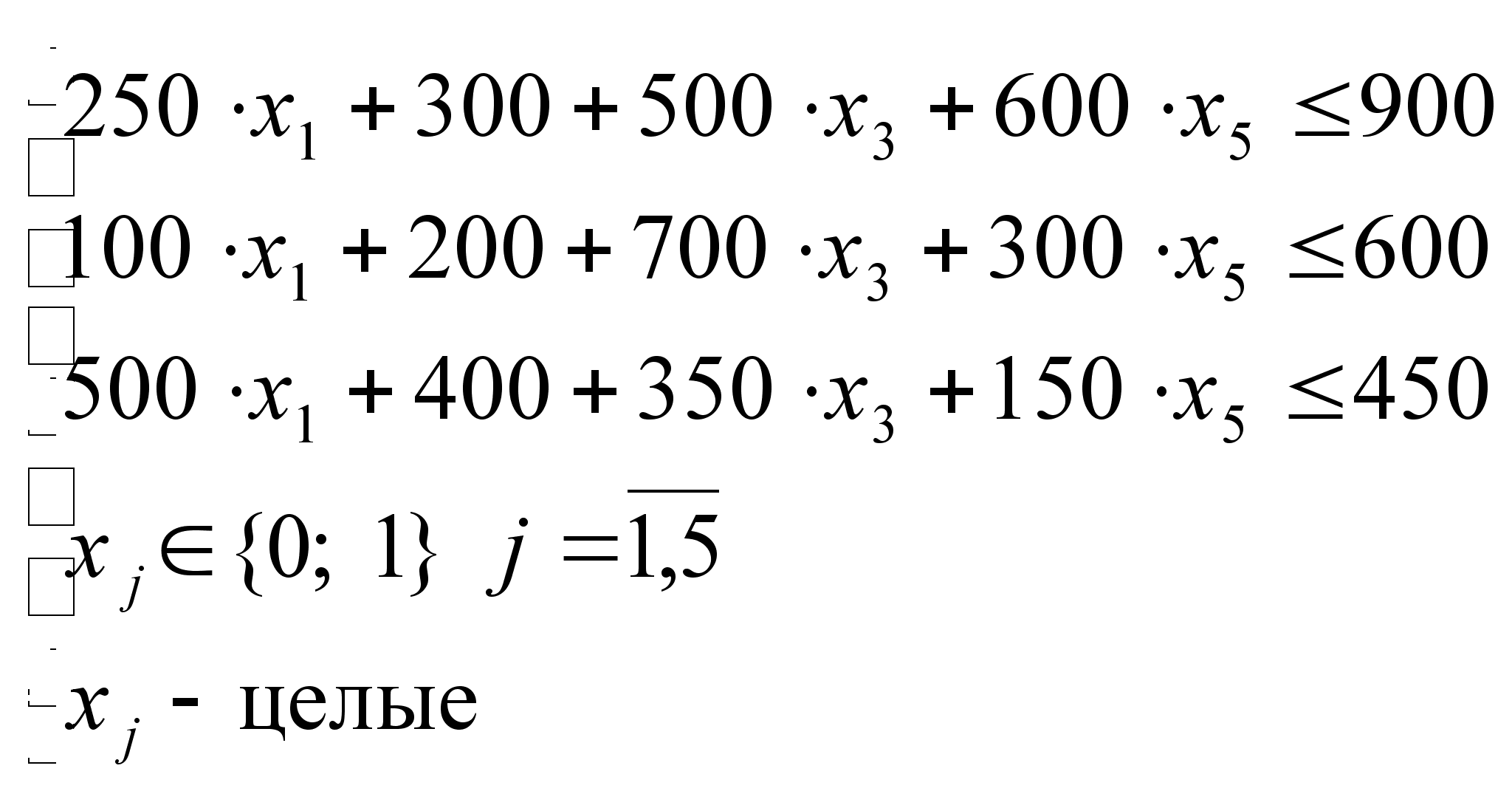 =>
=> 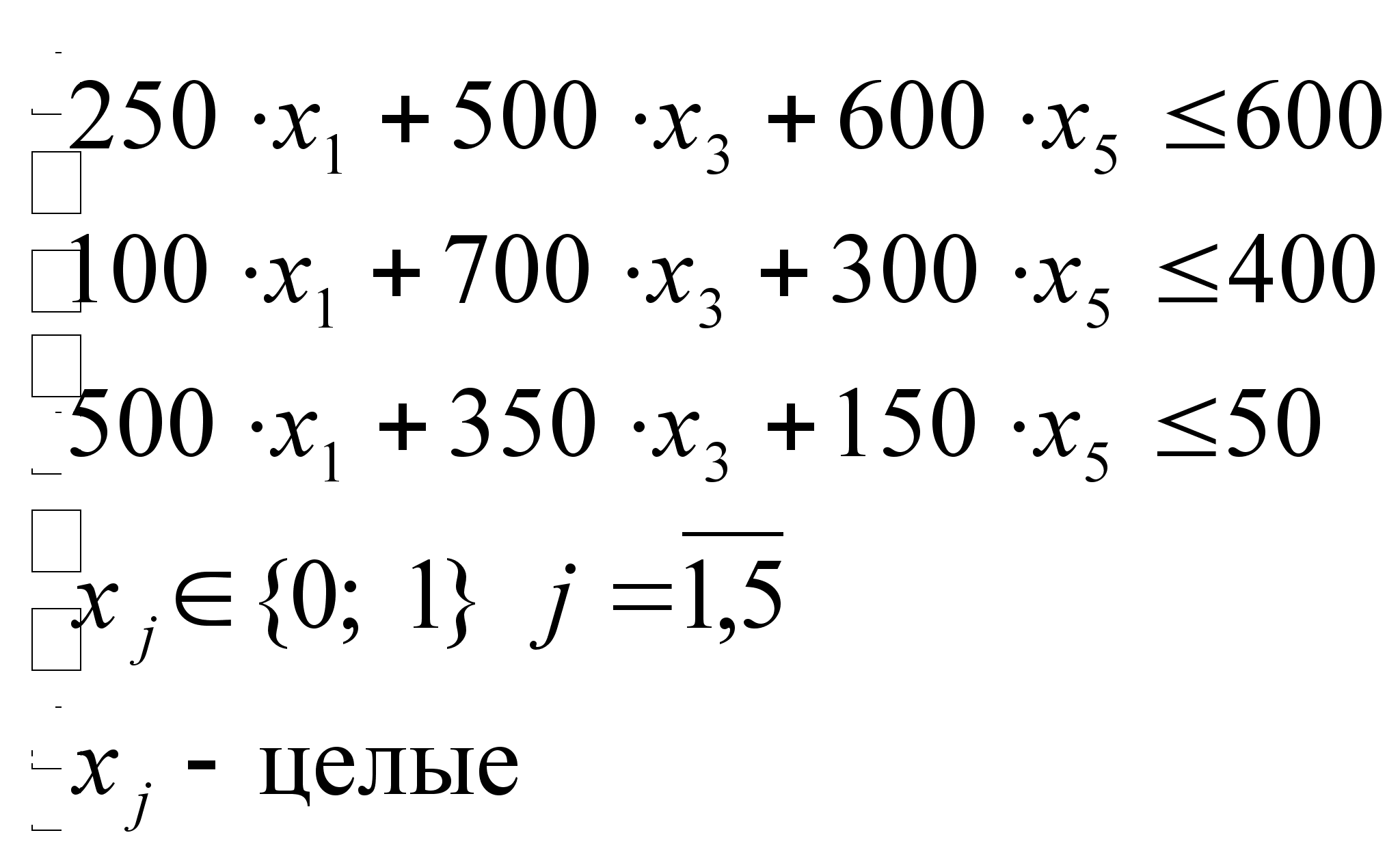 ;
;
a)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
В последнем
случае оставшееся
после других
городов расстояние
меньше 500 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
б)
Определяем
начальный план
для ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
в)
Определяем
начальный план
для ![]() :
:
В этом случае
оставшееся
после других
городов расстояние
меньше 150 миль,
поэтому ![]() будет дробным:
будет дробным:
![]() ,
=>
,
=> ![]() .
.
Таким образом,
новый опорный
план: ![]() .
.
![]() ;
;
г) Вычисление верхней и нижней границ.
Вычисляем верхнюю границу:
![]() ;
– третье
ограничение
более жесткое.
;
– третье
ограничение
более жесткое.
Определяем опорные планы для третьего ограничения:
Очевидно,
что поскольку
![]() ,
то
,
то ![]() .
.
Вычисляем нижнюю границу:
Т.к. ![]() ,
то
,
то ![]() ;
;
![]() .
.
Т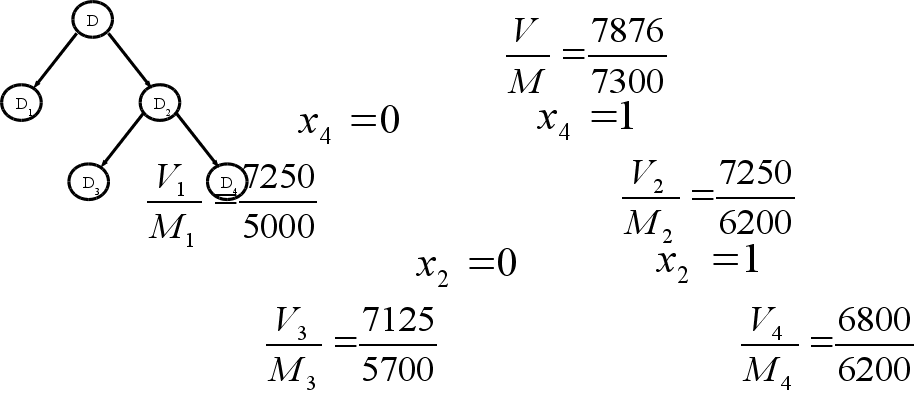 ак
как
ак
как ![]() и
и ![]() больше Rec,
то оба подмножества
перспективные,
но поскольку
больше Rec,
то оба подмножества
перспективные,
но поскольку
![]() ,
то подмножество
,
то подмножество
![]() более перспективное,
следовательно
оптимальным
планом будет
более перспективное,
следовательно
оптимальным
планом будет
![]() .
То есть города,
удовлетворяющие
всем 3 условиям
и при этом дающие
максимальную
прибыль – Детройт
и Нью-Йорк.
.
То есть города,
удовлетворяющие
всем 3 условиям
и при этом дающие
максимальную
прибыль – Детройт
и Нью-Йорк.
11
Лабораторная работа № 7
Телешовой Елизаветы, гр. 726,
Решение задачи коммивояжера методом ветвей и границ. 1. Постановка задачи.Испекла бабка колобок и поставила его остывать на окошко. И решил колобок, что пока он остывает, он вполне может обежать лес, посмотреть на лесных жителей и снова вернуться к деду и бабке. Сказано – сделано. Спрыгнул колобок из окошка и покатился в лес. Помогите колобку найти кратчайший маршрут его движения по лесу, если расстояния между норами лесных жителей, а также домом деда и бабки даны в таблице.
| Дед и бабка | Заяц | Волк | Медведь | Лиса | |
| Дед и бабка | 0 | 6 | 4 | 5 | 2 |
| Заяц | 6 | 0 | 3 | 3,5 | 4,5 |
| Волк | 4 | 3 | 0 | 5,5 | 5 |
| Медведь | 5 | 3,5 | 5,5 | 0 | 2 |
| Лиса | 2 | 4,5 | 5 | 2 | 0 |
Для решения
задачи присвоим
каждому пункту
маршрута определенный
номер: дед и
бабка – 1, заяц
– 2, волк – 3, медведь
– 4 и лиса – 5.
Соответственно
общее количество
пунктов ![]() .
Далее введем
.
Далее введем
![]() альтернативных
переменных
альтернативных
переменных
![]() ,
принимающих
значение 0, если
переход из
i-того
пункта в j-тый
не входит
в маршрут и 1 в
противном
случае. Условия
прибытия в
каждый пункт
и выхода из
каждого пункта
только по одному
разу выражаются
равенствами
(1) и (2).
,
принимающих
значение 0, если
переход из
i-того
пункта в j-тый
не входит
в маршрут и 1 в
противном
случае. Условия
прибытия в
каждый пункт
и выхода из
каждого пункта
только по одному
разу выражаются
равенствами
(1) и (2).
![]() (1)
(1)
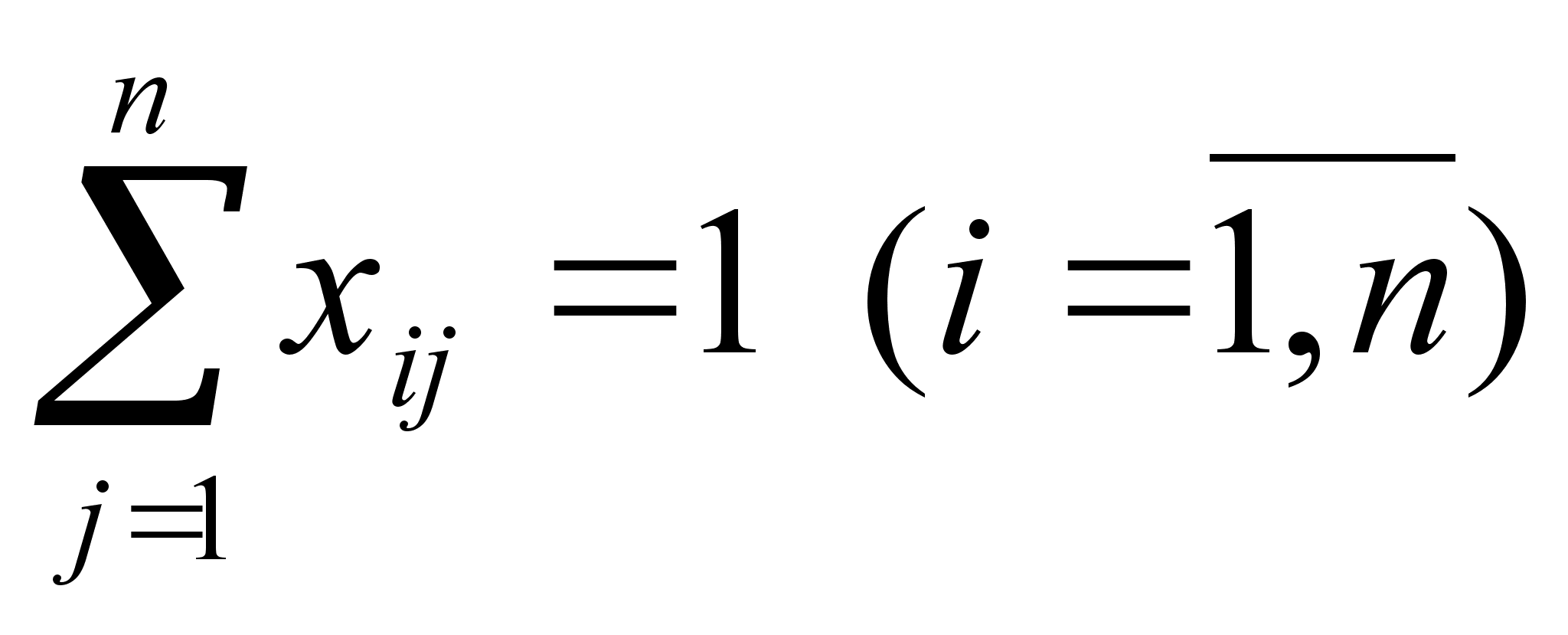 (2)
(2)
Для обеспечения
непрерывности
маршрута вводятся
дополнительно
n
переменных
![]() и
и ![]() дополнительных
ограничений
(3).
дополнительных
ограничений
(3).
![]() (3)
(3)
Суммарная протяженность маршрута F, которую необходимо минимизировать, запишется в следующем виде:
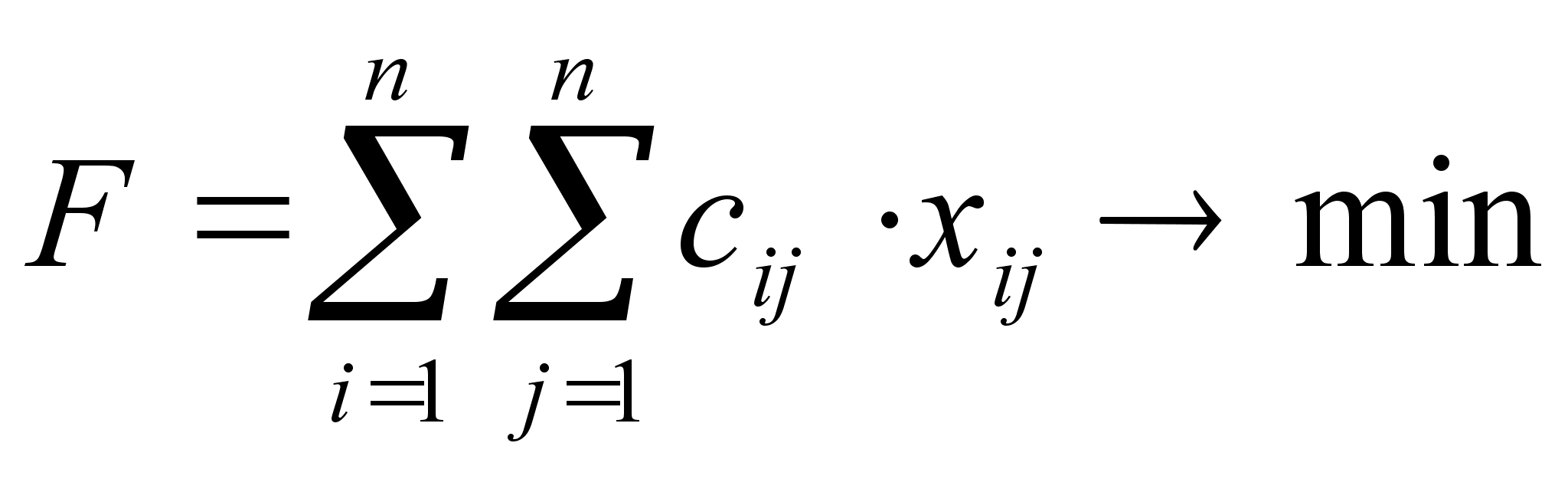 (4)
(4)
В нашем случае эти условия запишутся в следующем виде:
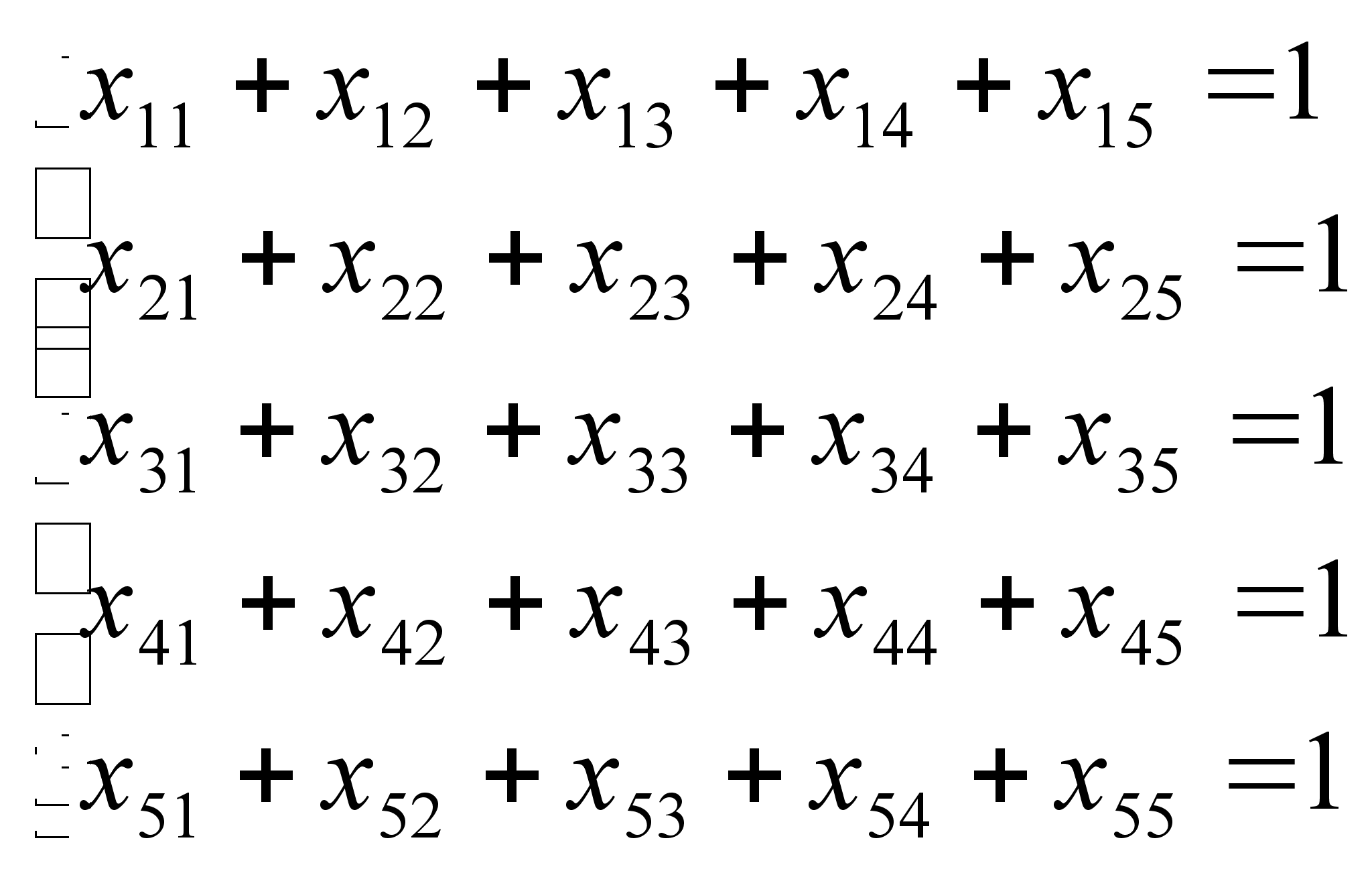 (1);
(1); 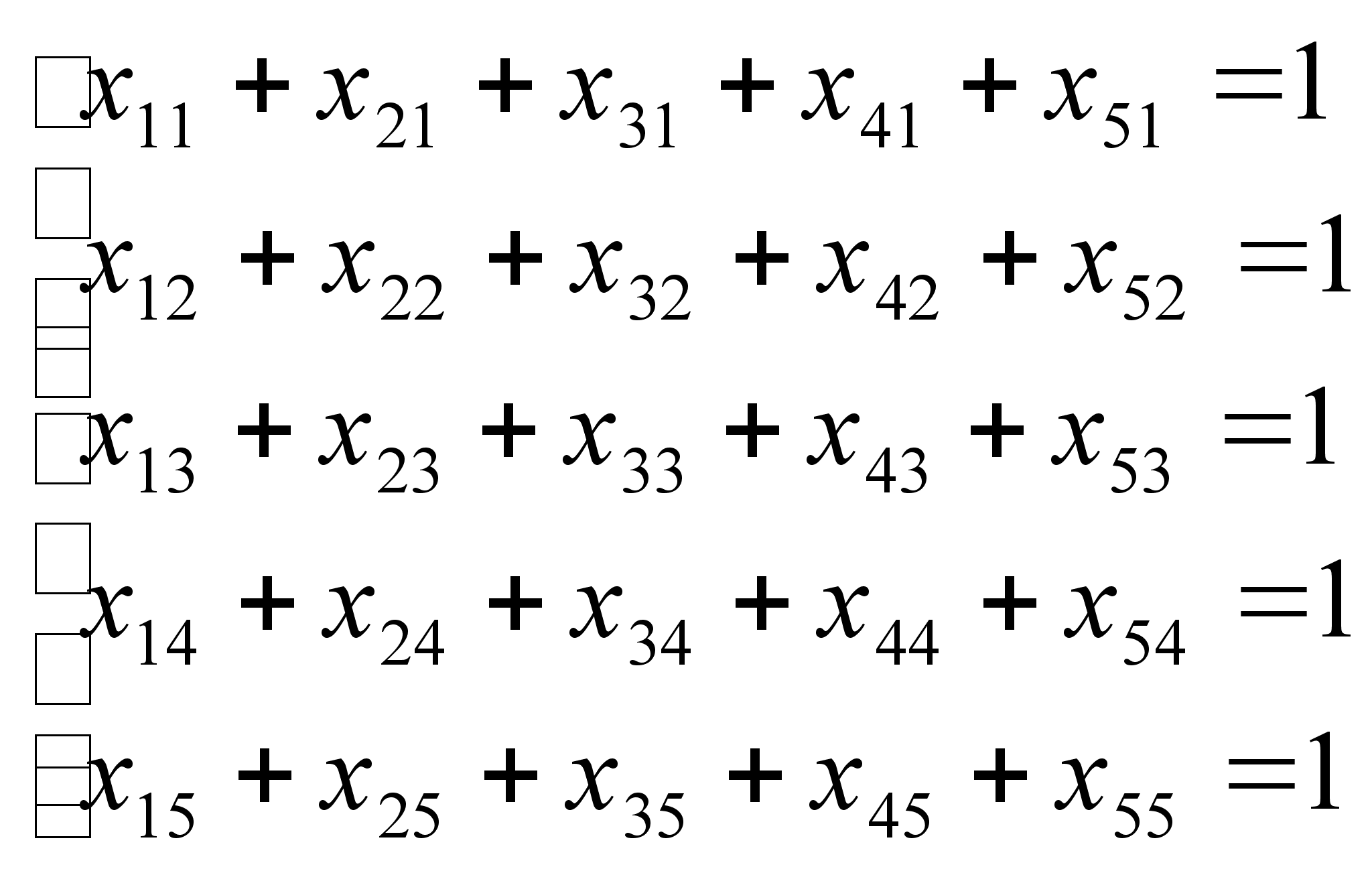 (2);
(2);
![]() (3)
(3)
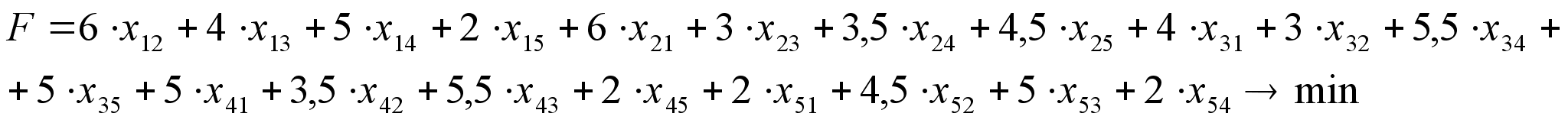 (4)
(4)
3. Решение задачи методом ветвей и границ.
1) Анализ множества D.
Найдем оценку снизу Н. Для этого определяем матрицу минимальных расстояний по строкам (1 где расстояние минимально в строке).
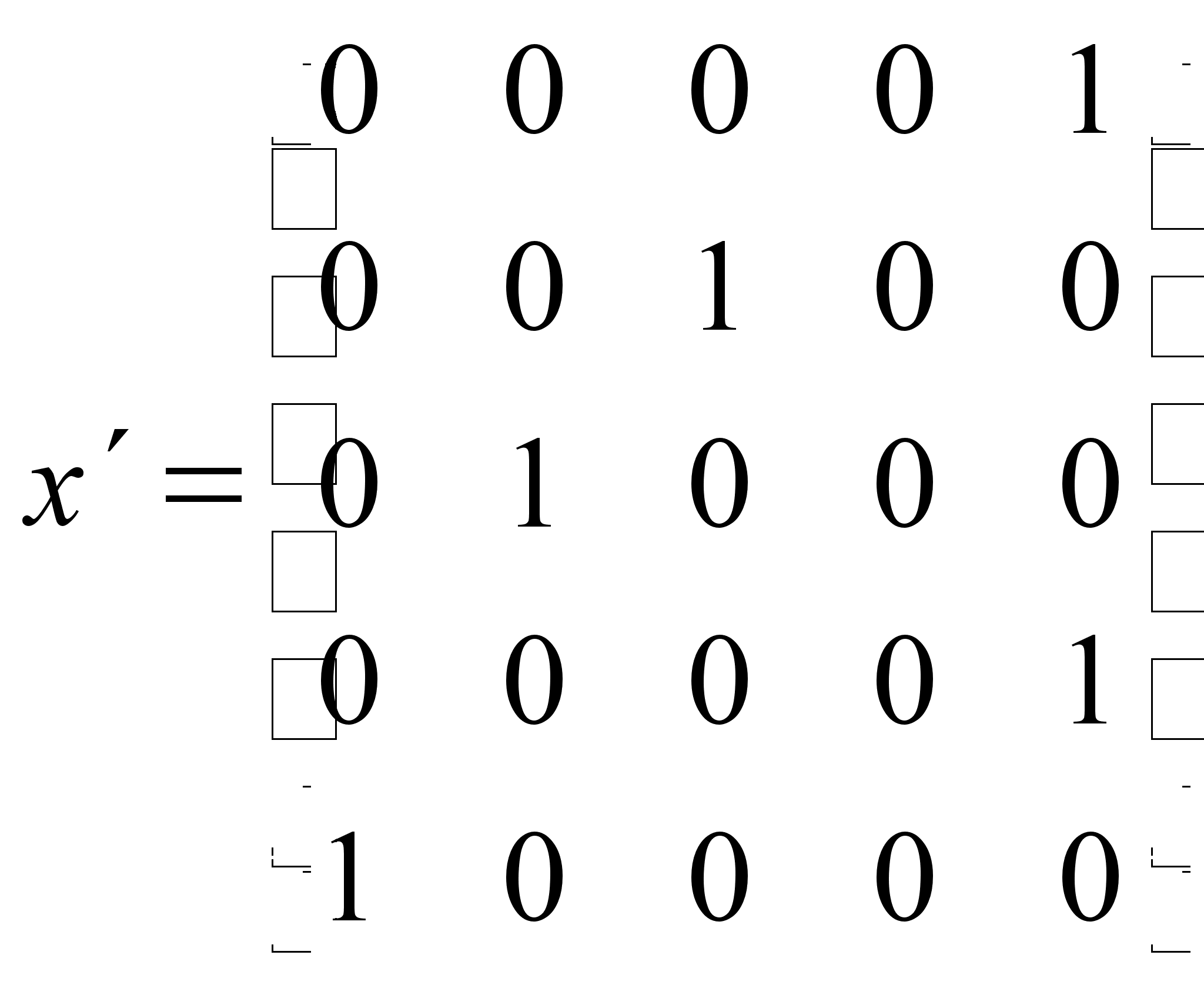 =>
=> ![]() ;
;
Аналогично определяем матрицу минимальных расстояний по столбцам.
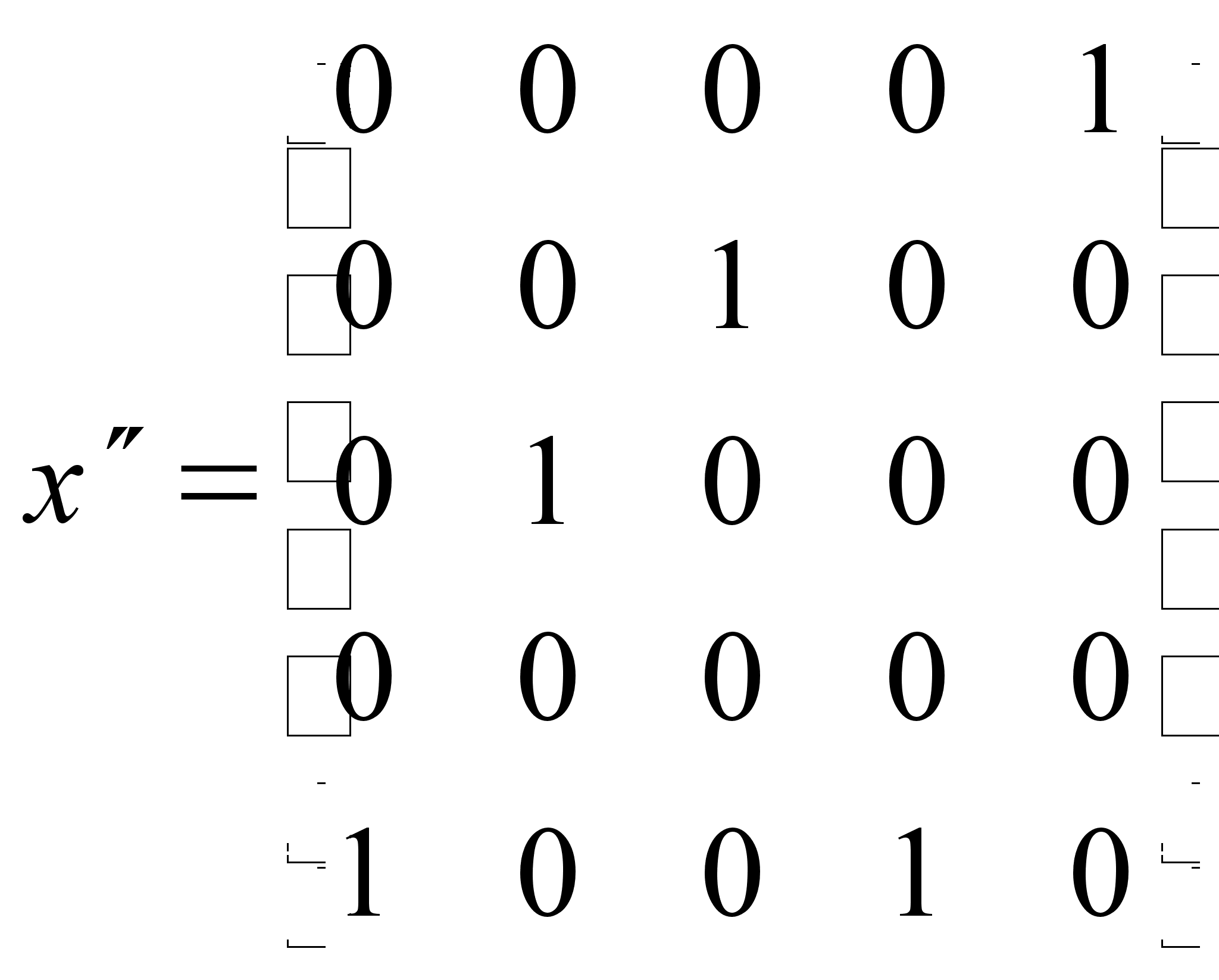 =>
=> ![]() ;
;
![]() ;
;
Выберем
начальный план:
![]() .
Тогда верхняя
оценка:
.
Тогда верхняя
оценка:
![]() .
.
Очевидно,
что ![]() ,
где
,
где ![]() означает переход
из первого
пункта в j-тый.
Рассмотрим
эти подмножества
по порядку.
означает переход
из первого
пункта в j-тый.
Рассмотрим
эти подмножества
по порядку.
2
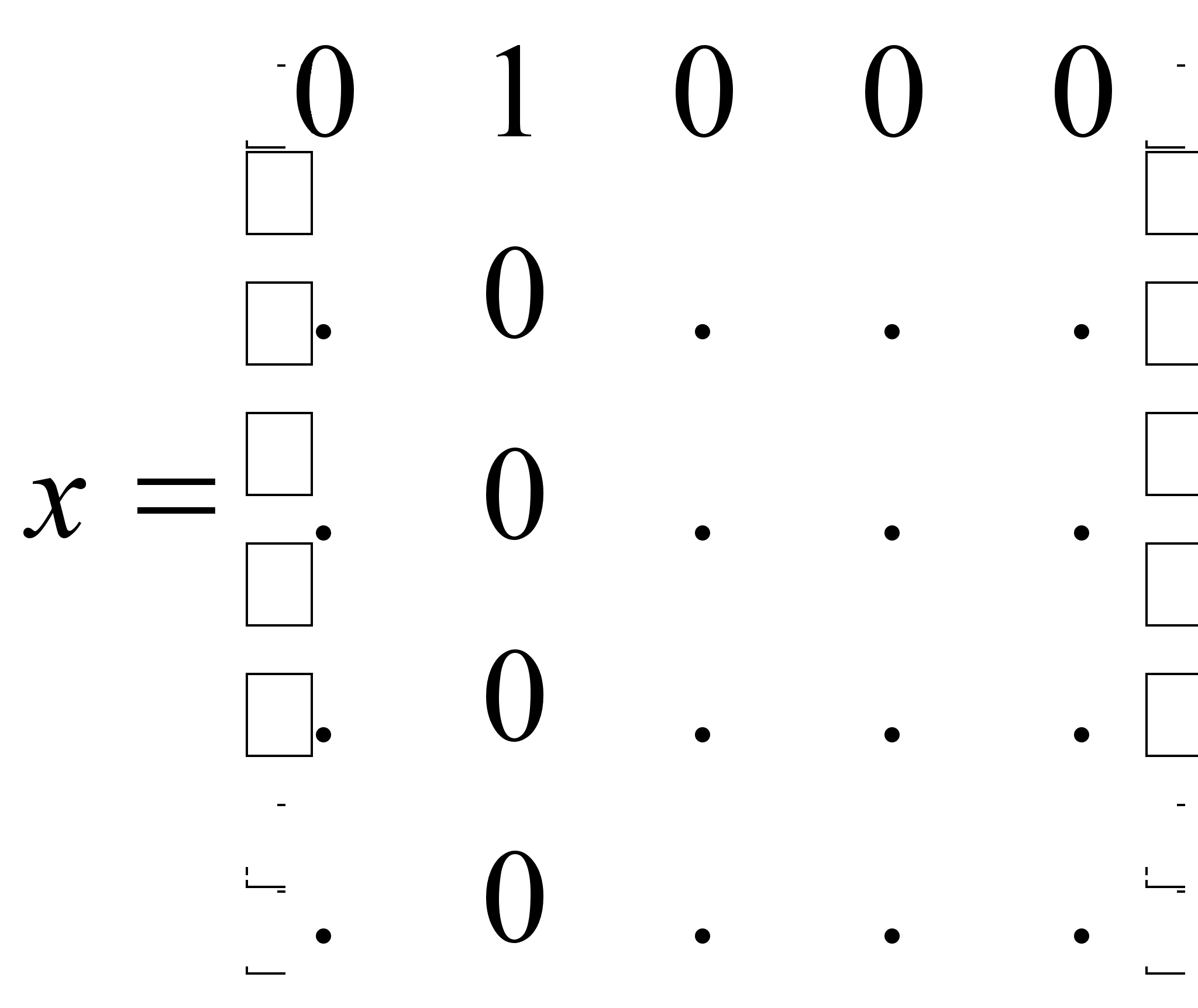
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
3
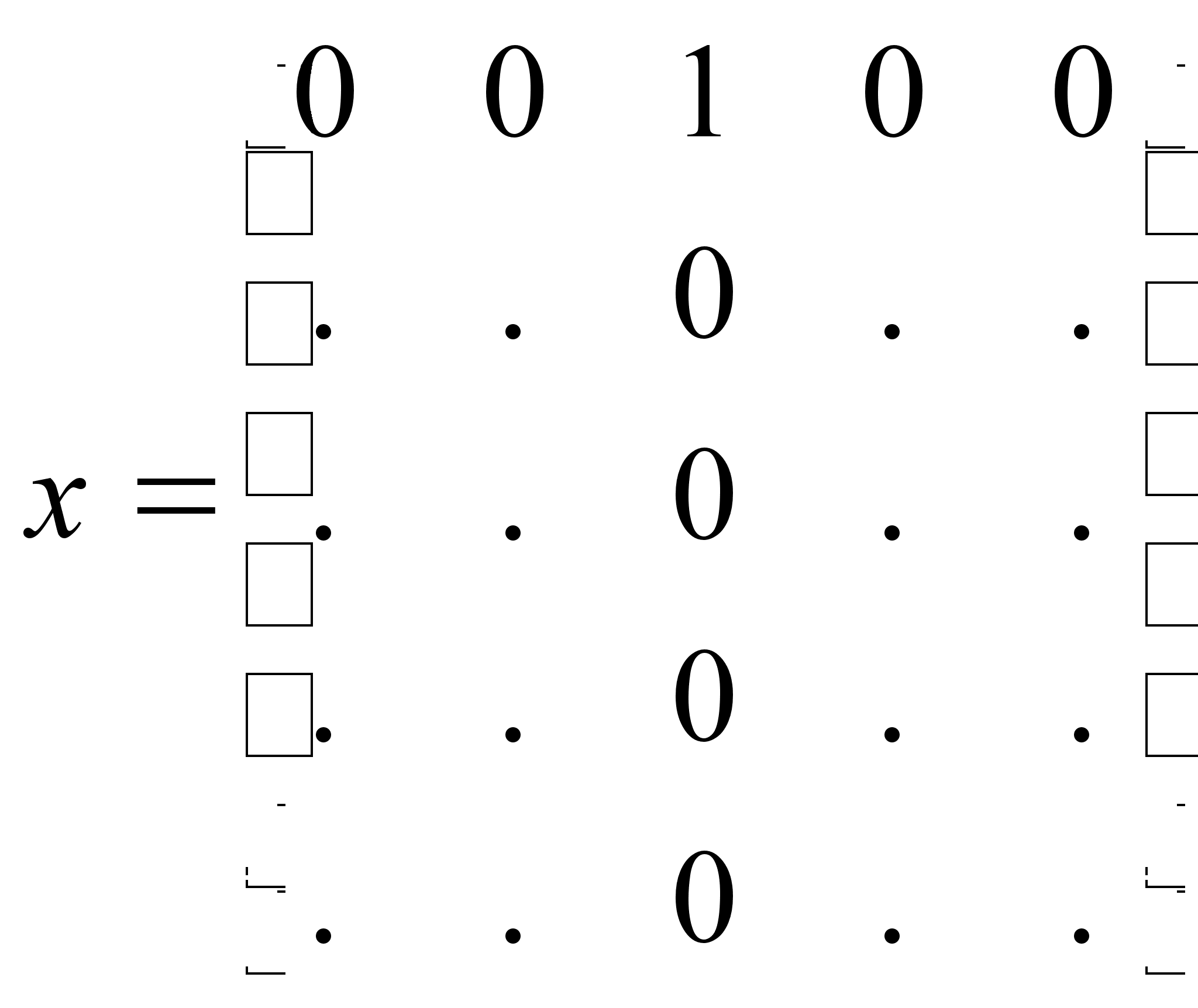
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
4
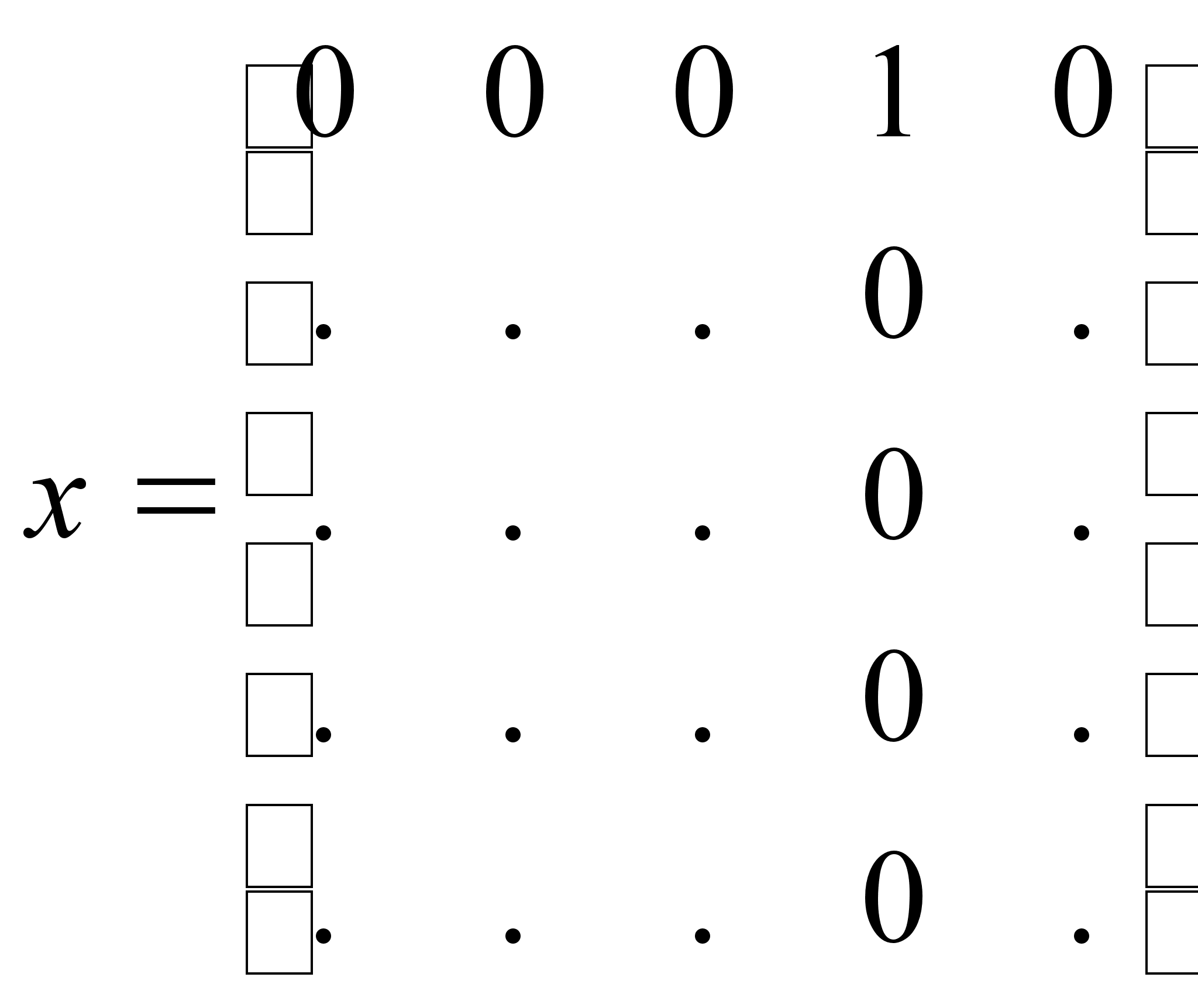
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
5
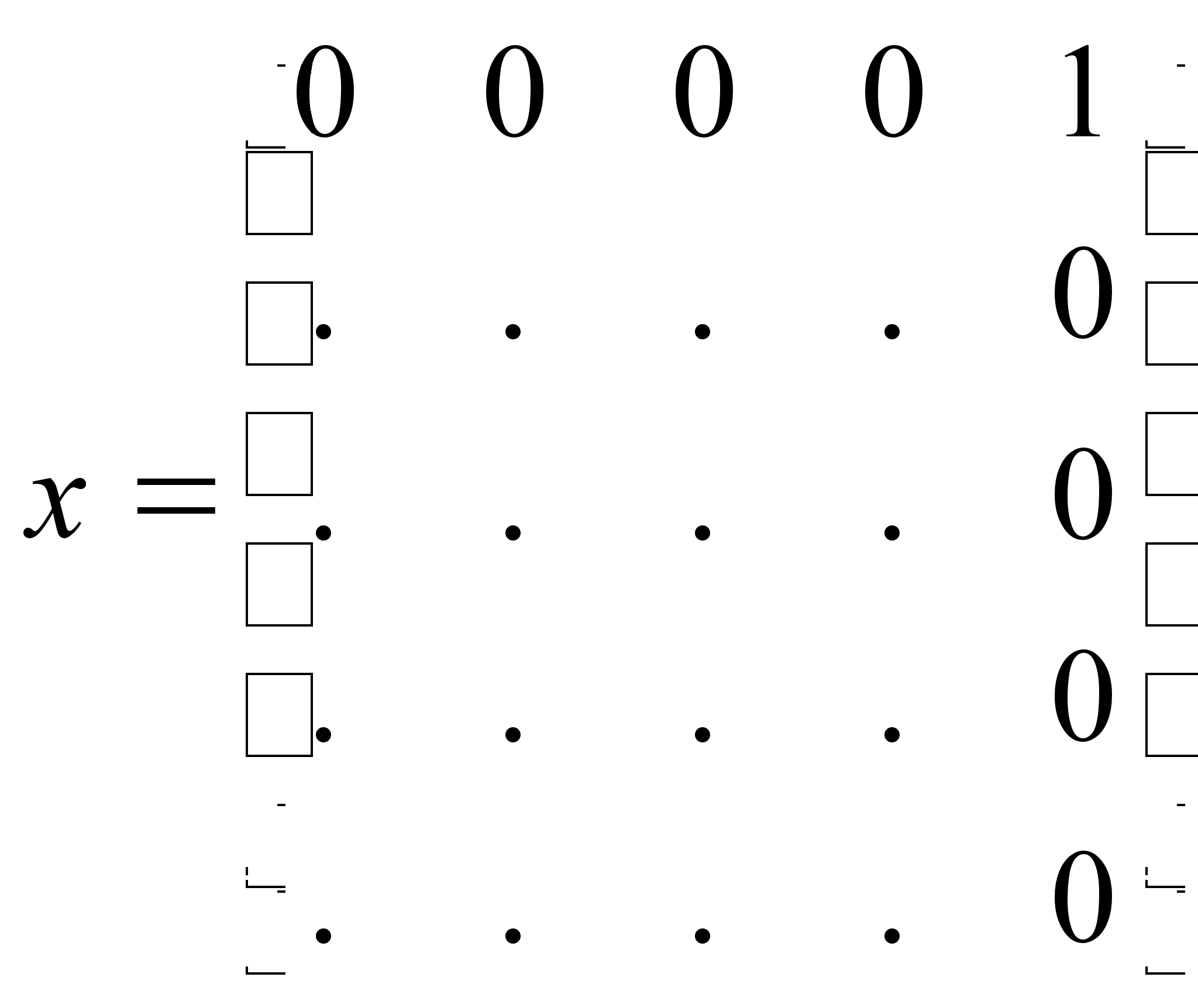
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
6) Отсев неперспективных подмножеств.
![]() ;
;
Подмножества
D13 и D15
неперспективные.
Т.к. ![]() ,
но
,
но ![]() ,
то далее будем
рассматривать
подмножество
D14.
,
то далее будем
рассматривать
подмножество
D14.
![]() .
.
7
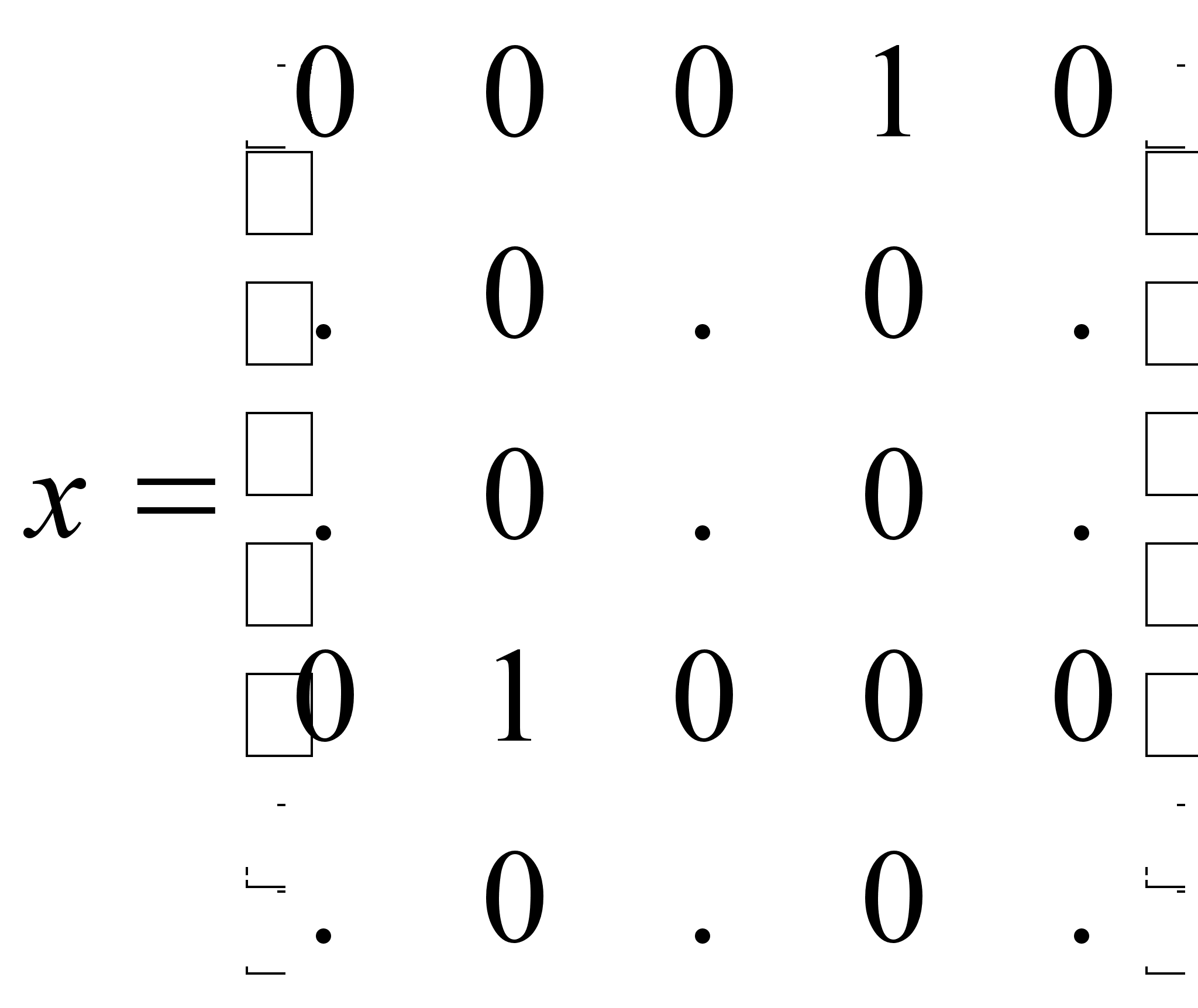
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
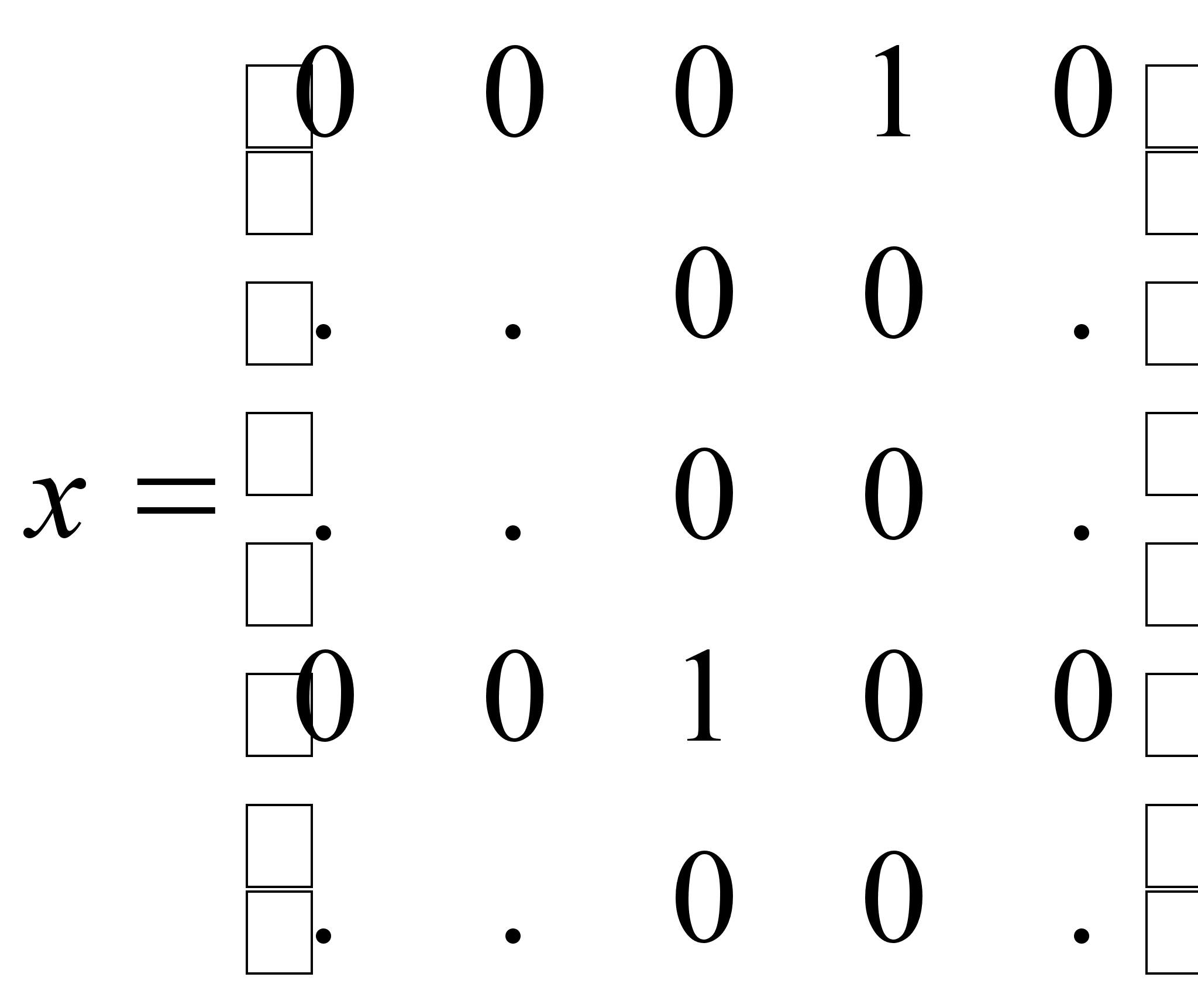
8) Анализ подмножества D143.
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]()
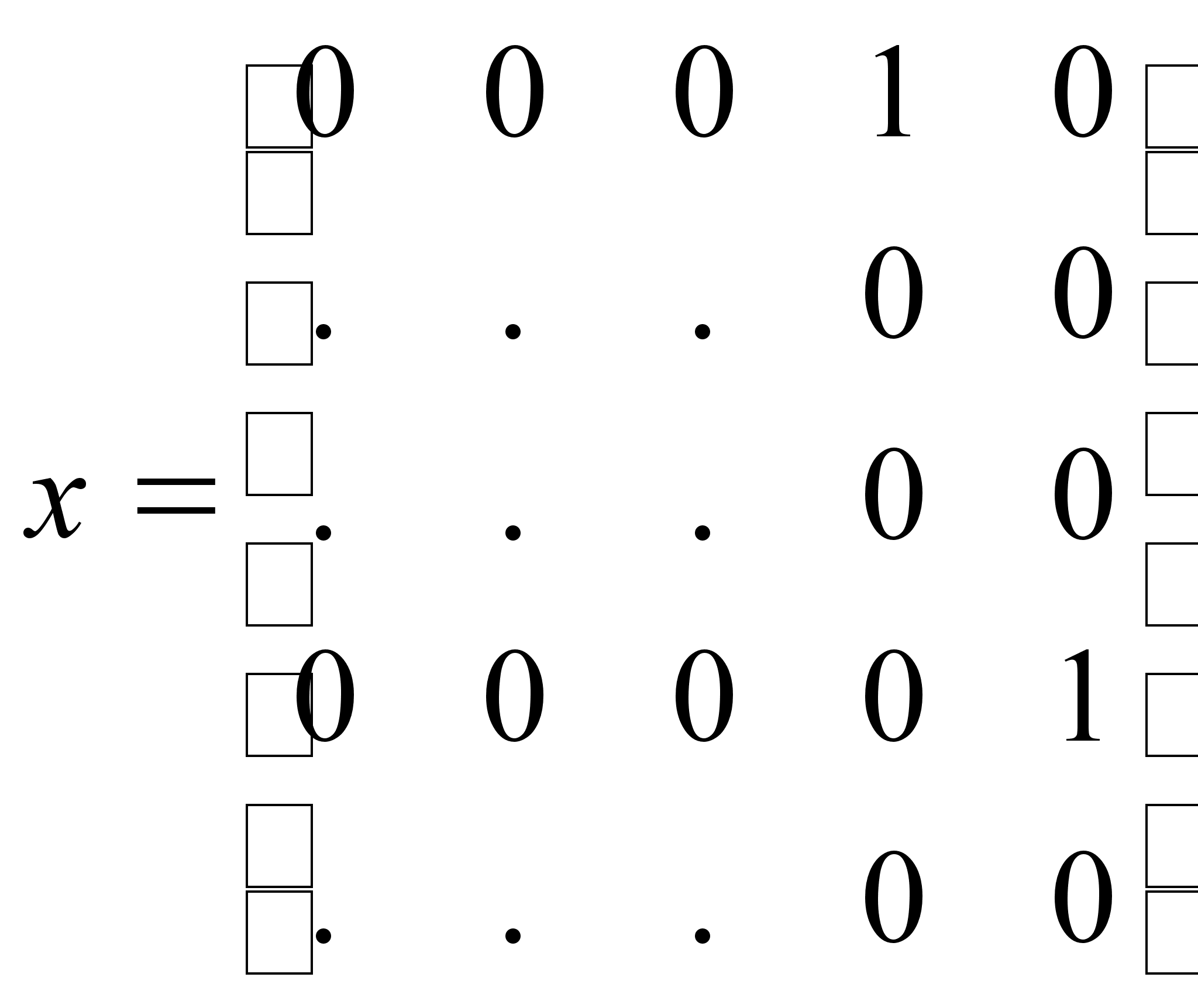
9) Анализ подмножества D145.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
10) Отсев неперспективных подмножеств.
![]() ;
;
Подмножество
D143
неперспективное.
Т.к. ![]() ,
но
,
но ![]() ,
то далее будем
рассматривать
подмножество
D145.
,
то далее будем
рассматривать
подмножество
D145.
![]() .
.
9
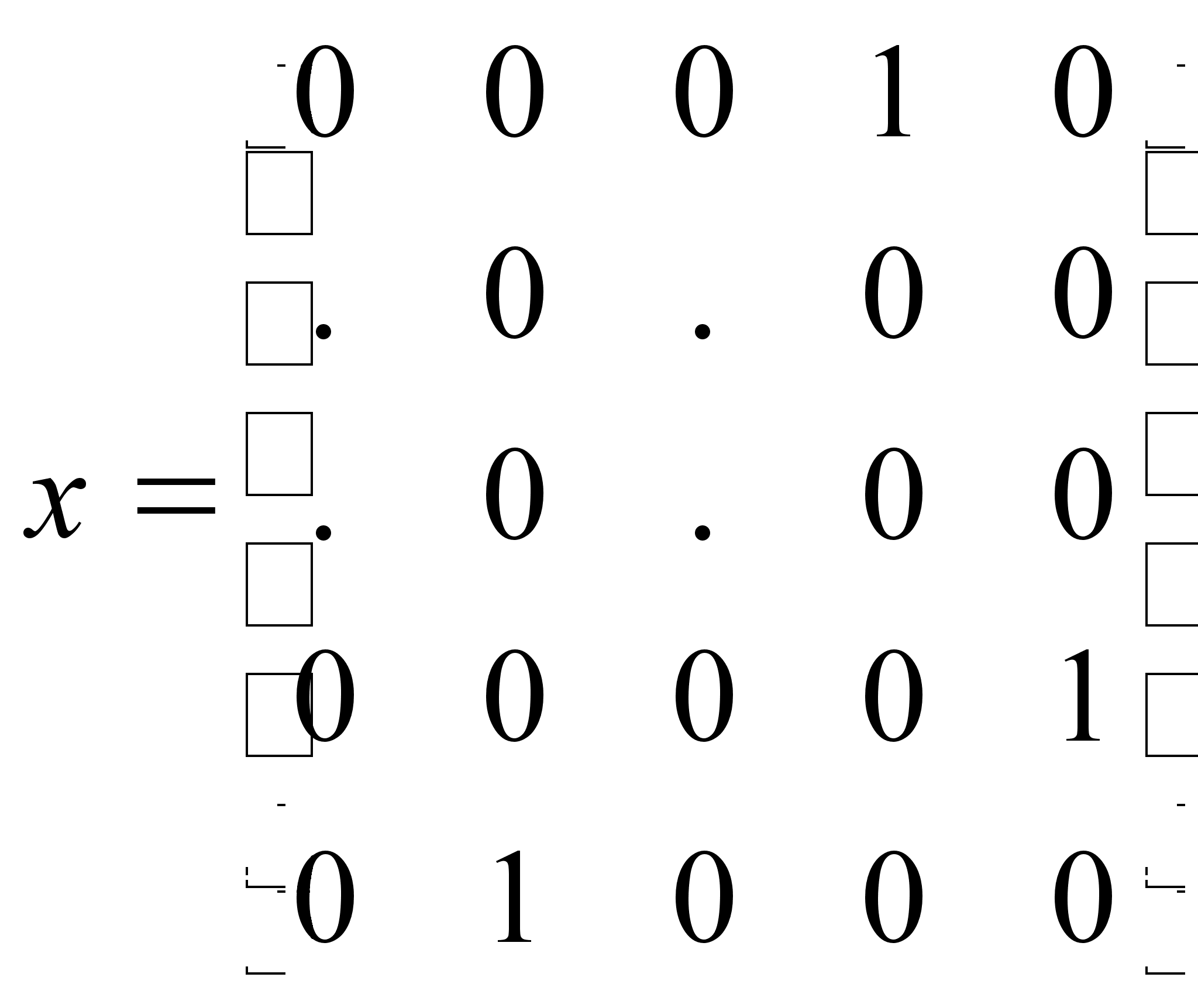
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
9
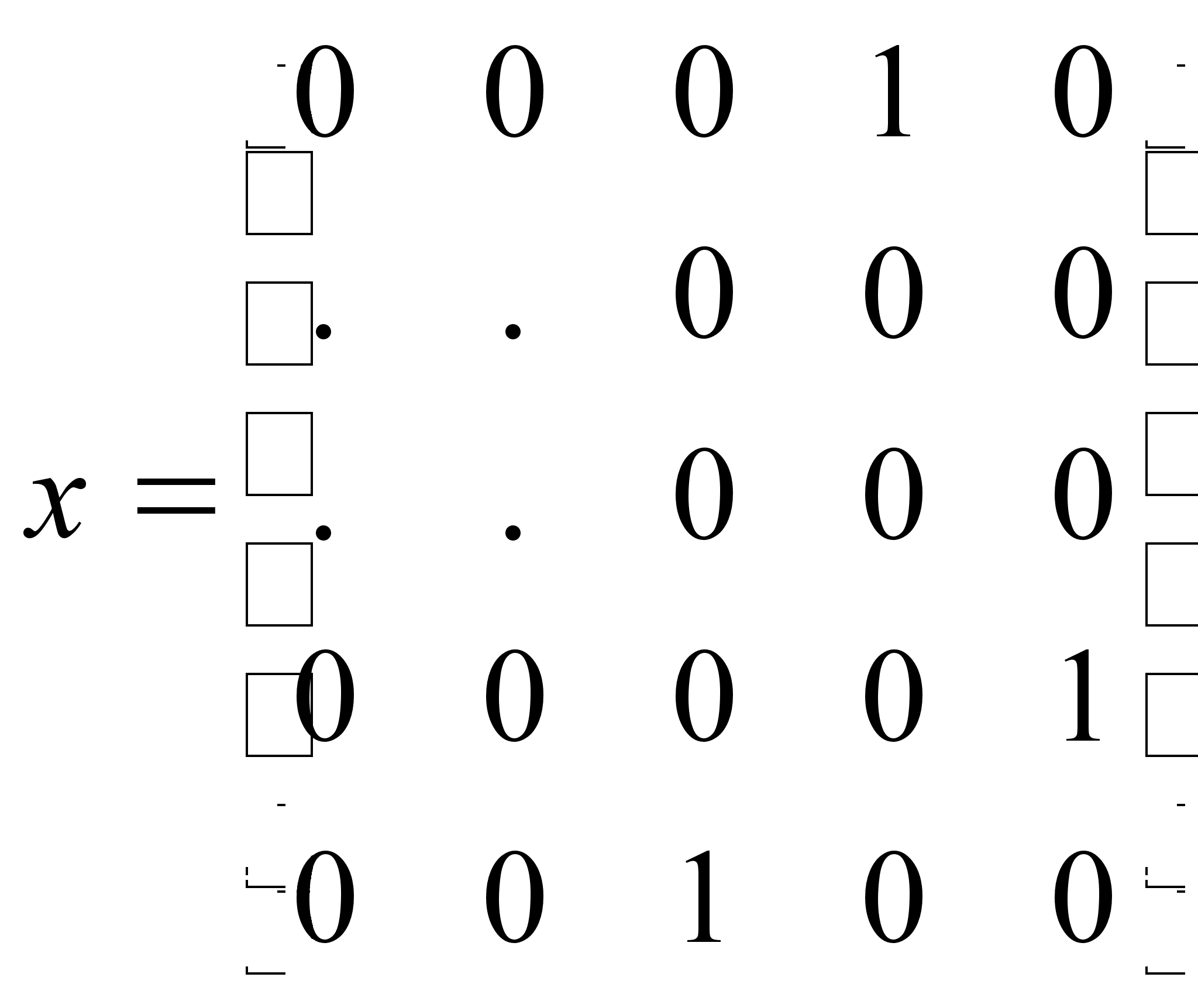
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Оптимальное
решение:
![]() .
.
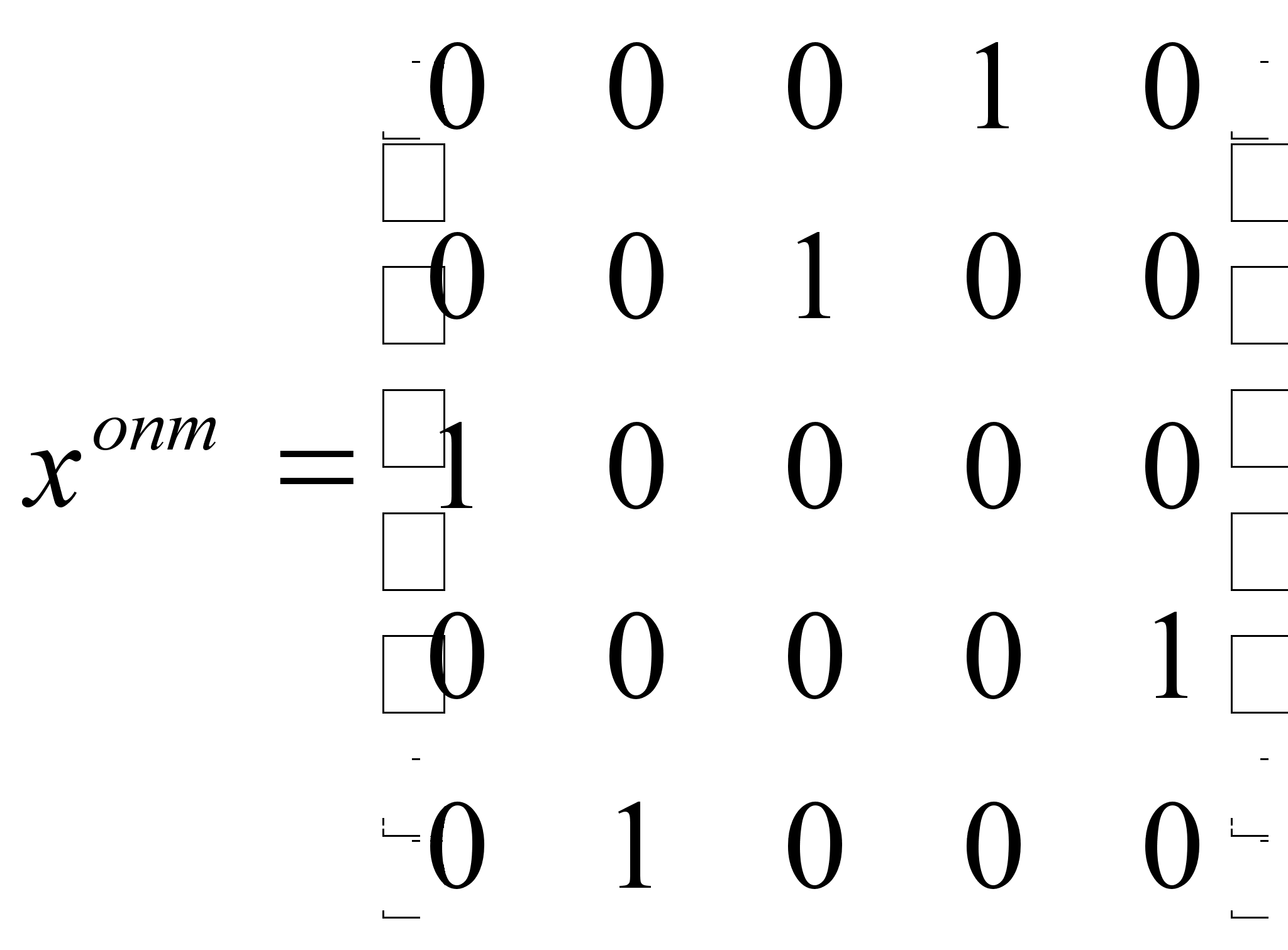 .
.
Таким образом, маршрут колобка: дед и бабка – медведь – лиса – заяц – волк – дед и бабка.
4
Похожие работы
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...
... концентрических окружностей с уменьшающимся радиусом по мере затухания колебаний скорости и момента. Аналогичная картина наблюдается при ступенчатом набросе нагрузки. 5. РАЗРАБОТКА ВИРТУАЛЬНОЙ ЛАБОРАТОРНОЙ РАБОТЫ НА БАЗЕ ВИРТУАЛЬНОЙ АСИНХРОННОЙ МАШИНЫ Иную возможность анализа АД представляет специализированный раздел по электротехнике Toolbox Power System Block. В его библиотеке имеются блоки ...
... Р- 122”.- Техническое описание. 3 “Техника чтения схем автоматического управления и технологического контроля”. – Энергоатомиздат, 1991.4 ДОКЛАД “Проект лабораторного стенда по изучению частотного электропривода на базе автономного инвертора напряжения фирмы OMRON”. В настоящее время на АО “Северсталь” происходит активное внедрение частотных преобразователей. Это объясняется тем, что частотное ...
0 комментариев