Навигация
Приближенное нахождение квазирешений
2.3. Приближенное нахождение квазирешений
В предыдущем параграфе мы видели, что нахождение квазирешения связано с нахождением элемента в бесконечномерном пространстве. Для приближенного нахождения квазирешения естественно переходить к конечномерному пространству. Можно указать достаточно общий подход к приближенному нахождению квазирешений уравнения (2; 0,1) , в котором А—вполне непрерывный оператор.
Будем полагать, что выполнены указанные в 2.2. достаточные условия существования единственного квазирешения на заданном множестве М, т. е. полагаем, что множество М — выпуклый компакт и сфера в пространстве U строго выпукла. Пусть
M1 Ì M2 Ì...Ì Mn Ì...
— возрастающая цепочка компактных замкнутых множеств Мn такая, что замыкание их объединения ![]() совпадает с М. Квазирешение уравнения (2; 0,1) существует на каждом множестве Мn . Но оно может быть не единственным. Обозначим через Тn совокупность всех квазирешений на множестве Мn .
совпадает с М. Квазирешение уравнения (2; 0,1) существует на каждом множестве Мn . Но оно может быть не единственным. Обозначим через Тn совокупность всех квазирешений на множестве Мn .
Покажем, что в качестве приближения к квазирешению z1 на множестве М можно брать любой элемент z1n из Тn . При этом
![]()
Пусть Nn = АМn и Вn — множество проекций элемента и на множество Nn . Очевидно, что Вn = АТn и N1 Í N2 Í …Í Nn; тогда
r U(u,N1)>= …>=r U (u,Nn)>=… r U (u,N)= r U (u,Az1) . (2;3,1)
Так как множество ![]() всюду плотно на N, то для всякого e >0 найдется такое число n0(e), что для всех п >n0(e)
всюду плотно на N, то для всякого e >0 найдется такое число n0(e), что для всех п >n0(e)
rU(u,Nn)< rU(u,N)+ e (2; 3,2)
Из (2; 3,1) и (2; 3,2) следует, что
![]() (2;3,3)
(2;3,3)
| Поскольку то |
|
|
|
|
(2;3,4)
Каждое множество Вn есть компакт, так как оно является замкнутым подмножеством компакта Nn. Поэтому в Вn найдется такой элемент уn , что
rU(yn ,u) = inf rU(y,u)
yÎBn
Последовательность {yn} имеет хотя бы одну предельную точку, принадлежащую N, так как N — компакт. Пусть у0 — какая-нибудь предельная точка множества {yn} и {уnk} — подпоследовательность, сходящаяся к y0 , т. е.
![]()
Из (2; 3,3) и (2; 3,4) следует, что
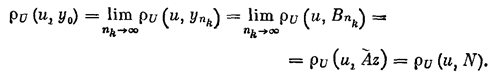
Таким образом,
rU(u,y0)= rU(u,N).
Отсюда и из единственности квазирешения на множестве М следует, что
y0=Az1.
Так как у0 — произвольная предельная точка множества {yn}, то последовательность {уn} сходится к Аz1. Это и означает, что в качестве приближения к квазирешению можно брать любой элемент z1n из множества Тп, так как в силу леммы параграфа 2.1. z1nàz* при nà¥.
Если в качестве Мп брать конечномерные (n-мерные) множества, то задача нахождения приближенного квазирешения на компакте М сводится к минимизации функционала rU(Az, u) на множестве Мп , т. е. к нахождению минимума функции п переменных.
2.4. Замена уравнения Аz=u близким ему
Уравнения вида (2; 0,1), в которых правая часть u не принадлежит множеству N=AM, изучались М. М. Лаврентьевым . Ему принадлежит идея замены исходного уравнения (2; 0,1) близким ему, в некотором смысле, уравнением, для которого задача нахождения решения устойчива к малым изменениям правой части и разрешима для любой правой части u ÎU. В простейшем случае это делается следующим образом.
Пусть F ºU ºН — гильбертовы пространства, А — линейный, ограниченный, положительный и самосопряженный оператор, SR º {х, ||x||<=R, xÎF} есть шар радиуса R в пространстве F, В — вполне непрерывный оператор, определенный на SR при любом R > 0. В качестве класса корректности М берется множество DR=BSR — образ шара SR при отображении с помощью оператора В. Предполагается, что искомое точное решение zT уравнения (2; 0,1) с правой частью u=uT существует и принадлежит множеству DR. Уравнение (2; 0,1) заменяется уравнением
(A+aE)z º Az+az=u , (2:4,1)
где a>0 – числовой параметр. Решение уравнения
za=(A+aE)-1u , (2; 4,2)
при соответствующем выборе параметра a, принимается за приближенное решение уравнения (2; 0,1). Здесь Е — единичный оператор.
Замечание. Для оценки уклонения rF(zT,zd) приближенного решения от точного можно использовать модуль непрерывности w обратного оператора на N.
Пусть u1, u2 Î N и rU(u1,u2)<=d. Тогда
w(d,N)= sup rF(A-1u1,A-1u2).
u1,u2 ÎN
Очевидно, что если rU(uT,ud)<= d и zd=A-1ud , то
rF(zT,zd)<=w(d,N).
Вернемся к уравнению (2; 4,1). Если || Az ||<=d и w(d,DR) = sup || z ||, то легко
DR
получить оценку уклонения za от zT. Очевидно, что
|| za- zT ||<=||za1 - zT|| + ||za- za1||, (2;4,3)
где
za1=(A + aE)-1uT.
Следовательно,
||za - zT||<=w(d,DR) + d/a. (2;4,4)
Если известен модуль непрерывности w(d,DR) или его мажоранта, то из (2; 4,4) можно найти значение параметра w как функцию d, при котором правая часть в неравенстве (2; 4,4) будет минимальной.
2. 5. Метод квазиобращения
2.5.1. Известно, что задача Коши для уравнения теплопроводности с обратным течением времени является неустойчивой к малым изменениям начальных значений. Неустойчивость сохраняется и в случаях, когда решение подчиняется некоторым дополнительным граничным условиям. Для устойчивого решения таких задач разработан метод квазиобращения . Мы изложим существо его для простейшего уравнения теплопроводности, не вдаваясь в вопросы обоснования. Подробное изложение в применении к более широкому классу задач содержится в .
2.5.2. Рассмотрим прямую задачу. Пусть D — конечная область n-мерного евклидова пространства Rn точек x = (x1, x2, ..., xn), ограниченная кусочно-гладкой поверхностью S, a t — время. Пусть, далее, j(x) — заданная непрерывная в D функция. Прямая задача состоит в нахождении решения u=u(x,t) уравнения
![]() (2;5,1)
(2;5,1)
в области G º {x Î D, t > 0}, удовлетворяющего граничным условиям
u(х, t) =0 при xÎS (2; 5,2)
и начальным условиям
u(x, 0)= j(x). (2; 5,3)
Здесь
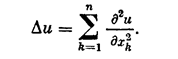
Известно, что решение такой задачи существует. Каждой функции j(x)ÎC отвечает решение задачи (2; 5,1)— (2; 5,3). Будем обозначать его через u(х, t; j).
Обратная задача состоит в нахождении функции j(х) по известной функции u(х,t; j). В реальных задачах функция u(x,t;j) обычно получается в результате измерений и, следовательно, известна приближенно. Будем полагать, что uÎL2. Такая функция может и не соответствовать никакой «начальной» функции j(х). Таким образом, может не существовать в классе функций С решения обратной задачи. Поэтому будем рассматривать задачу нахождения некоторого обобщенного решения обратной задачи.
Пусть заданы число T > 0 и функция y(x), определенная в области D, y(x) ÎL2. На функциях j(х) класса С определен функционал
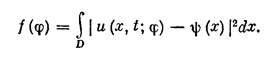
Обобщенным решением обратной задачи будем называть функцию j(х)., на которой достигается
f0=inf f(j)
jÎC
Замечание. «Естественный» подход к решению этой задачи — выбрать функцию j(х).так, чтобы f(j)=0 .
Для этого достаточно найти решение прямой задачи
![]()
u(x, t) = 0 для х Î S, 0 < t < T;
u(x,T) = y(x)
и положить j (x) = u(x,0). Но такая задача при заданной функции y(x) из L2, вообще говоря, неразрешима и, кроме того, неустойчива к малым изменениям функции y(x).
На некотором классе обобщенных функций j (x) f0=0 . Поэтому рассматривается задача нахождения приближенного значения f0 с заданным уровнем погрешности.
Для заданного числа e > 0 найти функцию je(x), на которой f (je)<=e.
Эта задача и решается методом квазиобращения.
Идея метода квазиобращения состоит в том, что вместо оператора теплопроводности ![]() находится «близкий» ему оператор Вa, для которого задача с обращением отсчета времени
находится «близкий» ему оператор Вa, для которого задача с обращением отсчета времени
Baua = 0, x Î D, t < Т, a > 0;
ua(x,T)= y(x);
ua(x,t) = 0 для xÎ S, t< Т
устойчива. Решив эту задачу, полагают j (x)=ua(x,0). Обычно в качестве оператора Вa берут оператор ![]() и решают прямую задачу
и решают прямую задачу
xÎ D, t<T, a>0;
|
|
ua(x,T)= y(x);
ua(x,t) = 0 для xÎ S, 0< t<= Т
Dua=0 для xÎ S, 0< t<= Т.
Затем полагают
j (x)=ua(x,0).
Следует отметить, что uaне сходится в обычном смысле при a à0.
3.МЕТОД РЕГУЛЯРИЗАЦИИ РЕШЕНИЯ ОПЕРАТОРНЫХ УРАВНЕНИЙ
В главе предыдущем разделе рассмотрены случаи, когда класс возможных решений уравнения (2; 0,1) является компактом. Однако для ряда прикладных задач характерна ситуация, когда этот класс F не является компактом, и, кроме того, изменения правой части уравнения
Аz= u, (3; 0,1)
связанные с ее приближенным характером, могут выводить за пределы множества AF — образа множества F при отображении его с помощью оператора А. Такие задачи называются существенно некорректными. Был разработан новый подход к решению некорректно поставленных задач, позволяющий строить приближенные решения уравнения (3; 0,1), устойчивые к малым изменениям исходных данных, для существенно некорректных задач. В основе этого подхода лежит фундаментальное понятие регуляризирующего оператора (P.O.) . Для упрощения изложения в настоящей главе мы будем полагать, что в уравнении (3; 0,1) приближенной может быть лишь правая часть и, а оператор А известен точно.
Похожие работы
... , действующий из нормированного пространства Z в нормированное пространство U. В 1963 г. А.Н.Тихонов дал знаменитое определение регуляризирующего алгоритма (РА), которое лежит в основе современной теории некорректно поставленных задач. Определение. Регуляризирующим алгоритмом (регуляризирующим оператором) называется оператор, обладающий двумя следующими свойствами: 1) определен для любых δ ...
... при решении предусмотренных задач одна из эталонных схем (рабочая) копируется в рабочие файлы. Для моделирования, анализа и хранения режимов создана база режимов (до 12 режимов). Предусмотрена возможность записи произвольного режима, являющегося результатом решения одной из задач, в базу режимов. Все расчеты, включая и формирование отображаемых на дисплеях кадров, производятся на ЭВМ ИВП. В ИВП ...
... из-за дефектов производства, технологии изготовления, загрязнения поверхности, погрешности измерения и обработки экспериментальной информации. Влияние погрешностей исходной информации на решение обратной задачи теплопроводности оценивалось с помощью метода статистических испытаний Монте – Карло / 5-8 /. Анализ результата статистического моделирования решения обратной задачи позволяет установить ...
... и получим . ЧТД. Пример. Вычислим значение , где . Действие Содержимое НГ ВГ (1) x 2.57 2.58 (2) y 1.45 1.46 (3) z 8.33 8.34 (1)+(2) x+y 4.02 4.04 (1)-(2) x-y 1.11 1.13 9.24 9.43 2.28 2.35 §8. Математические модели и численные методы.Велика роль математики в решении задач реального мира. Физиков математика интересует не сама по ...
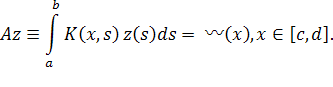





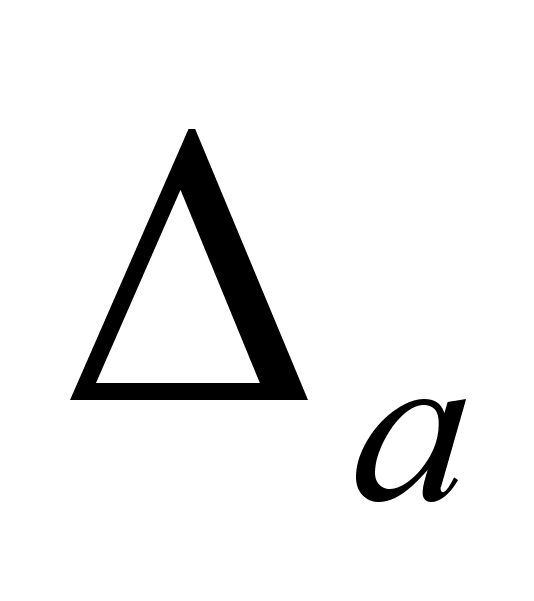
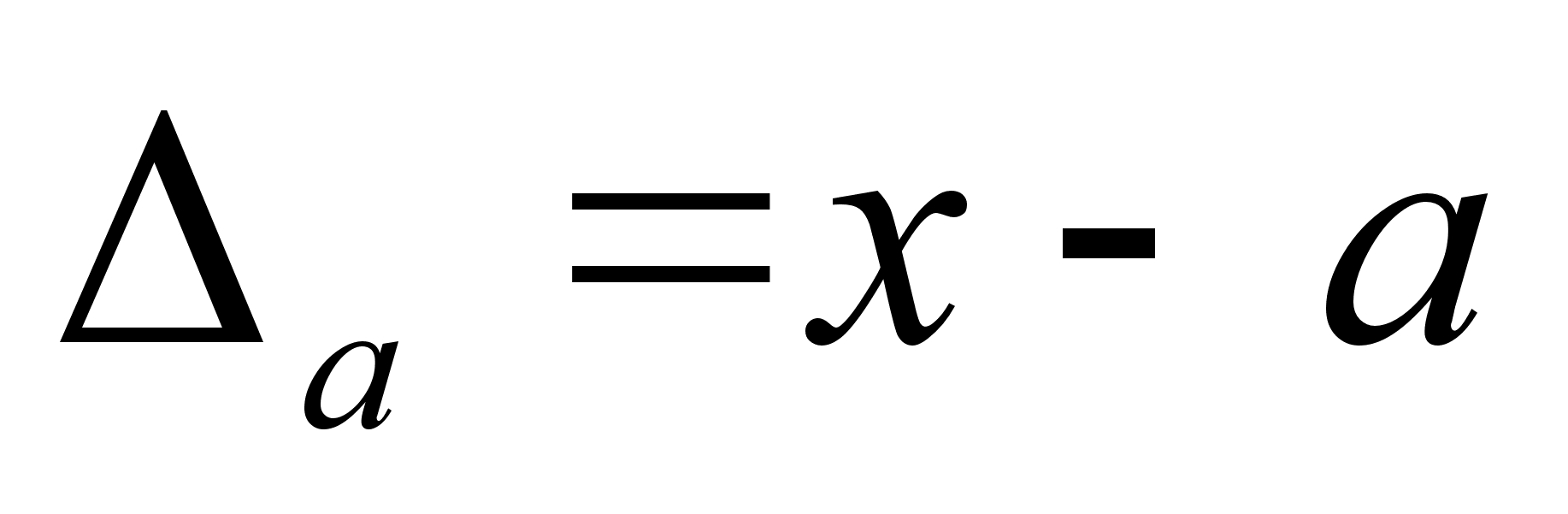
0 комментариев