Навигация
Классификация нецентральных поверхностей второго порядка
2. Классификация нецентральных поверхностей второго порядка.
Пусть S — нецентральная поверхность второго порядка, т. е. поверхность, для которой инвариант I3 равен нулю. Произведем стандартное упрощение уравнения этой поверхности. В результате уравнение поверхности примет вид
a´11х´2 + а´22у´2 + a´33z´2 + 2а´14 x´ + 2а´24у´+2а´34z´ +а´44 = 0 (7)
для системы координат Ox´y´z´
Так как инвариант I3 = 0 и его значение, вычисленное для уравнения (7) , равно
a´11 • а´22 • a´33, то один или два из коэффициентов a´11 , а´22 , a´33равны нулю. В соответствии с этим рассмотрим следующие возможные случаи.
![]()
Ä 1°. Один из коэффициентов a´11
, а´22 , a´33 равен нулю. Ради определенности будем считать, что a´33 = 0 (если равен нулю какой-либо другой из указанных коэффициентов, то можно перейти к рассматриваемому случаю путем переименования осей координат). Перейдем от координат х', у', z' к новым координатам х, у, z по формулам
Подставляя х', у' и z', найденные из (8), в левую часть (7) и заменяя затем
a´11на a11 , а´22 на а22 , а´34 на p и а´44 на q , получим следующее уравнение поверхности S в новой системе координат Oxyz :
a11х2 + а22у2 + 2pz + q = 0 (9)
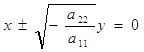 |
1) Пусть р = 0, q = 0. Поверхность S распадается на пару плоскостей
При этом, очевидно, эти плоскости будут мнимыми, если знаки a11 и а22одинаковы, и вещественными, если знаки a11 и а22 различны.
2) Пусть р = 0, q ≠ 0. Уравнение (9) принимает вид
a11х2 + а22у2 + q = 0 (10)
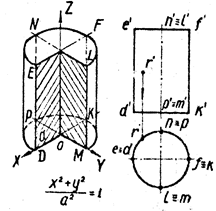
Известно, что уравнение (10) является уравнением цилиндра с образующими, параллельными оси Оz. При этом если a11 , а22 , q имеют одинаковый знак, то левая часть (10) отлична от нуля для любых х и y, т. е. цилиндр будет мнимым. Если же среди коэффициентов a11 , а22 , q имеются коэффициенты разных знаков, то цилиндр будет вещественным. Отметим, что в случае, когда a11 и а22 имеют одинаковые знаки, a q — противоположный, то величины
![]()
положительны.
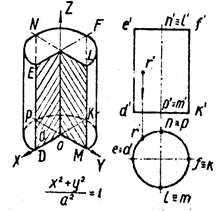
Обозначая их соответственно через а2 и b2, мы приведем уравнение (10) к виду
![]()
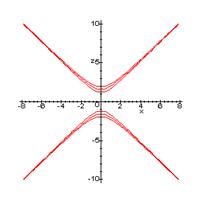
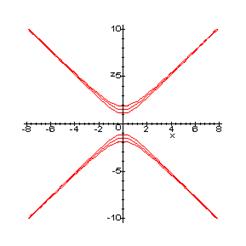
Таким образом, в отмеченном случае мы имеем эллиптический цилиндр. В случае, a11 и а22 имеют различные знаки, мы получим гиперболический цилиндр. Легко убедиться, что уравнение гиперболического цилиндра может быть приведено к виду
![]()
3) Пусть р≠0. Произведем параллельный перенос системы координат, выбирая новое начало в точке с координатами
![]()
(0, 0, ).
При этом оставим старые обозначения координат х, у, z. Очевидно, для того чтобы получить уравнение поверхности S в новой системе координат, достаточно заменить в уравнении (9)
![]()
Получим следующее уравнение:
a11х2 + а22у2 + 2pz = 0 (13)
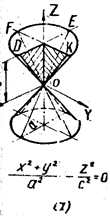
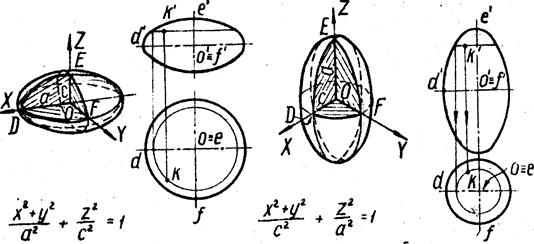
Уравнение (13) определяет так называемые параболоиды. Причем если a11 и а22 имеют одинаковый знак, то параболоид называется эллиптическим. Обычно уравнение эллиптического параболоида записывают в канонической форме:
![]()
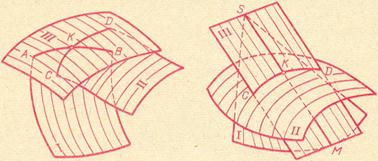
Уравнение (14) легко получается из (13). Если a11 и а22 имеют разные знаки, то параболоид называется гиперболическим. Каноническое уравнение гиперболического параболоида имеет вид
![]()
Это уравнение также легко может быть получено из (13).
Ä 2°. Два из коэффициентов a´11 , а´22 , a´33 равны нулю. Ради определенности будем считать, что a´11 = 0 и а´22 = 0 Перейдем от х,', у', z' к. новым координатам х, у, z по формулам :
![]()
Подставляя х', у' и z' , найденные из (16) в левую часть (7) и заменяя затем a´33 на a33 , a´14 на р , a´24 на q и a´44 на r , получим следующее уравнение поверхности S в новой системе координат Охуz :
a33 z2 + 2px + 2qy + r = 0 (17)

1) Пусть р=0, q=0. Поверхность S распадается на пару параллельных плоскостей
При этом, очевидно, эти плоскости будут мнимыми, если знаки a33 и r одинаковы, и вещественными, если знаки a33 и r различны, причем при r = 0 эти плоскости сливаются в одну.
2) Хотя бы один из коэффициентов р или q отличен от нуля. В этом случае повернем систему координат вокруг оси Oz так, чтобы новая ось абсцисс стала параллельной плоскости 2рх+2qy+r=0. Легко убедиться, что при таком выборе системы координат, при условии сохранения обозначения х, у и z для новых координат точек, уравнение (17) примет вид
a33 z2 + 2q´y = 0 (19)
которое является уравнением параболического цилиндра с образующими, параллельными новой оси Ох.
§ 3. Исследование формы поверхностей второго порядка по их каноническим уравнениямПохожие работы
... фигур, которое может задавать данное уравнение, построили график эллипса в общей и канонической системе координат. Часть II. Исследование поверхности второго порядка 1. Определение типа поверхности Для данного уравнения поверхности второго порядка: 4x2 - z2 + 12xz + 6y - 8z + 5 = 0 (4.1) Определить тип поверхности с помощью инвариантов. 4 + 0 -1 = 3 = ...
... кривой второго порядка и приведя его к каноническому виду, мы установили, что данная кривая — эллипс. Мы получили каноническое уравнение гиперболы при помощи преобразований параллельного переноса и поворота координатных осей. Исследование формы поверхности второго порядка Теоретическая часть Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные ...
... линию называют образующей. Она может быть прямой, тогда образованную ей поверхность относят к классу линейчатых. Если образующая – кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности. Определителем поверхности называют совокупность условий, задающих поверхность в пространстве. ...
... поверхности, которые в пересечении с данными поверхностями дают простые для построения линии (например, прямые или окружности). В общем случае вспомогательные секущие плоскости применяют и для построения линии пересечения кривой поверхности гранной. Изложенный общий способ построения линии пересечения одной поверхности другою не исключает применения другого способа, если хотя бы одна из этих ...
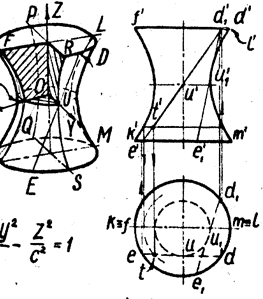
0 комментариев