Навигация
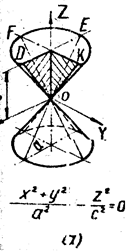
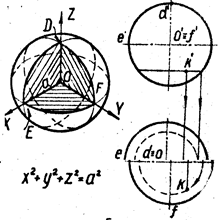
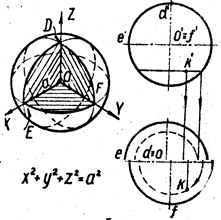
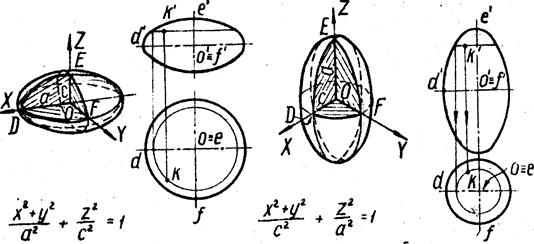
Из уравнения (3) вытекает, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат—центром симметрии. Числа а, b, с называются полуосями эллипсоида и представляют собой длины отрезков, от начала координат до точек пересечения эллипсоида с осями координат. Чтобы более наглядно представить себе форму эллипсоида, выясним форму линий пересечения его плоскостями, параллельными какой-либо из координатных плоскостей.
Ради определенности рассмотрим линии Lh пересечения эллипсоида с плоскостями
z = h (20)
параллельными плоскости Оху. Уравнение проекции L*hлинии Lh на плоскость Оху получается из уравнения (3), если положить в нем z = h. Таким образом, уравнение этой проекции имеет вид
![]()
![]()
Если положить
то уравнение (21) можно записать в виде
![]()
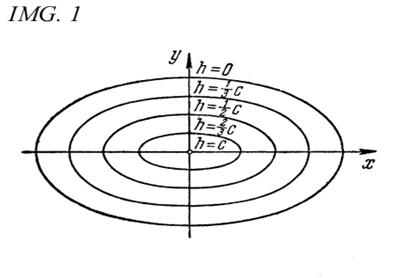 |
т. е. L*hпредставляет собой эллипс с полуосями а* и b*, которые могут быть вычислены по формулам (22). Так как Lh получается «подъемом» L*h на высоту h по оси Оz (см. (20)), то и Lh представляет собой эллипс.
Представление об эллипсоиде можно получить следующим образом. Рассмотрим на плоскости Оху семейство эллипсов (23) (рис. 1), полуоси а* и b* которых зависят от h (см. (22)), и каждый такой эллипс снабдим отметкой h, указывающей, на какую высоту по оси Оz должен быть «поднят» этот эллипс. Мы получим своего рода «карту» эллипсоида. Используя эту «карту», легко представить себе пространственный вид эллипсоида.
(Метод представления формы фигуры путем получения «карты» фигуры я привожу только для эллипсоида, представить форму других фигур этим методом можно аналогично)
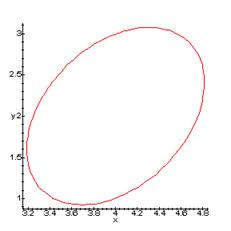
Наглядное изображение эллипсоида находится на следующей странице.
Эллипсоид 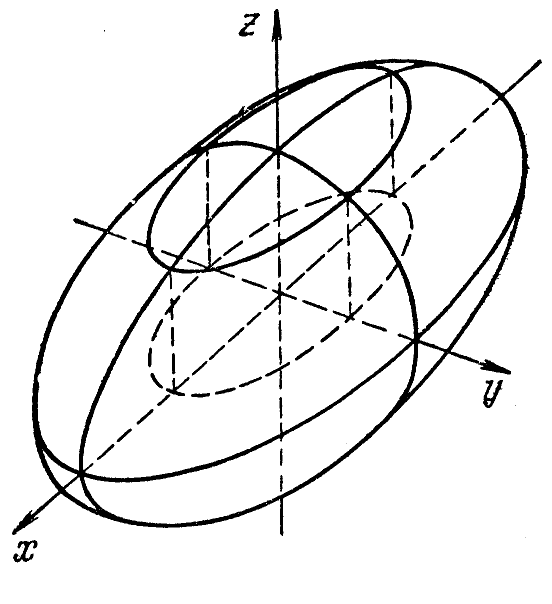
.
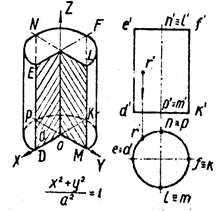
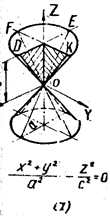
2. Гиперболоиды.
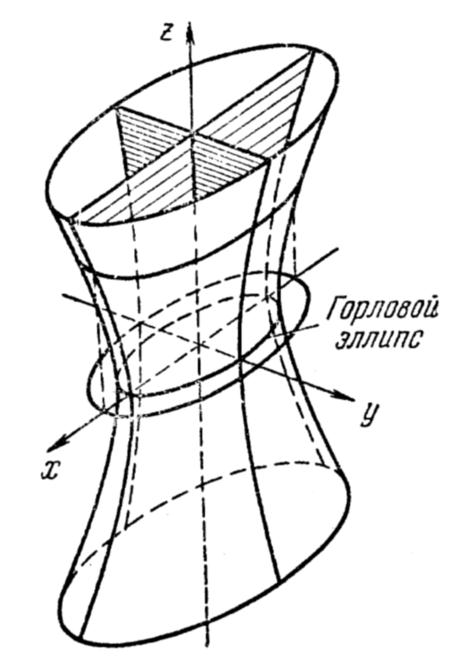
Ä 1°. Однополостный гиперболоид. Обратимся к каноническому
![]() уравнению (4) однополостного гиперболоида
уравнению (4) однополостного гиперболоида
Из уравнения (4) вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида.
![]() Ä 2°. Двуполостный гиперболоид.
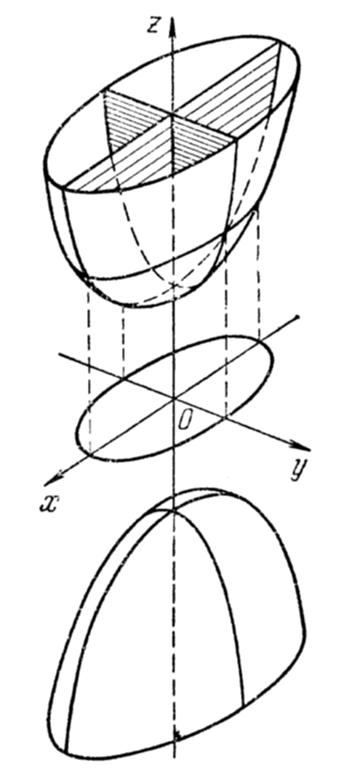
Ä 2°. Двуполостный гиперболоид.
Из канонического уравнения (5) двуполостного гиперболоида вытекает, что координатные плоскости являются его плоскостями симметрии, а начало координат — его центром симметрии.
3. Параболоиды.
Ä 1°. Эллиптический параболоид. Обращаясь к каноническому уравнению (14) эллиптического параболоида
![]()
мы видим, что для него Oxz и Оуz являются плоскостями симметрии. Ось Oz, представляющая линию пересечения этих плоскостей, называется осью эллиптического параболоида.

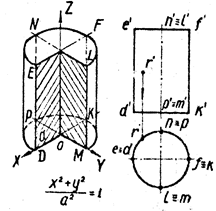
![]() Ä 2°. Гиперболический параболоид. Из канонического уравнения (15)
Ä 2°. Гиперболический параболоид. Из канонического уравнения (15)
гиперболического параболоида вытекает, что плоскости Oxz и Оуz являются плоскостями симметрии. Ось Oz называется осью гиперболического пaраболоида.
Прим.: получение «карты высот» для гиперболического пaраболоида несколько отличается от аналогичной процедуры для вышеприведенных поверхностей 2-го порядка, поэтому я также включил его в свой реферат.
Линии z=h пересечения гиперболического параболоида плоскостями z=h представляют собой при h>0 гиперболы
![]()
с полуосями
![]()
![]() а при h < 0 —сопряженные гиперболы для гипербол (24)
а при h < 0 —сопряженные гиперболы для гипербол (24)
с полуосями
![]()
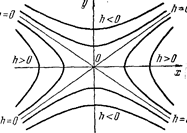 Используя формулы (24)—(27), легко построить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым :
Используя формулы (24)—(27), легко построить «карту» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым :
Из формул (25) и (27) вытекает, что прямые (28) являются асимптотами гипербол (24) и (26).
Карта гиперболического параболоида дает представление о его пространственной форме. Как и в случае эллиптического параболоида, можно убедиться в том, что гиперболический параболоид может быть получен путем параллельного перемещения параболы, представляющей собой сечение плоскостью Oxz (Оуz), когда ее вершина движется вдоль параболы, являющейся сечением параболоида плоскостью Oyz (Oxz).
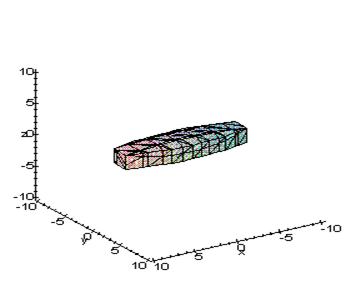
Прим.: Изображение гиперболического пaраболоида дано на следующей странице.
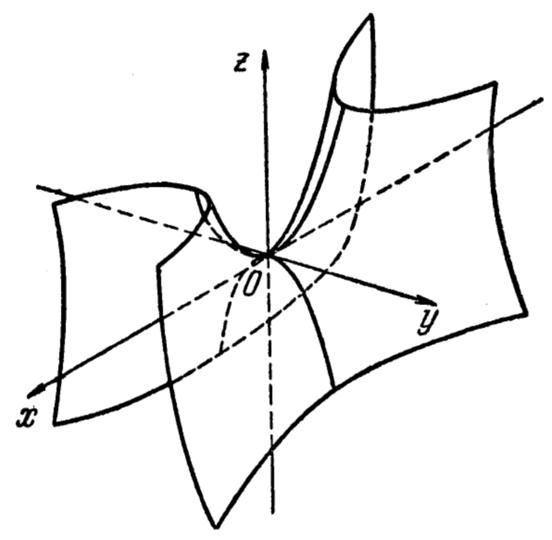
Гиперболический параболоид.
4. Конус и цилиндры второго порядка.
![]() Ä 1°. Конус второго порядка
Ä 1°. Конус второго порядка
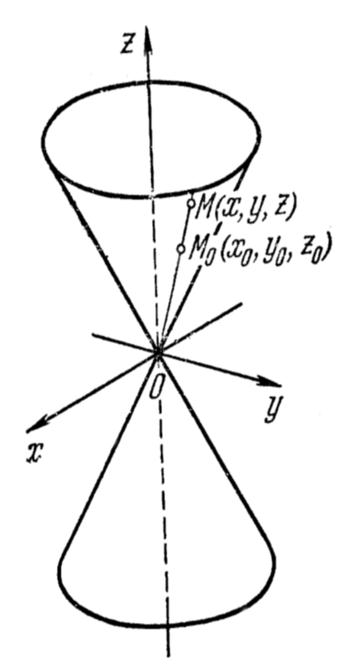
Убедимся, что вещественный конус S образован прямыми линиями, проходящими через начало О координат. Естественно называть точку О вершиной конуса.
Для доказательства сформулированного утверждения, очевидно, достаточно установить, что прямая L, соединяющая произвольную, отличную от начала координат точку
М0(х0, у0, z0) конуса (6) и начало координат О , целиком располагается на конусе, т. е. координаты (х, у, z) любой точки М прямой L удовлетворяют уравнению (6).
![]() Так как точка М0(х0, у0, z0) лежит на конусе (6), то :
Так как точка М0(х0, у0, z0) лежит на конусе (6), то :
Координаты (х, у, z) любой точки М прямой L равны соответственно tx0, ty0 , tz0, где t—некоторое число. Подставляя эти значения для х, у и z в левую часть (6), вынося затем t2 за скобку и учитывая (29), мы убедимся в том, что М лежит на конусе. Таким образом, утверждение доказано. Представление о форме конуса может быть получено методом сечений. Легко убедиться, что сечения конуса плоскостями z = h представляют собой эллипсы с полуосями :
Ä 2°. Эллиптический цилиндр.
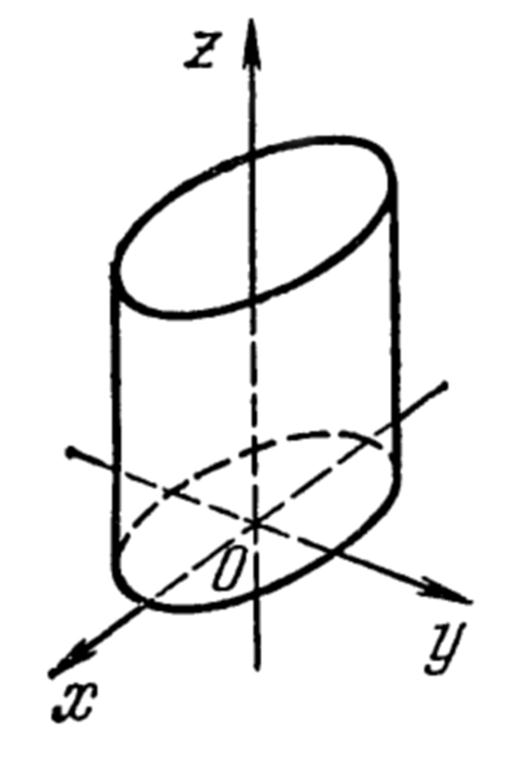 |
Состоит из прямых линий, параллельных оси Oz .
![]() Ä 3°. Гиперболический цилиндр.
Ä 3°. Гиперболический цилиндр.
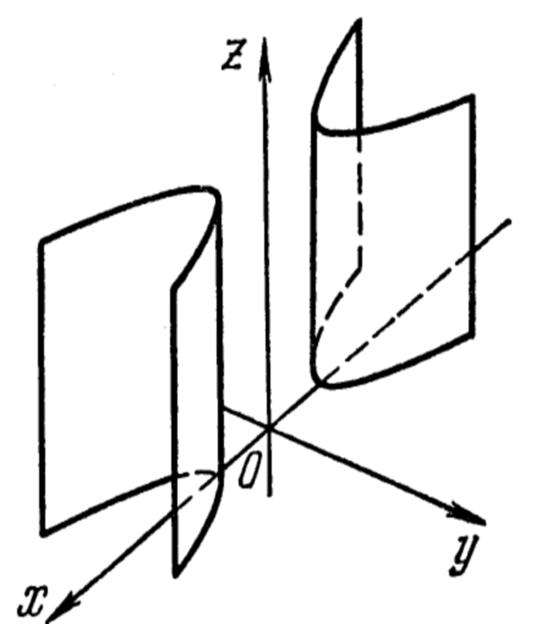
Состоит из прямых линий, параллельных оси Oz .
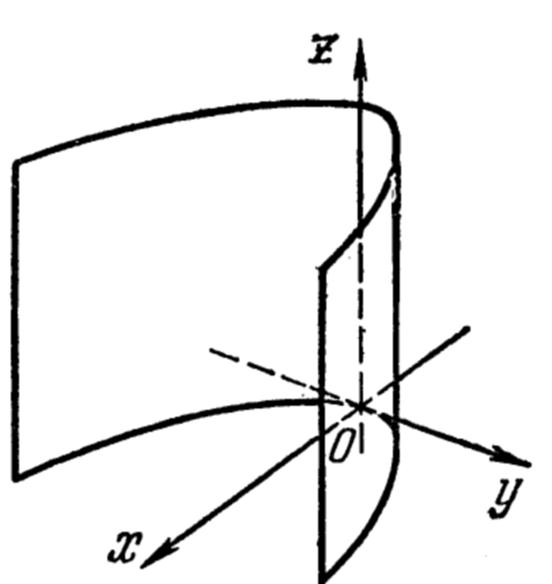
Ä 4°. Параболический цилиндр.
a33 z2 + 2q´y = 0 (19)
Путем переименования осей координат и простых арифметических операций из уравнения, (19) мы получим новое, компактное уравнение параболического цилиндра.
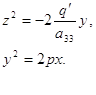
![]()
Похожие работы
... фигур, которое может задавать данное уравнение, построили график эллипса в общей и канонической системе координат. Часть II. Исследование поверхности второго порядка 1. Определение типа поверхности Для данного уравнения поверхности второго порядка: 4x2 - z2 + 12xz + 6y - 8z + 5 = 0 (4.1) Определить тип поверхности с помощью инвариантов. 4 + 0 -1 = 3 = ...
... кривой второго порядка и приведя его к каноническому виду, мы установили, что данная кривая — эллипс. Мы получили каноническое уравнение гиперболы при помощи преобразований параллельного переноса и поворота координатных осей. Исследование формы поверхности второго порядка Теоретическая часть Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные ...
... линию называют образующей. Она может быть прямой, тогда образованную ей поверхность относят к классу линейчатых. Если образующая – кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности. Определителем поверхности называют совокупность условий, задающих поверхность в пространстве. ...
... поверхности, которые в пересечении с данными поверхностями дают простые для построения линии (например, прямые или окружности). В общем случае вспомогательные секущие плоскости применяют и для построения линии пересечения кривой поверхности гранной. Изложенный общий способ построения линии пересечения одной поверхности другою не исключает применения другого способа, если хотя бы одна из этих ...
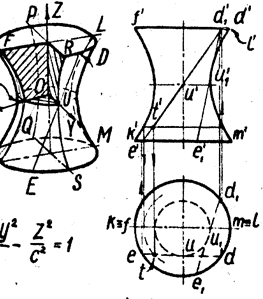
0 комментариев