Величина определителя равна сумме произведений элементов любой строки (столбца) на соответствующее алгебраическое дополнение этих элементов

6.   Величина определителя равна сумме произведений элементов любой строки (столбца) на соответствующее алгебраическое дополнение этих элементов.

Например, 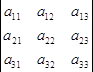 = а₁₁*А₁₁ +а₁₂*А₁₂+а₁₃*А₁₃; правая часть равенства называется разложением определителя по элементам первой строки.

7.   Сумма произведений элементов строки на алгебраические дополнения к элементам другой строки равна нулю.

Например, а₁₁ А₂₁+а₁₂А₂₂+а₁₃А₂₃=0.

Перечисленные свойства определителей справедливы для определителей любого порядка.

Пример. Вычислить определитель 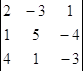 двумя способами.

первый способ. 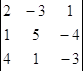 = 2*5*(-3)+(-3)*(-4)*4+1*1*1 – (4*5*1+1*(-4)*2 + +(-3)*(-3)*1) = -30+48+1 – (20 – 8+9) = 19 – 21= -2.

Второй способ. Разложим определитель по элементам второго столбца. 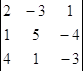 = -3 А₁₂ + 5А₂₂ + 1А₃₂ = -3(-1)¹⁺² + 5(-1)²⁺² +(-1)³⁺² = -3*(-1)*(-3+16)+5(-6-4) – (-8 – 1) = 3*13+5*(-10) +9 = 48 – 50 = -2.

Системы линейных алгебраических уравнений. Решение систем по формулам Крамера.

Система линейных алгебраических уравнений имеет вид:

 а₁₁х₁ + а₁₂х₂ + а₁₃х₃ = в₁

 а₂₁х₁ + а₂₂х₂ + а₂₃х₃ = в₂

 а₃₁х₁ + а₃₂х₂ + а₃₃х₃ = в₃

Это система трех уравнений с тремя неизвестными х₁, х₂, х₃. Вещественные числа а_ij (i = , j = ) называются коэффициентами системы. в₁, в₂, в₃ – свободные члены. Если хотя бы одно из чисел в₁, в₂, в₃, отлично от нуля, система называется неоднородной. Если все свободные члены равны нулю, то система имеет вид:

 а₁₁х₁ + а₁₂х₂ + а₁₃х₃ = 0

 а₂₁х₁ + а₂₂х₂ + а₂₃х₃ = 0

 а₃₁х₁ + а₃₂х₂ + а₃₃х₃ = 0

и называется однородной.

По формуле Крамера решаются только неоднородные системы.

Определитель системы Δ называется определитель, составленный из коэффициентов системы:

Δ =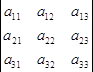

Если определитель системы Δ не равен 0, то система имеет единственное решение, которое находится по формулам:

Х₁ = Δх₁/ Δ; х₂== Δх₂/ Δ; х₃== Δх₃/ Δ; где

Δх₁= 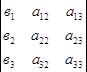 ; Δх₂= 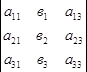; Δх₃= .

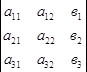Если определитель системы = Δ равен нулю, и хотя бы один из определителей ∆х₁=∆х₂=∆х₃ отличен от нуля, то система несовместна.

Если определитель системы ∆=0, и ∆х₁=∆х₂=∆х₃=0, то система имеет бесконечное множество решений. (неопределенная система).

Пример. Решить систему уравнений:

Х + 2у – z = 1

-3х + у = 2z = 0

х + 4у + 3z = 2

1)   Вычислим определитель системы ∆ = 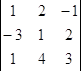 = 1*1*3+2*2*1+(-1)*4*(-3) – (1*1*(-1)+4*2*1+3*2*(-3))=3+4+12 – (-1 + 8 – 18) = 19+11 = 30.

Система имеет единственное решение, т.к. определитель ∆ = 30 ≠ 0.

2)   Вычислим определители ∆х, ∆у, ∆z.

∆х = 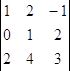 = 5; ∆у =  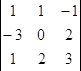= 13; ∆z =  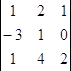= 1.

3)   По формулам Крамера находим решение системы:

Х = ∆х/∆ = 5/30 = 1/6; у = ∆у/∆ = 13/30; z = ∆z/∆ = 1/30;

Ответ: решение системы (1/6; 13/30; 1/30).

По формулам Крамера можно решить систему n линейных уравнений с n неизвестными.

Пример Решить систему уравнений.

х - у+z=1

х + у – z=2

5х + у – z=7

1)   Составим и вычислим определитель системы ∆= 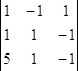 = 0.

2)   Вычислим определители ∆х, ∆у, ∆z.

 ∆х =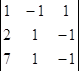 = 0, ∆у =  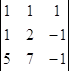= -2

Т.к. определитель ∆у= -2 ≠ 0, мы делаем заключение: Система несовместна, т.е. она не имеет решения.

 Тема 7. Алгебра матриц.

Определение. Таблица, составленная из m*n чисел называется матрицей размерности m*n,

 а₁₁ а₁₂ а₁₃…а_1п

а₂₁ а₂₂ а₂₃…а_2п

……………… = А_м*п= //а_ij//

а_м1 а_м2 а_м3…а_мп , где

m – число строк, n – число столбцов. Числа а_ij называются элементами матрицы, i- номер строки, j – номер столбца, на пересечении которых стоит элемент.

Разновидности матриц.

1.   Матрица называется прямоугольной, если m≠n.

2.   Матрица называется квадратной, если m=n.

3.   Матрица называется матрицей - строкой, если m=1.

4.   Матрица называется матрицей - столбцом, если n=1.

Например, 1) 1 2 3 = А_2*3 – прямоугольная матрица размерности 2*3 (два на три)

0 –1 5

2) 1 2 - квадратная матрица.

3 4

3)   (1 0 3 5, -1) – матрица строка.

4)    7

12 матрица столбец.

5

3

5)   Квадратная матрица называется треугольной, если все элементы матриц, расположенные выше или ниже главной диагонали равны нулю.

Например, 1 0 0 5 1 –3

2 6 0 или 0 4 2

-1 –2 8 0 0 -1

6)   Квадратная матрица называется диагональной, если все ее элементы, кроме элементов главной диагонали, равны нулю.

Например, 1 0 0

0 –2 0

0    0 5

7)   Квадратная матрица называется единичной, если элементы диагональной матрицы, стоящие на главной диагонали равны единице.

1 0 0

Е = 0 1 0

0 0 1 .

Алгебра матриц.

1.   Равенство матриц. Две матрицы А_м*п и В_м*п одинаковой размерности равны, если равны соответствующие элементы этих матриц.

А_м*п = В_м*п ó а_ij = b_ij (i = , j = )

ó этот знак (квантор эквивалентности) заменяет слова «тогда и только тогда»,

обозначение (i = ) применяется, если хотят сказать, что i пробегает все значения от 1 до m.

2. Сумма матриц. Суммой двух матриц А_м*п = //а_ij// и В_м*п = //в_ij// называется матрица С_м*п, элементы которой С_ij = а_ij + в_ij . C_m*n = A_m*n + B_m*n. Складывать можно матрицы одинаковой соразмерности.

Нпример, Если А= 1 –2 4 В= -3 2 5

3 1 –6 , 1 –6 4 , то

=

=

+

А+В = 1 –2 4 -3 2 5 1-3 -2+2 4+5 -2 0  9

3 1 –6 1 –6 4 , 3+1 1-6 6+4 4 –5 –2

3. Умножение матрицы на число. Для того чтобы умножить матрицу на число надо каждый элемент матрицы умножить на это число.

3 2 4 –1 -2 1 5 6

αА = //α a_ij//.

12 8 16 –4  -8 4 20 24

3 2 4 –1 -2 1 5 6

Например, вычеслить 4 А, если А =

=

4А = 4 *

4. Умножение матриц. Произведением матрицы А_м*е на матрицу В_е*п называется матрица С_м*п (А_м*е*В_е*п=С_м*п), элементы которой получаются по правилу «Строка на столбец»:

с_ij =a_ijb_ij + a_i2b_2j +…+ a_ieb_ej

(i= ; j= ) , т.е. для вычисления с_ij следует элементы i – строки левой матрицы А_м*е умножить на соответствующие элементы j –го столбца правой матрицы В_е*п и полученные произведения сложить.

Замечание 1. Из этого определения следует, что произведение матриц имеет смысл тогда, когда число столбцов первого сомножителя равно числу строк второго сомножителя.

1 2  2 4  3 1

3 4 1 3  2 –1 –2 4

Замечание 2. Если имеют смысл АВ и ВА, то как правило, АВ≠ВА.

Пример. Вычислить АВ, если А =  В =

Решение: АВ=С

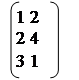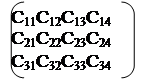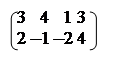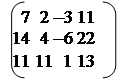
С= * = =

С11=1*3+2*2=7;	С12=1*4+2*(-1)=2	С13=1*1+2*(-2)= -3	С14=1*3+2*4=11
С21=2*3+4*2=14;	С22=2*4+4*(-1)=4	С23=2*1+4*(-2)= -6	С24=2*3+4*4=22
С31=3*3+1*2=11	С32=3*4+1(-1)=11	С33=3*1+1*(-2)=1	С34=3*3+1*4=13

7 2 –3 11 14 4 –6 22 11 11 1 13

Ответ: А*В=С=

Пример. Найти произведения двух матриц АВ и ВА, если А = 1 2  ,

В = 2 1 3 4

1 3

Сравним эти произведения.

*

=

1) С=АВ= 1 2 2 1 4 7

3 4 1 3 10 15

С₁₁ = 1*2+2*1=4; С₁₂ = 1*1+2*3=7;

С₂₁ = 3*2+4*1=10; С₂₂ = 3*1+4*3=15

=

*

2) Д=ВА= 2 1 1 2 5 8

1 3 3 4 10 14

d₁₁=2*1+1*3=5; d₁₂=2*2+1*4=8

d₂₁=1*1+3*3=10; d₂₂=1*2+3*4=14

Мы убедились, что в нашем примере АВ≠ВА.

Пример. Вычислить АВ, если А=(4 0 -2 1); В= 

Решение: АВ=(4 0 -2 1)*  =4*3+0*1+(-2)*5+1*(-2)=(0)

Ответ: АВ=(0) – нуль – матрица.

Замечание. При умножении матрицы строки на матрицу столбец получается матрица из одного элемента – число.

5. Транспонирование матрицы. Если в матрице А строки заменить столбцами, то новая матрица называется транспонированной по отношению к матрице А и обозначается символом А^т. Замечание (А^т)^т=А.