Навигация
A x а х
0 a x а х
Рис.1 Рис.2
 y
y
![]()

 f(a)
f(a)
![]()
![]()
 f(a)
f(a)
![]()
![]()
![]()
![]()
0 a x 0 a x
Рис.3 Рис.4
На приведенных рисунках предел существует в случаях 1) и 2), причем во 2) значение функции в точке а не совпадает с предельным, а в 1) совпадает f(a) = b . На рисунках 3) и 4) предел у функции в точке а не существует.
|
Все элементарные функции непрерывны в каждой точке, где они определены.
Основные теоремы о пределах функций.
1. Предел суммы двух функций равен сумме пределов.
|
|
|
2. Предел произведения двух функций равен произведению пределов.
|
|
|
3. Предел произведения числа на функцию равен произведению числа на предел функции.
|
|
Это свойство можно записать так: постоянный множитель выносится за знак предела.
4. Предел отношения двух функций равен отношению пределов этих функций. (Кроме случая, когда знаменатель стремиться к нулю).
|
|
|
|
Если знаменатель стремиться к нулю, а числитель - нет, то говорят, что отношение стремиться к бесконечности.
Бесконечность – это не число, ее можно добавить ко множеству вещественных чисел R в качестве нового элемента ∞. После этого числовая прямая превращается в так называемую расширенную прямую.
Раз мы добавили новый элемент ко множеству вещественных чисел, то запишем арифметические операции с этим элементом ∞.
Пусть а любое вещественное число, а Є R, тогда
| а + ∞ = ∞ | -∞ + а = -∞ | ∞ * (-а) = - ∞, а › 0 |
| ∞ - а = ∞ | -∞ - а = - ∞ | ∞ * ∞ = ∞ |
| а * ∞ = ∞, а ≠ 0 | ∞ + ∞ = ∞ | а/∞ = 0, ∞/а = ∞ |
| - ∞ - ∞ = - ∞ |
Есть особые случаи, когда предел суммы, произведения или частного нельзя найти, зная только пределы слагаемых, сомножителей или делимого и делителя. Такие случаи называются неопределенностями.
Выделяют неопределенности двух типов:
Арифметические неопределенности (0/0); (00/00); (00 – 00); (0 * 00).
Степенно-показательные неопределенности (100); (000); 00.
Эти записи не являются операциями над числами и 00, они представляют собой только деловые обозначения.
В случае неопределенности предел может быть равен нулю, конечному числу, бесконечности или не существовать. Для нахождения предела (раскрытие неопределенности) надо исследовать каждый случай отдельно.
|
Решение:
|
= (4 – 4) / (4 – 2 – 2) = (0/0).
|
|
|
Решение:
|
|
|
|
|
|
Для раскрытия неопределенностей используются не только различные приемы преобразования функций, как мы видели в примерах 1 и 2, но и так называемые замечательные пределы.
|
|
иррациональное «непперово» число. Это число часто берут за основание логарифма, тогда такой логарифм обозначается так: log℮x = lnx и называется натуральным логарифмом.
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема 11. Производная и дифференциал.
Приращение аргумента, приращение функции.
|
у Рис.1
| ||||
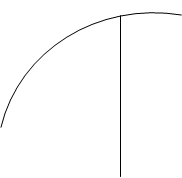 | ||||
Δу
 | |||
| |||
х0 х0 + Δх
Производная функция у = f(х), в точке х0 определяется как предел отношения приращения функции Δу к приращению аргумента Δх, при стремлении Δх к нулю. f `(x0) = lim (Δf/Δx). Этот предел будет иметь конечное значение, если только и числитель стремиться к нулю (приращение функции Δf→0).
Производная имеет смысл скорости изменения какого – либо показателя. Дифференциал определяется как главная линейная часть приращения функции. Дифференциал показывает, как изменялась бы величина, если бы скорость ее изменения была бы постоянной. Дифференциал для функции у=f(х) обозначается через dy или df. Вычисляется он по формуле dy=f `(x)dx, где f ` (x) – производная функция f(x), а dx – число равное приращению независимой переменной (аргумента) ∆х.
Для вычисления производной выведены правила нахождения производной и таблицы производных элементарных функций. Функция, имеющая производную в точке х, называется дифференцируемой в этой точке. Если функция имеет производную в каждой точке интервала, то она называется дифференцируемой в интервале.
Правила дифференцирования функций.
Пусть U(х) и V(х) дифференцируемы в точке х.
1. (U(x) + V(x))` = U`(x) + V`(x)
2. (U(x) * V(x))` = U`(x) * V`(x) + V`(x) * U`(x)
3. (C*U(x))` = CU`(x), C - const
4. (U(x) / V(x))` = [U`(x) * V(x) - V`(x) * U(x)]/ V2(x)
Таблица производных.
1. C` = 0, C – const.
2. x` = 1
3. (xα)` = α xα – 1, α Є R
4. (ax)` = ax lnx, a>0 , a≠1
5. (ln x)` = 1/x
6. (sin x)` = cos x
7. (cos x)` = - sin x
8. (tg x)` = 1/(cos x)2
9. (ctg x)` = - 1/(sin x)2
10. (arcsin x)` = 1/![]() 2)
2)
11. (arccos x)` = - 1/![]() 2)
2)
12. (arctg x)` = 1/(1 + x2)
13. (arcctg x)` = - [1/(1 + x2)]
правила для нахождения дифференциала можно написать самим, умножив соответствующее правило взятия производной на dx.
Например: d sinx = (sinx)`dx = cosx dx.
Пример 1. Найти приращение функции f(x) = x2, если х = 1, ∆х = 0,1
Решение: f(х) = х2, f(х+∆х) = (х+∆х)2
Найдем приращение функции ∆f = f(x+∆x) – f(x) = (x+∆x)2 – x2 = x2+2x*∆x+∆x2 – x2 = 2x*∆x + ∆x2/
Подставим значения х=1 и ∆х= 0,1, получим ∆f = 2*1*0,1 + (0,1)2 = 0,2+0,01 = 0,21
Пример 2. Найти производную функции f(x) = x2, в произвольной точке х по определению производной, т.е. не используя таблицу производных.
|
Из первого примера ∆f = 2x*∆x+∆x2, подставим, получим
|
|
|
Пример 3. у = 1-х, Найти ∆у при х=2, ∆ = 0,1
Решение: у(х) = 1-х, у(х+∆х) = 1 – (х+∆х),
∆у = у (х+∆х) – у(х) = 1-х - ∆х – (1 – х) = 1-х - ∆х – 1 + х = - ∆х
при х = 2, ∆х = 0,1 ∆у = -∆х = -0,1.
Пример 4. Найти производную от функции у=3х4 – 2х2 + 1.
Решение у` = 3*4х3 – 2*2х + 0 = 12х3 – 4х.
Пример 5. Найти производную от функции у = x2 *℮х.
Решение: у` = (x2)` *℮х + x2 *(℮х)` = 2x ℮х + x2 *℮хln℮
ln ℮ = log℮℮ = 1. y` = 2x℮x + x2 * ℮x
Пример 6. У = х/(х2+1). Найти у`.
Решение у` = [1*(х2+1) – х*2х] / (х2+1)2 = [х2+1 – 2х2] / (x2 +1)2 = (1-x2) / (x2+1)2
Производные от сложных функций.
Формула для нахождения производной от сложной функции такова:
[f (φ(х))]` = fφ`(φ(x)) * φ`(x)
Например: у = (1-х2)3; у`= 3(1 –х2)2 * (-2х) или у = sin2х; у` = 2sinx * cosx.
Пример 7 . Найти dy, если у = sin 3х
Решение dy = у` * dx = (sin3x)` dx = (cos3x) * 3dx = 3 cos3x dx.
Пример 8. Найти dy, если у = 2х^2/
Решение: dy = y` * dx = (2x^2)` * dx = 2x^2 ln2 * 2xdx
Производные высших порядков.
Пусть мы нашли от функции у = f(х) ее производную у` = f `(х). Производная от этой производной и называется производной второго порядка от функции f(х) и обозначается у`` или f `` (х) или (d2y) / (dx2). Аналогично определяются и обозначаются: производная третьего порядка у``` = f ```(x) = (d3y) / (dx3).
производная четвертого порядка уIV = f IV(x) = (d4y) / (dx4).
производная n-oго порядка у(n) = f (n)(x) = (d n y) / (dxn).
Пример: у = 5х4 – 3х3 + 2х – 2. Найти у``.
Решение. Находим в начале первую производную: у` = 20х3 – 9х2 +2, потом вторую от первой производной: у`` = 60х2 – 18х.
Пример. y=хsinx. Найти у```.
Решение. y` = sinx + xcosx
y`` = cosx + cosx – x sinx = 2cosx – x sinx
y``` = -2sinx – sinx – x cosx = -3sinx – x cosx.
Тема 12. Понятие первообразной. Неопределенный интеграл. Свойства неопределенного интеграла.
Определение. Функция F(x) называется первообразной для функции f(x) на интервале Х, если в каждой точке этого интервала выполняется условие
F ` (x)=f(x).
Например, для функции f(x) = 2х первообразной является F(х) = х2 для любых х Є (-∞, ∞).
Действительно, F`(x) = 2x = f(x).
F1(x) = x2 + 2 так же является первообразной для f(x) = 2x, F2(x) = x2 – 100 первообразная той же функции f(x) = 2x.
Теорема. Если F1(x) и F2(x) первообразные для функции f(x) на некотором интервале Х, то найдется такое число С, что справедливо равенство:
F2(x) = F1(x) + C,
Или можно сказать так, две первообразные для одной и той же функции отличаются друг от друга на постоянное слагаемое.
Определение. Совокупность всех первообразных для функции f(x) на интервале Х называется неопределенным интегралом от функции f(x) и обозначается ![]() f(x)dx, где
f(x)dx, где ![]() - знак интеграла, f(x) – подинтегральная функция, f(x)dx – подинтегральное выражение. Таким образом
- знак интеграла, f(x) – подинтегральная функция, f(x)dx – подинтегральное выражение. Таким образом
![]() f(x)dx = F(x) + C,
f(x)dx = F(x) + C,
F(x) – некоторая первообразная для f(x), С – произвольная постоянная. Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Основные свойства неопределенного интеграла.
1. (![]() (f(x)dx)` = f(x). Производная от неопределенного интеграла равна подынтегральной функции.
(f(x)dx)` = f(x). Производная от неопределенного интеграла равна подынтегральной функции.
2. Дифференциал от неопределенного интеграла равен подинтегральному выражению. d(![]() f(x)dx) = f(x)dx.
f(x)dx) = f(x)dx.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.
![]() d(F(x)) = F(x) + C.
d(F(x)) = F(x) + C.
4. Постоянный множитель можно выносить за знак интеграла:
![]() , где к - число
, где к - число
5. Интеграл от суммы двух функций равен сумме интегралов от этих функций
![]() (f(x) +φ(x))dx =
(f(x) +φ(x))dx = ![]() f(x)dx +
f(x)dx + ![]() φ(x)dx.
φ(x)dx.
Для вычисления неопределенных интегралов от функций используют таблицу неопределенных интегралов, которая приводиться ниже.
Таблица неопределенных интегралов.
1. ![]() хα dx = [xα+1 / (α +1)] +C, α ≠ -1, α Є R
хα dx = [xα+1 / (α +1)] +C, α ≠ -1, α Є R
2. ![]() dx/x = ln│x│+C
dx/x = ln│x│+C
3. ![]() ax = (ax/ln a)+C,
ax = (ax/ln a)+C, ![]() exdx = ex+C
exdx = ex+C
4. ![]() sinx dx = -cosx + C
sinx dx = -cosx + C
5. ![]() cosx dx = sinx + C
cosx dx = sinx + C
6. ![]() dx/(cosx)2 = tgx + C
dx/(cosx)2 = tgx + C
7. ![]() dx/(sinx)2 = -ctgx + C
dx/(sinx)2 = -ctgx + C
8. ![]() dx /
dx /![]() 2-x2) = (arcsin x/a) + C
2-x2) = (arcsin x/a) + C
9. ![]() dx /
dx / ![]() 2 – x2) = (-arccos x/a) +C
2 – x2) = (-arccos x/a) +C
10. ![]() dx / a2 +x2 = 1/a arctg x/a +C
dx / a2 +x2 = 1/a arctg x/a +C
11. ![]() dx / a2 +x2 = - 1/a arcctg x/a +C
dx / a2 +x2 = - 1/a arcctg x/a +C
12. ![]() dx / a2 -x2 = 1/2a ln │x+a/x-a│ +C
dx / a2 -x2 = 1/2a ln │x+a/x-a│ +C
13. ![]() dx /
dx / ![]() a2 +x2) = ln │x+
a2 +x2) = ln │x+ ![]() 2+x2)│ +C.
2+x2)│ +C.
Пример 1. Вычислить ![]() (2х2 -3
(2х2 -3![]() -1)dx.
-1)dx.
Решение. Воспользуемся свойствами 4 и 5 неопределенных интегралов и первой табличной формулой. ![]() (2х2 -3
(2х2 -3![]() -1)dx = 2
-1)dx = 2![]() х2 dx - 3
х2 dx - 3![]() х1/2 dx -
х1/2 dx - ![]() dx=
dx=
= 2(x2/2) – 3[(х3/2 *2)/3] – x + C = x2 - 2![]() 3 – x +C.
3 – x +C.
Пример 2. ![]() (2/
(2/![]() -1/х + 4sinx)dx =
-1/х + 4sinx)dx = ![]() 2х –1/2dx – ln │х│ - 4cosx + C =
2х –1/2dx – ln │х│ - 4cosx + C =
= 2[(x1/2 *2)/1] – ln │x│ - 4 cosx +C = 4![]() -ln│x│- 4cosx + C.
-ln│x│- 4cosx + C.
Для вычисления неопределенных интегралов применяют следующие методы: метод непосредственного интегрирования, метод подстановки(метод замены переменной), метод интегрирования по частям.
Существуют элементарные функции первообразные которых элементарными функциями не являются. По этой причине соответствующие неопределенные интегралы называются «неберущимися» в элементарных функциях, а сами функции не интегрируемыми в элементарных функциях.
Например, ![]() e –x^2 dx,
e –x^2 dx, ![]() sinх2 dx,
sinх2 dx, ![]() cosх2 dx,
cosх2 dx, ![]() sinx/x dx,
sinx/x dx, ![]() cosx/x dx,
cosx/x dx, ![]() dx/lnx – «неберущиеся» интегралы , т.е. не существует такой элементарной функции, что F `(x) = e –x^2, F ` (x) = sinx2 и т.д.
dx/lnx – «неберущиеся» интегралы , т.е. не существует такой элементарной функции, что F `(x) = e –x^2, F ` (x) = sinx2 и т.д.
Тема 13. Определенный интеграл, его свойства.
Формула Ньютона - Лейбница.
Понятие интегральной суммы.
Пусть на отрезке [a, в] задана функция у = f(x). Разобьем отрезок на п элементарных отрезков точками деления а = х0, х1, х2, …, хп = в. На каждом элементарном отрезке [xi-1, xi] выберем произвольную точку Сi и положим
|
|
Эту сумму будем называть интегральной суммой для функции у=f(x) на отрезке [а, в]. Интегральная сумма зависит как от способа разбиения отрезка [a, в] на п частей так и от выбора точек С1, С2, …, Сп на каждом элементарном отрезке разбиения.
Геометрический смысл интегральной суммы.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Пусть у = f(x) неотрицательна на отрезке [а, в]. Рис.1
Пусть у = f(x) неотрицательна на отрезке [а, в]. Рис.1

![]() y = f(x)
y = f(x)
![]()
![]()
![]() у
у
![]()
S1 S2 S3
0 а=х0 в1 х1 с2 х2 с3 х3 =в х
Рис.1
Пусть п=3, тогда а = х0, х1, х2, х3=в.
С1 ,С2 ,С3 точки, выбранные произвольно на каждом элементарном отрезке.
S1 = f1(C1) ∆x1 – площадь прямоугольника, построенного на первом отрезке разбиения, ∆х1 = х1-х0,
S2 = f2(C2) ∆x2 – площадь прямоугольника, построенного на втором отрезке разбиения. ∆х2 = х2-х1,
|
|
Это площадь ступенчатой фигуры, составленной из прямоугольников.
Понятие определенного интеграла.
|
|
|
|
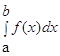 , т.е
, т.е 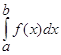 = lim Σ f(Сi)∆xi при
= lim Σ f(Сi)∆xi при max ∆xi →0
Число а называется нижним пределом, b – верхним пределом, f(x) – подинтегральной функцией, f(x)dx – подинтегральным выражением.
Некоторые свойства определенного интеграла.
10 . Значение определенного интеграла не зависит от обозначения переменной интегрирования, т.е.
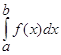 =
= 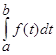 =
= 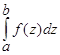 и т.д.
и т.д.
20. 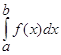 есть число.
есть число.
30. 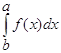 = -
= - 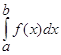 , а<b
, а<b
40. Постоянный множитель можно выносить за знак интеграла.
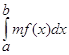 = m
= m 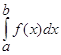 , где m – const.
, где m – const.
50. Интеграл от суммы функций равен сумме интегралов.
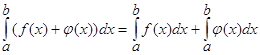
60. Если отрезок интегрирования разбит на части (a < c < b), то интеграл на всем отрезке равен сумме интегралов на каждой из частей.
|
|
|
|
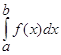 =
= 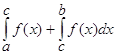 ,
, Существует еще ряд важных свойств определенного интеграла, которые подводят нас к формуле для вычисления определенного интеграла. Эта формула называется формулой Ньютона – Лейбница для f(x) непрерывной на [а; b].
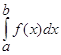 = F(b) – F(a), где F(x) некоторая первообразная для функции f(x).
= F(b) – F(a), где F(x) некоторая первообразная для функции f(x).
Например, ![]() - вычислить.
- вычислить.
1)
|
|
2) Подставим в первообразную х3/3 вначале значение верхнего предела, равного 1, затем значение нижнего предела, равного 0 вместо х.
|
|
|
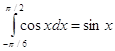 │= sin π/2 – sin π/6 = 1 – ½ = 1/2
│= sin π/2 – sin π/6 = 1 – ½ = 1/2
|
= 4 – 4 –(1- (1/4)) = -3/4.
Тема 14. Несобственные интегралы.
Мы ввели понятие определенного интеграла от функции y = f(x) на отрезке [а; b], когда функция y = f(x) была интегрируема (и, следовательно, ограничена) на конечном отрезке [а; b]. Если отрезок интегрирования бесконечен, или функция не ограничена на отрезке интегрирования, то мы встречаемся с понятием несобственного интеграла.
Несобственные интегралы с бесконечными пределами интегрирования.
Рассмотрим интеграл с переменным верхним пределом 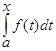 . Такой интеграл есть некоторая функция от переменного верхнего предела, т.е.
. Такой интеграл есть некоторая функция от переменного верхнего предела, т.е.
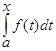 = Ф(х), х ≥ а.
= Ф(х), х ≥ а.
Определение. 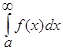 – называется несобственным интегралом от функции f(x) на интервале [а;¥), вводится он как предел функции Ф(t) при t ®¥, т.е.
– называется несобственным интегралом от функции f(x) на интервале [а;¥), вводится он как предел функции Ф(t) при t ®¥, т.е.
|
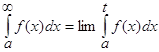 .
. Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, если предел бесконечен или не существует, то несобственный интеграл называется расходящимся.
|
|
|
|
|
|
|
|
Интеграл сходится к ½.
По аналогии определяется несобственный интеграл на интервале (-¥, b].
|
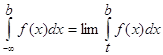
Определение сходимости 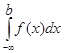 аналогично предыдущему.
аналогично предыдущему.
Вводится понятие несобственного интеграла на интервале (-¥; ¥).
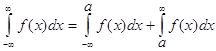 , а – некоторое число.
, а – некоторое число.
Интеграл ![]() сходится, если оба интеграла
сходится, если оба интеграла ![]() и
и 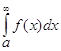 сходящиеся, если же один из них расходится, то
сходящиеся, если же один из них расходится, то ![]() - расходится.
- расходится.
Пример 3. Вычислить 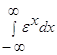 .
.
|
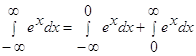 .
.
|
|
|
|
|
Этот интеграл расходится, значит ![]() - расходящийся несобственный интеграл.
- расходящийся несобственный интеграл.
В курсе теории вероятностей встречается несобственный интеграл 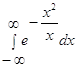 . этот интеграл называется интегралом Эйлера-Пуассона.
. этот интеграл называется интегралом Эйлера-Пуассона.
Доказано, что 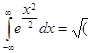 2p).
2p).
Несобственные интегралы от разрывных функций.
|
|
|
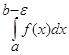 , где e > 0, то он называется несобственным интегралом от функции y = f(x) на интервале [а; b) и обозначается
, где e > 0, то он называется несобственным интегралом от функции y = f(x) на интервале [а; b) и обозначается 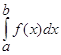 , т.е.
, т.е. 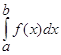 = lim
= lim 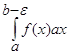
В этом случае несобственный интеграл называется сходящимся, в противном случае – расходящимся.
Аналогично вводится понятие несобственного интеграла
|
|
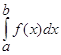 = lim
= lim 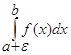 , если lim f(x) = ¥
, если lim f(x) = ¥
|
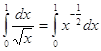 = 2х1/2 │ = 2(
= 2х1/2 │ = 2(Интеграл сходится к 2.
Тесты к теме 1.
1. На сколько периодов условно можно разделить развитие математики (по Колмогорову)?
1: 2
2: 4
3: 1
4: 5
2. К какому времени относится начало периода элементарной математики?
1-: XV в
2: I век н.э.
3: VI-V век до н.э.
4: XII в.
3. Что является предметом изучения науки “Математический анализ”?
1: функция
2: число
3: совокупность чисел
4: геометрические образы (точка, прямая, плоскость).
4. Перечислите основные черты математического мышления.
1: логические рассуждения, математическая интуиция;
2: доказательство;
3: математическая интуиция;
4: умение правильно считать.
5. Какие два вида умозаключений преобладают в математике?
1: моделирование, дедукция.
2: индукция, интуиция;
3: абстрагирование, интуиция;
4: индукция, дедукция;
6. Является ли математика искусством вычислять или наукой?
1: наука,
2: искусство вычислять.
Тесты к тема 2
1.Аксиома – составная часть дедуктивной системы. Это …?
1: Определение основных понятий данной науки.
2: Утверждение, требующее доказательства.
3: Утверждение, принимаемое без доказательств.
4: Некоторое логическое рассуждение.
2.Внутри дедуктивной системы не могут быть решены два вопроса. Какие из представленных?
1: Нужны ли доказательства аксиом? и Являются ли теоремы составной частью дедуктивного метода?
2: О смысле основных понятий. и Об истинности аксиом.
3:Можно ли определить в данной науке основные понятия? и Являюся ли доказательства составной частью дедуктивного метода?
3.Что представляет собой книга «Начала» Евклида?
1: Философское учение греческого философа и ученого Евклида.
2: Аксиоматическое построение геометрии.
3: Мифы Древней Греции.
4: Учение о параллельных прямых.
4Кто из математиков почти одновременно с Н.И. Лобачевским подошел к созданию неевклидовой геометрии?
1: Гаусс, Бойяй
2: Лагранж, Ферма
3: Пуассон, Эйлер
4: Коши, Буняковский
5.В каком году был построен Императорский Казанский Университет?
1; 1804
2: 1800
3: 1850
4: 1900.
Тесты к теме 3.
1 Что представляет собой мнимая единица ?
1: корень кв. из -1,
2: –1
3: ( i )^2
4: (-1)^2
2. Найти корни квадратного уравнения х*х-х+1=0
1: Х1=1/2; Х2=3/2
2: Корней нет
3: Х1,2=1/2+-3/2i
4: Х1=2, Х2=-1
3. Произвести действия: Если Z1=1-2i, Z2= -2+3i, Найти Z1+Z2.
1: Z=1-i
2: Z= -1+i
3: Z=2+3i
4: Z=1+2i
4. Произвести действия : Если Z1=1-2i, Z2= -2+3i, Найти Z1*Z2.
1: Z= 4
2: Z=-8+3i
3: Z= -2+6i
4: Z=4-i
5. Найти Z”, если Z=2-i.
1: Z= -2-i
2: Z= -2+i
3: Z= 2+i
4: Z= 2
6. Представить число Z = -3 в виде комплексного числа. Указать его вещественную и мнимую части.
1: Z=3-3i, Re Z=3, Im Z= -3
2: Z=-3+iо, Re Z=-3, Im Z=0
3: Z=3i, Re Z=-0, Im Z=3
4: Z=3*i*i Re Z=0, Im Z=3
7. Найти корни квадратного уравнения х^2+4=0
1: Х=2
2: Корней нет
3: Х1,2=+-2i
4: Х= -2
8. Дано комплексное число Z= -3+2i. Найти координаты точки на плоскости хоу ему соответсвующие.
1; (-3;2)
2: (3,2)
3: (3, -2)
4: (-3,0)
9. Выделить вещественную и мнимую части числа Z=1-3i/5-i.
1: Z=1/5-3i
2: Z=4/13 – 7/13i
3: Z=1/26-3i
4: Z=1-i
Тесты к теме 4.
1.Даны точки М1(3,1); М2(2,3); М3(6,0); М4(-3,-1).
Определить какая из точек лежит на прямой 2х-3у-3=0
1: М1(3,1);
2: М2(2,3);
3: М3(6,0);
4: М4(-3,-1).
2.Дана прямая х-3у+2=0, точка М(1,у) лежит на этой прямой. Найти ордин ату этой точки.
1: у=-1,
2: у=0,
3: у=1,
4: у=5.
3.Дана прямая х-3у+2=0, точка Р(х,2) лежит на этой прямой. Найти абциссу этой точки.
1: х=0,
2: х=4,
3: х=1,
4: х= -4.
4.Даны точки А(-3,2) и В(1,6). Найти расстояние между ними АВ.
1: АВ=2.
2: АВ=4,
3: АВ=8,
4: АВ=4 * корень кв. из 2,
5.Даны четыре пары, указать какие из них являются параллельными прямыми.
| 1) 2х+3у-1=0 4х+6у+1=0 | 2) х+у+5=0 х-у-3=0 | 3) х+5=0 2х+5у=0 | 4) х-2у+3=0 2х-у-1=0 |
| 1: 2х+3у-1=0 4х+6у+1=0 | ||
| 2: х+у+5=0 х-у-3=0 |
| |
| 3: х+5=0 2х+5у=0 |
| |
| 4: х-2у+3=0 2х-у-1=0 |
| |
6.Даны уравнения линий 1) у^2=х, 2)у=х^2+1, 3)х-у=0, 4)х^2 +у^2=1
Найти среди них уравнение прямой.
1: у^2=х,-
2: х - у=0,
3: у=х^2+1
4: х^2+у^2=1
7.Дано уравнение прямой у-2х+1=0. Записать это уравнение, как уравнение прямой с угловым коэффициентом. Найти отрезок в, отсекаемый прямой от оси ординат.
1: в= -1
2: в=1
3: в=1/2
4: в=0
8.Дана точка М(-1,2). Найти уравнение прямой проходящей через эту точку параллельно прямой 2х - у+3=0
1: х=2у
2: 2х - у=0;
3: х+у - 2=0;
4: 2х - у+4=0;
9.Среди заданных четырех прямых определить две перпендикулярные прямые.
1) х+у-5=0, 2)у=+х+2, 3)3х-3у+1=0, 4)2х=у
1: х+у-5=0, у=+х+2
2: х+у-5=0, 2х=у
3: у=х+2, у=2х
4: у=х+2, 3х-3у+1=0.
10.Дана прямая х+у-5=0. Найти точку А пересечения этой прямой с осью ох.
1: А(1,1);
2: А(-5,0);
3: А(5,0);
4: А(0,5)
Тесты к теме 5.
1.Написать уравнение окружности с центром в начале координат, радиусом равным 2.
1: х^2 + у^2 = 4
2: х^2 + у^2 = 2
3: (х – 2)^2 + (у – 2)^2 = 4
4: х^2 = 2
2.Х^2 + у^2 + 2х = 0. Дано уравнение окружности. Указать точку, лежащую на этой окружности: М1(0, 0), М2(1, 2), М3( - 1, 3); М4(0, 2).
1: М2(1, 2),
2: М1(0, 0),
3: М3( - 1, 3),
4: М4(0, 2),
3.Из четырех уравнений найти уравнение эллипса.
1) х/25 + у/16 = 1, 2) х^2/9 + у^2/4 = 1, 3) у^2 = 1 – х, 4) х^2 + у^2 = 9
1: нет уравнения эллипса
2: х/25 + у/16 = 1
3: х^2/9 + у^2/4 = 1
4: х^2 + у^2 = 9
4.Выделить уравнение гиперболы из четырех уравнений:
1) х/16 - у/9 = 1, 2) х^2 – у^2 = 1, 3) х^2 + у^2 = 1, 4) х^2 + 2у^2 = 1
1: х^2 + 2у^2 = 1
2: х/16 - у/9 = 1,
3: х^2 + у^2 = 1,
4: х^2 – у^2 = 1,
5.Написать уравнение эллипса, зная, что малая полуось в=3, расстояние между фокусами F1 F2= 8.
1: x^2/64+y^2/9=1
2: x^2/16+y^2/9=1
3: x^2/8+y^2/9=1
4: x^2/25+y^2/9=1
6.Написать уравнение эллипса, если большая полуось а=в, эксцентриситет Е=0,5.
1: x^2/6+y^2/2=1
2: x^2/6+y^2/9=1
3: x^2/36+y^2/27=1
4: x^2+y^2=1
7.х^2/18 – y^2/4,5=1 Дано уравнение гиперболы. Написать уравнение асимптот.
1: y=+-х
2: у=+-1/2х;
3: y=+-1/18 х
4: y=1/3х
8.На параболе у^2=6х найти точку с абциссой равной 6
1: М(0,6)
2: М(6,6)
3: М(6,0)
4: М1(6,6) и М2(6,-6)
9. Дана парабола у^2=6х. Найти координаты фокуса F.
1: F(3/2;0)
2: F(3,0)
3: F(0,6)
4: F (0,3)
10.Написать уравнение гиперболы, если а=9, в=4.
1: x/81 - y/4=1
2: x^2/9+y^2/4=1
3: x^2/81 - y^2/16=1
4: x^2 - y^2=9
Тесты к теме 6.
1. Вычислить определитель !2 3!
!4 5!
1: -2,
2: 22,
3: 2,
4: 7,
2. Вычислить определитель !2 3!
!4 5!
1:-5,
2: 10,
3: 1,
4: 0,
3. Справедливо ли равенство !2 8 10! !1 4 5!
!1 3 -1! =2 !1 3 –1! ?
!2 0 !1 !2 0 1!
1: Нет,
2: Да,
4. Дан определитель !1 5 3! Найти минор М21 к элементу а21 = 6.
!6 1 0!
!3 0 –1!.
1: М21= 0,
2: М21= -2,
3: М21= 1,
4: М21= 4,
5.Дан определитель !1 5 3! Найти алгеброическое дополнение А21 к
!6 1 0! элементу а21 = 6.
!3 0 –1!.
1: А21= 2,
2: А21= -2,
3: А21= 1,
4: А21= 4,
6. Если элементы второй строки определителя умножить на соответствующие алгебраические дополнения и произведения сложить, то получим:
1: отрицательное число,
2: ноль,
3: любое число,
4: величину определителя,
![]() 7. Дана система уравнений х+у=3
7. Дана система уравнений х+у=3
2х-3у=1.
Имеет ли эта система единственное решение?
1: Да,
2: Нет.
![]() 8. Дана система уравнений х - у=1
8. Дана система уравнений х - у=1
4х-4у=4
1: система не имеет решения,
2: система имеет единственное решение,
3: система неопределенная,
![]() 9. Дана система 2х-3у+5z=1
9. Дана система 2х-3у+5z=1
х+у-z =2
3х-у-2z=3
Указать свободные члены:
1:(5, -1, -2);
2: (2, 1, 3);
3: (-3, 1, -1);
4: (1, 2, 3);
10. Может ли определитель иметь три строки и два столбца?
1: Да.
2: Нет,
Тесты к теме 7.
1. Выберите правильное утверждение:
1) Матрица может иметь любое число строк и столбцов.
2) Матрица всегда имеет одинаковое число строк и столбцов.
3) Матрица не может состоять из одной строки.
4) Матрица не может состоять из одного столбца.
Ответ: 1)
Ответ: 2)
Ответ: 3)
Ответ: 4)
2. Может ли матрица состоять из одного элемента?
1: Да,
2: Нет,
3: Да, если это элемент не равен нулю.
3. Умножить матрицу А=(1, -1, 3, ½) на число (-2):
1: -7
2: (1, -1, 3, -1)
3: (-2, -1, 3, ½)
4: (-2, 2, -6, -1)
4. Можно ли сложить матрицы 2*2 и 3*3?
1: Нет
2: Да.
5. Можно ли перемножить матрицы соразмерности 2*3 и 3*4?
1: Нет.
2: Да.
6. Транспонирование матриц – это:
1) Перестановка местами двух столбцов.
2) изменение знака у всех элементов,
3) Перестановка местами двух строк,
4) перестановка местами строк и столбцов,
Ответ: 1)
Ответ: 2)
Ответ: 3)
Ответ: 4)
7. Если размерность исходной матрицы равна 6*7, то транспонированная матрица будет иметь размерность:
1: 6*6
2: 6*7
3: 7*6
4: 7*7
8. Единичная матрица – это:
1: Матрица, у которой все элементы равны 1.
2: Матрица, у которой элементы главной диагонали равны 1, а остальные нули
3: Матрица, определитель которой равен 1.
4: Матрица, содержащая только один элемент.
9. Если А=(1,3, -2), В= (-1)
(0 )
(2 ) , то А*В равно
1: -5
2: (-1 0 –4)
3: (-1)( 0 )(-4)
4: Перемножить нельзя
Тесты к теме 8.
1. N – множество натуральных чисел. Какое из множеств является его подмножеством: А= {2, 4, 6, 8…}, В= (N2, N3, N4,…}; С= {1, 1/2, 1/3, 1/4, …};
Д= {1, 0, 1}?
1: В,
2: А,
3: С,
4: Д,
2. Найти пересечение множеств А= {1, 3, 5, 7, 9} и В= {2, 4, 6, 8}.
Ответ: пустое множество,
1: {1}
2: {1,2,3,4,5,6,7,8}
3: {0}
3. Найти объединение множеств А и В, если А = {1,3,5,7,9}; B = {2,4,6,8}.
1: AUB = {0}
2: AUB = 0
3: АUB = {1, 2, 3, 4, 5, 6, 7, 8, 9}
4: AUB = {2,4,6,8}
4. Найти разность множеств А \ В, если А = {1,2,3,4}; B = {0,1,2}.
1: А\B = {3, 4}
2: A\B = {0,3,4}
3: A\B = {0,1,2}
4: A\B = {1,2,3}
5. Если /х/<2, то в виде двух неравенств его можно записать так:
1: -2<x<2
2: -2<=x<=2
3: 0<x<2
4: -2<x<0.
6. Если /х-1/<E, то E – окрестность точки 1 можно записать так:
1: -Е<x<Е
2: 1-Е<x<1+Е
3: 0<x<1+Е
4: -Е<x<0.
7. Если х принадлежит [-1, 3]. Какое из значений может принять х?
1: x<-1
2: -x= -3
3: x=0
4: x=4.
8. Если х не принадлежит (-2, 2). Какое из значений может принять х?
1: x= -1.
2: -x= 0
3: x=2
4: x= -4
9. Если –2<х<=0, то решением является:
1: (-2, 0)
2: (-2, 0]
3: (-2, 2)
4: [-2, 0].
10. Найти пересечение множеств (-2, 2) и (-3, 1):
1: (-3, 2)
2: [0, 1]
3: (-2, 1)
4: [-2, 0].
Тесты к теме 9. «Функция. Классификация функций».
1. Найти область определения функции у = (х-2) / (х^2 – 9)
1: (0, 2)
2: (-00, -9) U (9, 00).-
3: (2, 3).
4: (-00, -3) U (-3,3) U (3,00).
2 Найти область определения функции у = (х-1)^1/2
1: (-00, 00).
2: (0, 00).
3: [1, 00).
4: x = 0
3. Найти область определения функции у = lg(2+х)
1: (-2, 00).
2: [2, 00).
3: (-00, 00).
4: x = 0
4. Найти значения функции у = х^2/ (х-1) в точке х = 0.
1: у = -1.
2: у = 0.
3: у = 00.
4: у = 2
5. Найти значения функции у = х^2/(х-1) в точке х = 1.
1: у = -1.
2: у = 1.
3: не существует.
4: у = 2
6. Найти значения функции у = х^2/(х-1) в точке х = (а^2) +1.
1: у = не существует.
2: у = ([а^2]+1)/а^2.
3: у = -1.
4: у = [(а^2 + 1)^2]/а^2.
7. Дана функция у = (sinх)^2 +5. К какому классу функций она принадлежит?
1: Трансцендентная.
2: алгебраическая.
8. Написать целую алгебраическую функцию второй степени, в общем виде.
1: у = х^2.
2: у = [(А0)*х^2] + (А1)*х + А2.
3: у = [(А0)х^2]+1.
4: у = (х^2)/(х+1)
9. Указать дробно-рациональную функцию из заданных функций:
1) у=2*х/(1+х+х^2); 2) у=х/(sinх); 3) у=(2)^х/2; 4) у= lg(х+2)/(х-2)
Ответ: 1).
Ответ: 2).
Ответ: 3).
Ответ: 4).
10. Дана сложная функция у = [sin (1-х)]^2. Представить ее в виде цепочки простых функций.
1: U = sin x, V = U-1, y = (U-1)^2.
2: U = sin(1-x), y = U^2.
3: U = 1-х, V = sinU, y = V^2.
4 y = [sin(1-x)]^2 – простая функция
Тесты к теме 10.
|
1: 2
2: 0
3: не существует.
4: 1
|
1: не существует.
2: 0
3: 2/3
4: 1/2
|
1: 0
2: 5/6
3: 1/2
4: 1/6
|
1: 1
2: 0
3: -1
4: 00
|
1: 1
2: 0
3: не существует.
4: 00
|
1: не существует.
2: 0
3: 00
4: 5
|
1: 00
2: 1
3: е
4: не существует
|
1: е2
2: е
3: 1
4: 00
9. Является ли функция у=х2 непрерывной в точке х=2
1: Нет
2: Да
10. Является ли функция у=1/(2х+1) непрерывной в точке х=1
1: Да
2: Нет
Тесты к теме 11.
1. Найти приращение функции у=1/х, если х=1, ∆х=0,1.
1: - 1/11,
2: 0,1,
3: 0,01,
4: - 1,
2. Пользуясь определением производной, найти производную от функции у=х^3.
1: 3х^2∆х,
2: х^2,
3: 3х^2 - 1,
4: 3х^2,
3. Найти производную от функции у=хe^x , в точке х=0.
1: e+e^-1,
2: e^1,
3: 1,
4: 0,
4. Найти производную от функции у=х^5 – ¼x^4 + 3, в точке х.
1: 5x^4 – x^3 + 3,
2: 5х^4 – x^3,
3: 5x^4 – x^4 + 1,
4: 3,
5. Найти производную от функции у=sinx/cosx
1: sinx - cosx,
2:-cosx/sinx,
3: 1/cosx^2,
4: 1,
6. Найти дифференциал функции у=х^3 – 1.
1: 3(dx)^2,
2: 3x^2,
3: 3dx,
4: 3х^2dx,
7. Дана функция у=3х^2 – х + 1. Найти у``
1: 6x,
2: 6,
3: 1,
4: 6x^2,
8. Найти у```, если у=х^6 – 1/4х^4+1/2x^2+2.
1: 120х^3 – 2x,
2: 120x^3,
3: 120x^3 – 2x +2,
4: 120,
9. Найти у```, если у=(х^2)*e^x.
1: 2e^х + 4xe^x +(x^2)*e^x,
2: 2xe^x+(x^2)*e^x,
3: 2xe^x + e^x,
4: 2e^x,
Тесты к теме 12.
1. Найти первообразную для функции у = х.
1: х – 2
2: 2х,
3: 2х^2,
4: (х^2)/2.
2. Даны функции F1 (x) = sinx – 8, F2 = sinx +3. Первообразными для какой функции они являются ?
1: х,
2: cosx,
3: -cosx,
4: -х.
3. Найти производную от функции $ln(x^2 +1)dx.
1: 2х/ [(x^2) +1],
2: ln[(х^2)+1].
3: ln((х^2)+1)dx,
4: 1/((x^2)+1)
4. Найти дифференциал от функции $x arcsin2x dx.
1: x arcsin2x dx.
2: arcsin2х,
3: arcsin2x dx,
4: [arcsin2x +2x/ (1-4(x^2))^1/2]dx.
5. Вычислить $d(2^x^2)
1: (2^х^2) (ln2)2x,
2: (2^х^2)+C.
3: (2^х^2)dx,
6. Вычислить интеграл $(x^2 -3)dx.
1: [(x^3)/3x] – 3x,
2: [(х^3)/3] – 3х +С.
3: (3х^3)+C,
4: [(x^2)-3]+C
7. Справедлива ли формула $U(x) V(x)dx = $U(x)dx*$V(x)dx?
1: Нет
2: Да.
8. Можно ли вынести постоянный множитель за знак интеграла ?
1: Да.
2: Нет
9. Указать какие из интегралов является «неберущимися» $sin(x^2) dx, $lnx/x dx, $[1+ (x^1/3)] dx.
1: sin(x^2) dx.
2: $ lnx/x dх,
3: $[1+x^1/3]dx.
10. Указать какие из интегралов является «неберущимися» $(e)^-x^2 dx,
$xe^x^2, $x^2 e^-x^2 dx, $xe^-x^2 dx.
1 .$xe^-x^2 dx,
2: $ xe^x^2 dх,
3: $e^-x^2 dx
4: $[(x^2) (e^-x^2)] dx.
Тесты к теме 13.
1. Вычислить интеграл в пределах (1, 00) от функции dx/(x^2).
1: 1,
2: расходится,
3: 0,
4: -1,
2. Вычислить интеграл в пределах (0, 00) от функции e^-x dx.
1: расходится,
2: 1,
3: 0,
4: -1,
3. Вычислить интеграл в пределах (-00, 00) от функции e^-2x dx.
1: -1,
2: 0,
3: 1,
4: расходится,
4. Вычислить интеграл в пределах (0, 1) от функции dx/x.
1: 2,
2: сходится
3: расходится,
4: 0,
Тесты к теме 14.
1. Зависит ли интегральная сумма для функции у=f(x) на отрезке [а, в] от способа разбиения отрезка на 10 частей ?
1: Да,
2: Нет,
2.Зависит ли интегральная сумма для функции у=f(х) на отрезке [а, в]от выбора точек Сi на i элементарном отрезке, i = 1,2,…,п?.
1: Нет,
2: Да,
3. Можно ли записать интеграл в пределах (0, 2) от функции (sinx^2 – 3x^1/2)dx = $ в пределах от (0, 2) от функции sinx^2 dx + 3$ в пределах (0, 2) от функции х^1/2 dx ?
1: Да,
2: Нет,
4. Можно ли записать интеграл в пределах (0, 2) от функции f(x)dx = интегралу в пределах (0, 1) от функции f(x)dx + интеграл в пределах (1, 2) от функции f(x)dx.
1: Нет,
2: Да,
5. Вычислить интеграл в пределах (4, 3) от функции (x^1/2)dx.
1: 2/3,
2: 19,
3: 38/3,
4: 1,
6. Вычислить интеграл в пределах (0,П/2) от функции (sinx)dx.
1: 1/2,
2: -1,
3: 0,
4: 1,
7. Вычислить интеграл в пределах (1, 3) от функции dx/х^2.
1: -1/3,
2: 2/3,
3: 1,
4: 0,
8. Найти значение интегральной суммы для f(x) = 1 на отрезке [a, в].
1: в-а,
2: ав,
3: 1/в-а,
4: 2,
9. Верно ли равенство интеграл в пределах (0, 2) от f(x)dx.= - интеграл в пределах (2, 0) от f(x)dx ?
1: Нет.
2: Да,
.
Похожие работы
... ” дремавшие под их покровами нации: уже абсолютистские государства де-факто были национальными, хотя политическая система покоилась на феодальных династических основаниях, затемнявших новый факт европейской истории; близкородственные этнические группы совместной социально-экономической и политической, государственной жизнью сплачивались в политические нации. Революция сметя династии и систему ...
... П.Сорокин относит следующие социальные институты: армия, церковь, образовательные институты, семья, политические и профессиональные организации, средства массовой информации и т.д.Литература Беляев В.А., Филатов А.Н. Социология: Учебн. курс для вузов. Ч. 1. – Казань, 1997. –Гл. 9. Радуев В.В., Шкаратан О.И. Социальная стратификация: учебн. пособие. М., 1996. Радугин А. А., Радугин К. А. ...
... университет П. Е. Матвеев ЭТИКА. Основы хозяйственной этики Владимир 2003 Министерство образования Российской Федерации Владимирский государственный университет П.Е. Матвеев ЭТИКА. Основы хозяйственной этики Курс лекций Ч а с т ь в т о р а я Владимир 2003 ББК 87.715.4 М 33 Рецензенты:Доктор философских наук, доктор юридических наук, профессор Владимирского юридического института ...
... », «запрещено», «безразлично» и т. п. 1 Особенности других видов норм, в том числе и их структуры, рассматриваются в пар. 4 наст. главы. 1Черданцев Л.Ф. Теория государства и права. Курс лекций. Екатеринбург, 1996. С. 83-84; Общая теория права / Под ред. А.С. Пиголкина. М., 1995. С. 157-158.1Название «диспозиция» как специальное для «карательных» норм уголовного и административного права вполне ...






0 комментариев