Навигация
Проверка значимости отдельных коэффициентов регрессии
3. Проверка значимости отдельных коэффициентов регрессии
а) Найдем оценку ковариационной матрицы вектора b:
| 5,52259 | -0,08136 | -3,44878 | |
| S*(b)=S*2(XTX)–1=0,496066(XTX)–1= | -0,08136 | 0,00267 | 0,04348 |
| -3,44878 | 0,04348 | 2,21466 |
Так как на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов уравнения регрессии, то получим следующие несмещенные оценки этих дисперсий:
S*2b0=5,52259; S*2b1=0,00267; S*2b0=2,21466;
S*b0=2,35002; S*b1=0,05171; S*b2=1,48818.
Найдем оценку корреляционной матрицы вектора b. Элементы этой матрицы определяются по формуле:
rj-1l-1=cov*(bj-1,bl-1)/(S*bj-1S*bl-1),
где cov*(bj-1,bl-1) – элементы матрицы S*(b), стоящие на пересечении j-той строки и l -того столбца ( j,l =1,2,3).
Корреляционная матрица вектора b имеет вид:
| 1 | -0,66955 | -0,98614 | |
| R*(b)= | -0,66955 | 1 | 0,56504 |
| -0,98614 | 0,56504 | 1 |
Далее, для проверки значимости отдельных коэффициентов регрессии, т.е. гипотез H0: m=0 (m=1,2), по таблицам t-распределения для =0,05, =7 находим tкр=2,365. Вычисляем tнабл для каждого из коэффициентов регрессии по формуле tнабл(bj)=bj/S*bj:
tнабл(b1)=b1/S*b1=0,71892/0,05171=13,903
tнабл(b2)=b2/S*b2=1,51303/1,48818=1,01667.
Так как tнабл(b1) > tкр (13,903 > 2,365), tнабл(b2) < tкр(1,01667< 2,365), то коэффициент регрессии 10, а коэффициент регрессии 2=0. Следовательно переходим к алгоритму пошагового регрессионного анализа.
4. Пошаговый регрессионный анализ
Будем рассматривать оценку нового уравнения регрессии вида
y*=b’0+b’1x1. Вектор оценок b’ определим по формуле b=(XTX)–1XTY, где
| n | xi1 | 10 | 75 | ||
| XTX = | xi1 | x2i1 | = | 75 | 835 |
| yi | 61,4 | b’0 | 0,52534 | ||||
| XTY = | xiyi | = | 664,5 | b = | b’1 | = | 0,74861 |
Таким образом, оценка уравнения регрессии примет вид:
y*=0,52534+0,74861x1.
Повторив далее вычисления по пп 2 и 3, определяем, что новая оценка уравнения регрессии и его коэффициент значимы при =0,05.
5. Нахождение матрицы парных коэффициентов корреляции
(на примере без исключения переменной)
а) находим вектор средних:
Xср=(x1ср; x2ср; yср)=(7,5; 1,41; 6,14);
б) находим вектор среднеквадратических отклонений S=(s1; s2; sy) по формуле sj=([(xij - xjср)2]/n)0,5, i=1…n:
S=(5,22; 0,18; 3,91);
в) формируем корреляционную матрицу
| 1 | r12 | r1y | |
| R= | r21 | 1 | r2y |
| ry1 | ry2 | 1 |
где r12=r21=[(x1x2)ср-x1срx2ср]/(s1s2), ryj=rjy=[(xjy)ср-xjсрyср]/(sjsy):
| 1 | -0,565 | 0,997 | |
| R= | -0,565 | 1 | -0,612 |
| 0,997 | -0,612 | 1 |
Похожие работы
... -педагогическая или научно-техническая проблема, являющаяся новым научным вкладом в теорию определенной области знаний (педагогику, технику и другие). 4. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ БАКАЛАВРА ФИЗИКО-МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ПРОФИЛЬ ИНФОРМАТИКА 4.1. Положение о выпускной квалификационной работе бакалавра физико-математического образования: ...
... посредством организации конкурсов бизнес-идей, мини-олимпиад, работы творческих групп и пр. С целью их проведения в исследовании разработан сборник экономических задач, основанный на предложенном подходе к интеграции математического и экономического содержания, рассмотрена технология организации такого типа мероприятий. Трудности применения математических методов в экономике Трудности ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
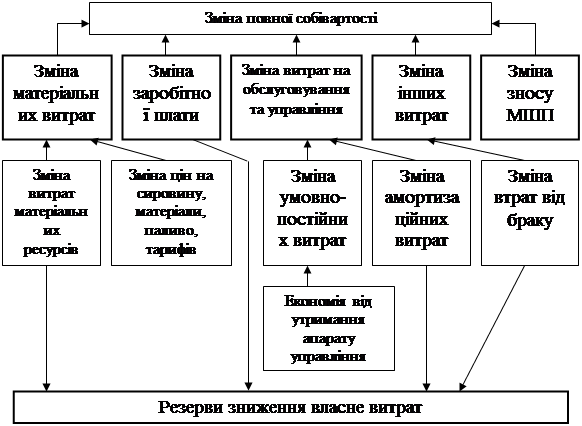
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...

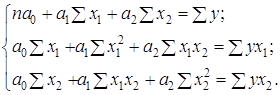
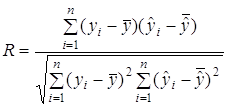
0 комментариев