Навигация
Расчет оценок частных коэффициентов корреляции
6. Расчет оценок частных коэффициентов корреляции
Оценки частных коэффициентов корреляции определяются по формулам:
r12/y=(r12-r1yr2y)/[(1-r1y2)(1-r2y2)]0,5 =0,738;
r1y/2=(r1y-r12ry2)/[(1-r122)(1-ry22)]0,5 =0,998;
r2y/1=(r1y-r12ry2)/[(1-r122)(1-ry22)]0,5 =-0,762.
Составим матрицу частных коэффициентов корреляции:
| 1 | 0,738 | 0,998 |
| 0,738 | 1 | –0,762 |
| 0,998 | –0,762 | 1 |
Следует иметь в виду, что частный коэффициент корреляции может резко отличаться от соответствующего парного коэффициента и даже иметь противоположный знак. Любой из частных коэффициентов может быть равен нулю, в то время, как парный – отличен от нуля.
В данном примере r12/y=0,738, а r12=-0,565. Такое различие вызвано тесной связью объема валовой продукции (x1) и себестоимостью товарной продукции (y): r1y=0,997. В случае независимости величин частный и парный коэффициенты корреляции равны нулю.
7. Проверка значимости парных и частных
коэффициентов корреляции
Проверка осуществляется с помощью таблиц t-распределения Стьюдента.
Для r12: tнабл=(10-2)0,5(-0,565)/(1-(-0,565)2)0,5=1,93683tкр(8;0,1)=1,86).
Для r2y: tнабл=(10-2)0,5(-0,612)/(1-(-0,612)2)0,5=2,20621 tкр(8;0,1)=1,86).
Для r1y: tнабл=(10-2)0,50,997/(1-0,9972)0,5=36,43263>tкр(8;0,05)=2,306; гипотеза H0: 1y=0 отвергается с вероятностью ошибки 0,05.
Для r12/y: tнабл=(n-3)0,50,738/(1-0,7382)0,5=2,893542>tкр(7;0,05)=2,365; гипотеза H0: 12/y=0 отвергается с вероятностью ошибки 0,05.
Для r1y/2: tнабл=(n-3)0,50,998/(1-0,9982)0,5=41,77023>tкр(7;0,05)=2,365; гипотеза H0: 1y/2=0 отвергается с вероятностью ошибки 0,05.
Для r2y/1: tнабл=(n-3)0,5(-0,762)/(1-(-0,762)2)0,5=3,11324>tкр(7;0,05)=2,365; гипотеза H0: 2y/1=0 отвергается с вероятностью ошибки 0,05.
8. Расчет оценок множественных коэффициентов
корреляции и детерминации
Оценки множественных коэффициентов корреляции детерминации рассчитываются по формулам:
ry/12 = (ry12+ ry22+ 2ry1ry2r12)/(1-r122)(1-ry22)]0,5 =0,999;
ry/122=0,9992=0,997.
9. Проверка значимости множественных коэффициентов
корреляции и детерминации
Проверим гипотезу H0: 2y/12 =0 по F-критерию. Наблюдаемое значение находится по формуле:
Fнабл= [r2y/12/(k-1)]/[(1-ry/12)/(n-k)]=[0,997/(3-1)]/[(1-0,997)/(10-3)]=1163.
По таблице F-распределения для =0,05, 1=k-1=2, 2=n-k=7 находим Fкр=4,74. Так как Fнабл>Fкр, то гипотеза о равенстве 2y/12 =0 отвергается.
Аналогично осуществляется проверка гипотезы y/12=0 (в данном примере опущено).
Тем самым доказана значимость множественного коэффициента корреляции, что говорит о наличии зависимости y от x1 и x2, т.е. себестоимость действительно зависит от объема валовой продукции и производительности труда.
Литература к задаче 1
Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Исследование зависимостей.–М.:Финансы и статистика, 1985
Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Основы моделирования и первичной обработки данных.–М.:Финансы и статистика, 1983
Львовский Е.Н. Статистические методы построения эмпирических формул.–М.:Высш.шк., 1988.
Шепелев И.Г. Математические методы и модели управления в строительстве.–М.:Высшая школа, 1980.
Задача 2
Динамическое программирование
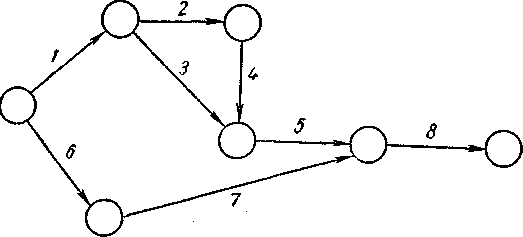
Для увеличения объемов выпуска пользующейся повышенным спросом продукции, изготавливаемой тремя предприятиями, выделены капитальные вложения в объеме 700 млн.руб. Использование i-тым предприятием xi млн. руб. из указанных средств обеспечивает прирост выпуска продукции, определяемый значением нелинейной функции fi(xi).
Найти распределение капитальных вложений между предприятиями, обеспечивающее максимальное увеличение выпус6ка продукции.
Исходные данные приведены в таблицах 5 и 6.
Таблица 5Исходные данные
| Объем кап.вложений xi, млн.руб. | Прирост выпуска продукции fi(xi), млн.руб. | ||
| Предприятие 1 | Предприятие 2 | Предприятие 3 | |
| 0 | 0 | 0 | 0 |
| 100 | а | 50 | 40 |
| 200 | 50 | 80 | d |
| 300 | b | 90 | 110 |
| 400 | 110 | 150 | 120 |
| 500 | 170 | с | 180 |
| 600 | 180 | 210 | 220 |
| 700 | 210 | 220 | 240 |
Таблица 6
Варианты исходных данных
| Вариант | a | b | c | d |
| 1 | 30 | 90 | 190 | 50 |
| 2 | 20 | 80 | 160 | 70 |
| 3 | 35 | 100 | 190 | 60 |
| 4 | 40 | 110 | 180 | 90 |
| 5 | 30 | 100 | 190 | 60 |
Окончание табл. 6
| Вариант | a | b | c | d |
| 6 | 35 | 80 | 160 | 70 |
| 7 | 40 | 80 | 160 | 70 |
| 8 | 40 | 100 | 190 | 60 |
| 9 | 30 | 110 | 160 | 90 |
| 10 | 40 | 110 | 190 | 90 |
| 11 | 20 | 100 | 190 | 60 |
| 12 | 20 | 80 | 180 | 60 |
| 13 | 35 | 110 | 190 | 50 |
| 14 | 40 | 90 | 160 | 50 |
| 15 | 30 | 90 | 190 | 90 |
| 16 | 35 | 90 | 160 | 70 |
| 17 | 40 | 90 | 190 | 50 |
| 18 | 20 | 90 | 150 | 90 |
| 19 | 20 | 80 | 190 | 60 |
| 20 | 20 | 110 | 160 | 70 |
| 21 | 40 | 90 | 190 | 60 |
| 22 | 30 | 110 | 190 | 55 |
| 23 | 35 | 90 | 180 | 70 |
| 24 | 45 | 85 | 170 | 90 |
| 25 | 40 | 85 | 170 | 50 |
В задаче необходимо:
Похожие работы
... -педагогическая или научно-техническая проблема, являющаяся новым научным вкладом в теорию определенной области знаний (педагогику, технику и другие). 4. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ БАКАЛАВРА ФИЗИКО-МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ПРОФИЛЬ ИНФОРМАТИКА 4.1. Положение о выпускной квалификационной работе бакалавра физико-математического образования: ...
... посредством организации конкурсов бизнес-идей, мини-олимпиад, работы творческих групп и пр. С целью их проведения в исследовании разработан сборник экономических задач, основанный на предложенном подходе к интеграции математического и экономического содержания, рассмотрена технология организации такого типа мероприятий. Трудности применения математических методов в экономике Трудности ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
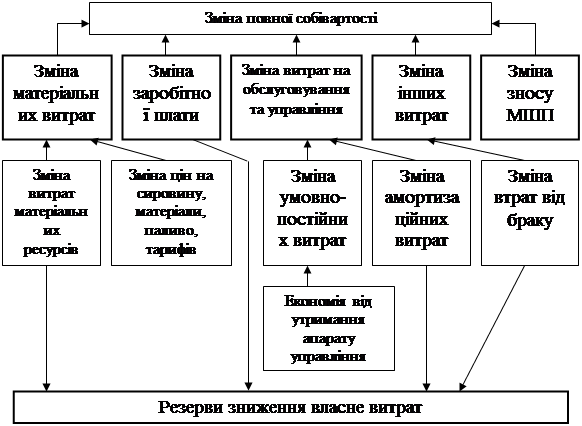
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...

0 комментариев