Навигация
Составить рекуррентное соотношение Беллмана в виде функциональных уравнений
1. Составить рекуррентное соотношение Беллмана в виде функциональных уравнений.
2. Используя рекуррентные соотношения и исходные данные определить сначала условно оптимальные, а затем оптимальные распределения капиталовложений между предприятиями.
Методические указания к решению задачи 2
Принцип оптимальности. Каково бы ни было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выйгрыш на данном шаге плюс оптимальный выйгрыш на всех последующих шагах был максимальным.
Общая последовательность решения задач динамического программирования следующая.
Выбрать способ описания процесса, т.е. параметры, характеризующие состояние системы, фазовое пространство и способ членения операции на шаги.
Записать выигрыш wi на i-том шаге в зависимости от состояния системы S в начале этого шага и управления Ui:
wi= wi(S, Ui)
Записать для i-того шага функцию выражающую изменение состояния системы от S к S’ под влиянием управления Ui:
S’=(S, Ui).
Записать основное функциональное уравнение, выражающее функцию Wi(S) через Wi+1(S):
Wi(S)=maxUi{wi(S, Ui)+Wi+1(i(S, Ui))}
Найти функцию Wm(S)=maxUm{wm(S, Um)} – условный оптимальный выйгрыш для последнего шага (максимум берется только по тем направлениям, которые приводят систему в заданную область конечных состояний S*w ) и соответствующее ей условное оптимальное управление на последнем шаге Um(S).
Зная Wm(S) и пользуясь уравнением из п.4, при конкретном виде функций wi(S, Ui), i(S, Ui), найти одну за другой функции:
Wm-1(S), Wm-2(S), … , W1(S)
и соответствующие им условные оптимальные управления:
Um-1(S), Um-2(S), … , U1(S).
Если начальное состояние системы S0 задано, то найти оптимаьный выйгрыш Wmax(S0), и далее безусловные оптимальные управления (и, при необходимости, конечное состояние системы) по цепочке:
S0U1(S0)S*1 U2(S*1)S*2 U3(S*2)…S*m-1 Um(S*m-1)S*m.
Если начальное состояние S0 не задано, а ограничено условием S0S0, тонайти оптимальное начальное состояние, при котором выйгрыш достигнет максимума и далее по цепочке, безусловные оптимальные управления.
В данной задаче вместо того, чтобы рассматривать допустимые варианты распределения капиталовложений между n предприятиями и оценивать их эффективность, необходимо исследовать эффективность вложения средств на одном предприятии, на двух предприятиях и т.д., наконец, на n предприятиях. Таким образом получим n этапов, на каждом из которых состояние системы (3 предприятия) описывается объемом средств, подлежащих освоению k предприятиями (k=1n). Управлениями будут являться решения об объемах капиталовложений, выделяемых k-тому предприятию.
Литература к задаче 2
Вентцель Е.С. Исследование операций: задачи, принципы, методология.– М.:Наука. Гл. ред. физ.-мат. лит.,1988.
Вентцель Е.С. Основы исследования операций.– М.: Советское радио, 1972.
Габасов Р.Ф., Кириллова Ф.М. Основы динамического программирования.– Минск:Изд-во БГУ,1975.
Исследование операций в экономике: Учеб. пособие для вузов по экон. специальностям / Под ред. Н.Ш.Кремера.– М.: Банки и биржи,1997.
Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах.– М.: Высшая школа,1979.
Задача 3
Марковские случайные процессы
Исходные данные задачи.
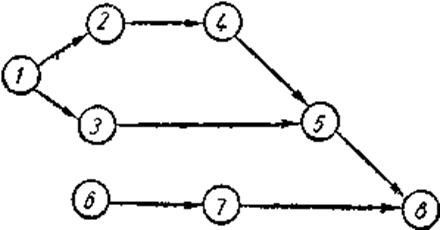
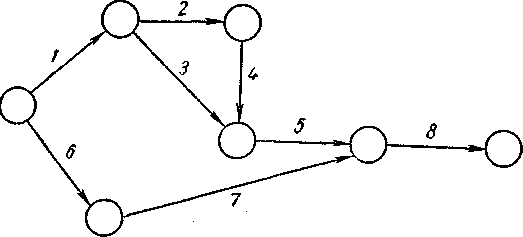
Р
азмеченный
граф состояний
системы представлен
на рис. 1.
Заданы следующие состояния системы.
S1 – исправна, функционирует (загружена).
S2 – исправна, не функционирует (не загружена).
S3 – неисправна, факт неисправности устанавливается.
S4 – факт неисправности установлен, ведется поиск неисправности.
S5 – ремонтируется.
S6 – ведется профилактический осмотр.
S7 – ведется профилактический ремонт.
Обозначение исходных данных для расчета интенсивностей потоков событий приведено в таблице 7.
Таблица 7Обозначение исходных данных
| Наименование | Обозначение | Размерность |
| Среднее время наработки на отказ | T1 | сутки |
| Среднее время функционирования системы | T2 | часы |
| Среднее время простоя исправной системы | T3 | часы |
| Среднее время установление факта неисправности | T4 | часы |
| Среднее время поиска неисправности | T5 | часы |
| Среднее время устранения неисправности (ремонта) | T6 | часы |
| Периодичность профилактического осмотра | Один раз в T7 дней | сутки |
| Средняя продолжительность проф. осмотра | T8 | часы |
| Средняя продолжительность проф. ремонта | T9 | часы |
В задаче требуется определить следующее. Окупит ли себя увеличение дохода, связанное с уменьшением Ti в nj раз (n1=2; n2=3), если при этом возникают дополнительные затраты в размере 0,5n1Di, и 0,75n2Di, где Di – убыток, приносимый системой в соответствующем времени Ti состоянии.
Варианты исходных данных приведены в табл. 8.
Таблица 8
Варианты исходных данных
№ | Значения Ti | Доход Di в единицу времени в зависимости от состояния системы (руб.) | |||||||||||||||
| вар. | Т1 | Т2 | Т3 | Т4 | Т5 | Т6 | Т7 | Т8 | Т9 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | Тi |
| 1 | 20 | 6 | 0,3 | 0,4 | 0,9 | 1,3 | 22 | 0,6 | 6 | 207 | -23 | -5 | -4 | -23 | -8 | -9 | 3 |
| 2 | 23 | 4 | 0,4 | 0,2 | 0,6 | 1,7 | 38 | 0,9 | 6 | 229 | -24 | -6 | -3 | -15 | -11 | -11 | 7 |
| 3 | 24 | 8 | 0,3 | 0,4 | 0,9 | 1 | 22 | 0,9 | 7 | 207 | -21 | -5 | -2 | -23 | -7 | -9 | 7 |
| 4 | 20 | 4 | 0,3 | 0,3 | 0,6 | 1,3 | 35 | 1 | 7 | 247 | -20 | -4 | -7 | -22 | -7 | -8 | 3 |
| 5 | 20 | 4 | 0,1 | 0,6 | 0,9 | 2,1 | 32 | 0,6 | 6 | 208 | -20 | -6 | -6 | -17 | -11 | -8 | 3 |
| 6 | 21 | 4 | 0,4 | 0,5 | 0,7 | 1,2 | 44 | 0,8 | 6 | 297 | -22 | -2 | -6 | -10 | -7 | -9 | 3 |
| 7 | 20 | 4 | 0,3 | 0,5 | 0,6 | 2 | 23 | 0,5 | 5 | 228 | -19 | -3 | -4 | -21 | -7 | -8 | 7 |
| 8 | 18 | 4 | 0,4 | 0,2 | 0,6 | 0,9 | 24 | 0,9 | 6 | 214 | -24 | -2 | -7 | -25 | -9 | -9 | 7 |
| 9 | 19 | 5 | 0,1 | 0,3 | 0,7 | 1 | 42 | 0,9 | 5 | 280 | -21 | -6 | -7 | -15 | -9 | -9 | 7 |
| 10 | 21 | 8 | 0,1 | 0,6 | 0,5 | 1,5 | 40 | 1 | 7 | 226 | -20 | -6 | -3 | -18 | -9 | -11 | 3 |
| 11 | 18 | 8 | 0,2 | 0,6 | 1 | 0,8 | 48 | 0,8 | 6 | 214 | -20 | -6 | -7 | -16 | -8 | -8 | 7 |
| 12 | 21 | 4 | 0,2 | 0,6 | 1 | 0,9 | 32 | 0,8 | 5 | 277 | -23 | -5 | -4 | -13 | -7 | -10 | 3 |
| 13 | 21 | 4 | 0,4 | 0,5 | 0,6 | 2,2 | 46 | 0,7 | 6 | 295 | -23 | -4 | -2 | -11 | -10 | -10 | 7 |
| 14 | 18 | 4 | 0,1 | 0,3 | 0,8 | 0,8 | 20 | 0,6 | 5 | 264 | -22 | -6 | -4 | -24 | -8 | -8 | 7 |
Окончание табл. 8
№ | Значения Ti | Доход Di в единицу времени в зависимости от состояния системы (руб.) | |||||||||||||||
| вар. | Т1 | Т2 | Т3 | Т4 | Т5 | Т6 | Т7 | Т8 | Т9 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | Тi |
| 15 | 19 | 6 | 0,4 | 0,3 | 0,9 | 2,1 | 29 | 0,9 | 7 | 208 | -20 | -5 | -3 | -17 | -10 | -10 | 7 |
| 16 | 22 | 4 | 0,3 | 0,2 | 0,5 | 0,9 | 35 | 0,8 | 5 | 255 | -24 | -4 | -7 | -22 | -8 | -9 | 3 |
| 17 | 18 | 8 | 0,4 | 0,5 | 1 | 0,8 | 33 | 0,5 | 7 | 207 | -21 | -2 | -4 | -15 | -10 | -11 | 3 |
| 18 | 20 | 5 | 0,4 | 0,5 | 1 | 1,9 | 22 | 0,6 | 5 | 207 | -21 | -5 | -4 | -25 | -8 | -9 | 7 |
| 19 | 21 | 5 | 0,1 | 0,6 | 0,9 | 1,3 | 40 | 0,9 | 5 | 235 | -18 | -2 | -3 | -11 | -10 | -11 | 3 |
| 20 | 18 | 5 | 0,2 | 0,3 | 0,8 | 1,2 | 43 | 0,5 | 6 | 293 | -23 | -2 | -5 | -21 | -7 | -11 | 7 |
| 21 | 25 | 4 | 0,2 | 0,2 | 0,6 | 1,2 | 45 | 0,7 | 7 | 277 | -19 | -5 | -4 | -13 | -11 | -10 | 3 |
| 22 | 18 | 5 | 0,2 | 0,5 | 0,8 | 1 | 34 | 0,8 | 6 | 210 | -21 | -6 | -5 | -20 | -9 | -11 | 3 |
| 23 | 19 | 8 | 0,3 | 0,6 | 0,8 | 2 | 33 | 1 | 6 | 232 | -25 | -2 | -3 | -14 | -11 | -12 | 7 |
| 24 | 22 | 8 | 0,1 | 0,3 | 1 | 1,9 | 29 | 0,9 | 7 | 238 | -24 | -2 | -2 | -21 | -10 | -10 | 3 |
| 25 | 24 | 5 | 0,1 | 0,6 | 0,5 | 0,8 | 41 | 1 | 7 | 266 | -22 | -5 | -4 | -15 | -11 | -12 | 7 |
Методические указания к решению задачи 3
Расчитываются интенсивности потоков событий.
Составляются уравнения Колмогорова.
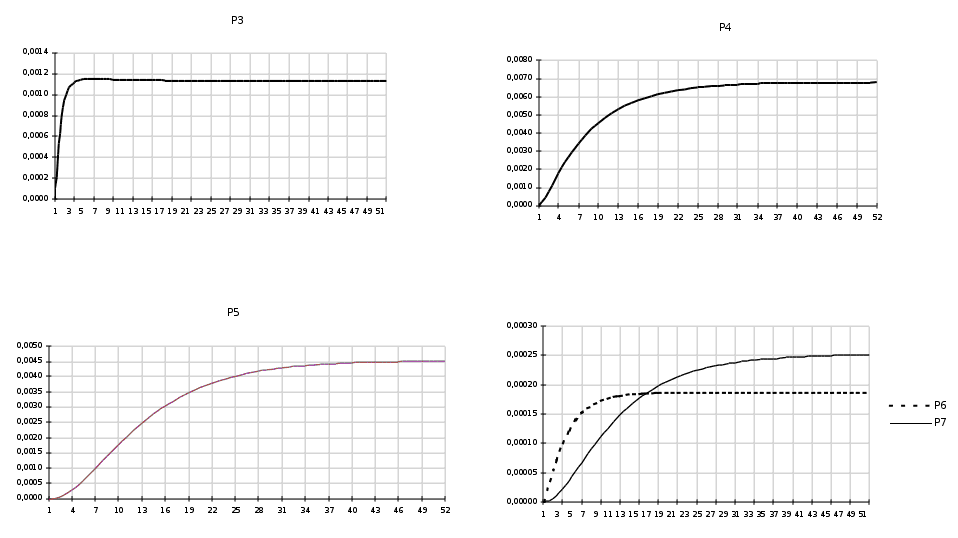
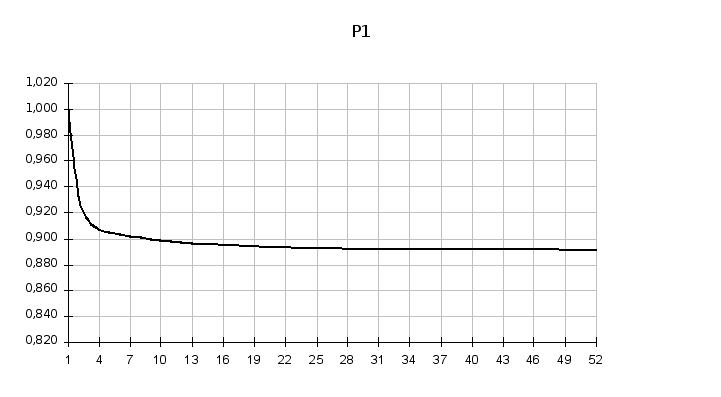
Находится решение уравнений Колмогорова (вручную и численно).
Вычисляются финальные вероятности состояний системы.
Используя значения финальных вероятностей состояний определяется доход, приносимый системой в единицу времени.
Определяется изменение дохода при уменьшении Ti. Для этого пересчитывается интенсивность соответствующенго потока событий, находится новое решение уравнений Колмогорова и новые финальные вероятности. После этого определяется новое значение дохода, определяется его разница с предыдущим и результат сопоставляется с произведенными дополнительными затратами.
Численное решение уравнений Колмогорова производится в среде MS EXCEL. Текст программы на языке VB для EXCEL приведен в приложении 2. Оформление рабочего листа – в приложении 3.
Литература к задаче 3
Вентцель Е.С. Исследование операций: задачи, принципы, методология.–М.:Наука. Гл. ред. физ.-мат. лит.,1988.
Вентцель Е.С. Основы исследования операций.– М.: Советское радио, 1972.
Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения.– М.: Наука, 1991.
Ярлыков М.С., Миронов М.А. Марковская теория оценивания случайных процессов.-М.:Радио и связь, 1993.
Задача 4
Метод Монте-Карло
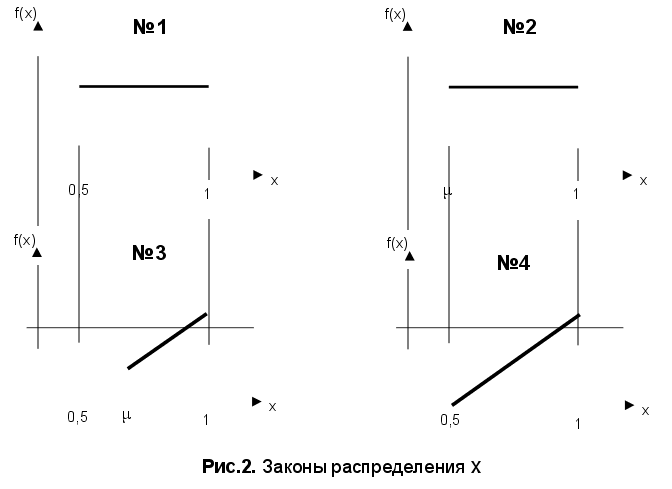
Рассчитать нетто-ставку тарифа при страховании строительства здания по исходным данным, приведенным в табл.9, табл.10. и на рис.2.
Таблица 9Обозначения исходных данных
| Наименование | Обозначение | |||
| Заданная точность | | |||
| Вероятность попадания при испытаниях в зону, ограниченную заданной точностью | | |||
| Показатель качества проектирования | п | |||
| Закон распределения xп | fп | |||
| Показатель предполагаемого качества материалов | м | |||
| Закон распределения xм | fм | |||
| Показатель предполагаемого качества выполнения СМР | с | |||
| Закон распределения xс | fс | |||
| Число этажей объекта | m | |||
| Число несущих конструкций на этаже | n | |||
| Число несущих конструкций на нулевом цикле | v | |||
| Класс подверженности внешним факторам риска | K | |||
| Вероятность внешнего фактора 1 | P1 | |||
| Вероятность внешнего фактора 2 | P2 | |||
| Вероятность внешнего фактора 3 | P3 | |||
| № | | | п | fп | м | fм | с | fс | m | n | v | K | P1 | P2 | P3 |
| 1 | 0,001 | 0,9999 | 0,85 | 2 | 0,89 | 3 | 0,80 | 2 | 6 | 6 | 6 | 4 | 6,2E-04 | 6,0E-05 | 1,3E-06 |
| 2 | 0,001 | 0,999 | 0,92 | 3 | - | 4 | - | 4 | 9 | 3 | 7 | 1 | 5,6E-04 | 2,8E-05 | 1,7E-06 |
| 3 | 0,001 | 0,99999 | 0,88 | 1 | 0,87 | 2 | 0,82 | 3 | 16 | 3 | 7 | 4 | 0 | 3,0E-05 | 6,9E-06 |
| 4 | 0,0015 | 0,99999 | - | 4 | 0,82 | 3 | 0,90 | 2 | 24 | 5 | 4 | 2 | 6,0E-04 | 3,2E-05 | 8,7E-06 |
| 5 | 0,0015 | 0,9999 | - | 4 | 0,81 | 3 | 0,90 | 3 | 48 | 5 | 4 | 5 | 7,6E-04 | 0 | 3,4E-06 |
| 6 | 0,0015 | 0,9998 | 0,90 | 1 | 0,90 | 2 | - | 4 | 9 | 5 | 8 | 3 | 7,9E-04 | 3,8E-05 | 6,9E-06 |
| 7 | 0,001 | 0,9999 | 0,83 | 3 | 0,82 | 2 | 0,68 | 2 | 6 | 2 | 5 | 4 | 6,0E-04 | 7,2E-05 | 5,6E-06 |
| 8 | 0,0018 | 0,9999 | 0,87 | 1 | 0,82 | 1 | 0,68 | 1 | 48 | 8 | 8 | 1 | 5,3E-04 | 2,1E-05 | 4,2E-06 |
| 9 | 0,0015 | 0,9998 | 0,85 | 3 | 0,83 | 2 | 0,75 | 1 | 22 | 8 | 4 | 2 | 8,2E-04 | 3,3E-05 | 5,8E-06 |
| 10 | 0,001 | 0,9998 | 0,86 | 2 | 0,86 | 3 | - | 4 | 9 | 3 | 8 | 3 | 0 | 6,0E-05 | 3,0E-06 |
| 11 | 0,0015 | 0,9999 | 0,78 | 3 | 0,88 | 3 | 0,89 | 1 | 10 | 3 | 5 | 2 | 7,3E-04 | 5,4E-05 | 3,5E-06 |
| 12 | 0,0015 | 0,9999 | 0,84 | 1 | - | 4 | 0,87 | 1 | 6 | 7 | 4 | 5 | 7,8E-04 | 3,3E-05 | 2,3E-06 |
Окончание табл. 10
| № | | | п | fп | м | fм | с | fс | m | n | v | K | P1 | P2 | P3 |
| 13 | 0,0015 | 0,9998 | 0,80 | 3 | 0,80 | 3 | - | 4 | 9 | 8 | 6 | 1 | 6,9E-04 | 3,4E-05 | 7,2E-06 |
| 14 | 0,001 | 0,9998 | - | 4 | 0,88 | 3 | 0,83 | 1 | 16 | 5 | 7 | 5 | 5,4E-04 | 5,5E-05 | 2,3E-06 |
| 15 | 0,0015 | 0,9998 | 0,73 | 2 | 0,81 | 1 | 0,82 | 3 | 24 | 2 | 5 | 5 | 7,0E-04 | 4,2E-05 | 4,5E-06 |
| 16 | 0,0012 | 0,9999 | 0,88 | 3 | 0,79 | 3 | - | 4 | 48 | 2 | 7 | 3 | 6,9E-04 | 0 | 8,3E-06 |
| 17 | 0,0015 | 0,9998 | 0,87 | 2 | - | 4 | 0,87 | 2 | 9 | 7 | 6 | 3 | 7,0E-04 | 7,2E-08 | 7,9E-06 |
| 18 | 0,001 | 0,9996 | 0,73 | 3 | 0,91 | 2 | 0,76 | 2 | 6 | 2 | 4 | 2 | 5,2E-04 | 7,4E-05 | 2,9E-06 |
| 19 | 0,0015 | 0,999 | 0,84 | 3 | 0,87 | 3 | 0,75 | 2 | 48 | 8 | 6 | 5 | 5,2E-04 | 7,2E-05 | 1,7E-06 |
| 20 | 0,0018 | 0,9997 | 0,73 | 2 | 0,92 | 1 | 0,79 | 2 | 22 | 3 | 7 | 5 | 7,8E-04 | 3,8E-05 | 6,6E-06 |
| 21 | 0,0015 | 0,9997 | - | 4 | 0,89 | 2 | 0,73 | 1 | 9 | 6 | 4 | 3 | 5,9E-04 | 3,4E-05 | 4,8E-06 |
| 22 | 0,001 | 0,999 | - | 4 | 0,92 | 1 | - | 4 | 10 | 6 | 8 | 4 | 8,1E-04 | 8,0E-05 | 4,2E-06 |
| 23 | 0,001 | 0,9998 | 0,82 | 3 | 0,87 | 1 | 0,72 | 1 | 24 | 2 | 7 | 1 | 7,2E-03 | 4,7E-03 | 5,5E-05 |
| 24 | 0,001 | 0,999 | 0,80 | 2 | 0,80 | 2 | - | 4 | 6 | 4 | 8 | 1 | 6,6E-04 | 5,5E-05 | 2,6E-06 |
| 25 | 0,001 | 0,999 | - | 4 | 0,88 | 2 | 0,84 | 2 | 9 | 8 | 8 | 2 | 5,1E-04 | 0 | 8,0E-06 |
Методические указания к решению задачи 4
Значение нетто-ставки страхового тарифа определяется по формуле
N=PAPi, i=1,2,3, (1)
где PA – условная вероятность нелокальных разрушений объекта страхования при наличии внешнего, провоцирующего аварию, фактора риска; Pi – вероятности внешних факторов.
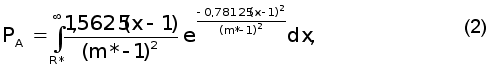
Значение
PA
вычисляется
по формуле
где R* – допустимый (нормативный) риск аварии, рассчитываемый по формуле
R*=(1+mkn/q)kv/q; (3)
k – коэффициент, зависящий от класса подверженности страхуемого объекта внешним факторам риска; q – количество последовательно возводимых несущих конструкций на нулевом цикле и типовом этаже (ярусе) объекта строительства; m – число этажей возводимого объекта; n – число несущих конструкций на этаже; v – число несущих конструкций на нулевом цикле; m* – математическое ожидание относительного риска аварии R.
Расчет m*. Зависимость R от фактических уровней надежности р возведенных несущих конструкций выражается формулой
R=(1+mр–n)р–v. (4)
Прогноз значений р до начала строительства осуществляется по формуле: р = xмxсxп+0,8(1-xм)xсxп+0,5xм(1-xс)xп+0,9xмxс(1-xп)+0,4(1-xм)(1-xс)xп+ +0,72(1-xм)xс(1-xп)+0,45(1-xс)xм(1-xп)+0,36(1-xм)(1-xс)(1-xп), (5) где xп, xм, xс – случайные величины с законами распределения fп, fм и fс соответственно.Применяя далее процедуру метода Монте-Карло, по выражениям (4) и (5) строится статистический ряд значений R в интервале от 1 до . Для этого для равномерно распределенных случайных чисел i в интервале [0,1], разыгрываются случайные величины xп, xм, xс на соответствующих заданию интервалах. Метод перехода от i к xi следующий. Зная закон распределения f(x) (f(xп)=fп, f(xм)=fм, f(xс)=fс) и выработав , необходимо взять определенный интеграл
и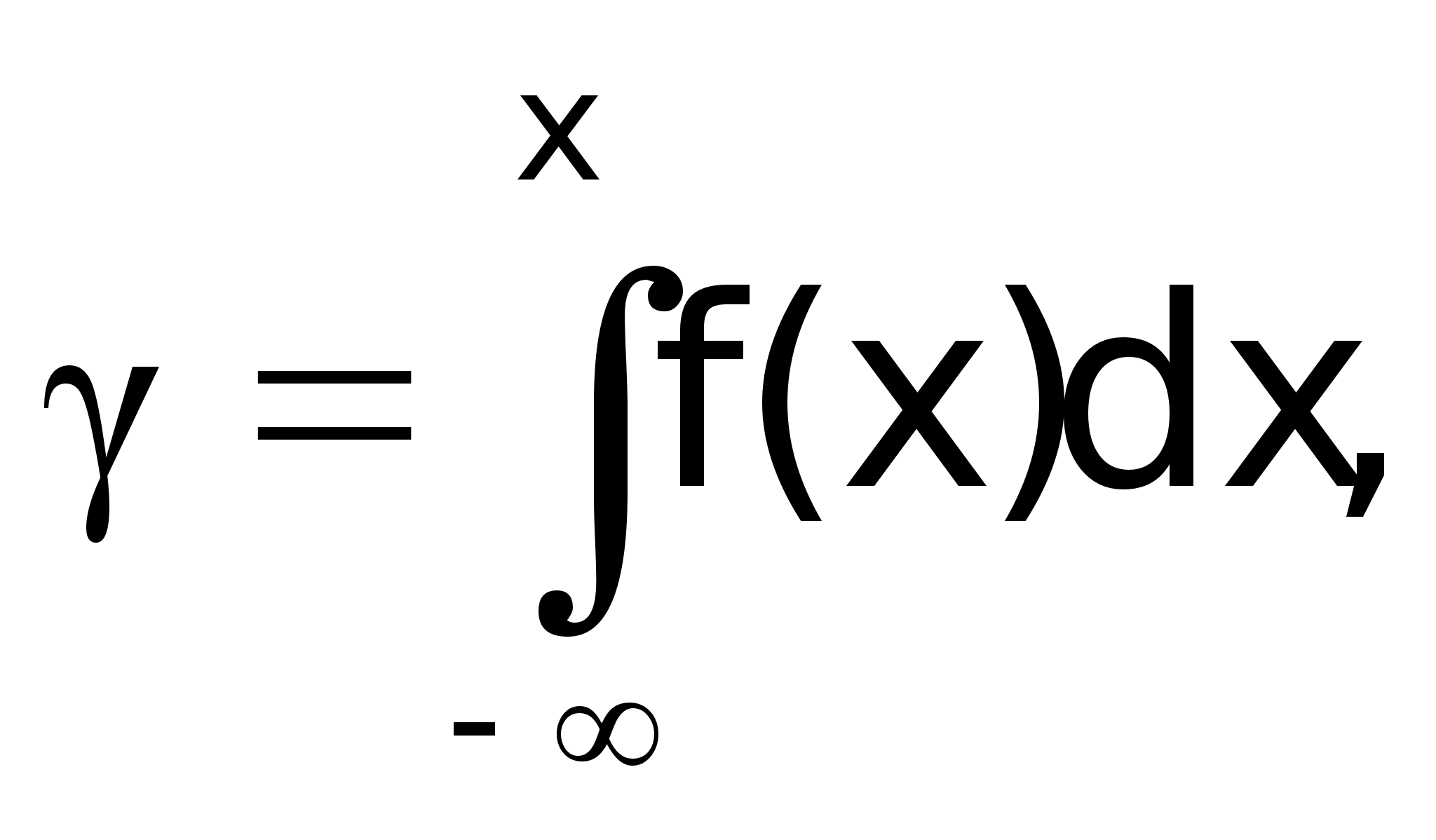
решить полученное
выражение
относительно
x.
Далее по построенному статистическому ряду значений R рассчитывается приближенное значение статистического среднего (математического ожидания) m*. Минимальное число испытаний определяется по формуле
Nmin=lg(1-)/lg(1-), (6)
где – заданная вероятность попадания при испытаниях в зону, ограниченную заданной точностью; – заданная точность.
Вычисление определенного интеграла производится численным методом по приближенной формуле Уэддля для шести значений подынтегральной функции:
г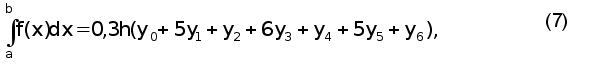
де
yi
– значения
подынтегральной
функции; h =(b-a)/6.
Значение b выбирается
настолько
большим, чтобы
интеграл
б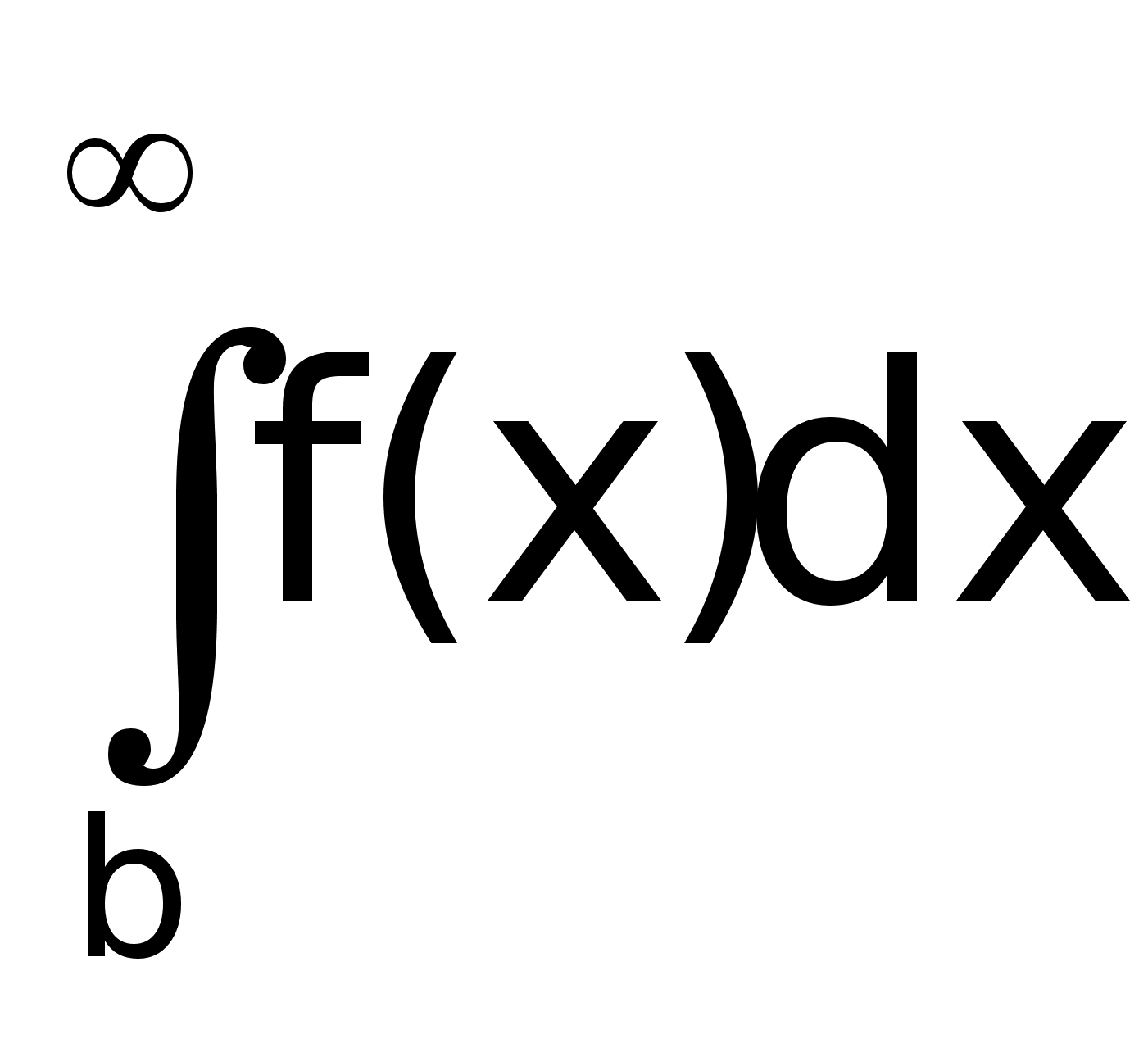
ыл
меньше какой-то
наперед заданной
величины погрешности.
Последовательность решения задачи 4
По таблице 11 выбирается значение k.
Таблица 11Значения k в зависимости от класса
подверженности внешним факторам риска
| Класс К подверженности внешним факторам риска | |||||
| 1 | 2 | 3 | 4 | 5 | |
| k | 1,312 | 1,458 | 1,620 | 1,800 | 2,000 |
Рассчитывается величина допустимого риска аварии R* (формула (3) ).
Записываются формулы преобразования от i к xi.
Определяется минимальное число испытаний Nmin (формула (6 ).
На отдельном листе оформляется таблица исходных данных для расчета на ЭВМ значения m*. Образец заполнения представлен в табл.12.
Таблица 12Образец заполнения таблицы исходных данных
| № | Наименование показателя | Значение показателя |
| 1 | Класс подверженности внешним факторам риска (K) | 1 |
Окончание табл. 12
| № | Наименование показателя | Значение показателя |
| 2 | Величина допустимого риска аварии (R*) | 22,169 |
| 3 | Формула преобразования п xп | xп=п(1-0,88)+0,88 |
| 4 | Формула преобразования м xм | xм=м(1-0,9)+0,9 |
| 5 | Формула преобразования с xс | xс=с(1-0,786)+0,786 |
| 6 | Число этажей (m) | 16 |
| 7 | Число нес. констр. на этаже (n) | 4 |
| 8 | Число нес. констр. на нулевом цикле (v) | 6 |
| 9 | Минимальное число испытаний (Nmin) | 5349 |
Производится расчет значения m* с использованием программного обеспечения кафедры «ЭиИ».
Результаты расчета на ЭВМ оформляются в соответствии с образцом, приведенным в приложении 4.
Рассчитывается PA (формулы (3), (7)). При определении верхней границы интегрирования в формуле (7) необходимо ориентироваться на результаты произведенных статистических испытаний.
Рассчитывается N – значение нетто-ставки страхового тарифа (формула (1)).
Литература к задаче 4
Вентцель Е.С. Основы исследования операций.– М.: Советское радио, 1972.
Габрин К.Э., Мельчаков Е.А., Мельчаков А.П. К методике назначения нетто-тарифа при страховании объектов строительства // Сб. ст. Южно-Уральского государственного университета «Проблемы совершенствования и развития экономических отношений в переходной экономике».–Челябинск: Изд-во ЮУрГУ, 2000.
Мельчаков А.П., Габрин К.Э. Технология обеспечения конструктивной безопасности строящихся зданий и сооружений // Известия ВУЗов. Строительство.–2000.–№ 2-3.–С. 114 – 117.
Шепелев И.Г. Математические методы и модели управления в строительстве.–М.:Высшая школа, 1980.
Приложение 1Таблица П1. F-распределение Фишера
| Значения F | |||||
| | 1=1 | 1=2 | 1=3 | 1=4 | |
| 2=10 | 0,05 | 4,96 | 4,10 | 3,71 | 3,48 |
| 0,10 | 10,04 | 7,56 | 6,55 | 5,99 | |
| 2=11 | 0,05 | 4,84 | 3,98 | 3,59 | 3,26 |
| 0,10 | 9,65 | 7,2 | 6,22 | 5,67 | |
| 2=12 | 0,05 | 4,75 | 3,88 | 3,36 | 3,41 |
| 0,10 | 9,33 | 7,2 | 5,67 | 5,74 | |
| 2=13 | 0,05 | 4,67 | 3,8 | 3,49 | 3,18 |
| 0,10 | 9,07 | 6,7 | 6,22 | 5,2 | |
| 2=14 | 0,05 | 4,60 | 3,74 | 3,34 | 3,11 |
| 0,10 | 8,86 | 6,51 | 5,56 | 5,03 | |
Таблица П2. t-распределение Стьюдента
| Значения t | ||
| | При =0,1 | При =0,05 |
| 10 | 1,812 | 2,228 |
| 11 | 1,796 | 2,201 |
| 12 | 1,782 | 2,179 |
| 13 | 1,771 | 2,160 |
| 14 | 1,761 | 2,145 |
Приложение 2
Текст программы численного решения
системы семи дифференциальных уравнений
Sub DU()
x1=1 'начальные условия при t=0
x2=0 'начальные условия при t=0
x3=0 'начальные условия при t=0
x4=0 'начальные условия при t=0
x5=0 ' начальные условия при t=0
x6=0 ' начальные условия при t=0
x7=0 ' начальные условия при t=0
Sheets("1").Cells(k+2;2).Value=x1
Sheets("1").Cells(k+2;3).Value=x2
Sheets("1").Cells(k+2;4).Value=x3
Sheets("1").Cells(k+2;5).Value=x4
Sheets("1").Cells(k+2;6).Value=x5
Sheets("1").Cells(k+2;7).Value=x6
Sheets("1").Cells(k+2;8).Value=x7
dt=30/50
a12=Sheets("1").Cells(5;9).Value ' инт. потока
a13=Sheets("1").Cells(5;10).Value ' инт. потока
a21=Sheets("1").Cells(5;11).Value ' инт. потока
a23=Sheets("1").Cells(5;12).Value ' инт. потока
a34=Sheets("1").Cells(5;13).Value ' инт. потока
a45=Sheets("1").Cells(5;14).Value ' инт. потока
a52=Sheets("1").Cells(5;15).Value ' инт. потока
a26=Sheets("1").Cells(5;16).Value ' инт. потока
a62=Sheets("1").Cells(5;17).Value ' инт. потока
a67=Sheets("1").Cells(5;18).Value ' инт. потока
a72=Sheets("1").Cells(5;19).Value ' инт. потока
For k = 0 To 50
k1=One(x1;x2;x3;x4;x5;x6;x7;a12;a13;a21)*dt
m1=Two(x1;x2;x3;x4;x5;x6;x7;a12;a26;a21;a23;a52;a62;a72)*dt
n1=Three(x1;x2;x3;x4;x5;x6;x7;a13;a23;a34)*dt
o1=Four(x1;x2;x3;x4;x5;x6;x7;a34;a45)*dt
p1=Five(x1;x2;x3;x4;x5;x6;x7;a45;a52)*dt
r1=Six(x1;x2;x3;x4;x5;x6;x7;a26;a67;a62)*dt
s1=Seven(x1;x2;x3;x4;x5;x6;x7;a67;a72)*dt
k2=One(x1+0,5*k1;x2+0,5*m1;x3+0,5*n1;x4+0,5*o1;x5+0,5*p1; x6+0,5*r1;x7+0,5*s1;a12;a13;a21)*dt
m2=Two(x1+0,5*k1;x2+0,5*m1;x3+0,5*n1;x4+0,5*o1;x5+0,5*p1; x6+0,5*r1;x7+0,5*s1;a12;a26;a21;a23;a52;a62;a72)*dt
n2=Three(x1+0,5*k1;x2+0,5*m1;x3+0,5*n1;x4+0,5*o1;x5+0,5*p1;x6+0,5*r1;x7+0,5*s1;a13;a23;a34)*dt
o1=Four(x1+0,5*k1;x2+0,5*m1;x3+0,5*n1;x4+0,5*o1;x5+0,5*p1;x6+0,5*r1;x7+0,5*s1;a34;a45)*dt
p1=Five(x1+0,5*k1;x2+0,5*m1;x3+0,5*n1;x4+0,5*o1;x5+0,5*p1;x6+0,5*r1;x7+0,5*s1;a45;a52)*dt
r1=Six(x1+0,5*k1;x2+0,5*m1;x3+0,5*n1;x4+0,5*o1;x5+0,5*p1;x6+0,5*r1;x7+0,5*s1;a26;a67;a62)*dt
s1=Seven(x1+0,5*k1;x2+0,5*m1;x3+0,5*n1;x4+0,5*o1;x5+0,5*p1;x6+0,5*r1;x7+0,5*s1;a67;a72)*dt
k3=One(x1+0,5*k2;x2+0,5*m2;x3+0,5*n2;x4+0,5*o2;x5+0,5*p2;x6+0,5*r2;x7+0,5*s2;a12;a13;a21)*dt
m3=Two(x1+0,5*k2;x2+0,5*m2;x3+0,5*n2;x4+0,5*o2;x5+0,5*p2;x6+0,5*r2;x7+0,5*s2;a12;a26;a21;a23;a52;a62;a72)*dt
n3=Three(x1+0,5*k2;x2+0,5*m2;x3+0,5*n2;x4+0,5*o2;x5+0,5*p2;x6+0,5*r2;x7+0,5*s2;a13;a23;a34)*dt
o3=Four(x1+0,5*k2;x2+0,5*m2;x3+0,5*n2;x4+0,5*o2;x5+0,5*p2;x6+0,5*r2;x7+0,5*s2;a34;a45)*dt
p3=Five(x1+0,5*k2;x2+0,5*m2;x3+0,5*n2;x4+0,5*o2;x5+0,5*p2;x6+0,5*r2;x7+0,5*s2;a45;a52)*dt
r3=Six(x1+0,5*k2;x2+0,5*m2;x3+0,5*n2;x4+0,5*o2;x5+0,5*p2; x6+0,5*r2;x7+0,5*s2;a26;a67;a62)*dt
s3=Seven(x1+0,5*k2;x2+0,5*m2;x3+0,5*n2;x4+0,5*o2;x5+0,5*p2;x6+0,5*r2;x7+0,5*s2;a67;a72)*dt
k4=One(x1+k3;x2+m3;x3+n3;x4+o3;x5+p3;x6+r3;x7+s3;a12;a13;a21)*dt
m4=Two(x1+k3;x2+m3;x3+n3;x4+o3;x5+p3;x6+r3;x7+s3;a12;a26;a21;a23;a52;a62;a72)*dt
n4=Three(x1+k3;x2+m3;x3+n3;x4+o3;x5+p3;x6+r3;x7+s3;a13;a23;a34)*dt
o4=Four(x1+k3;x2+m3;x3+n3;x4+o3;x5+p3;x6+r3;x7+s3;a34;a45)*dt
p4=Five(x1+k3;x2+m3;x3+n3;x4+o3;x5+p3;x6+r3;x7+s3;a45;a52)*dt
r4=Six(x1+k3;x2+m3;x3+n3;x4+o3;x5+p3;x6+r3;x7+s3;a26;a67;a62)*dt
s4=Seven(x1+k3;x2+m3;x3+n3;x4+o3;x5+p3;x6+r3;x7+s3;a67;a72)*dt
x1=x1+(k1+2*k2+2*k3+k4)/6
x2=x2+(m1+2*m2+2*m3+m4)/6
x3=x3+(n1+2*n2+2*n3+n4)/6
x4=x4+(o1+2*o2+2*o3+o4)/6
x5=x5+(p1+2*p2+2*p3+p4)/6
x6=x6+(r1+2*r2+2*r3+r4)/6
x7=x7+(s1+2*s2+2*s3+s4)/6
Sheets("1").Cells(k+3;2).Value=x1
Sheets("1").Cells(k+3;3).Value=x2
Sheets("1").Cells(k+3;4).Value=x3
Sheets("1").Cells(k+3;5).Value=x4
Sheets("1").Cells(k+3;6).Value=x5
Sheets("1").Cells(k+3;7).Value=x6
Sheets("1").Cells(k+3;8).Value=x7
Next
End Sub
Function One(x1;x2;x3;x4;x5;x6;x7;a12;a13;a21)'Вер.P1
One=-(a12+a13)*x1+a21*x2
End Function
FunctionTwo(x1;x2;x3;x4;x5;x6;x7;a12;a26;a21;a23;a52;a62;a72)'Вер.P4
Two=a12*x1-(a26+a21+a23)*x2+a52*x5+a62*x6+a72*x7
End Function
Function Three(x1;x2;x3;x4;x5;x6;x7;a13;a23;a34)'Вер.P3
Three=a13*x1+a23*x2-a34*x3
End Function
Function Four(x1;x2;x3;x4;x5;x6;x7;a34;a45)'Вер.Р4
Four=a34*x3-a45*x4
End Function
Function Five(x1;x2;x3;x4;x5;x6;x7;a45;a52)'Вер.Р5
Five=a45*x4-a52*x5
End Function
Function Six(x1;x2;x3;x4;x5;x6;x7;a26;a67;a62)'Вер.Р6
Six=a26*x2-(a67+a62)*x6
End Function
Function Seven(x1;x2;x3;x4;x5;x6;x7;a67;a72)'Вер.Р7
Seven=a67*x6-a72*x7
End Function
Приложение 3 Оформление рабочего листа MS EXCEL в задаче 3
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | |
| 1 | P1 | P2 | P3 | P4 | P5 | P6 | R | ||||||||||||
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | ||
| 3 | 2 | 9,33E-1 | 6,61E-02 | 7,86E-04 | 4,49E-04 | 2,49E-05 | 3,58E-05 | 1,87E-06 | 433 | 4 | 0,4 | 0,5 | 3 | 2 | 624 | 2,6 | 3,5 | ||
| 4 | 3 | 9,13E-1 | 8,39E-02 | 1,04E-03 | 1,12E-03 | 1,23E-04 | 7,14E-05 | 9,83E-06 | 12 | 13 | 21 | 23 | 34 | 45 | 52 | 26 | 62 | 67 | 72 |
| 5 | 4 | 9,07E-1 | 8,87E-02 | 1,11E-03 | 1,79E-03 | 2,85E-04 | 1,00E-04 | 2,17E-05 | 0,25 | 0,002 | 2,5 | 0,002 | 2 | 0,33 | 0,5 | 0,002 | 0,39 | 0,39 | 0,29 |
|
| 5 | 9,04E-1 | 8,99E-02 | 1,14E-03 | 2,41E-03 | 4,94E-04 | 1,22E-04 | 3,60E-05 | |||||||||||
| 7 | 6 | 9,03E-1 | 9,02E-02 | 1,14E-03 | 2,96E-03 | 7,34E-04 | 1,39E-04 | 5,14E-05 | |||||||||||
| 8 | 7 | 9,02E-1 | 9,03E-02 | 1,15E-03 | 3,44E-03 | 9,92E-04 | 1,52E-04 | 6,71E-05 | |||||||||||
| 9 | 8 | 9,01E-1 | 9,02E-02 | 1,14E-03 | 3,86E-03 | 1,26E-03 | 1,61E-04 | 8,26E-05 | |||||||||||
| 10 | 9 | 9,00E-1 | 9,02E-02 | 1,14E-03 | 4,23E-03 | 1,52E-03 | 1,68E-04 | 9,76E-05 | |||||||||||
| 11 | 10 | 8,99E-1 | 9,02E-02 | 1,14E-03 | 4,56E-03 | 1,78E-03 | 1,73E-04 | 1,12E-04 | |||||||||||
| 12 | 11 | 8,98E-1 | 9,01E-02 | 1,14E-03 | 4,84E-03 | 2,02E-03 | 1,77E-04 | 1,25E-04 | |||||||||||
| … | … | … | … | … | … | … | … | … | |||||||||||
| 34 | 33 | 8,92E-1 | 9,00E-02 | 1,13E-03 | 6,70E-03 | 4,34E-03 | 1,87E-04 | 2,41E-04 | |||||||||||
| 35 | 34 | 8,92E-1 | 9,00E-02 | 1,13E-03 | 6,71E-03 | 4,37E-03 | 1,87E-04 | 2,42E-04 | |||||||||||
| 36 | 35 | 8,92E-1 | 9,00E-02 | 1,13E-03 | 6,72E-03 | 4,39E-03 | 1,87E-04 | 2,43E-04 | |||||||||||
| 37 | 36 | 8,92E-1 | 9,00E-02 | 1,13E-03 | 6,73E-03 | 4,40E-03 | 1,87E-04 | 2,44E-04 | |||||||||||
| 38 | 37 | 8,92E-1 | 9,00E-02 | 1,13E-03 | 6,74E-03 | 4,42E-03 | 1,87E-04 | 2,45E-04 | |||||||||||
| 39 | 38 | 8,92E-1 | 9,00E-02 | 1,13E-03 | 6,75E-03 | 4,43E-03 | 1,87E-04 | 2,46E-04 | |||||||||||
|
| 39 | 8,92E-1 | 9,00E-02 | 1,13E-03 | 6,76E-03 | 4,45E-03 | 1,87E-04 | 2,47E-04 | |||||||||||
| 41 | 40 | 8,91E-1 | 9,00E-02 | 1,13E-03 | 6,76E-03 | 4,46E-03 | 1,87E-04 | 2,47E-04 | |||||||||||
| 42 | 41 | 8,91E-1 | 9,00E-02 | 1,13E-03 | 6,77E-03 | 4,47E-03 | 1,87E-04 | 2,48E-04 | |||||||||||
| 43 | 42 | 8,91E-1 | 9,00E-02 | 1,13E-03 | 6,77E-03 | 4,47E-03 | 1,87E-04 | 2,48E-04 | |||||||||||
| 44 | 43 | 8,91E-1 | 9,00E-02 | 1,13E-03 | 6,77E-03 | 4,48E-03 | 1,87E-04 | 2,49E-04 | |||||||||||
| 45 | 44 | 8,91E-1 | 9,00E-02 | 1,13E-03 | 6,78E-03 | 4,49E-03 | 1,87E-04 | 2,49E-04 | |||||||||||
| 46 | 45 | 8,91E-1 | 9,00E-02 | 1,13E-03 | 6,78E-03 | 4,49E-03 | 1,87E-04 | 2,49E-04 | |||||||||||
| 47 | 46 | 8,91E-01 | 9,00E-02 | 1,13E-03 | 6,78E-03 | 4,50E-03 | 1,87E-04 | 2,50E-04 | |||||||||||
| 48 | 47 | 8,91E-01 | 9,00E-02 | 1,13E-03 | 6,78E-03 | 4,50E-03 | 1,87E-04 | 2,50E-04 | |||||||||||
| 49 | 48 | 8,91E-01 | 9,00E-02 | 1,13E-03 | 6,79E-03 | 4,51E-03 | 1,87E-04 | 2,50E-04 | |||||||||||
| 50 | 49 | 8,91E-01 | 9,00E-02 | 1,13E-03 | 6,79E-03 | 4,51E-03 | 1,87E-04 | 2,50E-04 | |||||||||||
| 51 | 50 | 8,91E-01 | 9,00E-02 | 1,13E-03 | 6,79E-03 | 4,51E-03 | 1,87E-04 | 2,51E-04 | |||||||||||
| 52 | 51 | 8,91E-01 | 9,00E-02 | 1,13E-03 | 6,79E-03 | 4,51E-03 | 1,87E-04 | 2,51E-04 | |||||||||||
| 53 | 52 | 8,91E-01 | 9,00E-02 | 1,13E-03 | 6,79E-03 | 4,52E-03 | 1,87E-04 | 2,51E-04 |
О
P6
P7
ГЛАВЛЕНИЕ Задача 1. Многофакторный регрессионный и корреляционный анализ 3 Методические указания к решению задачи 1 6 Пример решения задачи 1 10 Литература к задаче 1 16 Задача 2. Динамическое программирование 17 Методические указания к решению задачи 2 18 Литература к задаче 2 20 Задача 3. Марковские случайные процессы 20 Методические указания к решению задачи 3 24 Литература к задаче 3 24 Задача 4. Метод Монте-Карло 25 Методические указания к решению задачи 4 28 Последовательность решения задачи 4 30 Литература к задаче 4 31 Приложение 1 32 Приложение 2 32 Приложение 3 35 Приложение 4 37Габрин Константин Эдуардович МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ Семестровое задание и методические указания к решению задач
Похожие работы
... -педагогическая или научно-техническая проблема, являющаяся новым научным вкладом в теорию определенной области знаний (педагогику, технику и другие). 4. ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ВЫПОЛНЕНИЯ ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЫ БАКАЛАВРА ФИЗИКО-МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ПРОФИЛЬ ИНФОРМАТИКА 4.1. Положение о выпускной квалификационной работе бакалавра физико-математического образования: ...
... посредством организации конкурсов бизнес-идей, мини-олимпиад, работы творческих групп и пр. С целью их проведения в исследовании разработан сборник экономических задач, основанный на предложенном подходе к интеграции математического и экономического содержания, рассмотрена технология организации такого типа мероприятий. Трудности применения математических методов в экономике Трудности ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
 6
6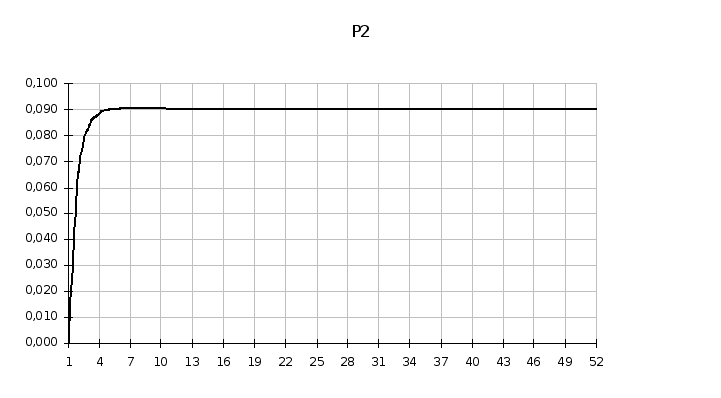 40
40

0 комментариев