Группы геометрических преобразований. Группы вращений, подобий, гомотетий с заданным общим центром, параллельных переносов
Арифметические функции: t(n), s(n), j(n)
Алгоритм Евклида и его применения
Линейное представление наибольшего общего делителя
Базис пространства решений однородной системы линейных уравнений - это фундаментальная система решений
Корни многочлена; схема Горнера; теорема Безу
Разложение многочлена в произведение неприводимых
Теорема о строении простого алгебраического расширения
Навигация
Группы геометрических преобразований. Группы вращений, подобий, гомотетий с заданным общим центром, параллельных переносов
Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета
38950
знаков
13
таблиц
4
изображения
4. Группы геометрических преобразований. Группы вращений, подобий, гомотетий с заданным общим центром, параллельных переносов.
5. Матричные группы. Укажем на две важнейшие матричные группы:
GLn(R) - полная линейная группа (группа обратимых матриц),
SLn(R) - специальная линейная группа
(группа матриц с единичным определителем),
30. Арифметика группы: обратные элементы, степени с целым показателем.
При описании таблицы Кэли группы симметрий правильного треугольника мы использовали так называемые арифметические свойства элементов группы. Отметим важнейшие из них в следующей теореме.
Теорема. Пусть (G,×) - группа. Тогда для ее элементов справедливы равенства:
(а) (xy)(zt) = x(y(zt) = ((xy)z)t;
(б) (xy)-1 = y-1x-1;
(в) (xp)q = xpq; xpxq = xp+q для любых целых p, q.
Доказательство. Проверим только пункт (б). Имеем:
(xy)(y-1x-1) = x(yy-1)x-1 = x(1)x-1 = 1,
(y-1x-1)(xy) = y-1(x-1x)y = y-1(1)y = 1;
откуда и получаем требуемое утверждение. ÿ
40. Решение в группах линейных уравнений. В качестве применения простейших свойств приведем следующий простой результат.
Теорема. В произвольной мультипликативной группе G однозначно разрешимо каждое из уравнений:
ax = b, ya = b, где a, b - фиксированные элементы группы.
Доказательство. Допустим, что элемент g удовлетворяет равенству ag = b. Тогда умножая обе части равенства слева на элемент обратный к g, получим
a-1(ag) = a-1b, откуда находим g = a-1b. Легко проверить, что элемент a-1b является решением уравнения ax = b, т.е. справедливо равенство a(a-1b) = b.
Аналогично доказывается разрешимость второго уравнения. ÿ
Примеры. 1. Решить уравнение (12)x = (13) в группе подстановок S3.
Имеем: x = (12)(13) = (123).
2. Решить уравнение rx = a в группе симметрий правильного треугольника.
Имеем: x = r -1a = g, поскольку sa является отражением и
C(sa) = (Cs)a = Ba = C.
3. Решить уравнение X 
= 
в группе GL2(R).
Имеем:
X = 
=
=
.
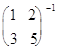2. Кольца и поля; примеры и простейшие свойства элементов
10. Определение кольца и поля.
Определение. Непустое множество A, на котором заданы операции сложения и умножения, называется кольцом, если выполнены следующие два условия:
а) (A, +) - абелева группа;
б) умножение дистрибутивно относительно сложения, т.е. для любых элементов x, y, z из A выполнены равенства: (x + y)z = xz + yz; x(y + z) = xy + xz.
Определение. Кольцо называется коммутативным, если операция умножения в нем коммутативна; кольцо называется ассоциативным, если операция умножения в нем ассоциативна. Кольцо называется кольцом с единицей, если оно обладает нейтральным элементом относительно умножения.
Определение. Пусть A - ассоциативное кольцо с единицей 1. Элемент aÎA называется обратимым, если существует элемент bÎA такой, что ab = ba = 1.
Легко проверить, что элемент b, о котором идет речь находится однозначно, поэтому он обозначается a-1 и называется элементом обратным к a.
Важнейшим типом колец являются поля.
Определение. Ассоциативно-коммутативное кольцо с единицей называется полем, если в нем всякий ненулевой элемент обратим.
20. Примеры колец: числовые кольца, кольца многочленов, кольца последовательностей и функций, кольца матриц, кольца вычетов.
Если группы появляются, прежде всего, как группы обратимых отображений, то возникновение понятия кольца связано с изучением важнейших числовых систем и многочленов.
1. Числовые кольца (кольца, элементы которых являются комплексными числами):
а) (классические числовые кольца) кольцо целых чисел Z, кольцо рациональных чисел Q, кольцо действительных чисел R, кольцо комплексных чисел C.
б) кольцо Z[i] целых гауссовых чисел вида a + bi, где a, b - целые числа;
г) кольцо Z[
] действительных чисел вида a + b с целыми a, b.
2. Кольца многочленов R[x], Q[x], Z[x], C[x] от одной переменной x с действительными, рациональными, целыми и комплексными коэффициентами.
3. Кольца последовательностей и функций. Среди этих колец выделим особо:
а) кольцо последовательностей действительных чисел с обычными операциями сложения и умножения последовательностей;
б) кольцо ограниченных последовательностей действительных чисел;
в) кольцо фундаментальных последовательностей;
г) кольцо непрерывных действительно-значных функций на отрезке [0 , 1].
4. Кольца матриц. Среди разнообразных матричных колец выделим следующие:
а) полное матричное кольцо Mn(A) над кольцом A или кольцо квадратных матриц порядка n с элементами из кольца A, в качестве кольца коэффициентов A можно рассматривать, в частности, любое числовое кольцо;
б) кольцо Dn(A) диагональных матриц, т.е. матриц, у которых вне главной диагонали находятся только нулевые элементы;
в) кольцо TNn(A) нильтреугольных матриц, т.е. треугольных матриц с нулями на главной диагонали.
Кольца Mn и TNn являются некоммутативными, в кольце TNn нет единицы.
30. Примеры полей.
1. Числовые поля. Q, R, C, Q[i], Q[] .
2. Поля дробно-рациональных функций: Q(x), R(x), C(x). Так, элементами множества R(x) являются всевозможные функции вида 
, где f(x), g(x) - многочлены с действительными коэффициентами, причем многочлен g(x) ненулевой. Операции сложения и умножения дробей обычные.
3. Поле вычетов Zp по простому модулю p. Например, для p=7 утверждение получается из следующих равенств в кольце Z7: 2Ä4 = 3Ä5 = 6Ä6 = 1.
40. Арифметика колец и полей. Важнейшие арифметические свойства элементов колец и полей приведены в теоремах.
Теорема. Для любых элементов кольца справедливы равенства:
(а) 0×x = x×0 = 0;
(б) правило знаков: x(- y) = (-x)y = -(xy);
(в) (дистрибутивность умножения относительно разности)
(x - y)z = xz - yz, x(y - z) = xy - xz;
где разность определяется обычным образом x - y := x + (- y).
Доказательство. (а) Имеем: 0×x = (0 + 0)×x = 0×x +0×x, откуда 0×x = 0. Аналогично проверяется и второе равенство x×0 = 0.
(б) Имеем: 0 = x×0 = x×(y + (-y)) = x×y +x×(-y), откуда x×(-y) = -(x×y).
(в) Имеем: (x - y)z =(x + (- y))z = x×z + (-y)×z = x×z - y×z. ÿ
Обозначение. 
:= a×b-1, если a, b - элементы поля, причем b ¹ 0.
Теорема. В поле справедливы обычные правила работы с дробями:
(а) основное свойство дроби: ("c¹0) 
;
(б) правила сложения дробей: 
,
;
(в) правило умножения дробей: 
;
(г)
, если ab ¹ 0;
в частности, справедливо известное правило деления дробей.
Доказательство. (а) Действительно, 
= (ac)×(bc)-1 = acc-1b = a×b-1 = .
(б) Имеем: 
= (a + c)×b-1 = a×b-1 + c×b-1 = 
. И далее на основании уже доказанных свойств получаем 
.
Аналогично проверяются и два оставшихся пункта. ÿ
Похожие работы
... учебного процесса методической подготовки будущего учителя. Основное содержание исследования отражено в следующих публикациях автора: I. Монографии: 1. Абдуразаков М.М. Совершенствования содержания подготовки будущего учителя информатики в условиях информатизации образования. –Махачкала: ДГПУ, 2006. –190 с. 12 п.л. 2. Гаджиев Г.М., Абдуразаков М.М. Технология преподавания информатики. – ...
... профиля и специализации. На факультетах общественных наук предметы, входившие в минимум, изучались в расширенном объеме[4]. 2. Положение русского студенчества в конце XIX начале XX века 2.1 Образ русского студента в конце XIX начале XX века В отличие от закрытых учебных заведений, в которых учились в основном дворяне, значительное число учащихся в университетах были людьми незнатными ...
... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...
... покровителей, сделавших особый вклад в развитие культуры, в Европе называют медичи. Конец девятнадцатого века в России был ознаменован необычайным подъёмом культуры. В связи с этим появились в стране и те, кто этот подъём всячески поддерживал, в том числе и материально. Эти люди были в основном богатыми купцами и промышленниками, которые чувствовали необычайный прогресс в развитии культуры ...
0 комментариев