Группы геометрических преобразований. Группы вращений, подобий, гомотетий с заданным общим центром, параллельных переносов
Арифметические функции: t(n), s(n), j(n)
Алгоритм Евклида и его применения
Линейное представление наибольшего общего делителя
Базис пространства решений однородной системы линейных уравнений - это фундаментальная система решений
Корни многочлена; схема Горнера; теорема Безу
Разложение многочлена в произведение неприводимых
Теорема о строении простого алгебраического расширения
Навигация
Арифметические функции: t(n), s(n), j(n)
Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета
38950
знаков
13
таблиц
4
изображения
3. Арифметические функции: t(n), s(n), j(n).
10. Полная мультипликативность.
Определение. Числовой (арифметической) функцией называется функция, определенная на множестве Z+ целых положительных чисел и принимающая комплексные значения.
Числовая функция q называется вполне мультипликативной, если выполнены условия:
(1) ($x) q(x)¹0,
(2) для любых взаимно простых чисел x и y
q(xy)= q(x) q(y).
Заметим, что непосредственно из определения вытекает равенство
q(1)=1.
В самом деле, q(1)¹0, так как иначе данная функция q была бы нулевой; q(1)= q(1×1)= q(1) q(1), следовательно, q(1)=1.
Легко проверить, что каждая из следующих функций
q(x)=1, q(x)= x, q(x)= x-1,
вполне мультипликативна.
Следующая теорема позволяет существенно расширить запас вполне мультипликативных функций.
Теорема. Произведение вполне мультипликативных функций является вполне мультипликативной функцией.
Доказательство. Пусть числа x и y взаимно просты, а функции f и g вполне мультипликативны. Тогда, обозначив через h произведение функций f и g, имеем:
h(xy)=f(xy)g(xy)=f(x)f(y)g(x)g(y)=[f(x)g(x)][f(y)g(y)]=
=h(x)h(y).
Следствие. Для любого целого k функция q(x)= xk вполне мультипликативна.
20. Сумма значений функции по всем делителям аргумента.
Введем в рассмотрение, наряду с функцией q(x), функцию
,
равную сумме всех значений функции q(d) при условии, что переменная d пробегает все делители числа x.
Теорема (основное тождество). Если x=
, то
×
.
В частности, если функция q вполне мультипликативна, то и функция 
также вполне мультипликативна.
Доказательство. Рассмотрим произведение сумм, находящееся в правой части требуемого равенства:
=
=
=
.
Осталось заметить, что для каждого набора (g1, g2,..., gk) целых неотрицательных чисел gi, не превосходящих ai, в сумме
каждое слагаемое встречается ровно один раз. Учитывая теперь, что каждый делитель числа имеет вид 
, получаем
=
.
Свойство полной мультипликативности рассматриваемой функции немедленно вытекает из того, что взаимно простые числа содержат различные простые сомножители. ÿ
30. Число делителей t(x) и сумма делителей s(x).
Рассмотрим следующие вполне мультипликативные функции:
t(x)= 
, где q(x)=1, - число делителей числа x,
s(x)= , где q(x) = x, - сумма делителей числа x.
Теорема. Справедливы тождества:
t(
)=(a1 + 1)( a2 + 1)...( ak + 1),
s(
)=
.
Доказательство. а) Из определения функции t(x) немедленно следует указанное тождество, поскольку в силу основного тождества легко подсчитать число слагаемых, каждое из которых равно 1, в каждой из скобок соответствующего произведения.
б) Это тождество получается из основного тождества и формулы суммы членов геометрической прогрессии:
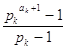.ÿ
40. Функция Эйлера. Одной из важнейших числовых функций является следующая функция, впервые введенная в рассмотрение Эйлером.
Определение. Через j(x) обозначается количество чисел ряда
1, 2, ..., x, (*)
взаимно простых с числом x.
Справедлива следующая теорема, которую приведем без доказательства.
Теорема. Если x=, то
j(x)= x×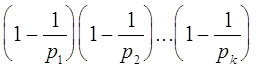 
.
Следствие. Функция Эйлера вполне мультипликативна и
.
Теорема (тождество Гаусса). 
.
Доказательство. Применяя основное тождество и последнее следствие, получаем, считая 
,
. ÿ
Похожие работы
... учебного процесса методической подготовки будущего учителя. Основное содержание исследования отражено в следующих публикациях автора: I. Монографии: 1. Абдуразаков М.М. Совершенствования содержания подготовки будущего учителя информатики в условиях информатизации образования. –Махачкала: ДГПУ, 2006. –190 с. 12 п.л. 2. Гаджиев Г.М., Абдуразаков М.М. Технология преподавания информатики. – ...
... профиля и специализации. На факультетах общественных наук предметы, входившие в минимум, изучались в расширенном объеме[4]. 2. Положение русского студенчества в конце XIX начале XX века 2.1 Образ русского студента в конце XIX начале XX века В отличие от закрытых учебных заведений, в которых учились в основном дворяне, значительное число учащихся в университетах были людьми незнатными ...
... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...
... покровителей, сделавших особый вклад в развитие культуры, в Европе называют медичи. Конец девятнадцатого века в России был ознаменован необычайным подъёмом культуры. В связи с этим появились в стране и те, кто этот подъём всячески поддерживал, в том числе и материально. Эти люди были в основном богатыми купцами и промышленниками, которые чувствовали необычайный прогресс в развитии культуры ...
0 комментариев