Навигация
Строим в ПСК хОа графики функций
3. Строим в ПСК хОа графики функций
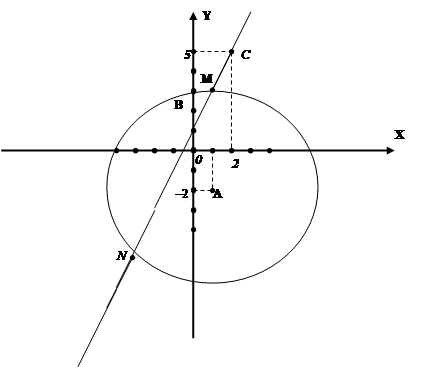
![]()
и нумеруем образовавшиеся области (оси роли не играют). Получилось девять областей.
4. Ищем, какая из областей подходит для данного неравенства, для чего берем точку из области и подставляем в неравенство.
Для наглядности составим таблицу.
| № | точка | неравенство: | вывод |
| 1 |
|
| - |
| 2 |
|
| + |
| 3 |
|
| - |
| 4 |
|
| + |
| 5 |
|
| - |
| 6 |
|
| + |
| 7 |
|
| - |
| 8 |
|
| + |
| 9 |
|
| - |
5. Найдем точки пересечения графиков
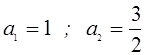
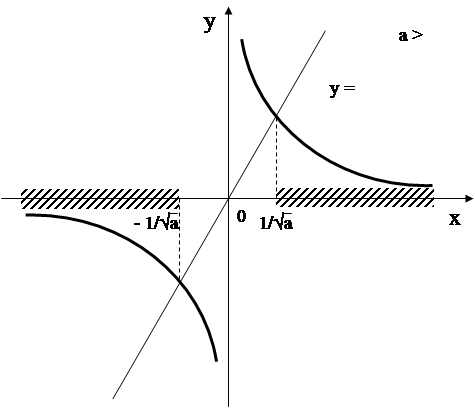
6. Зададим прямую а=сonst и будем сдвигать её от -¥ до +¥.
Ответ.
при ![]()
![]()
при ![]()
![]()
при ![]()
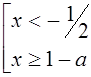
при ![]() решений нет
решений нет
при ![]()
![]()
Литература
1. Далингер В. А. “Геометрия помогает алгебре”. Издательство “Школа - Пресс”. Москва 1996 г.
2. Далингер В. А. “Все для обеспечения успеха на выпускных и вступительных экзаменах по математике”. Издательство Омского педуниверситета. Омск 1995 г.
3. Окунев А. А. “Графическое решение уравнений с параметрами”. Издательство “Школа - Пресс”. Москва 1986 г.
4. Письменский Д. Т. “Математика для старшеклассников”. Издательство “Айрис”. Москва 1996 г.
5. Ястрибинецкий Г. А. “Уравнений и неравенства, содержащие параметры”. Издательство “Просвещение”. Москва 1972 г.
6. Г. Корн и Т.Корн “Справочник по математике”. Издательство “Наука” физико–математическая литература. Москва 1977 г.
7. Амелькин В. В. и Рабцевич В. Л. “Задачи с параметрами” . Издательство “Асар”. Минск 1996 г.
Похожие работы
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... ;[0; 1), тогда x – x +1 = 1; 1 = 1 Þ x — любое число из [0; 1). В) x Î[1; ¥), тогда x + x – 1 = 1; 2x = 2; x = 1 Î[1; ¥). Ответ: x Î[0; 1]. Основные методы решения рациональных уравнений. 1) Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по ...
... функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения. Ответ. . Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих ...
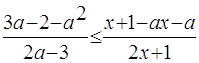


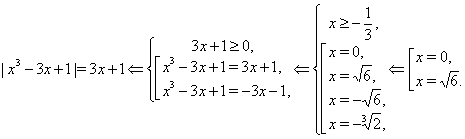
0 комментариев