Навигация
По графику определяем, при каких значениях а уравнение (5) имеет решение и при каких – не имеет решения
4. По графику определяем, при каких значениях а уравнение (5) имеет решение и при каких – не имеет решения.
Ответ:
если ![]() , то
, то 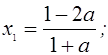
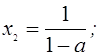
если ![]() , то
, то 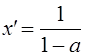 ;
;
если ![]() , то решений нет;
, то решений нет;
если ![]() , то
, то 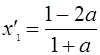 ,
, 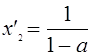 .
.
VI. Каким условиям должны удовлетворять те значения параметров ![]() и
и ![]() , при которых системы
, при которых системы
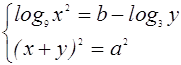 (1)
(1)
и
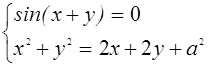 (2)
(2)
имеют одинаковое число решений ?
Решение.
С учетом того, что ![]() имеет смысл только при
имеет смысл только при ![]() , получаем после преобразований систему
, получаем после преобразований систему
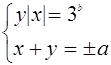 (3)
(3)
равносильную системе (1).
Система (2) равносильна системе
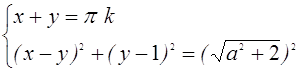 (4)
(4)
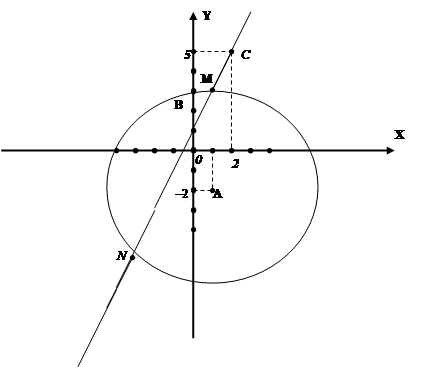
Первое уравнение системы (4) задает в плоскости хОу семейство прямых, второе уравнение задает семейство концентрических окружностей с центром в точке А(1;1) и радиусом ![]()
Поскольку ![]() , а
, а ![]() , то
, то ![]() , и, следовательно, система (4) имеет не менее четырех решений. При
, и, следовательно, система (4) имеет не менее четырех решений. При ![]() окружность касается прямой
окружность касается прямой ![]() и система (4) имеет пять решений.
и система (4) имеет пять решений.
Таким образом, если ![]() , то система (4) имеет четыре решения, если
, то система (4) имеет четыре решения, если ![]() , то таких решений будет больше, чем четыре.
, то таких решений будет больше, чем четыре.
Если же иметь в виду не радиусы окружностей, а сам параметр а, то система (4) имеет четыре решения в случае, когда ![]() , и больше четырех решений, если
, и больше четырех решений, если ![]() .
.
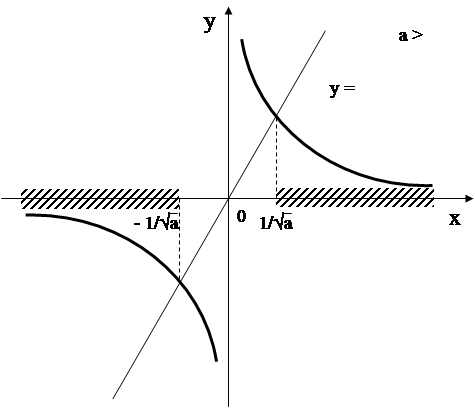
Обратимся теперь к рассмотрению системы (3). Первое уравнение этой системы задаёт в плоскости хОу семейство гипербол, расположенных в первом и втором квадрантах. Второе уравнение системы (3) задает в плоскости хОу семейство прямых.
При фиксированных положительных а и b система (3) может иметь два, три, или четыре решения. Число же решений зависит от того, будет ли прямая, заданная уравнением ![]() , иметь общие точки с гиперболой
, иметь общие точки с гиперболой ![]() при
при ![]() (прямая
(прямая ![]() всегда имеет одну точку пересечения с графиком функции
всегда имеет одну точку пересечения с графиком функции ![]() ).
).
Для решения этого рассмотрим уравнение
![]() ,
,
которое удобнее переписать в виде
![]()
Теперь решение задачи сводится к рассмотрению дискриминанта D последнего уравнения:
* если ![]() , т.е. если
, т.е. если ![]() , то система (3) имеет два решения;
, то система (3) имеет два решения;
* если ![]() , то система (3) имеет три решения;
, то система (3) имеет три решения;
* если ![]() , то система (3) имеет четыре решения.
, то система (3) имеет четыре решения.
Таким образом, одинаковое число решений у систем (1) и (2) – это четыре. И это имеет место, когда ![]() .
.
Ответ: ![]()
II. Неравенства с параметрами.
§1. Основные определения
Неравенство
¦(a, b, c, …, k, x)>j(a, b, c, …, k, x), (1)
где a, b, c, …, k – параметры, а x – действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.
Любая система значений параметров а = а0, b = b0, c = c0, …, k = k0, при некоторой функции
¦(a, b, c, …, k, x) и
j(a, b, c, …, k, x
имеют смысл в области действительных чисел, называется системой допустимых значений параметров.
![]() называется допустимым значением х, если
называется допустимым значением х, если
¦(a, b, c, …, k, x) и
j(a, b, c, …, k, x
принимают действительные значения при любой допустимой системе значений параметров.
Множество всех допустимых значений х называется областью определения неравенства (1).
Действительное число х0 называется частным решением неравенства (1), если неравенство
¦(a, b, c, …, k, x0)>j(a, b, c, …, k, x0)
верно при любой системе допустимых значений параметров.
Совокупность всех частных решений неравенства (1) называется общим решением этого неравенства.
Решить неравенство (1) – значит указать, при каких значениях параметров существует общее решение и каково оно.
Два неравенства
¦(a, b, c, …, k, x)>j(a, b, c, …, k, x) и (1)
z(a, b, c, …, k, x)>y(a, b, c, …, k, x) (2)
называются равносильными, если они имеют одинаковые общие решения при одном и том же множестве систем допустимых значений параметров.
§2. Алгоритм решения.
1. Находим область определения данного неравенства.
2. Сводим неравенство к уравнению.
3. Выражаем а как функцию от х.
4. В системе координат хОа строим графики функций а =¦ (х) для тех значений х, которые входят в область определения данного неравенства.
5. Находим множества точек, удовлетворяющих данному неравенству.
6. Исследуем влияние параметра на результат.
· найдём абсциссы точек пересечения графиков.
· зададим прямую а=соnst и будем сдвигать её от -¥ до+¥
7. Записываем ответ.
Это всего лишь один из алгоритмов решения неравенств с параметрами, с использованием системы координат хОа. Возможны и другие методы решения, с использованием стандартной системы координат хОy.
§3. Примеры
I. Для всех допустимых значений параметра а решить неравенство
![]()
Решение.
В области определения параметра а, определённого системой неравенств
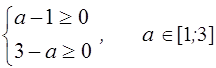
данное неравенство равносильно системе неравенств
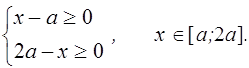
Если ![]() , то решения исходного неравенства заполняют отрезок
, то решения исходного неравенства заполняют отрезок ![]() .
.
Ответ: ![]() ,
, ![]() .
.
II. При каких значениях параметра а имеет решение система
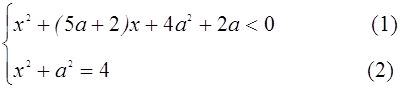
Решение.
Найдем корни трехчлена левой части неравенства –
![]() (*)
(*)
Прямые, заданные равенствами (*), разбивают координатную плоскость аОх на четыре области, в каждой из которых квадратный трехчлен
![]()
сохраняет постоянный знак. Уравнение (2) задает окружность радиуса 2 с центром в начале координат. Тогда решением исходной системы будет пересечение заштрихован
ной области с окружностью, где ![]() , а значения
, а значения ![]() и
и ![]() находятся из системы
находятся из системы
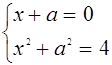
а значения ![]() и
и ![]() находятся из системы
находятся из системы
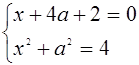
Решая эти системы, получаем, что
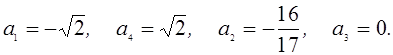
Ответ: ![]()
III. Решить неравенство ![]() на
на ![]() в зависимости от значений параметра а.
в зависимости от значений параметра а.
Решение.
Находим область допустимых значений – ![]()
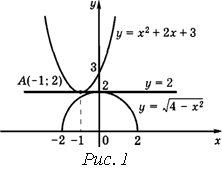
Построим график функции в системе координат хОу.
· при ![]() неравенство решений не имеет.
неравенство решений не имеет.
· при ![]() для
для ![]() решение х удовлетворяет соотношению
решение х удовлетворяет соотношению ![]() , где
, где ![]()
Ответ: Решения неравенства существуют при ![]()
![]() , где
, где ![]() , причем при
, причем при ![]() решения
решения ![]() ; при
; при ![]() решения
решения 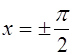 .
.
IV. Решить неравенство
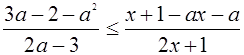
Решение.
Находим ОДЗ или линии разрыва (асимптоты)
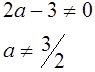
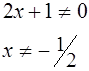
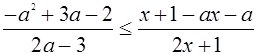
Найдем уравнения функций, графики которых нужно построить в ПСК; для чего перейдем к равенству :
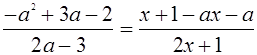
Разложим числитель на множители.
![]()
т. к. ![]() то
то
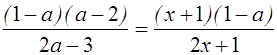
Разделим обе части равенства на ![]() при
при ![]() . Но
. Но ![]() является решением : левая часть уравнения равна правой части и равна нулю при
является решением : левая часть уравнения равна правой части и равна нулю при ![]() .
.
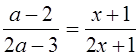
![]()
![]()
Похожие работы
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... ;[0; 1), тогда x – x +1 = 1; 1 = 1 Þ x — любое число из [0; 1). В) x Î[1; ¥), тогда x + x – 1 = 1; 2x = 2; x = 1 Î[1; ¥). Ответ: x Î[0; 1]. Основные методы решения рациональных уравнений. 1) Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по ...
... функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения. Ответ. . Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих ...
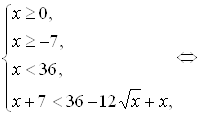
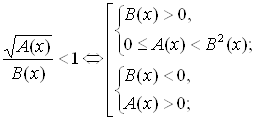
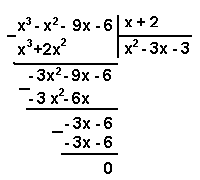


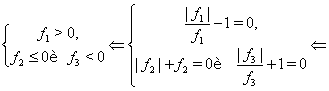
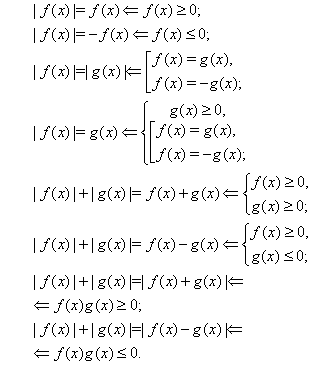
0 комментариев