Навигация
Ряд Фурье для функции с периодом 2l
6. Ряд Фурье для функции с периодом 2l.
Пусть функция ƒ(x) есть периодическая функция с периодом 2 l, вообще говоря, отличным от 2π. Разложим её в ряд Фурье.
Сделаем замену переменной по формуле
![]() х = lt / π.
х = lt / π.
Тогда функция ƒ(lt / π) будет периодичной функцией от t с периодом 2π. Её можно разложить в ряд Фурье на отрезке –π ≤ x ≤ π:
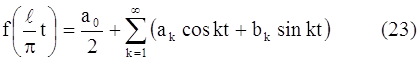
где (Пискунов, стр. 341 – дописывать не надо)
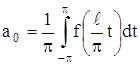
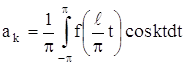
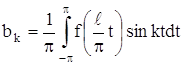
Возвратимся к старой переменной x:
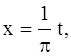
![]()
![]()
Тогда будем иметь:
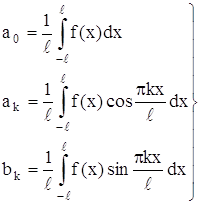 (24)
(24)
Формула (23) получит вид
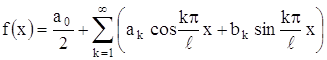 , (25)
, (25)
где коэффициенты a0, ak, bk вычисляются по формулам (24). Это и есть ряд Фурье для периодической функции с периодом 2 l.
Заметим, что все теоремы, которые имели место для рядов Фурье от периодических функций с периодом 2π, сохраняются и для рядов Фурье от периодических функций с каким-либо другим периодом 2 l.
Пример.
Разложить в ряд Фурье функцию ƒ(x) с периодом 2 l, которая на отрезке [-l , l] задается равенством ƒ(x) = | x |.
(Пискунов, стр.342, рис. 383)
Решение. Так как рассматриваемая функция – четная, то
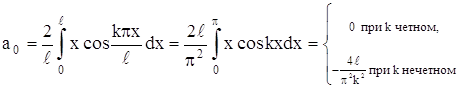
Следовательно, разложение имеет вид
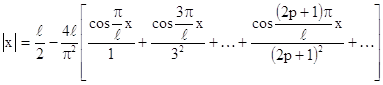
7. Разложение в ряд Фурье непериодической функции.
Пусть на некотором отрезке [a, b] задана кусочно монотонная функция ƒ(x). Покажем, что данную функцию ƒ(x) в точках её непрерывности можно представить в виде суммы ряда Фурье. Для этого рассмотрим произвольную периодическую кусочно монотонную функцию ƒ1(x) с периодом 2μ ≥ a - b, совпадающую с функцией ƒ(x) на отрезке [a, b]. Таким образом, дополнили определение функции ƒ(x).
Разложим функцию ƒ1(x) в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] (кроме точек разрыва) совпадает с заданной функцией ƒ(x), т. е. мы разложили функцию ƒ(x) в ряд Фурье на отрезке [a, b].
Рассмотрим следующий важный случай. Пусть функция ƒ(x) задана на отрезке [0, l]. Дополняя определение этой функции произвольным образом на отрезке [ l, 0 ] , мы можем разложить эту функцию в ряд Фурье. В частности, если мы дополним определение данной функции так, чтобы при - l ≤ х < 0 было ƒ(x) = ƒ(-x). В результате получится четная функция. В этом случае говорят, что функция ƒ(x) «продолжена четным образом». Эту функцию разлагают в ряд Фурье, которая содержит только косинусы. Таким образом, заданную на отрезке [0, l] функцию ƒ(x) мы разложили по косинусам.
Если мы продолжим определение функции ƒ(x) при - l ≤ х <0 так: ƒ(x) = -ƒ(-x), то получим нечетную функцию, которая разлагается по синусам. Таким образом, если на отрезке [0, l] задана некоторая кусочно монотонная функция ƒ(x), то её можно разложить в ряд Фурье как по косинусам, таки по синусам.
Комплексная форма ряда Фурье для функций с периодом 2π.
Пусть ƒ(x) – функция, удовлетворяющая условиям определения:
Пусть функция ƒ(x) с периодом 2π, имеющая на сегменте [-π, π] не более конечного числа точек разрыва и абсолютно интегрируема на этом сегменте (т. е. она интегрируема на любом сегменте).
Тогда пусть ряд (2) является рядом Фурье функции ƒ(x). Преобразуем общий член этого ряда с помощью формул Эйлера, выражающих косинус и синус через показательную функцию. Имеем:
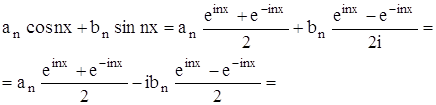
![]() ,
,
где ![]() .
.
Полагая ещё ![]() получим для частичных сумм ряда Фурье выражение
получим для частичных сумм ряда Фурье выражение
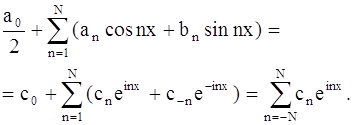
Для новых коэффициентов cn получаем формулу (учитывая формулы an и bn).
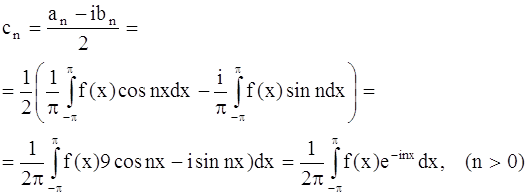
Непосредственно видно, что эта формула верна для n = 0 и для n < 0 (последнее видно, например, из того, что ![]() где
где ![]() обозначает число, сопряженное с).
обозначает число, сопряженное с).
По доказанному имеем в точках дифферуемциемоcти:
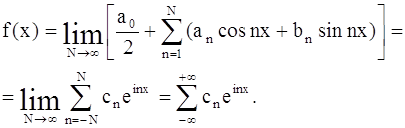
Итак, в точках дифференцируемости
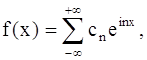 (26)
(26)
где
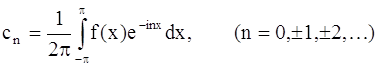
Правая часть формулы (26) представляет собой комплексную форму ряда Фурье для функции с периодом 2π.
Комплексная форма ряда Фурье для функции с любым периодом. (Романовский стр.33)
Пусть ƒ(x) – функция с периодом 2l, удовлетворяющая условиям , указанным в пункте 6. Тогда подстановка x= lt/ π приводит нас к функции ƒ(lt/ π) с периодом 2π. В силу предыдущего пункта в точках дифференцируемости имеем:
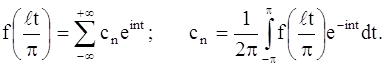
Переходя как в ряде, так и формулах для коэффициентов к старому переменному х и замечая, что t = π x / l, dt=(π / l)dx, получим в точках дифференцируемости:
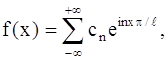 (27)
(27)
где
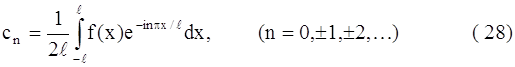 Правая часть формулы (27), где коэффициенты определяются равенствами (28), называется комплексной формой ряда Фурье для функции с периодом 2l.
Правая часть формулы (27), где коэффициенты определяются равенствами (28), называется комплексной формой ряда Фурье для функции с периодом 2l.
Основные типы уравнений математической физики.
Основными уравнениями математической физики называют (для случая функций двух независимых переменных) следующие дифференциальные уравнения с частными производными второго порядка.
1. Волновое уравнение:
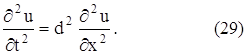
К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т. д. Это уравнение является простейшим уравнением гиперболического типа.
2. Уравнение теплопроводности или уравнение Фурье:
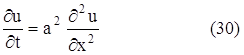
К исследованию этого уравнения приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде (например, фильтрации нефти и газа с подземных песчаниках), некоторые вопросы теории вероятностей и т. д. Это уравнение является простейшим уравнением параболического типа.
3. Уравнение Лапласа:
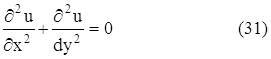
К исследованию этого уравнения приводит рассмотрение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики, диффузии и т. д. Это уравнение является простейшим уравнением эллиптического типа.
В уравнениях (29), (30) и (31) искомая функция u зависит от двух переменных. Рассматриваются также соответствующие уравнения и для функций с большим числом переменных. Так, волновое уравнение с тремя независимыми переменными имеет вид:
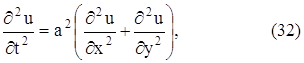
уравнение теплопроводности с тремя независимыми переменными имеет вид:
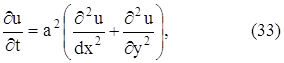
уравнение Лапласа с тремя неизвестными переменными имеет вид:
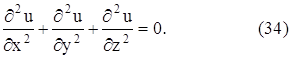
Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах.
В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени, направлены по касательной к её профилю. Пусть струна длины l в начальный момент напрвлена по отрезку оси Ох от 0 до l. Предположим, что концы струны закреплены в точках х = 0 и х = l. Если струну отклонить от её первоначального положения, а потом предоставить самой себе или, не отклоняя струны, предать в начальный момент её точкам некоторую скорость, или отклонить струну и придать её точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струны начнет колебаться. Задача заключается в определении закона движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ох и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией u (x, t), которая дает величину перемещения точки струны с абсциссой х в момент времени t.

(Н.С. Пискунов стр. 245, рис. 371)
Так как мы рассматриваем малые отклонения струны в плоскости (x, u ), то будем предполагать, что длина элемента струны М1М2 равняется её проекции на ось Ох, т. е. М1М2 = х2 – х1. Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
Рассмотрим элемент струны ММ′. На концах этого элемента, по касательным к струне, действуют силы Т.
(Н.С. Пискунов стр. 246, рис. 372)
Пусть касательные образуют с осью Ох углы φ и φ + ∆φ. Тогда проекция на ось Ou сил, действующих на элемент ММ′, будет равна T· sin (φ + ∆φ) – sin φ . Так как угол φ мал, то можно положить tg φ ≈ sin φ, мы будем иметь:
T sin (φ + ∆φ) – T sin φ ≈ T tg (φ + ∆φ) – T tg φ =
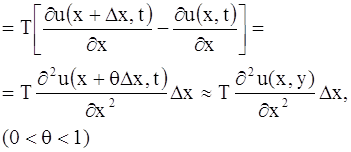
(здесь мы применили теорему Лагранжа к выражению, стоящего в квадратных скобках).
Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть ρ – линейная плотность струны. Тогда масса элемента струны будет ρ ∆х. Ускорение элемента равно ∂2u / ∂t2. Следовательно, по принципу Даламбера будем иметь:
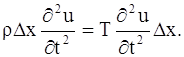
Сокращая на ∆х и обозначая a2 = T/ ρ, получаем уравнение движения
![]()
Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения движения струны одного уравнения (35) недостаточно. Искомая функция u(x, t) должна удовлетворять ещё граничным условиям, указывающих, что делается на концах струны (х = 0 и х = ℓ), и начальным условиям, описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.
Пусть, например, как мы предполагали, концы струны при х = 0 и х = ℓ неподвижны. Тогда при любом t должны выполняться равенства:
u (0, t) = 0, (36)
u (ℓ, t) = 0. (36,)
Эти равенства являются граничными условиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией ƒ(x). Таким образом, должно быть
u (x, 0) = u |t = 0 = ƒ(x). (37)
Далее в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией φ(х):

Условия (101,) и (101, ,) являются начальными условиями.
Замечание. В частности, может быть, ƒ(x) ≡ 0 или φ(x) ≡ 0. Если же ƒ(x) ≡ 0 и φ(x) ≡ 0, то струна будет находиться в покое, следовательно, u (x, t) ≡ 0.
Как указывалось выше, к уравнению (30) приводит и задача об электрических колебаниях в проводах. Покажем это. Электрический ток в проводе характеризуется величиной ί(x, t) и напряжением υ(x, t), которые зависят от координаты х точки провода и от времени t. Рассматривая элемент провода ∆х, можем написать, что падение напряжения на элементе ∆х равно
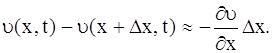
Это падение напряжения складывается из омического, равного ίR∆x, и индуктивного , равного (∂ ί /∂ t )L∆x. Итак,
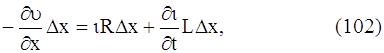
где R и L - сопротивление и коэффициент самоиндукции, рассчитанный на единицу длины провода. Знак минус взят потому, что ток течет в направлении, обратном возрастанию υ. Сокращая на ∆х, получаем уравнение
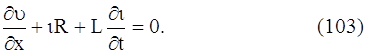
Далее, разность токов, выходящих из элемента ∆х и выходящего из него время ∆t, будет
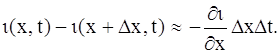
Она расходуется на зарядку элемента, равную C∆x (∂υ /∂t) ∆t, и на утечку через боковую поверхность провода вследствие несовершенства изоляции, равную Аυ∆х∆t (здесь А – коэффициент утечки). Приравнивая эти выражения и сокращая на ∆x∆t, получим уравнение:
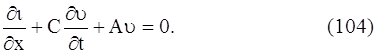
Уравнения (103) и (104) принято называть телеграфными уравнениями.
Из системы уравнений (103) и (104) можно получить уравнение, содержащую только искомую функцию ί(x, t), и уравнение, содержащее только искомую функцию υ (x, t). Продифференцируем члены уравнения (104) по х; члены уравнения (103) продифференцируем по t и умножим их на С. Произведя вычитание, получим:
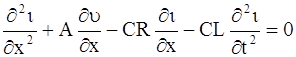
Подставляя в последнее уравнение выражение (∂υ /∂х) из уравнения (103), получим:
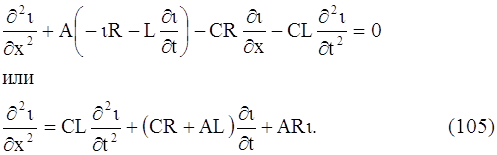
Аналогичным образом получается уравнение для определения υ(x, t):
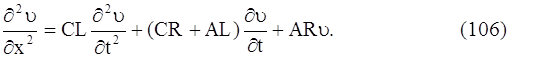
Если можно пренебречь утечкой через изоляцию (А = 0) и сопротивлением (R = 0), то уравнения (105) и (106) переходят в волновые уравнения:
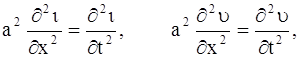
где обозначено: a2 = 1/CL. Исходя из физических условий, формулируются граничные и начальные условия задачи.
Решение уравнения колебаний струны методом разделения переменных (методом Фурье).
Метод разделения переменных (или метод Фурье) является типичным для решения многих задач математической физики. Пусть требуется найти решение уравнения

удовлетворяющее краевым условиям:
u (0, t) = 0, (108)
u (ℓ, t) = 0, (109)
u (x, 0) = ƒ(x), (110)

Будем искать (не равное тождественно нулю) частное решения уравнения (107), удовлетворяющее граничным условиям (108) и (109), в виде произведения двух функций X(x) и T(t), из которых первая зависит только от х, вторая только от t:
u (x, t) = X (x) T (t). (112)
Подставляя в уравнение (107), получаем:
X (x) T′′(t) = a2 X′′(x) T(t).
Разделив члены равенства на a2 XT![]()

В левой части этого равенства стоит функция, которая не зависит от х, слева – функция, не зависящая от t. Равенство (113) возможно только в том случае, когда левая и правая части не зависят ни от х, ни от t, т. е. равны постоянному числу. Обозначим его через – λ, где λ > 0 ( позднее будет рассмотрен случай λ < 0). Итак,
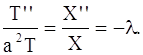
Из этих равенств получаем два уравнения:
X′′ + λX = 0, (114)
T′′ + a2 λT = 0. (115)
Общие решения этих уравнений будут:
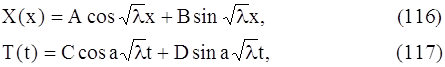
где A, B, C, D – произвольные постоянные.
Подставляя выражения X(x) и T(t) в равенство (112), получим:
![]()
Подберем теперь постоянные А и В так, чтобы удовлетворялись условия (108) и (109). Так как T (t) тождественно неравна нулю (в противном случае u (x, t) ≡ 0, что противоречит поставленному условию),то функция X (x) должна удовлетворять условиям (108)
и (109), т. е. должно быть Х (0) =0, Х (ℓ) = 0. Подставляя значения х=0 и х = ℓ в равенство (116), на основании (108) и (109) получаем:
0 = А · 1 + В · 0,
![]()
Из первого уравнения находим А = 0. Из второго следует:
![]()
В ≠ 0, так как в противном случае было бы Х ≡ 0 и u ≡ 0, что противоречит условию. Следовательно, должно быть
![]()
откуда
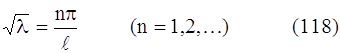
(мы не берем значение n = 0, так как в этом случае было бы Х ≡ 0 и u ≡ 0). Итак, мы получили:

Найденные значения λ называются собственными значениями для данной краевой задачи. Соответствующие им функции Х (х) называются собственными функциями.
Замечание. Если бы мы знали вместо – λ выражение + λ = k2, то уравнение (114) приняло бы вид
Х′′- k2Х = 0.
Общее решение этого уравнения:
Х = Аekx + Be -kx .
Отличное от нуля решение в такой форме не может удовлетворять граничным условиям (108) и (109).
Зная λ1/2, мы пользуясь равенством (117) , можем написать:
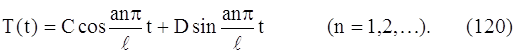
Для каждого значения n, следовательно, для каждого λ, выражения (119) и (120) подставляем в равенство (112)и получаем решение уравнения (107), удовлетворяющее граничным условиям (108) и (109). Это решение обозначим un (x, t):
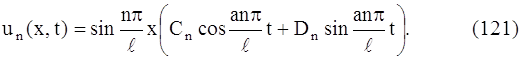
Для каждого значения n мы можем брать свои постоянные C и D и потому пишем Cn и Dn (постоянная В включена в Cn и Dn). Так как уравнение (107) линейное и однородное, то сумма решений также является решением, и потому функция, представленная рядом
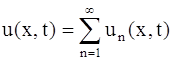
или
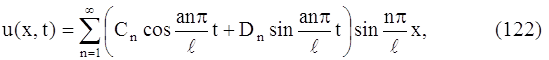 также будет решением дифференциального уравнения (107), которое будет удовлетворять граничным условиям (108) и (109). Очевидно, ряд (122) будет решением уравнения (107) только в том случае, если коэффициенты Cn и Dn таковы, что этот ряд сходится в ряды получающиеся после двукратного почленного дифференцирования по х и по t.
также будет решением дифференциального уравнения (107), которое будет удовлетворять граничным условиям (108) и (109). Очевидно, ряд (122) будет решением уравнения (107) только в том случае, если коэффициенты Cn и Dn таковы, что этот ряд сходится в ряды получающиеся после двукратного почленного дифференцирования по х и по t.
Решение (122) должно еще удовлетворять начальным условиям (110) и (111). Этого мы будем добиваться путем подбора постоянных Cn и Dn. Подставляя в равенство (122) t = 0, получим :
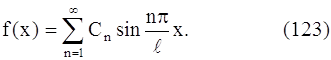
Если функция ƒ(x) такова, что в интервале (0, ℓ) ее можно разложить в ряд Фурье, то условие (123) будет выполняться, если положить
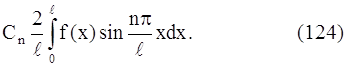
Далее, дифференцируем члены равенства (122) по t и подставляем t = 0. Из условия (111) получается равенство
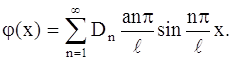
Определяем коэффициенты Фурье этого ряда:
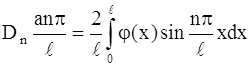
или
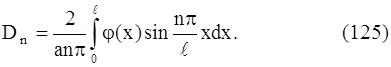
Итак, мы доказали, что ряд (122), где коэффициенты Cn и Dn определены по формулам (124) и (125), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t), которая является решением уравнения (107) и удовлетворяет граничным и начальным условиям (108) – (111).
Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (122) представляет собой решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция ƒ(x) должна быть дважды дифференцируемой, а функция φ(x) – один раз дифференцируемой.
Уравнение распространения тепла в стержне. Формулировка краевой задачи.
Рассмотрим однородный стержень длины ℓ. Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.
Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = , а другой – с точкой х = ℓ.
![]()
Пискунов стр 252, рис. 373
Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.
Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 = ∆х). Количество тепла, прошедшего через сечение с абсциссой х1 за время ∆t, будет равно
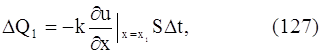
то же самое с абсциссой х2:
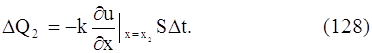
Приток ∆Q1 - ∆Q2 в элемент стержня за время ∆t будет равняться:
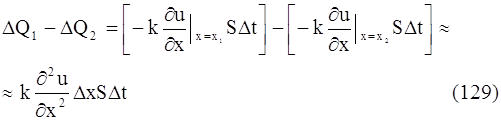
Этот приток тепла за время ∆t затратился на повышение температуры элемента стержня на величину ∆u:
![]()
или
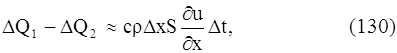
где с – теплоемкость вещества стержня, ρ – плотность вещества стержня (ρ∆xS – масса элемента стержня).
Приравнивая выражения (129) и (130) одного и того же количества тепла ∆Q1 - ∆Q2, получим:![]()
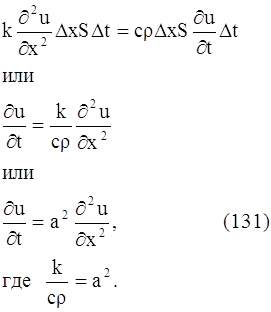
Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.
Чтобы решение уравнения (131) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (131) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для 0 ≤ t ≤ T, следующие:
u (x, 0) = φ(x), (132)
u (0, t) = ψ1(t), (133)
u (ℓ, t) = ψ2(t). (134)
Физическое условие (132) (начальное условие) соответствует тому, что при t = 0 в разных сечениях стержня задана температура, равная φ(x). Условия (133) и (134) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х = ℓ поддерживается температура, равная ψ1(t) и ψ2(t) соответственно.
Доказывается, что уравнение (131) имеет единственное решение в области 0 ≤ х ≤ ℓ, 0 ≤ t ≤ T , удовлетворяющее условиям (132) – (134).
Распространение тепла в пространстве.
Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u(x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку ∆s, т. е. количество тепла, протекающего за единицу времени, определяется формулой (аналогично формуле (126))
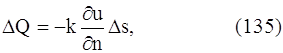
где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке ∆s в направлении движения тепла. Таким образом, можем записать:
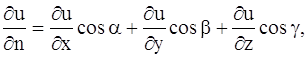
где cos α, cos β, cos γ – направляющие косинусы вектора n, или
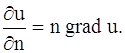
Подставляя выражение ![]() в формулу (135), получаем:
в формулу (135), получаем:
∆Q = -k n grad u ∆s.
Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:
∆Q∆t = -k n grad u ∆t ∆s.
Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:
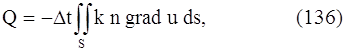
где n – единичный вектор, направленный по внешней нормали к поверхности S. Очевидно, что формула (136) дает количество тепла, поступающего в объем V (или уходящего из объема V) за время ∆t. Количество тепла, поступившего в объем V, идет на повышение температуры вещества этого объема.
Рассмотрим элементарный объем ∆υ. Пусть за время ∆t его температура поднялась на ∆u. Очевидно, что количество тепла, затраченное на это повышение температуры элемента ∆υ, будет равно
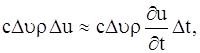
где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время ∆t, будет
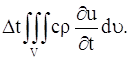
Но это есть тепло, поступающее в объем V за время ∆t; оно определено формулой (136) . Таким образом, имеет место равенство
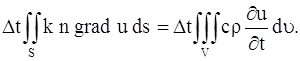
Сокращая на ∆t, получаем:
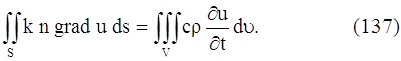
Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, σ – замкнутая поверхность)
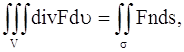
полагая F = k grad u:
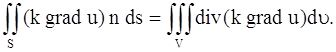
Заменяя двойной интеграл, стоящий в левой части равенства (137), тройным интегралом, получим:
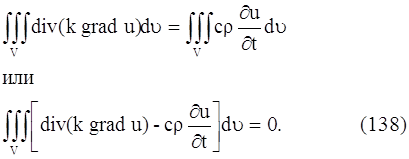
Применив теорему о среднем к тройному интегралу, стоящего слева, получим :
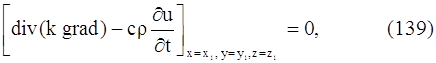
где P(x, y, z) – некоторая точка объема V.
Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (138) непрерывна, то равенство (139) будет выполняться в каждой точке пространства. Итак,
![]()
Но
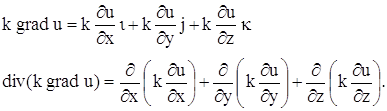
Подставляя в уравнение (140), получаем:
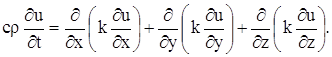
Если k – постоянное, то
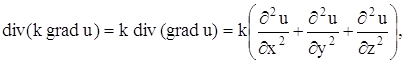
и уравнение (140) в этом случае дает:
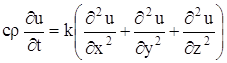
или, положив 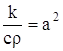
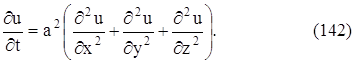
Коротко уравнение (142) записывается так:
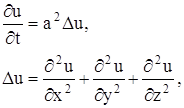
где ![]() ∆u – оператор Лапласа. Уравнение (142) и есть уравнение теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые условия.
∆u – оператор Лапласа. Уравнение (142) и есть уравнение теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые условия.
Пусть имеем тело Ω, поверхность которого σ. В этом теле рассматривается процесс распространения тепла. В начальный момент температура тела задана. Это соответствует тому, что известно значение решения при t = 0 – начальное условие:
u(x, y, z, 0) = φ (x, y, z). (143)
Кроме того, должна быть известна температура в любой точке М поверхности σ тела в любой момент времени t – граничное условие:
u (М, t) = ψ (М, t). (144)
(Возможны и другие граничные условия.)
Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:
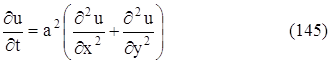
- уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (143) и (144), формулируются так:
u (x, y, 0) = φ (x, y),
u(М, t) = ψ (М, t),
где φ и ψ – заданные функции, М – точка границы С.
Если же функция u не зависит ни от z, ни от y, то получаем уравнение
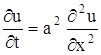
- уравнение распространения тепла в стержне.
2π, ƒ(x), φ, φ(x) ,[-π, π], (λ, λ +2π), ψ(x), ·, ℓ, l, < x ≤, | x |,α, β,[a, b], σ, u (x, t), М1М2 ,φ +, ∆φ ,≈, ρ, ∆, ∂, ≡, ι, ί, υ, ′, ≠, κ, k, s, u(x, y, z, t), Ωσ
Заключение
В этой дипломной работе приведены лишь немногие примеры того как ряды Фурье позволяют решить важные задачи математической физики. Например, некоторыми из них являются задачи на распространения тепла в стержне или колебания струны. Приведены примеры нахождения периодических решений линейных дифференциальных уравнений с помощью рядов Фурье. На небольшом количестве страниц изложен материал, содержащий основные факты теории рядов Фурье.
Работа начинается с представления функции в виде тригонометрического ряда, который и является при подставлении в него соответствующих коэффициентов (коэффициентов Фурье) рядом Фурье. Далее рассматриваются некоторые признаки сходимости рядов Фурье, вывод коэффициентов Фурье и их оценка. Представлена комплексная форма рядов Фурье. Рассмотрены примеры применений преобразований Фурье и метода Фурье (метода разделения переменных).
Так как теория тригонометрических рядов (рядов Фурье) в настоящее время достаточно велика по своему содержанию и объему, то естественно, что здесь не мог быть исчерпан весь материал.
В заключение хотелось бы отметить, что о Фурье мы прежде всего вспоминаем как об авторе “Аналитической теории теплоты” (1822 г.). В силу общности метода эта книга стала источником всех современных методов математической физики, относящихся к интегрированию уравнений в частных производных при заданных граничных условиях.
Литература:
1. Н.С. Пискунов „Дифференциальное и интегральное исчисления”, Москва, „Наука”, 1972 г.
2. И.М. Уваренков, М.З. Маллер „Курс математического анализа”, Москва, „Просвещение”, 1976 г.
3. В.С. Шипачев „Высшая математика”, Москва, „Высшая школа”, 1990г.
4. Г.Е. Шилов „Математический анализ функции одного переменного”, Москва, „Наука”, 1970 г.
5. Я.С. Бугров, С.М. Никольский „Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного”, Москва, „Наука”, 1989 г.
6. В.А. Подольский, А.М. Суходский „Сборник задач по математике для техников-программистов”, Москва, „Высшая школа”, 1978 г.
7. Г.М. Фихтенгольц „Курс дифференциального и интегрального исчисления”, том III, Москва, „Наука”, 1969г.
8. В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов „Краткий курс высшей математики”, том2, Москва, „Высшая школа”, 1978г.
Похожие работы
... затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…). Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании. Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными ...
... . Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10). Глава 3. Операционное исчисление § 14. Преобразование Лапласа Понятие оригинала. Кусочно-непрерывная функция называется оригиналом, если выполняются следующие условия: 1) для всех ...
... Таким образом, имеется следующая задача : На основе существующих алгоритмов проанализировать возможность их применения как к последовательной обработке сигналов в реальном времени, так и к блочной обработке и оценить качество получаемых результатов . Критериями «качества» оценки спектральной плотности мощности в общем случае являются смещение этой оценки и ее дисперсия. Однако аналитическое ...
... , можно сделать вывод о том, что показатель естественного прироста населения наиболее точно прогнозируется рядом Фурье. Заключение В ходе работы было проведено моделирование и прогнозирование естественного прироста населения в РФ. Исследование было проведено с помощью следующих моделей: · Аддитивная модель; · Мультипликативная модель; · Одномерный анализ Фурье; · Регрессионная модель с ...
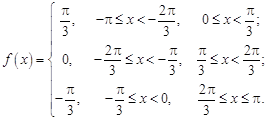
0 комментариев