Навигация
Вычисление оценки Писаренко
1.4.2 Вычисление оценки Писаренко
При разработке алгоритмов вычисления оценки Писаренко можно столкнуться с дискретной спектральной основой
Для такой основы основная задача /4.4/ может быть переписана в виде линейное программы стандартного вида
(4.11з)
так что для
(4.11b)
с N переменными и 2М ограничениями. Минимум равен и достигается для . Основная теорема линейного программирования 18 эквивалентна теореме представления в этом случае. При условии, что для этой линейной программы существует решение, как показано в предыдущем разделе, основная теорема гарантирует решение, в котором не более, чем 2М из не равны нулю, так называемое, базовое решение.
Двойственная линейная программа [l5]
(4.12з)
так что для
(4.12b)
эквивалентная двойственной задаче /4.9/ для дискретной спектральной основы, где ограничение
(4.13)
было использовано для исключения и где . Её минимум равен и достигается при .
Основная задача может быть решена при использовании симплекс-метода [18]. Применение симплекс-метода к основной задаче приводит в результате к существенно тому же результату /вычислительному алгоритму/, что и применение, /одинарного/ метода замены к двойственной задаче [19]. Применив соответствующий метод для избежания зацикливания [20], может быть получен алгоритм, который гарантирует сходимость к оптимальному решению за конечное число шагов, хотя его воплощения обычно были медленными .
Задача чебышевской аппроксимации связана с вычислением оценки Писаренко; она может быть сформулирована, как минимизация линейного функционала на выпуклом пространстве, определенном ограничениями типа линейных неравенств [l6]. Она также решалась с использованием симплекс-метода /одинарная замена/. Однако для частной задачи чебышевской аппроксимации непрерывных функций полиномами с одной переменной существует вычислительный метод, который значительно быстрее симплекс-метода, это метод многократной замены Ремеза. Хотя были сделаны попытки распространить этот метод на более общие задачи [21], появившиеся в результате алгоритмы не достаточно хорошо понятны; в частности, не доказана их сходимость.
И наконец, задачи недискретной оптимизации, включенные в вычисление оценки Писаренко, /4.4/ к /4.9/, являются видом, известным, как полубесконечные программы. Как теоретические, так и вычислительные аспекты таких программ рассматриваются в сборнике статей, изданных Геттичем [22].
Резюме
Эта статья связана с тем, что вероятно является наиболее простой и интересной задачей в обработке антенных решеток; оценкой спектра мощности с известной основой при условии, что даны некоторые выборки его корреляционной функции. Хотя и простая, эта задача сохраняет несколько черт, которые являются общими для многих задач обработки решеток: многомерные спектры, корреляционные выборки с неравномерными отчетами и произвольные спектральные основы.
Исследование спектральных оценок, согласованных с корреляцией привели к задаче продолжимости. Были даны две характеристики продолжаемости ста задача, для случая временных последовательностей, известна как задача тригонометрических моментов и ее решение включает рассмотрение положительной определенности корреляционных выборок. Положительная определенность может поэтому рассматриваться как специальный случай продолжимости.
Базируясь на теоретической основе, разработанной при решении задачи продолжаемости, метод Писаренко был распространен со случая временных последовательностей на задачу обработки решетки. Было показано, что метод Писаренко тесно .связан с задачек продолжимости. Было показано, что вычисление оценки Писаренко включает решение линейной задачи оптимизации. Было показало, что решение этой задачи не является единственным в общем случае, хотя оно единственно для случая временной последовательности, где задача линейном оптимизации сводится к задача собственных значений.
Хотя рассмотренная в этой статье задача спектральной оценки была разработала для обработки решетки, теоретическая структура и результирующие алгоритмы должна быть полезными в других многомерных задачах, например, обработке изображений.
2.1 ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ДЛЯ ОТКРЫТОГО РЕЗОНАТОРА С ОСЕСИММЕТРИЧНЫМ ДИСКОМ
В § 9.3 было получено интегральное уравнение (9.39) для резонатора с диэлектрическим телом в виде шара. Такая форма диэлектрика хороша для анализа, но неудобна для практики.
Обычно приходится иметь дело с диэлектрическими образцами более сложной формы, в частности с диэлектрическим диском. В такой ситуации получить аналитическое выражение для ядра не удается, однако это не является препятствием для нахождения решения задачи.
Действительно, ядро уравнения для резонатора с шаром (9.39) — это сумма ядра для пустого резонатора и дополнительного члена, представляющего собой поле, рассеянное шаром.
Запишем уравнение для резонатора с диском в аналогичном виде, поскольку физическая картина явлении одна и та же:
(9.45)
Здесь - ядро пустого резонатора; Т — ядро, связанное с рассеянием на диэлектрическом образце. Обсудим, что в сущности делается при решении уравнения (9.39) методом Галеркина. Для определенности будем считать, что в качестве базисных и весовых (см. приложение 2) взяты собственные функции резонатора без шара, которые обозначим и будем считать ортонормированными.
С первым слагаемым ядра все ясно, базисные функции являются его собственными, и действие интегрального оператора с таким ядром эквивалентно умножению на постоянную, являющуюся собственным значением пустого резонатора:
(9.46)
Интегральный оператор со вторым слагаемым ядра представляет собой магнитное поле тока на зеркалах, рассеянное шаром. Плотность тока задается в виде , а рассеянное поле рассчитывается на поверхности зеркала. При решении (9.39) расчет рассеянного шаром поля проводится аналитически. Однако ту же процедуру можно произвести численно, и тогда ограничения на формулу диэлектрического образца в значительной степени снимаются.
Для расчета рассеянного поля будем применять интегральное уравнение (3.85). Диэлектрический образец может быть произвольным телом вращения, в частности диском.
После этих общих соображений рассмотрим процедуру решения (9.45) последовательно. Функция U(x) ищется в виде
(9.47)
В соответствии с методом Галеркина (см. приложение 2) подставляем (9.47) в (9.45), затем умножаем на и повторно интегрируем по образующей зеркала. С учетом ортонормированности базисных функций имеет однородную СЛАУ
(9.48)
где - собственные числа уравнения невозмущенного резонатора [см. (9.46)].
Элементы матрицы СЛАУ выражаются интегралами
(9.49)
Последнюю формулу надо понимать как символическую. Она эквивалентна процедуре расчета рассеянного поля, описанной выше. Остановимся на ней подробнее.
Вначале необходимо найти поле на поверхности диэлектрического тела, созданное током вида на зеркалах. Это можно было бы сделать с помощью (3.8), (3.9), однако есть более простой путь, если ограничиться рассмотрением тел небольших, на порядок меньших диаметра зеркал. Тогда можно воспользоваться приближенным выражением для поля в резонаторе, соответствующим приближенным функциям токов на зеркалах. На рис. 9.6 представлены графики распределения токов на зеркалах, соответствующие низшему типу колебаний и колебанию, имеющему вариацию по радиусу . Резонатор конфокальный с параметром . Вблизи оси плотность тока, описываемая гиперсфероидальными функциями (кривые 1), практически не отличаются от экспоненциальной функции, умноженной на полиномы Лагерра (кривые 2), т. е. от гауссова пучка [68]. Радиальное распределение отличается только масштабом по радиусу.
Таким образом, будем описывать поле в резонаторе вблизи его центра приближенным .выражением в виде гауссова пучка
(9.50)
где
;
R - радиус кривизны волнового фронта; W — радиус «освещенного пятна» в пучке. Последняя величина определяется как радиус, на
Рис. 9.6. Сравнение точных и приближенных кривых для гиперсфероидальных функций:
1 - точные, 2 - приближенные кривые
котором интенсивность пучка спадает в е раз по отношению к центру пучка. Характерной величиной для каждого пучка является наименьший радиус «пятна» . Применительно к резонатору - это радиус «пятна» в центре, который связан с длиной резонатора 1:
(9.51)
1 Как и ранее, все длины предполагаются умноженными на волновое число, которое здесь соответствует действительной части собственной частоты невозмущенного резонатора.
Величины W и R медленно меняются вдоль резонатора:
(9.52)
(9.53)
В центре резонатора Естественно в резонаторе существуют не один, а два встречных гауссовых пучка, и вблизи центра поле основной моды в приближении гауссова пучка имеет вид
(9.54)
На зеркале для конфокальной геометрии резонатора в соответствии с (9.51)—(9.53) , и распределение тока имеет вид1
(9.55);
Для следующего колебания «1, 0, q» поле в центре резонатора представляется формулой
(9.56)
и на зеркалах
(9.57)
Таким образом, поле в резонаторе без образца, соответствующее различным модам, в приближении гауссова пучка нетрудно записать. Оно играет роль первичного поля для задачи возбуждения диэлектрического образца.
Вычисляем эквивалентные токи на поверхности диэлектрика в предположении, что основная поляризация поля . В обозначениях § 3.3 имеем:
1 Напомним, что в открытых резонаторах с круглыми зеркалами принята следующая индексация мод : первый индекс - число вариаций по R, второй - число вариаций по , а третий - число вариаций по
(9.58)
Теперь необходимо возвратиться к азимутальным гармоникам вида , поскольку ЭВМ — программы для диэлектрических тел вращения сделаны применительно к ним. Первичные токи представляют собой сумму первой и минус первой гармоник. Каждую из них можно выделить, используя формулу Эйлера. В результате решения задачи возбуждения диэлектрического тела, а конкретно диска, получаем значения эквивалентных токов в дискретных и достаточно часто расположенных точках образующей. Зависимость от этих токов известная. Если объединить токи первой и минус первой гармоник, она будет такой же, как и у первичных токов (9.58).
Следующий этап — вычисление рассеянных диском полей на зеркалах. Для этого используются формулы (3.8), (3.9). Выра жения для элементов тензорной функции Грина следует упрос тить, как и при выводе уравнений (9.5)—(9.8), т. е. положить , а для функции использовать асимптотическую формулу (9.22). Последняя содержит множитель, учитывающий набег фазы на половине размера резонатора (расстояние от образца до одного из зеркал). Такой же набег фаз имеется в первичном для диэлектрического образца поле. Этот сдвиг присутствует также в (9.56) и (9.57). Все это позволяет вынести за знак интеграла множитель , такой же, как и из основного ядра. Этот множитель, как и ранее, дает основную частотную зависимость. Ядра без него от частоты зависят слабо, и в них частота полагается равной действительной части собственной частоты пустого генератора.
Теперь уже можно вычислить элементы матрицы (9.48). Для определения элемента берется рассеянное поле, возбужденное нулевой модой пустого резонатора, т. е. , затем оно в соответствии с (9.49) домножается на (9.55) и интегрируется. При этом необходимо помнить, что базисные функции предполагались нормированными. Поэтому функцию (9.55) необходимо предварительно пронормировать. В силу осевой симметрии системы поверхностный интеграл (9.49) можно представить в координатах вращения. Интеграл по берется аналитическим, а по радиальной координате - численно. Остальные элементы отыскиваются точно так же.
Далее решается задача на собственные значения, а затем с помощью формул (9.40) и (9.41) находятся изменения добротности и сдвиг частоты.
Похожие работы
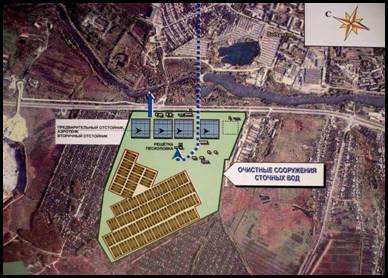
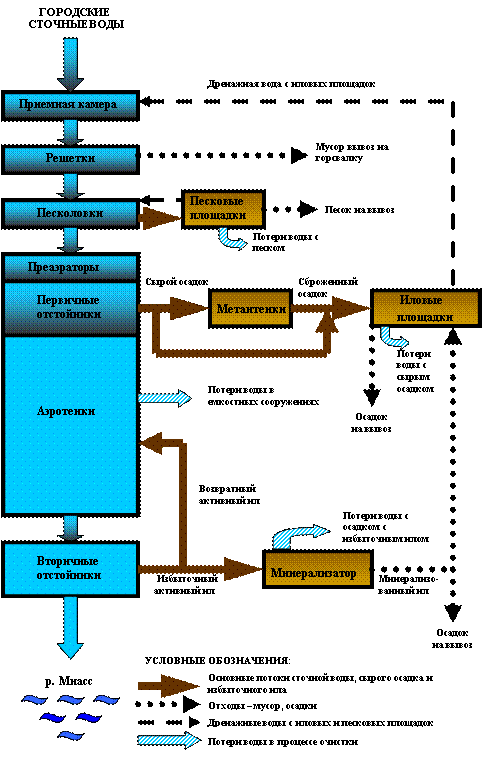
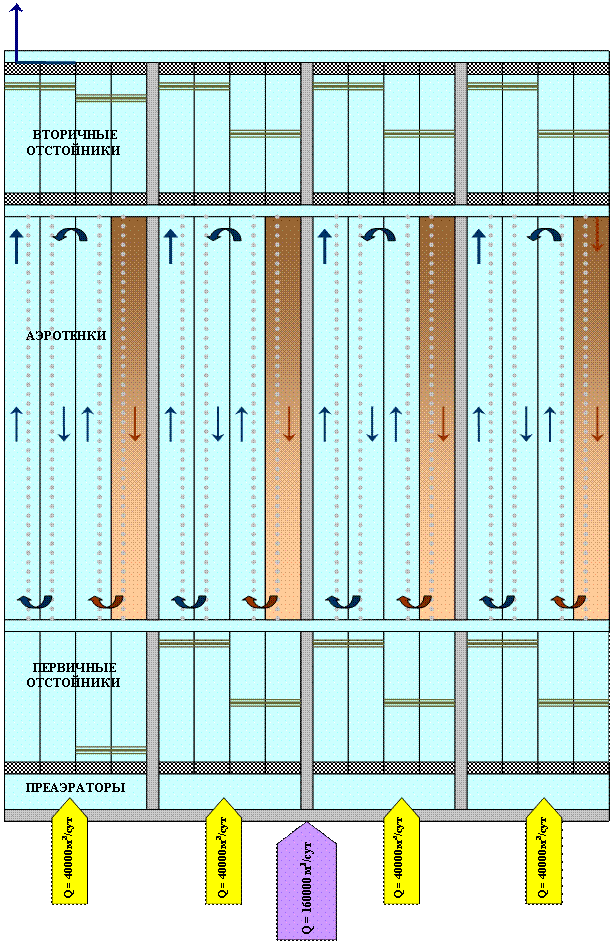
... быть использована в качестве присадочного материала при подготовке осадка к обезвоживанию. Это позволяет снизить расход химических реагентов. Проектирование новых и реконструкцию существующих комплексов для обработки осадков на очистных станциях и установках рекомендуется выполнять применительно к унифицированным производительностям очистных установок и станций, а также к местным условиям и ...
... педагогические условия и приемы, обеспечивающие их коррекцию путем переструктурирования мотивационной сферы личности и расширения у студентов взаимосвязей учебно-профессиональных и физкультурных мотивов. Существенной особенностью данного исследования было использование метода репертуарных решеток, что позволило изучать у студентов мотивы и их структуры, максимально приближенные к независимой от ...
... (в фазе трех-пяти листьев у сорняков). При использовании гербицидов количество механических операций можно сократить. Обработку гербицидами начинают за З-4 дня до появления всходов. В интенсивной технологии возделывания картофеля важное мecтo занимает окучивание. Задача окучивания – не только удаление сорняков, рыхление почвы вокруг растений и создание лучших условий для клубнеобразования, но ...
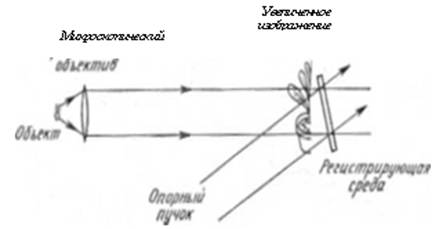
... перемещений лежит от долей микрона до нескольких миллиметров. Голографическая интерферометрия и спекл-интерферометрия являются двумя широкими областями, используемыми для обнаружения перемещений методами когерентной оптики. Кратко рассмотрим каждую из них, чтобы иметь возможность сравнивать их между собой. Голографическая интерферометрия основывается на достоинстве голографии (т. е. возможности ...


0 комментариев