Навигация
МЕТОД СВЧ КОНТРОЛЯ ПАРАМЕТРОВ ПОЛИМЕРОВ
3 МЕТОД СВЧ КОНТРОЛЯ ПАРАМЕТРОВ ПОЛИМЕРОВ
Для контроля технологических параметров полимеров (качества смещения, определение включений, вязкости) находят применение радиоволновые метода СВЧ. Рассмотрим метод, который характеризуется определением объёмной эффективной площади рассеяния ( ЭПР ).
ЭПР это площадь поперечного сечения некоторого фиктивного тела, которое рассеивает электромагнитную в одну, ЭПР существенно зависит от формы м ориентации тела, от его материала ЭПР, разрешаемого объема заполненного частицами ( элементарными отражателями), выражается произведением . Так для реальных полимерных материалов требуется знать распределение частиц во размерам размеры частиц в единице объёма распределены по групп и в 1-й группе содержится частиц с аффективной площадью рассеяния , то удельная объёмная ЭПР
(1)
ЭПР одной сферической частицы, диаметр которой много меньше длины волны, определяется формулой
(2)
Коэффициент , выраженный через комплексный показатель преломления изменяется от для частиц наполнителя.
Практически для большинства объектов полимерных структур
с наполнителем удельную ЭПР можно выразить формулой
(3)
Множитель
(4)
можно назвать отражаемостью, которая зависит от концентрации и размера частиц в разрезаемом элементе.
Изменение базы волны ври отражении можно определить из отпадения напряженностей поля падающей () и отраженной () волн:
, (5)
Модель этой комплексной величины , имеющей размерность длины, определяет интенсивность отражения. Аргумент указывает на изменение фазы волны при отражении.
Если рассматривать прием и передачу на одну и туже антенну, т.е. одинаковой ( согласованной) поляризацией, умножим выражение на комплексно сопряженную величину
,
В результате получаем
Это означает, что если эффективная площадь - площадь квадрата, то модель эффективной длины - это сторона того квадрата; - - точное расстояние до источника, определяющего фазу колебаний .
Для поляризованного колебания напряженность регулярного электромагнитного поля выражается вектором , который вращается с угловой скоростью и конец которого описывает эллипс в плоскости перпендикулярной направлению распространения. Если распространение происходит в направлении оси прямоугольной системы координат , определяемой ортами ,то эллиптически поляризованная волна выражается составляющими к полностью описывается четырьмя параметрами: амплитуда , и фазами y. Однако не все эти параметры характеризуют поляризацию. Одинаково поляризованными называются волны, у которых эллипсы поляризации подобны и одинаково ориентированы. Абсолютное значение амплитуд, влияющие лишь на размеры эллипсов поляризации, начальная фаза , одинаковая для обеих составляющих, ив является поляризационными характеристиками.
Следовательно состояние поляризации плоской волны можно полностью определить двумя параметрами (рис.1 ).
Рис.1 Эллиптически поляризованная плоская волна
В качестве таких параметров могут служить отношение амплитуд и сдвиг фаз y ортогональных составляющих; отношение амплитуд часто заменяют углом . Поляризацию можно также задать величинами, непосредственно характеризующими форму и ориентацию эллипса: отношение главных осей эллипса углом и углом наклона главной оси (рис.1).
Система координат , в которой представлено поляризованное колебание, может быть задана парой единичных взаимно перпендикулярных векторов , . Такие ортогональные векторы - орты - называются поляризованным базисом.
В поляризованном базисе ( , ) вектор можно представить выражением
где , и , - модули и фазы комплексных амплитуд, составляющих напряженности электрического поля соответственно. Если , то поляризация линейна, при она эллиптическая. При круговой поляризации амплитуды составляющих одинаковы, а фазы сдвинуты на 90°.
Поляризационные преобразования при отражении можно представить уравнениями
связывающими ортогональные составляющие напряженности ноля падающей () и отраженной () волн, взятых в одном и том же поляризационном базисе (). Пару этих выражений можно записать в матричной форме.
Таблицу комплексных величин
называют матрицей рассеяния. В данной записи матрица рассеяния образована поляризационными составляющими эффективной длины цели.
В дальнейшем будем рассматривать в качестве основной характеристики цели матрицу эффективной длины
Матрицу эффективной длины целесообразно представить в виде
где
Таким образом, чтобы получить матрицу эффективной длины цели для однокомпозиционной схемы измерения ( т.е. антенна является приемной к передающей достаточно найти значения модулей матрицы и размерностей их аргументов .Для этог0 осуществляют излечение и прием сигналов для двух составляющих выбранного поляризационного базиса раздельно.
При излучении электромагнитных воли вертикальной поляризации и при приеме вертикально и горизонтально поляризованных составляющих отраженного сигнала, можно измерить модули и разность фаз . При излучении величин с горизонтальной линейной поляризацией находят соответственно и . Основная трудность появляется при прямом измерении разности фаз . Для этого требуется излучать раздельно по времени либо по частоте два зондирующих колебания: с горизонтальной и вертикальной поляризацией.
ЛИТЕРАТУРА
1. Фок В. А. Дифракция на выпуклом теле. - ЖЭТФ, 1945, т. 15, № 12, с. 693 - 698
2. Васильев Е. Н. Возбуждение гладкого идеально проводящего тела вращения. - Изв. Вузов СССР. Сер. Радиофизика, 1959, т. 2, № 4, с. 588 - 601.
3. Андерсеан А. Д. Рассеяние на цилиндрах с произвольным поверхностным импедансом. - ТИИЭР, 1965, т. 53, № 8, с. 1007-1013.
4. Хенл Х., Мауэ А., Вестпфаль К. Теория дифракции. - М.: Мир, 1964. - 428 с.
5. Марков Г. Т., Чаплин А. Ф. Возбуждение электромагнитных волн. - М.: Радио и связь, 1983 - 296 с.
6. Арнольд В. И. Обыкновенные дифференциальные уравнения. - М.: Наука, 1984. - 271 с.
7. Тихонов А. Н., Самарский А. А. Уравнения математической физики. - М.: Наука, 1972. - 735 с.
8. Вычислительные методы в электродинамике / Под ред. Р. Миттры. - М.: Мир, 1977. - 485 с.
9. Панасюк В. В., Саврук М. П., Назарчук З. Т. Метод сингулярных интегральных уравнений в двухмерных задачах дифракции. - Киев: Наукова думка, 1984. - 343 с.
10. Михлин С. Г. Вариационные методы в математической физике. - М.: Наука, 1970, - 420 с.
11. Хижняк Н. А. Функция Грина уравнений Максвелла для неоднородных сред. - ЖТФ, 1958, т. 28,№ 7, с. 1592 - 1604.
12. Кравцов В. В. Интегральные уравнения в задачах дифракции. - В кн.: Вычислительные методы и программирование. - М.: Изд-во МГУ, 1966, вып. У, с. 260 - 293.
13. Васильев Е. Н., Гореликов А. И., Фалунин А. А. Тензорная функция Грина координатах вращения. - В кн.: Сб. научно-методических статей по прикладной электродинамике. - М.: Высшая школа, 1980, вып. 3, с. 3 - 24.
14. Белостоцкий В. В., Васильев Е. Н. Интегральное уравнение сферического открытого резонатора с диэлектрическим шаром. - В кн.: Вычислительные методы и программирование. - М.: Высшая школа, 1978, вып. 2, с. 101 - 111
15. Васильев Е. Н., Серегина А. Р., Седельникова З. В. Дифракция плоской волны на теле вращения, частично покрытом слоем диэлектрика. - Изв. Вузов СССР. Сер. Радиофизика, 1981, т. 24, № 6, с. 753 - 758
16. Хемминг Р. В. Численные методы. - М.: Наука, 1972. - 400 с.
17. Васильев Е. Н., Малов В. В., Солохудов В. В. Дифракция поверхностной волны на открытом конце круглого полубесконечного диэлектрического волновода. - Радиотехника и электроника, 1985, т. 30, № 5, с. 925 - 933.
18. Фокс А., Ли Т. Резонансные типы колебаний в интерферометре квантового генератора. - В кн.: Лазеры. - М.: ИЛ, 1963. - 155 с.
19. Каценеленбаум Б. 3., Сивов А. Н. Строгая постановка задачи о свободных и вынужденных колебаниях открытого резонатора. - Радиотехника и электроника, 1967, т. 12, 11, с. 1184- 1193.
20. Вайнштейн Л. А. Открытые резонаторы и открытые волноводы. - М.: Сов. радио, 1966. - 475 с.
21. Slерiаn В. Ргоbаtе spheroidal wave function, fourier analisis and uncertainly - 1У. Extension to many dimension, generalised prolate spheroidal functions. - Bell System Techn. J., 1964, v. 143, . 11, р. 1042- 1055.
ПРИЛОЖЕНИЯ
Приложение А
Теорема продолжимости для функций спектральной плотности
Это приложение относится к теореме продолжимости для функций спектральной плотности, обсуждавшихся в разделе Ш-Е. Подразумевается, что каждая окрестность каждой точки в К имеет строго положительную -меру. Это условие гарантирует, что корреляционные векторы, соответствующие импульсам в К, могут быть аппроксимированы посредством корреляционных векторов, соответствующим непрерывным, строго положительным функциям спектральной плотности.
Теорема продолжимости для спектральных функций плотности : Если каждая окрестность каждой точки в К имеет строго положительную меру , то
1/если равномерно ограничено от нуля по К, то
,
2/если , то
для некоторых непрерывных, строго положительных функций .
Доказательство : Первое утверждение может быть доказано посредством рассмотрения отображения ограниченной функции на вектор , определяемый путем
(А1)
То, что имеет равномерное ограничение от ноля означает, что для некоторого для всех . Поскольку Функции являются линейно-незазисимыми функциями на К и, так как каждая окрестность каждой точки в К содержит множество со строго положительной мерой, то отсюда следует, что отражением множества ограниченных -полиномов
(А2)
при /A1/, является окрестность О. Поэтому отражением
(А3)
является подмножество Е, которое находится в окрестности .
Следовательно, .
Второе утверждение может быть доказано посредством рассмотрения множества корреляционных векторов, соответствующих функциям спектральной плотности, которые являются интегрируемыми, непрерывными и строго положительными /следовательно, с ограничением от нуля/,
является выпуклым и, из доводов, приведенных выше, следует, что - открыто. Легко показать., что векторы для находятся в замыкании . Из теоремы Каратеодори [16] следует, что каждый может быть записан в виде положительной суммы 2М + I таких . Поскольку каждый находится в замыкании , то отсюда следует, что каждый находится там же. Поэтому замыканием является Е. Два открытых выпуклых множества с одинаковым замыканием должны быть идентичными. Поскольку Е находится в замыкании как , так и , то отсюда следует, что
Приложение В
Теорема представления
Теорема представления раздела IУ-А является простым распространением теоремы Каратеодори [16] для корреляционных векторов на границе Е с использованием теоремы о продолжимости. Это обобщение "теоремы С" Каратеодори [9, гл. 4] для многократных измерений. Ввиду вывода метода Писаренко в разделе 1У, как линейной программы, теорема представления может также рассматриваться, как вид фундаментальной теоремы линейного программирования. [l8].
Теорема представления: Если находится на границе Е, то для некоторых 2М неотрицательных и некоторых :
(В1)
Доказательство: Рассмотрим компактное выпуклое множество , которое является выпуклой оболочкой . По теореме Каратеодори,. любой элемент в Е может быть выражен в виде выпуклой комбинации 2М+1 элементов А
(B2)
при и . Если одно из равно нулю, доказательство завершено. Иначе, поскольку находится на границе , имеется некоторый ненулевой , такой что
(В3)
Итак, для каждого , должны быть линейно зависимыми, следовательно имеются некоторые , не все нули, так что . Пусть является числом с наименьшим значением, так что для некоторого .
Тогда
(B4)
Один из этих коэффициентов равен нулю, что делает равным это выражение сумме только 2М членов. Признание того, что любой элемент Е является масштабированной версией элемента , завершает доказательство.
Отметим, что для случая временной последовательности, может быть выражен в виде суммы не более, чем М комплексных экспоненциалов, в то время, как вышеприведенная теорема гарантирует только представление в терминах 2М экспоненциалов, Это не недостаток доказательства, а подлинная особенность проблемы, как показывает следующий одномерный пример.
Пример BI : . Предположим, что находится на прямой части границы и, как показа-
но на рис.7. Ясно, что имеет единственное представление в виде выпуклой суммы членов А в терминах двух корреляционных векторов, соответствующих и ,
Приложение С
Единственность оценки Писаренко
Как обсуждалось в разделе IУ-А, опенка Писаренко является единственной, если один и только один спектр может быть связан с каждым корреляционным вектором на границе Е. Тривиальные проблемы единственности появляются в результате, если два отдельных в приводят к одному и тому же . В -более общем смысле рассмотрим множество корреляционных векторов, соответствующих нулевому множеству некоторого ненулевого положительного полинома
(С1)
Любой вектор , который превращает в ноль внутреннее произведение с р ,может быть выражен в виде суммы положительных составляющих векторов из множества . Отсюда следует, что если это множество является линейно независимыми, то представление единственно. И наоборот, если это множество линейно зависимо, то можно построить на границе Е, который имеет более одного спектрального представления. Если множество линейно зависимо, то имеется конечная совокупность ненулевых вещественных чисел и , таких что
(С2)
Поскольку для всех , то должно быть, по крайней мере, одно - строго положительное и одно - строго отрицательное. Итак,
(С3)
является ненулевым вектором корреляции на границе Е с, по крайней мере, двумя спектральными представлениями.
Поэтому оценка Писаренко является единственной тогда и только тогда, когда множество корреляционных векторов, соответствующих нулю каждого ненулевого положительного полинома, линейно независимо. В частности, чтобы оценка Писаренко была единственной, никакой ненулевой положительный полином не может иметь более 2М нулей, это условие подобно, хотя и не так строго, условию Хаара [23], которое включает все полиномы, а не только положительные.
Факторизация полиномов в случае временной последовательности дает сильный результат. В случае временной последовательности ненулевой положительный полином может иметь не более М нулей. Кроме того, ненулевой положительный полином может быть построен так, что он равен нулю в М или менее произвольных точках и больше нигде. Это означает /Пример 4.I/ , что корреляционный вектор в имеет единственное спектральное представление и что этот спектр состоит из и или менее импульсов. Кроме того, это означает, что любой спектр, состоящий из М или менее импульсов, имеет корреляционный вектор в .
Однако, простой пример показывает,, что нет гарантии того, что оценка Писаренко будет единственной в большинстве многомерных ситуаций. Рассмотрим ненулевой положительный полином
(С4)
для некоторого ненулевого . Нулевое множество включает часть гиперплоскости
(С5)
которая находится в К. Многие спектральные основы, имеющие практический интерес, пересекают эту гиперплоскость в бесконечном числе точек, подразумевая существование некоторого корреляционного вектора на границе Е с неединственным спектральным представлением. Эта проблема неединственности аналогична неединственности в многомерной чебышевской аппроксимации [24].
ИЛЛЮСТРАЦИИ
Рис.1 ПИП из трех ИП
Рис.2 Спектральная основа для решетки ПИП : I - основа
Рис.3 Е и Р для и . /а/ Сечение Е и Р при и /b/ Сечение Е и Р при .
Рис. 4 Е и Р для и . /а/ Сечение Е и Р при и /b/ Сечение Е и Р при .
Рис.5 Аппроксимация спектральной основы посредством выборки ; сечение при
Рис.6 Разложение вектора на вектор на границе Е плюс кратное данного вектора .
Рис.7 Е для и . /а/ Сечение по Е при и /b/ Сечение по Е при .
Похожие работы
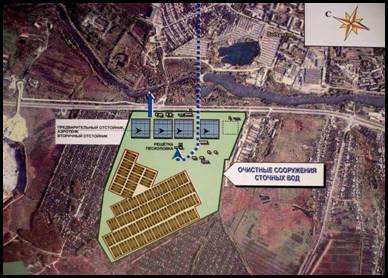
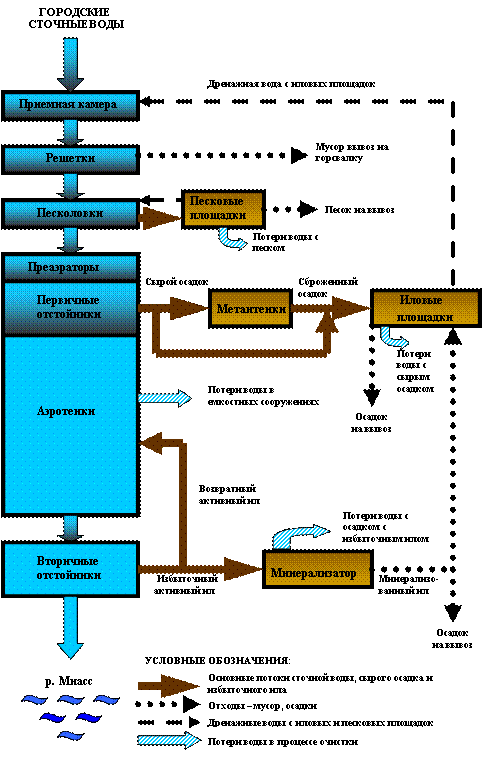
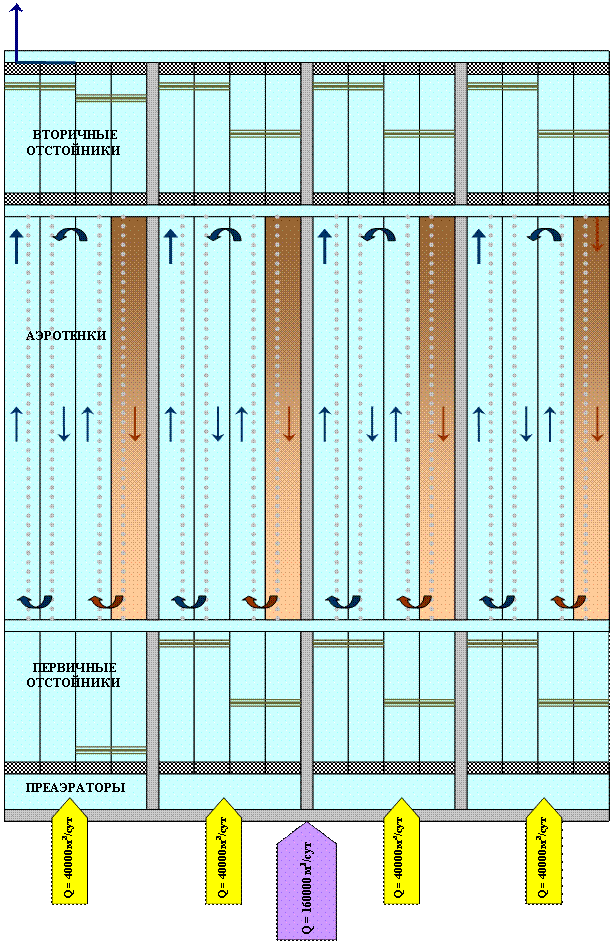
... быть использована в качестве присадочного материала при подготовке осадка к обезвоживанию. Это позволяет снизить расход химических реагентов. Проектирование новых и реконструкцию существующих комплексов для обработки осадков на очистных станциях и установках рекомендуется выполнять применительно к унифицированным производительностям очистных установок и станций, а также к местным условиям и ...
... педагогические условия и приемы, обеспечивающие их коррекцию путем переструктурирования мотивационной сферы личности и расширения у студентов взаимосвязей учебно-профессиональных и физкультурных мотивов. Существенной особенностью данного исследования было использование метода репертуарных решеток, что позволило изучать у студентов мотивы и их структуры, максимально приближенные к независимой от ...
... (в фазе трех-пяти листьев у сорняков). При использовании гербицидов количество механических операций можно сократить. Обработку гербицидами начинают за З-4 дня до появления всходов. В интенсивной технологии возделывания картофеля важное мecтo занимает окучивание. Задача окучивания – не только удаление сорняков, рыхление почвы вокруг растений и создание лучших условий для клубнеобразования, но ...
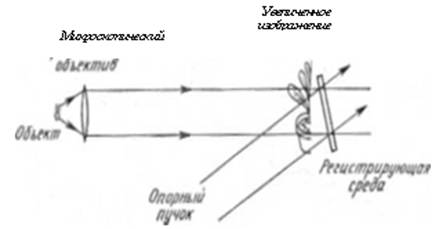
... перемещений лежит от долей микрона до нескольких миллиметров. Голографическая интерферометрия и спекл-интерферометрия являются двумя широкими областями, используемыми для обнаружения перемещений методами когерентной оптики. Кратко рассмотрим каждую из них, чтобы иметь возможность сравнивать их между собой. Голографическая интерферометрия основывается на достоинстве голографии (т. е. возможности ...


0 комментариев