Навигация
Оптимальные и адаптивные системы
![]() - корни
вещественные
- корни
вещественные
![]()
![]()
Сумма двух экспонент представляет собой:
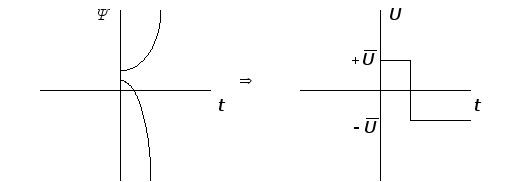
Если ![]() ,
то корни
комплексно-сопряженные
и решение будет
представлять
собой периодическую
функцию. В реальной
системе, переключений
не более 5 - 6.
,
то корни
комплексно-сопряженные
и решение будет
представлять
собой периодическую
функцию. В реальной
системе, переключений
не более 5 - 6.
Метод поверхности переключений
Данный метод позволяет найти управление функций переменной состояния для случая когда оптимальное управление носит релейный характер
![]() .
.
Таким образом этот метод можно применять при решении задач оптимального быстродействия, для объекта с аддитивным управлением
![]() ,
,
![]() .
.
Суть метода заключается в том, чтобы во всём пространстве состояний выделить точки, где происходит смена знака управления и объединить их в общую поверхность переключений.
![]() ,
,
![]() - поверхность
переключений
- поверхность
переключений
![]() .
.
Закон управления будет иметь следующий вид
![]() .
.
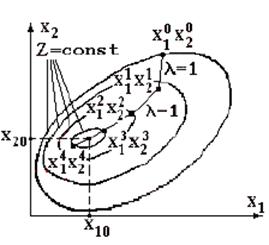
Для формирования поверхности переключений удобнее рассматривать переход из произвольной начальной точки в начало координат
![]() .
.
Если конечная точка не совпадает с началом координат, то необходимо выбрать новые переменные, для которых это условие будет справедливо.
Имеем объект вида
![]() .
.
Рассматриваем
переход ![]() ,
с критерием
оптимальности
,
с критерием
оптимальности
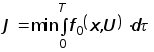 .
.
Этот критерий позволяет найти закон управления такого вида
![]() ,
,
с неизвестным ![]() ,
начальные
условия
,
начальные
условия ![]() нам также
неизвестны.
нам также
неизвестны.
Рассматриваем переход:
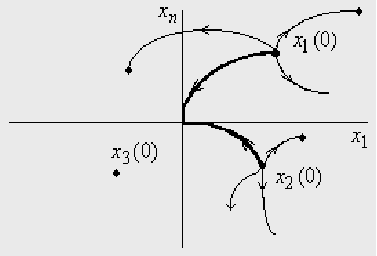
Метод обратного времени
(метод попятного движения)
Этот метод позволяет определить поверхности переключений.
Суть
метода заключается
в том, что начальная
и конечная
точки меняются
местами, при
этом вместо
двух совокупностей
начальных
условий остаётся
одна для ![]() .
.
Каждая из этих траекторий будет оптимальна. Сначала находим точки, где управление меняет знак и объединяем их в поверхность, а затем направление движения меняем на противоположное.
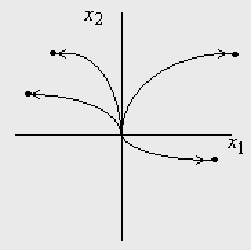
Пример
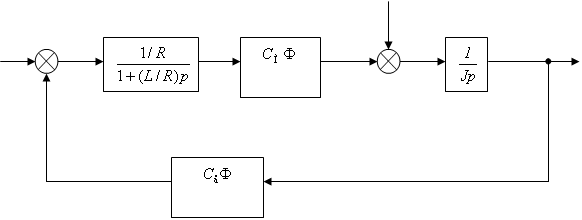
Передаточная функция объекта имеет вид
![]() .
.
Критерий оптимальности быстродействия
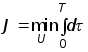
Ограничение
на управление ![]() .
.
Рассмотрим переход
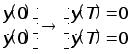 .
.
1)
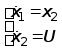 ,
,
2)
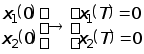 .
.
3)
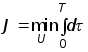
оптимальное управление будет иметь релейный характер
![]() .
.
4) Перейдём
в обратное
время (т.е. ![]() ).
В обратном
времени задача
будет иметь
такой вид
).
В обратном
времени задача
будет иметь
такой вид
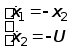 .
.
5) Рассмотрим два случая:
![]()
Получим уравнения замкнутой системы
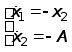 .
.
Воспользуемся
методом непосредственного
интегрирования,
получим зависимость ![]() от
от ![]() и поскольку
и поскольку ![]() -
-![]() ,
то имеем
,
то имеем
![]() ,
,
т.к.
начальные и
конечные точки
поменяли местами,
то ![]() ,
, ![]() получим
получим
![]() , (*)
, (*)
аналогично
![]()
![]()
подставив (*), получим
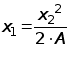 ,
,
отсюда
![]() .
.
Построим получившееся и по методу фазовой плоскости определим направление

![]()
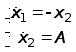
Применив метод непосредственного интегрирования, получим:
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() .
.
Функция будет иметь вид:
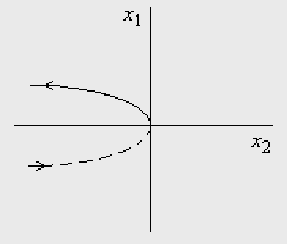
Изменив направление
точка смены знака
(точка переключения)
Общее аналитическое выражение:
![]() .
.
Уравнение поверхности:
![]() .
.
Оптимальный закон управления:
![]() ,
,
подставив уравнение поверхности, получим:
![]() .
.
Похожие работы
... luc – программа используется для разложения матрицы на треугольные сомножители; rluc – программа, которая отвечает за решение системы уравнений. 4. Разработка адаптивной системы управления режимами электропотребления 4.1 Функции автоматизированной системы Сбор, накопление и передача информации, характеризующей режим электропотребления комбината (информация о нагрузках). Сбор, накопление ...
... время решающее значение приобретает четкая аналитическая формулировка алгоритма решения задачи и реализация его с помощью ЭВМ.1.СИНТЕЗ СИСТЕМЫ УПРАВЛЕНИЯ КВАЗИСТАЦИОНАРНЫМ ОБЪЕКТОМ 1.1Построение информационной управляющей системы с элементами самонастройки. Для нестационарного динамического объекта управления, поведение которого описывается нестационарными дифференциальными уравнениями вида (1.1): ...
ости обработки. Для измерения этой температуры и управления процессом обработки наибольшее распространение нашел метод естественной термопары, образованной инструментом и деталью. Развиваемая естественной термопарой термо-ЭДС позволяет построить АСУ ТП, поддерживающую заданный температурный режим с точностью 2...3 %. Для успешного построения системы стабилизации температуры резания (СТР) ...
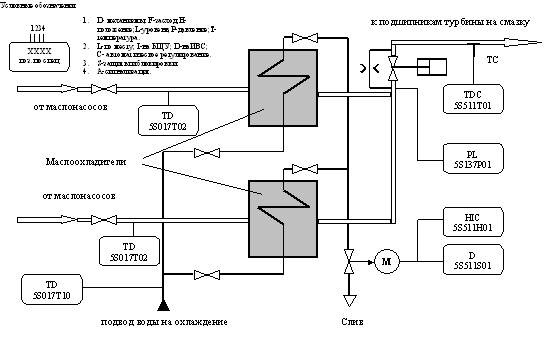
... : - по маслу 20кПа - по воде 20,1кПа Максимальное рабочее давление: - масла 0,5Мпа - воды 0,5МПа Функциональная схема системы регулирования температуры смазочного масла приведена на рис. 9. Она содержит два маслоохладителя параллельно ...
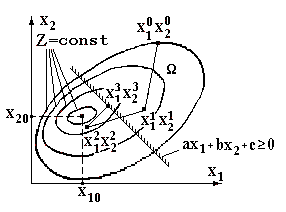

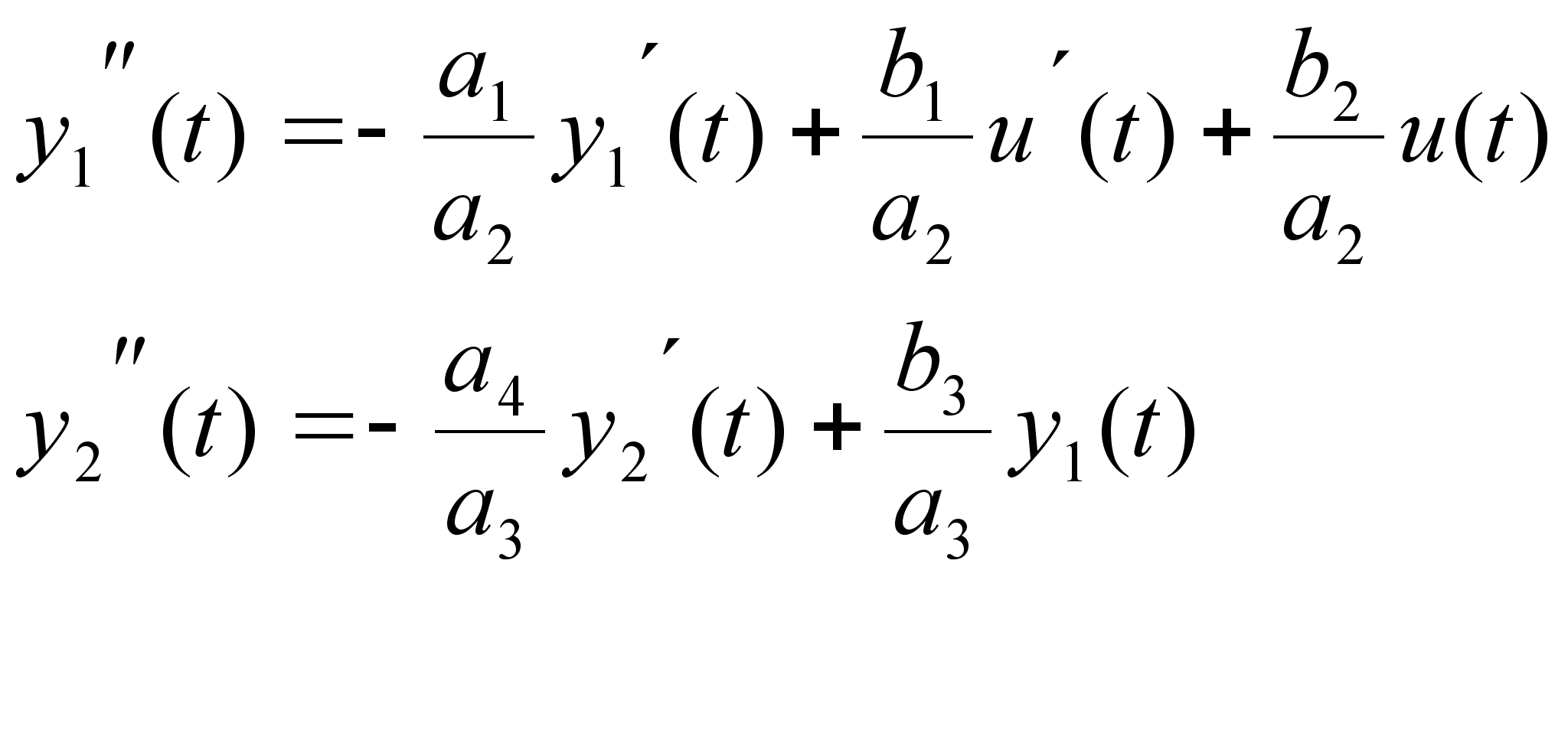


0 комментариев