Навигация
Экстремальные системы управления
12853
знака
0
таблиц
81
изображение
1. Экстремальные системы управления
Введение
Экстремальные СУ – это такие САУ, в которых один из показателей качества работы нужно удерживать на предельном уровне (min или max).
Классическим примером экстремальной СУ является система автоподстройки частоты радиоприёмника.
A
- экстремальная характеристика
w
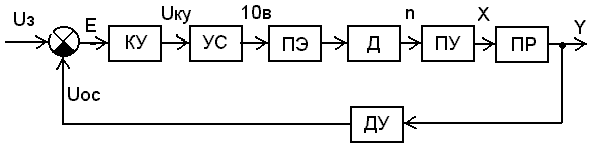
Рис.1.1. Амплитудно-частотная характеристика
1.1. Постановка задачи синтеза экстремальных систем
Объекты описываются уравнениями:
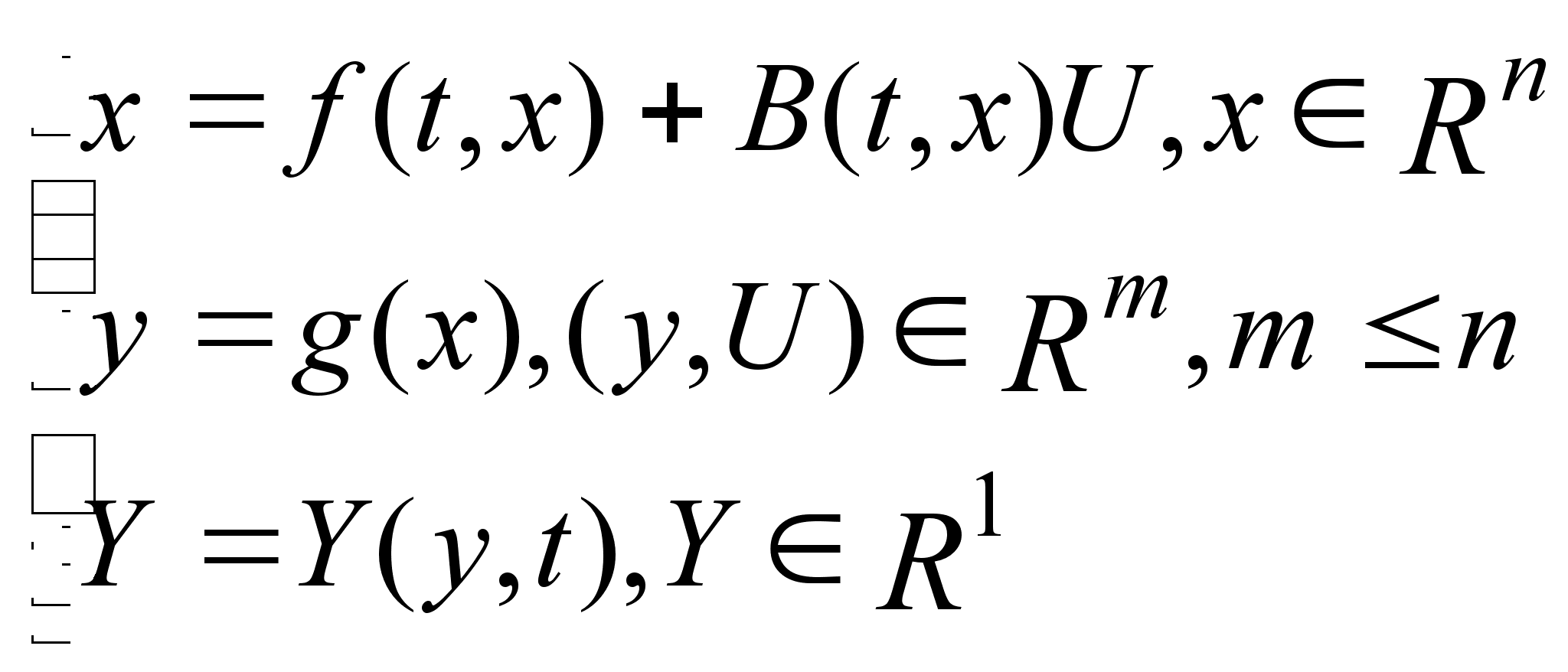(1.1)
Экстремальная характеристика дрейфует во времени.
Необходимо подобрать такое управляющее воздействие, которое позволяло бы автоматически находить экстремум и удерживать систему в этой точке.
U: extr Y=Yo (1.2)
Y
y – выход динамической части объекта
Y
– экстремальный
выход
Y
o -
точка
экстремума
yo y
Рис.1.2. Статическая экстремальная характеристика
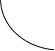
Необходимо определить такое управляющее воздействие, которое обеспечило выполнение свойства:
(1.3)
1.2. Условие экстремума
Необходимое условие экстремума – равенство нулю первых частных производных.
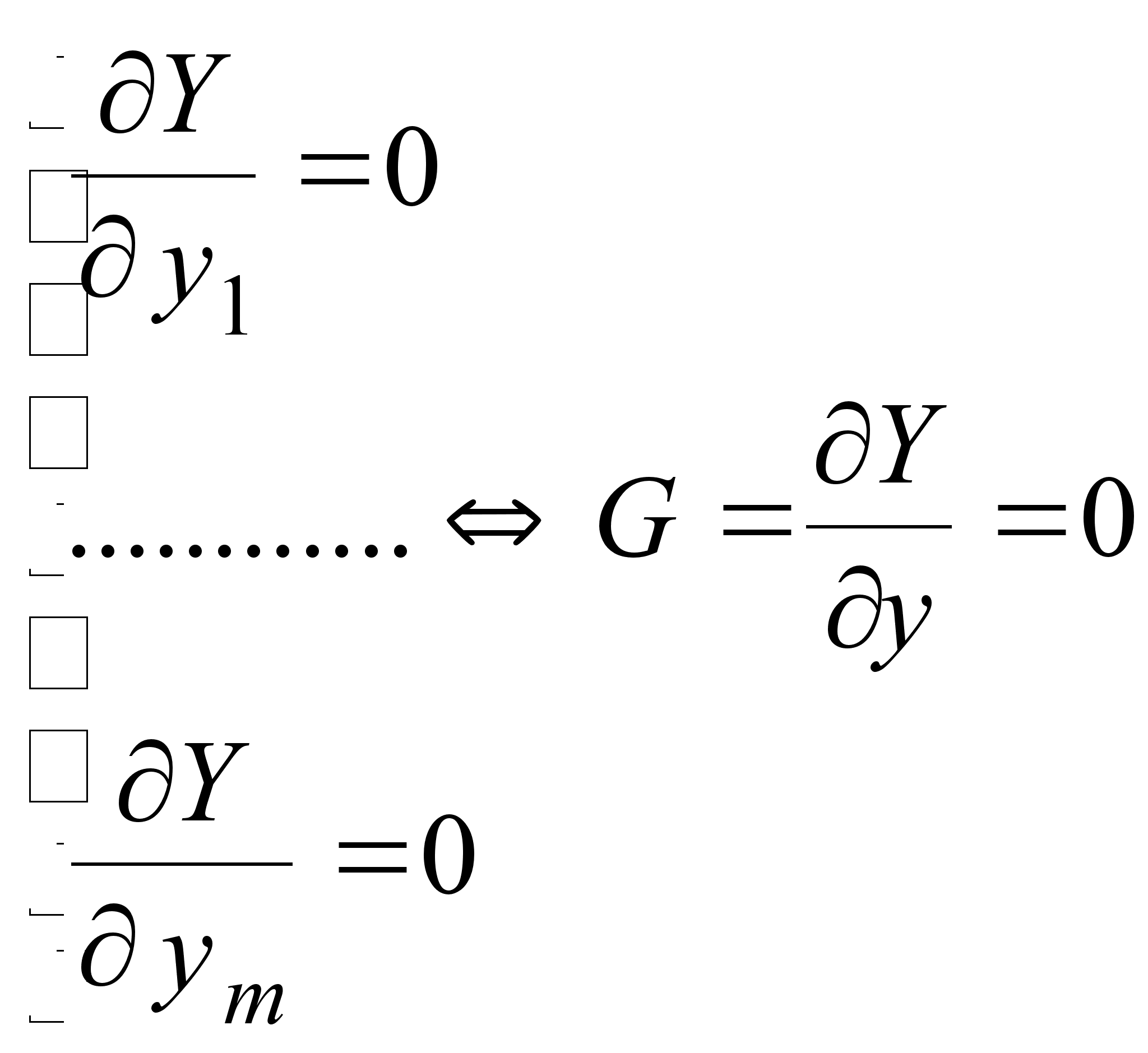G
– градиент. (1.4)
Достаточное условие экстремума – равенство нулю вторых частных производных .
При синтезе экстремальной системы необходимо оценить градиент, но вектор вторых частных производных оценить невозможно, и на практике, вместо достаточного условия экстремума используют соотношение:
-
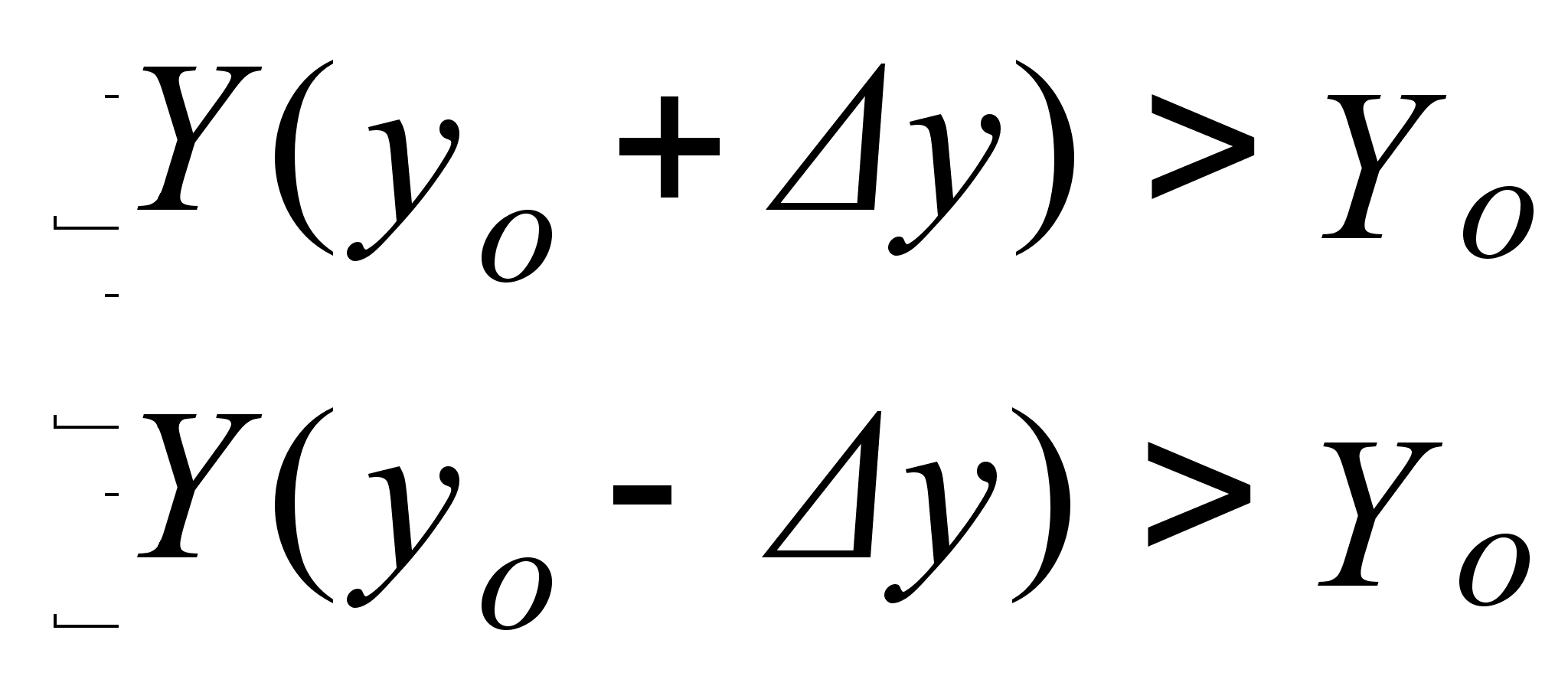min (1.5)
-
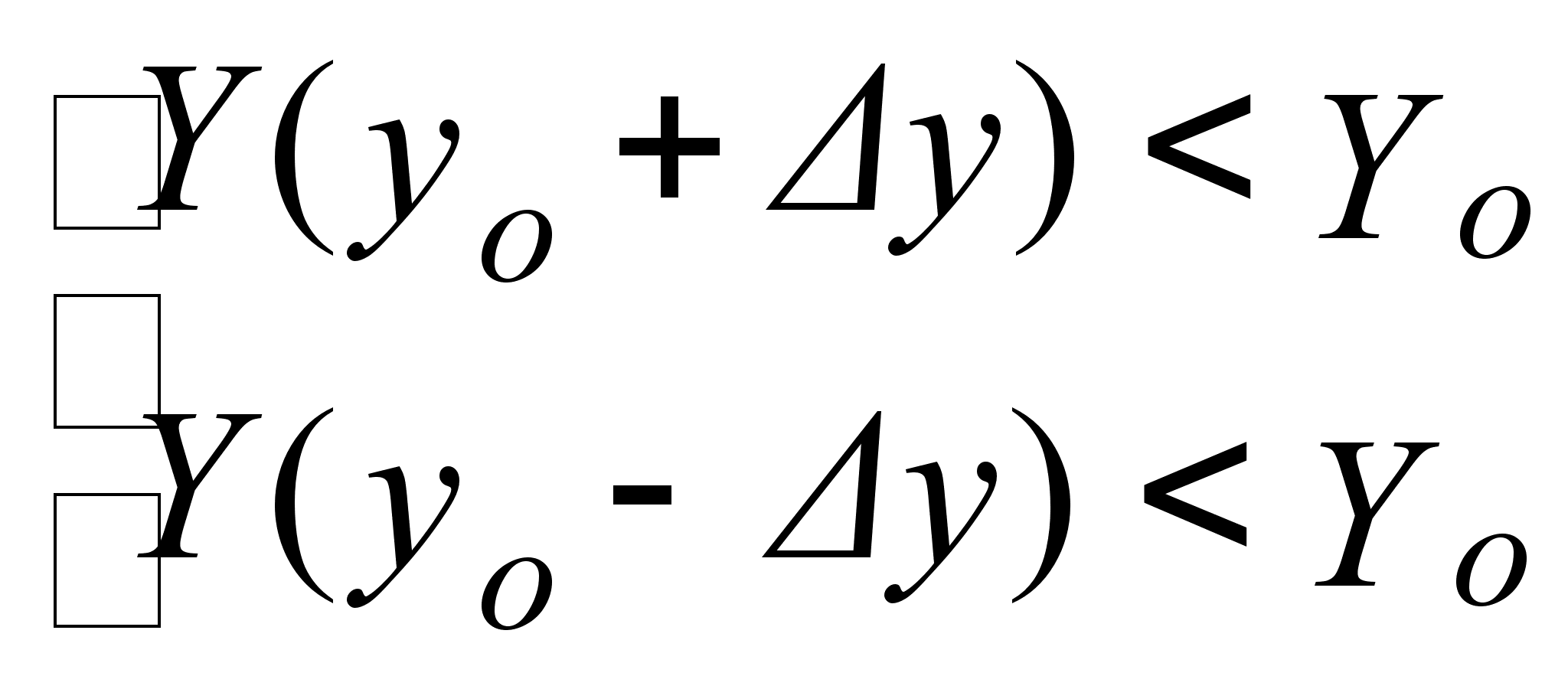max (1.6)
Этапы синтеза экстремальной системы:
оценка градиента.
Организация движения в соответствии с условием: G 0, т.е. движение к экстремуму.
Стабилизация системы в точке экстремума
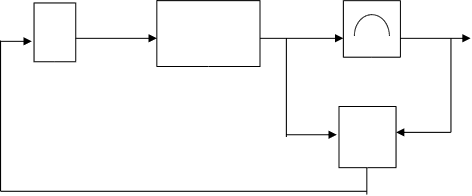
U 
=
f+BU y Y
экстремальная
регулятор характеристика
БОГ
Рис.1.3. Функциональная схема экстремальной системы
1.3. Виды экстремальных характеристик
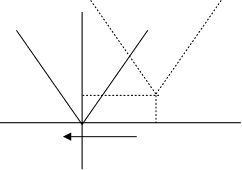
1) Унимодальная экстремальная характеристика типа модуля
Y
Y = k |y| (1.7)
Y = k1|y-y0(t)| + k2(t)
k1 – определяет наклон;
Yo yo – горизонтальный дрейф экстремума;
k2 – вертикальный дрейф экстремума.
y0
Рис. 1.4. Экстремальная характеристика типа модуля
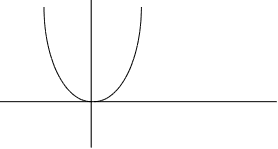
2) Экстремальная характеристика типа параболы
Y
Y = ky2; (1.8)
Y = k1 [y-yo(t)]2 + k2(t)
y
Рис. 1.5. Экстремальная характеристика типа параболы
3) В общем случае экстремальную характеристику можно описать параболой n-го порядка:
Y = k1|y-yo(t)|n + k2|y-yo(t)|n-1 + …+kn| y-yo(t)| + kn+1(t). (1.9)
4) Векторно-матричное представление
Y = yTBy (1.10)
1.4. Способы оценки градиента
1.4.1. Способ деления производных
Рассмотрим его на унимодальной характеристике, y- выход динамический части системы.
y
R1,
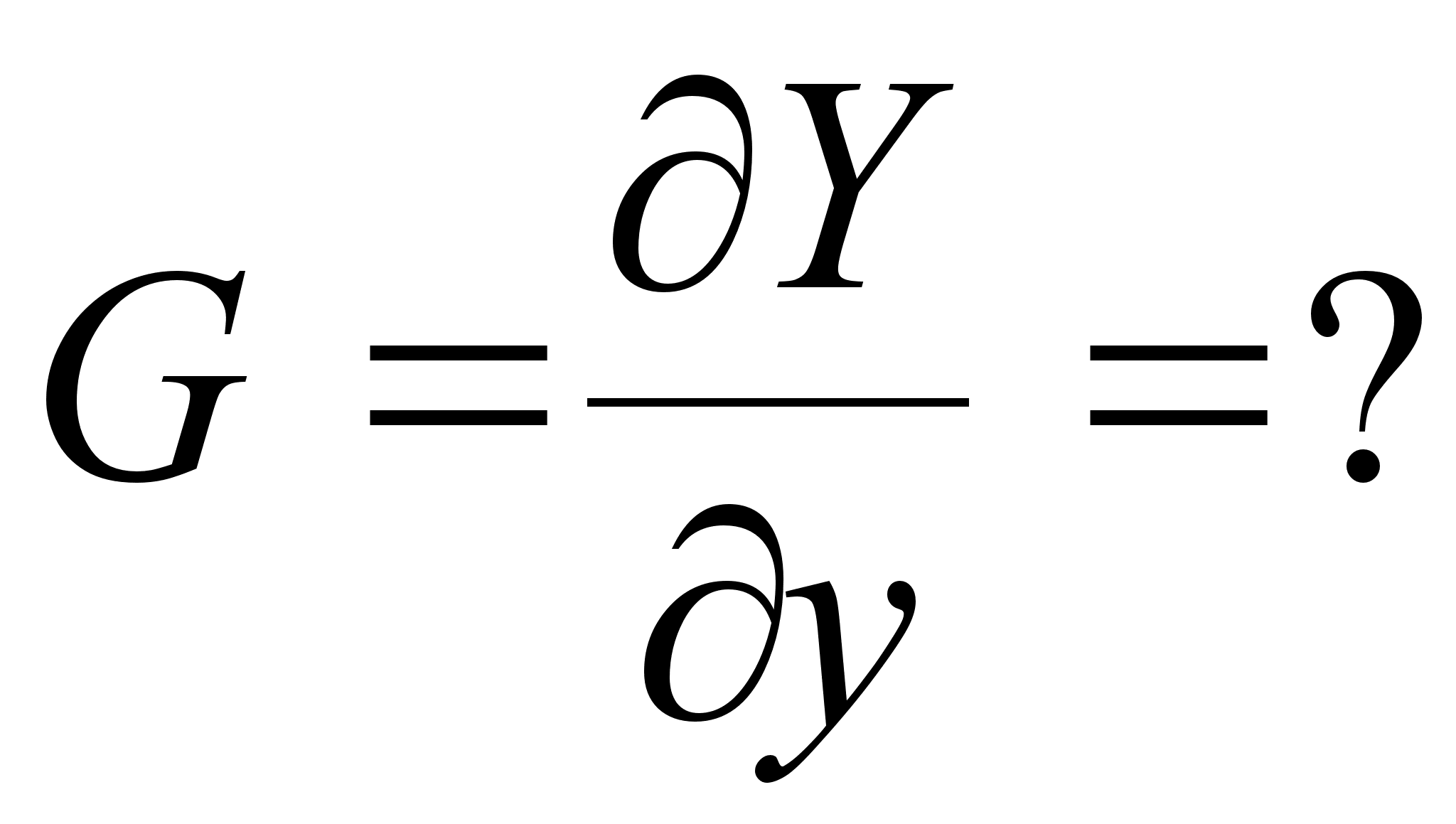Y
= Y(y,t)
Найдём полную производную по времени:
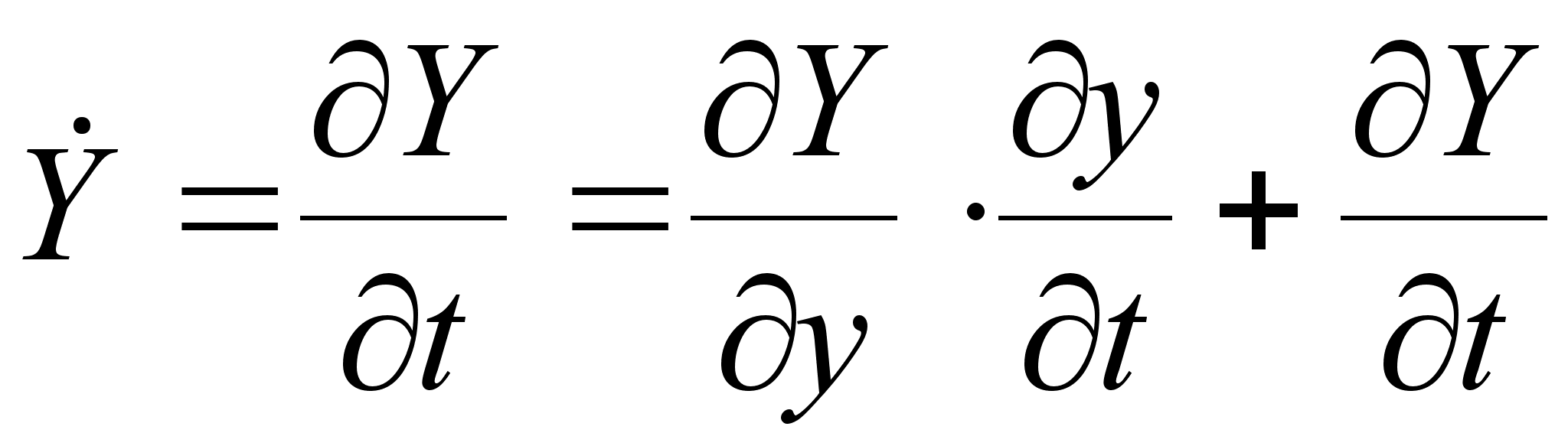(1.11)
При
медленном
дрейфе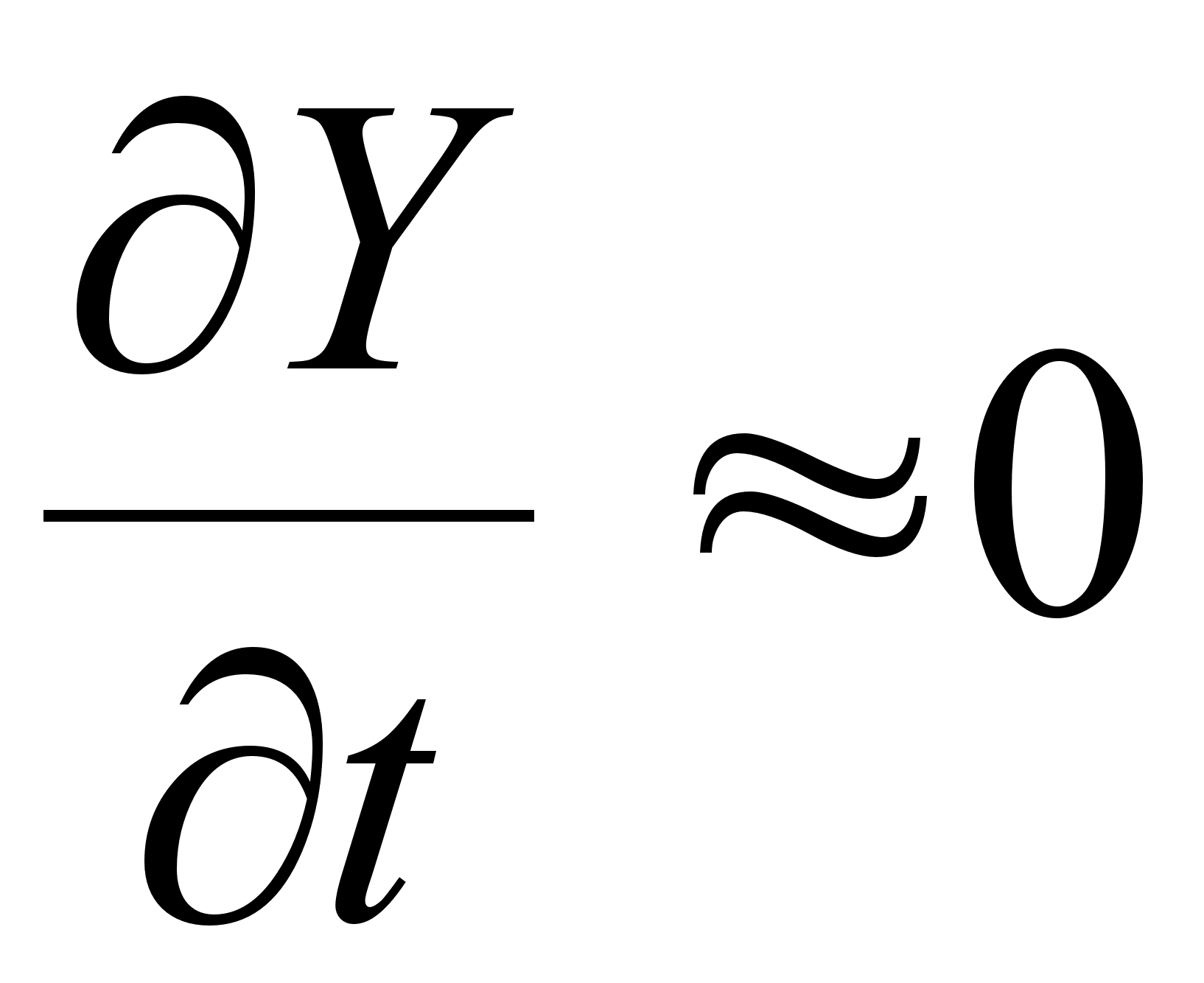 
,
таким образом
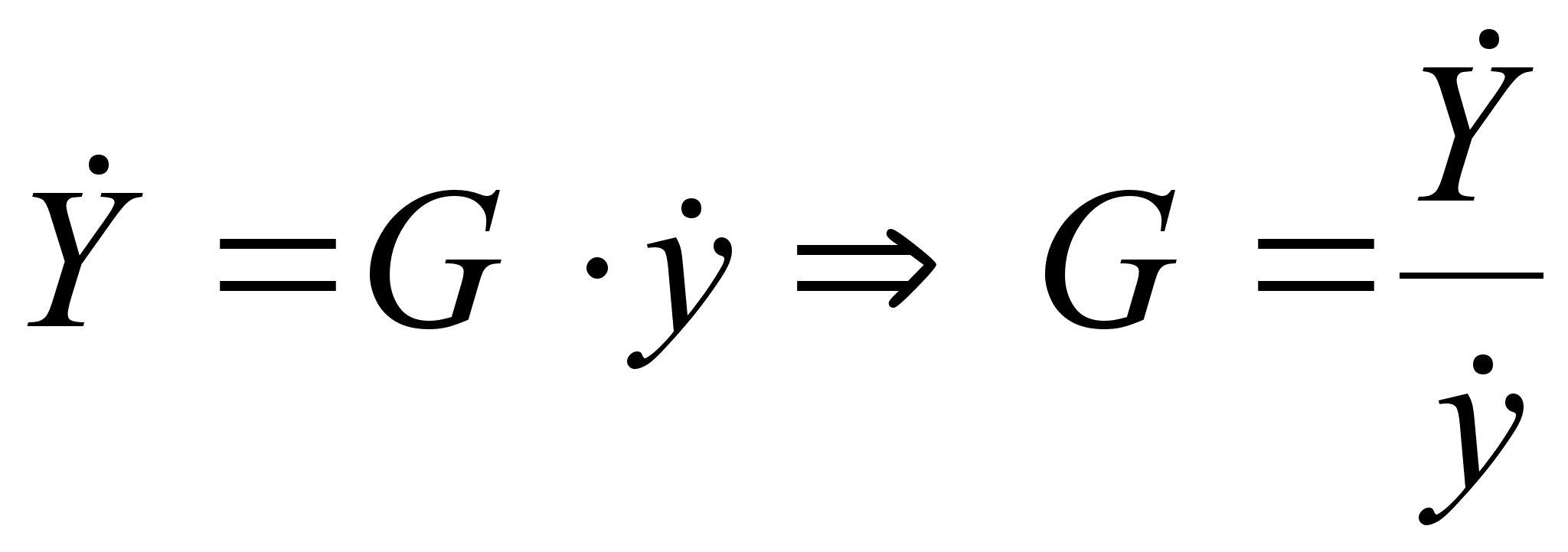(1.12)
Достоинство: простота.
Недостаток: при малых
Похожие работы
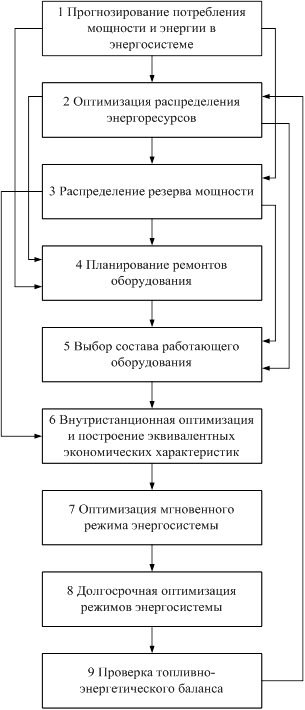
... luc – программа используется для разложения матрицы на треугольные сомножители; rluc – программа, которая отвечает за решение системы уравнений. 4. Разработка адаптивной системы управления режимами электропотребления 4.1 Функции автоматизированной системы Сбор, накопление и передача информации, характеризующей режим электропотребления комбината (информация о нагрузках). Сбор, накопление ...
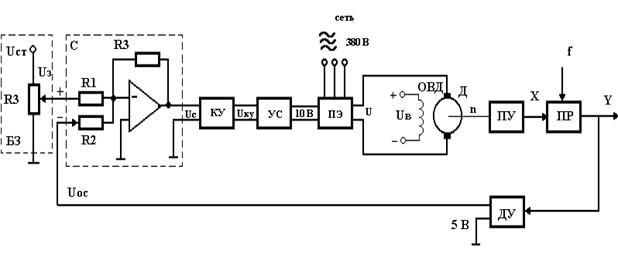
... время решающее значение приобретает четкая аналитическая формулировка алгоритма решения задачи и реализация его с помощью ЭВМ.1.СИНТЕЗ СИСТЕМЫ УПРАВЛЕНИЯ КВАЗИСТАЦИОНАРНЫМ ОБЪЕКТОМ 1.1Построение информационной управляющей системы с элементами самонастройки. Для нестационарного динамического объекта управления, поведение которого описывается нестационарными дифференциальными уравнениями вида (1.1): ...
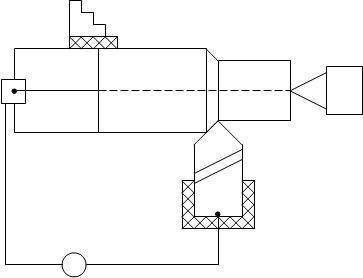
ости обработки. Для измерения этой температуры и управления процессом обработки наибольшее распространение нашел метод естественной термопары, образованной инструментом и деталью. Развиваемая естественной термопарой термо-ЭДС позволяет построить АСУ ТП, поддерживающую заданный температурный режим с точностью 2...3 %. Для успешного построения системы стабилизации температуры резания (СТР) ...
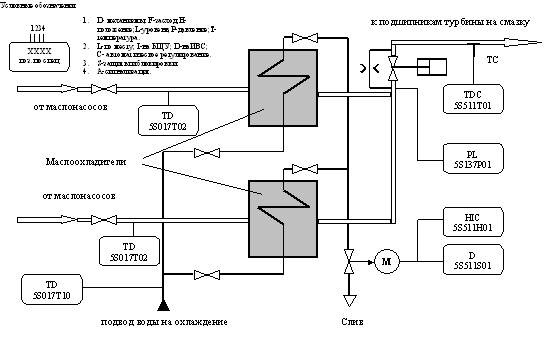
... : - по маслу 20кПа - по воде 20,1кПа Максимальное рабочее давление: - масла 0,5Мпа - воды 0,5МПа Функциональная схема системы регулирования температуры смазочного масла приведена на рис. 9. Она содержит два маслоохладителя параллельно ...
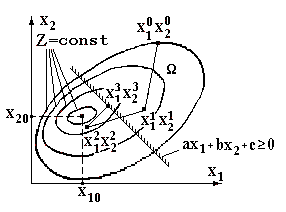
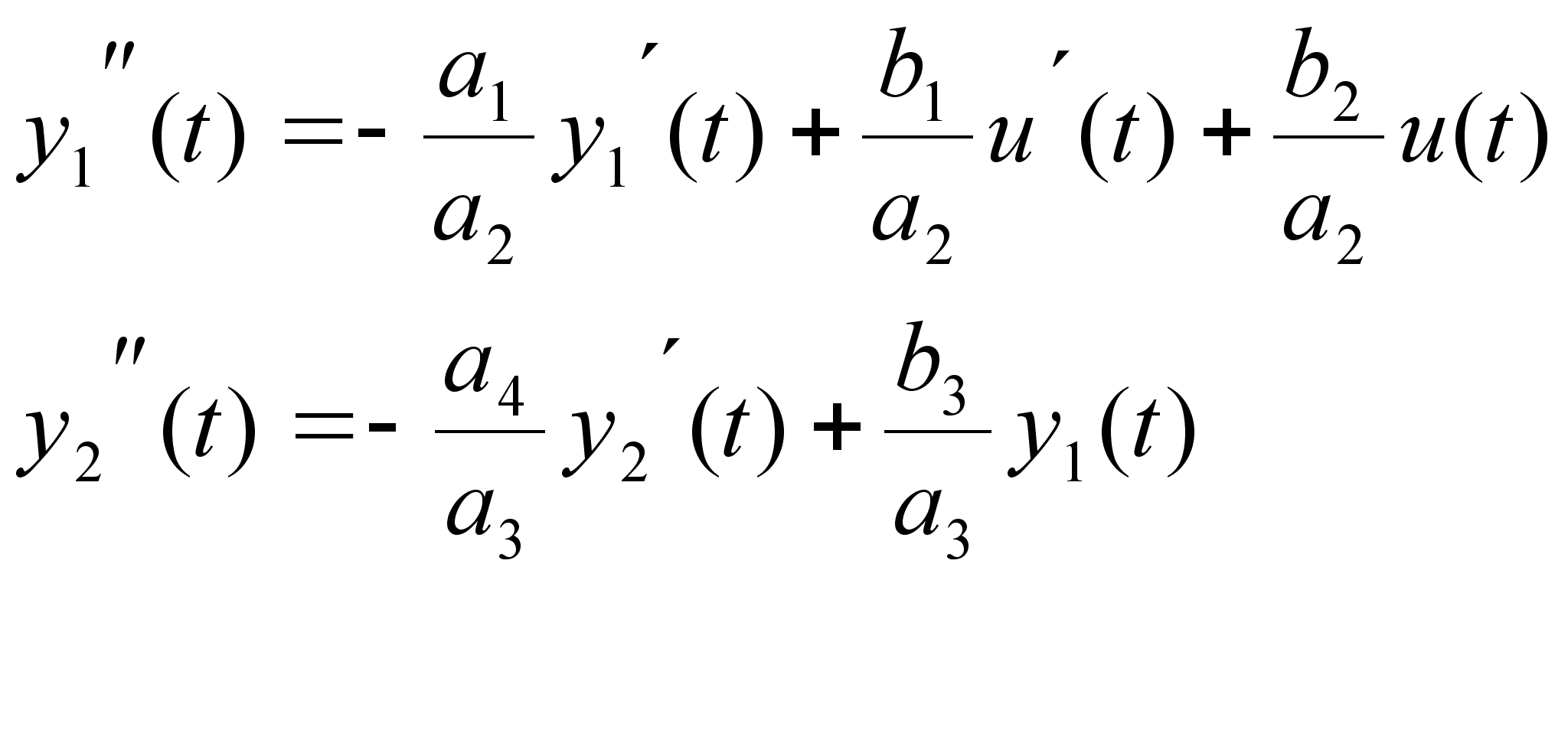
0 комментариев