Навигация
Прикладная теория цифровых автоматов
1. ПОБУДОВА ОБ'ЄДНАНОЇ ГСА
1.1. Побудова ГСА
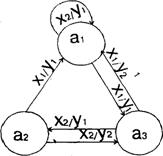
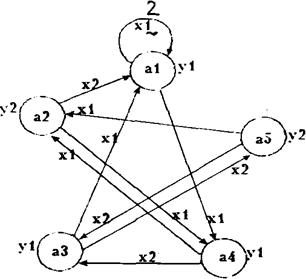
По описах граф-схем, приведених в завданні до курсової роботи, побудуємо ГСА Г1-Г5 (мал. 1.1-1.5), додавши початкові і кінцеві вершини і замінивши кожний оператор Yi операторною вершиною, а кожну умову Xi - умовною.
1.2. Методика об'єднання ГСА
У ГСА Г1-Г5 є однакові ділянки, тому побудова автоматів за ГСА Г1-Г5 приведе до невиправданих апаратурних витрат. Для досягнення оптимального результату скористаємося методикою С.І.Баранова, яка дозволяє мінімізувати число операторних і умовних вершин. Заздалегідь помітимо операторні вершини в початкових ГСА, керуючись слідуючими правилами:
1) однакові вершини Yi в різних ГСА відмічаємо однаковими мітками Aj;
2) однакові вершини Yi в межах однієї ГСА відмічаємо різними мітками Aj;
3) у всіх ГСА початкову вершину помітимо як А0, а кінцеву - як Ak.
На наступному етапі кожній ГСА поставимо у відповідність набір змінних PnО {P1...Pq}, де q=]log2N[, N -кількість ГСА. Означувальною для ГСА Гn ми будемо називати кон`юнкцию Pn=p1eЩ...Щpqn еО{0,1}, причому p0=щр, p1=р. Об'єднана ГСА повинна задовольняти слідуючим вимогам:
1) якщо МК Ai входить хоча б в одну часткову ГСА, то вона входить і в об'єднану ГСА Г0, причому тільки один раз;
2) при підстановці набору значень (е1...en), на якому Pq=1 ГСА Г0 перетворюється в ГСА, рівносильну частковій ГСА Гq.
При об'єднанні ГСА виконаємо слідуючі етапи:
-сформуємо часткові МСА М1 - М5, що відповідні ГСА Г1 - Г5;
- сформуємо об'єднану МСА М0;
- сформуємо системи дужкових формул переходу ГСА Г0;
- сформуємо об'єднану ГСА Г0.
1.3. Об'єднання часткових ГСА
Часткові МСА М1-М5 побудуємо по ГСА Г1-Г5 (мал.1.1) відповідно. Рядки МСА відмітимо всіма мітками Ai, що входять до ГСА, крім кінцевої Ak.
![]()
![]()
![]()
![]()
![]() ПОЧАТОК A0
ПОЧАТОК A0
![]()
![]()
![]()
 1
1
![]()
![]()
![]()
![]()
![]() 0 X1 1
0 X1 1
2
![]()
A1

![]() 3
3
![]()
![]() 0
0
![]()
![]()
![]()
![]()
![]() 4 X2 A2 1
4 X2 A2 1
 5
5
![]()
A3
![]()
6
![]()
A4
![]()
7
![]()
A5
![]()
![]()
![]()
![]() 8
8
![]()
A6
![]()
9
![]()
A7
![]()
10
![]()
![]() A8
A8
![]()
![]()
![]()
![]()
![]() КіНЕЦь Ak
КіНЕЦь Ak
![]()
Мал.1.1. Часткова граф-схема алгоритму Г1
![]()
![]()
![]()
![]()
![]() ПОЧАТОК A0
ПОЧАТОК A0
![]()
![]()
![]() 1
1

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() A1
A1
2
![]()
A7
![]()
 0 3 1
0 3 1
![]()
![]() X3
X3
4 5
![]()
![]() A9 A6
A9 A6
6 7
![]()
![]()
A10 A12
8 9
![]()
![]()
A3 A22
10
![]()
A11
![]()
![]()
![]()
![]()
![]() КіНЕЦЬ Ak
КіНЕЦЬ Ak
![]()
Мал.1.2. Часткова граф-схема алгоритму Г2
![]()
![]()
![]()
![]()
![]() ПОЧАТОК A0
ПОЧАТОК A0
![]()
![]()
1
![]()
A11
![]()
![]()
 0 2 1
0 2 1
![]()
![]()
![]()
![]()
![]()
![]() X1
X1
![]()
![]() 3 4
3 4
![]()
![]() A15 A16
A15 A16
![]()

![]() 6
6
5 1
![]()
![]()
![]()
![]() X3 A12
X3 A12
![]() 0
0
7 8
![]()
![]()
![]()
![]() A6 A13
A6 A13
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() КіНЕЦЬ Аk
КіНЕЦЬ Аk
![]()
Мал.1.3. Часткова граф-схема алгоритму Г3
![]()
![]()
![]()
![]()
![]() ПОЧАТОК A0
ПОЧАТОК A0
![]()
![]()

![]() 1
1
0 1
![]()
![]()
![]()
![]()
![]()
![]() X1
X1
2
![]()
A13
![]()
3
![]()
A9
![]()
![]()
![]()
![]() 4
4
![]()
A8
![]()
![]()
 5
5
1 X2
![]()
![]()
![]()
![]()
![]() 6 0
6 0
![]()
A17
![]()
7
![]()
A6
![]()
![]() 8
8
A2
![]()
9
![]()
A18
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() КіНЕЦЬ Ak
КіНЕЦЬ Ak
![]()
Мал.1.4. Часткова граф-схема алгоритму Г4
![]()
![]()
![]()
![]()
![]()
![]()
![]() ПОЧАТОК A0
ПОЧАТОК A0
1
![]()
A1
![]()
2
![]()
A6
![]()
3
![]()
A19
![]()
 4
4
0 1
![]()
![]()
![]()
![]() X1
X1
 5
5
0 X2
![]()
![]()
![]() 1
1
6
![]()
A20
![]()
7
![]()
A17
![]()
![]()
![]()
![]() 8
8
![]()
A2
![]()
![]()
![]()
![]()
![]() 9
9
A21
![]()
![]()
![]()
![]()
![]()
![]()
![]() КіНЕЦЬ Ak
КіНЕЦЬ Ak
![]()
Мал.1.5. Часткова граф-схема алгортиму Г5
Стовпці МСА відмітимо всіма мітками Ai, що входять до ГСА, крім початкової A0. На перетині рядка Ai і стовпця Aj запишемо формулу переходу fij від оператора Ai до оператора Aj. Ця функція дорівнює 1 для безумовного переходу або кон`юнкції логічних умов, відповідних виходам умовних вершин, через які проходить шлях з вершини з міткою Ai у вершину з міткою Aj.
За методикою об'єднання закодуємо МСА таким чином:
Таблиця 1.1
Кодування МСА
| МСА | P1P2P3 |
| М1 | 0 0 0 (щp1щp2щp3) |
| М2 | 0 0 1 (щp1щp2p3) |
| М3 | 0 1 0 (щp1p2щp3) |
| М4 | 0 1 1 (щp1p2p3) |
| М5 | 1 0 0 (p1щp2щp3) |
Часткові МСА М1-М5 наведені в табл.1.2-1.6
Таблиця 1.2
Часткова МСА М1
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | Ak | |
| A0 | щx1 | щx1щx2 | x1x2 | ||||||
| A1 | 1 | ||||||||
| A2 | 1 | ||||||||
| A3 | 1 | ||||||||
| A4 | 1 | ||||||||
| A5 | 1 | ||||||||
| A6 | 1 | ||||||||
| A7 | 1 | ||||||||
| A8 | 1 |
Таблиця 1.3
Часткова МСА М2
| A1 | A3 | A6 | A7 | A9 | A10 | A11 | A12 | A22 | Ak | |
| A0 | 1 | |||||||||
| A1 | 1 | |||||||||
| A3 | 1 | |||||||||
| A6 | 1 | |||||||||
| A7 | x3 | щx3 | ||||||||
| A9 | 1 | |||||||||
| A10 | 1 | |||||||||
| A11 | 1 | |||||||||
| A12 | 1 | |||||||||
| A22 | 1 |
Таблиця 1.4
Часткова МСА М3
| A6 | A12 | A13 | A14 | A15 | A16 | Ak | |
| A0 | 1 | ||||||
| A6 | 1 | ||||||
| A12 | 1 | ||||||
| A13 | 1 | ||||||
| A14 | щx1 | x1 | |||||
| A15 | x3 | щx3 | |||||
| A16 | 1 |
Таблиця 1.5
Часткова МСА М4
| A2 | A6 | A8 | A9 | A13 | A17 | A18 | Ak | |
| A0 | щx1 | x1 | ||||||
| A2 | 1 | |||||||
| A6 | 1 | |||||||
| A8 | x2 | щx2 | ||||||
| A9 | 1 | |||||||
| A13 | 1 | |||||||
| A17 | 1 | |||||||
| A18 | 1 |
Таблиця 1.6
Часткова МСА М5
| A1 | A2 | A6 | A17 | A19 | A20 | A21 | Ak | |
| A0 | 1 | |||||||
| A1 | 1 | |||||||
| A2 | 1 | |||||||
| A6 | 1 | |||||||
| A17 | 1 | |||||||
| A19 | x1щx2 | x1x2 | щx1 | |||||
| A20 | 1 | |||||||
| A21 | 1 |
На наступному етапі побудуємо об'єднану МСА М0, в якій рядки відмічені всіма мітками Аi, крім Аk, а стовпці - всіма, крім А0. На перетині рядка Аi і стовпця Аj запишемо формулу переходу, яка формується таким чином: Fij=P1fij1+...+Pnfijn (n=1...N). Де fijn-формула переходу з вершини Аi у вершину Аj для n-ої ГСА. Наприклад, формула переходу А0®А1 буде мати вигляд F0,1=щx1щp1щp2щp3+ щp1щp2p3+ +p1щp2щp3. У результаті ми отримаємо об'єднану МСА М0 (табл.1.7). Ми маємо можливість мінімізувати формули переходу таким чином: розглядаючи ГСА Г0 як ГСА Гn, ми підставляємо певний набір Pn=1, при цьому змінні p1..pq не змінюють своїх значень під час проходу по ГСА. Таким чином, якщо у вершину Аi перехід завжди здійснюється при незмінному значенні pq, то це значення pq в рядку Аi замінимо на “1", а його інверсію на “0". Наприклад, у вершину А3 перехід здійснюється при незмінному значенні щp1 і щp2, отже в рядку А3 щp1 і щp2 замінимо на “1", а p1 і p2 на “0". У результаті отримаємо формули F3,4=щp3, F3,11=p3. Керуючись вищенаведеним методом, отримаємо мінімізовану МСА М0 (табл.1.8).
По таблиці складемо формули переходу для об'єднаної ГСА Г0. Формулою переходу будемо називати слідуюче вираження: Ai®Fi,1А1+..+Fi,kАk, де Fi,j-відповідна формула переходу з мінімізованої МСА. У нашому випадку отримаємо слідуючу систему формул:
A0®щx1щp1щp2щp3A1+щp1щp2p3A1+p1щp2щp3A1+x1щx2щp1щp2щp3A2+x1x2щp1щp2щp3A3+
+щx1щp1p2p3A8+x1щp1p2p3A13+щp1p2щp3A14
A1®щp1щp3A2+p1щp3A6+щp1p3A7
A2®щp1щp2щp3A6+щp1p2p3A18+p1щp2p3A21
A3®щp3A4+p3A11
A4®A5
A5®А6
Таблиця 1.7
Об`єднана МСА Мo
A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | A17 | A18 | A19 | A20 | A21 | A22 | Ak | |
A0 | _ _ _ _ x1p1p2p3+ _ _ +p1p2p3+ _ _ +p1p2p3 | _ _ _ _ x1x2p1p2p3 | _ _ _ x1x2p1p2p3 | _ _ x1p1p2p3 | _ x1p1p2p3 | _ _ p1p2p3 | |||||||||||||||||
A1 | _ _ _ p1p2p3 | _ _ p1p2p3 | _ _ p1p2p3 | ||||||||||||||||||||
A2 | _ _ _ p1p2p3 | _ p1p2p3 | _ _ p1p2p3 | ||||||||||||||||||||
A3 | _ _ _ p1p2p3 | _ _ p1p2p3 | |||||||||||||||||||||
A4 | _ _ _ p1p2p3 | ||||||||||||||||||||||
A5 | _ _ _ p1p2p3 | ||||||||||||||||||||||
A6 | _ p1p2p3 | _ _ _ p1p2p3 | _ _ p1p2p3 | _ _ p1p2p3 | _ _ p1p2p3 | ||||||||||||||||||
A7 | _ _ x3p1p2p3 | _ _ _ p1p2p3 | _ _ _ x3p1p2p3 | ||||||||||||||||||||
A8 | _ x2p1p2p3 | _ _ _ p1p2p3+ _ _ +x2p1p2p3 | |||||||||||||||||||||
A9 | _ p1p2p3 | _ _ p1p2p3 | |||||||||||||||||||||
A10 | _ _ p1p2p3 | ||||||||||||||||||||||
A11 | _ _ p1p2p3 | ||||||||||||||||||||||
A12 | _ _ p1p2p3 | _ _ p1p2p3 | |||||||||||||||||||||
A13 | _ p1p2p3 | _ _ p1p2p3 | |||||||||||||||||||||
A14 | _ _ _ x1p1p2p3 | _ _ x1p1p2p3 | |||||||||||||||||||||
A15 | _ _ x3p1p2p3 | _ _ _ x3p1p2p3 | |||||||||||||||||||||
A16 | _ _ p1p2p3 | ||||||||||||||||||||||
A17 | _ _ p1p2p3 | _ p1p2p3 | |||||||||||||||||||||
A18 | _ p1p2p3 | ||||||||||||||||||||||
A19 | _ _ _ x1x2p1p2p3 | _ _ x1x2p1p2p3 | _ _ _ x1p1p2p3 | ||||||||||||||||||||
A20 | _ _ p1p2p3 | ||||||||||||||||||||||
A21 | _ _ p1p2p3 | ||||||||||||||||||||||
A22 | _ _ p1p2p3 |
Таблиця 1.8
Об`єднана мінімізована МСА Мo
A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | A17 | A18 | A19 | A20 | A21 | A22 | Ak | |
A0 | _ _ _ _ x1p1p2p3+ _ _ +p1p2p3+ _ _ +p1p2p3 | _ _ _ _ x1x2p1p2p3 | _ _ _ x1x2p1p2p3 | _ _ x1p1p2p3 | _ x1p1p2p3 | _ _ p1p2p3 | |||||||||||||||||
A1 | _ _ p1p3 | _ p1p3 | _ p1p3 | ||||||||||||||||||||
A2 | _ _ _ p1p2p3 | _ p1p2p3 | _ _ p1p2p3 | ||||||||||||||||||||
A3 | _ p3 | p3 | |||||||||||||||||||||
A4 | 1 | ||||||||||||||||||||||
A5 | 1 | ||||||||||||||||||||||
A6 | _ p1p2p3 | _ _ _ p1p2p3 | _ _ p1p2p3 | _ _ p1p2p3 | _ _ p1p2p3 | ||||||||||||||||||
A7 | x3p3 | _ p3 | _ x3p3 | ||||||||||||||||||||
A8 | x2p2p3 | _ _ p2p3+ _ +x2p2p3 | |||||||||||||||||||||
A9 | p2 | _ p2 | |||||||||||||||||||||
A10 | 1 | ||||||||||||||||||||||
A11 | 1 | ||||||||||||||||||||||
A12 | _ p2p3 | _ p2p3 | |||||||||||||||||||||
A13 | p3 | _ p3 | |||||||||||||||||||||
A14 | _ x1 | x1 | |||||||||||||||||||||
A15 | x3 | _ x3 | |||||||||||||||||||||
A16 | 1 | ||||||||||||||||||||||
A17 | _ _ p1p2p3 | _ p1p2p3 | |||||||||||||||||||||
A18 | 1 | ||||||||||||||||||||||
A19 | _ x1x2 | x1x2 | _ x1 | ||||||||||||||||||||
A20 | 1 | ||||||||||||||||||||||
A21 | 1 | ||||||||||||||||||||||
A22 | 1 |
A6®щp1p2p3A2+щp1щp2щp3A7+щp1щp2p3A12+p1щp2щp3A19+щp1p2щp3Ak
A7®x3p3A6+щp3A8+щx3p3A9
A8®x2p2p3A17+щp2щp3Ak+щx2p2p3Ak
A9®p2A8+щp2A10
A10®A3
A11®Ak
A12®щp2p3A22+p2щp3A13
A13®p3A9+щp3Ak
A14®щx1A15+x1A16
A15®x3A6+щx3Ak
A16®A12
A17®p1щp2щp3A2+щp1p2p3A6
A18®Ak
A19®x1щx2A2+x1x2A20+щx1A21
A20®A17
A21®Ak
A22®Ak
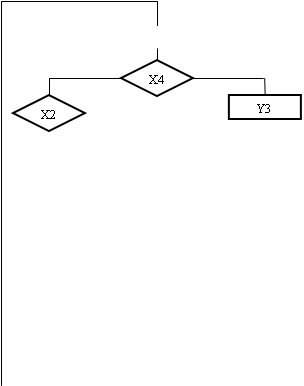
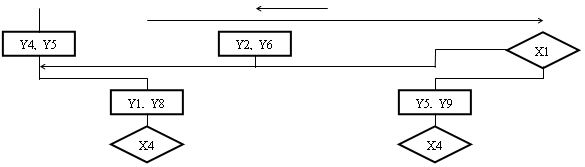
При побудові системи дужкових формул переходу необхідно кожну формулу привести до вигляду Аx1+Вщx1, де А і В -деякі вирази, а x1 і щx1-логічні умови переходу. Формули переходу для вершин А3, А4, А5, А9, А10, А11, А13, А14, А15, А16, А18, А20, А21, А22 вже є елементарними (розкладеними), а в інших є вирази виду Аn®xj(А) +щxjpi(В). Тут pi відповідає чекаючій вершині (мал.1.6). Подібних вершин в об'єднаній ГСА бути не повинно. Для їх усунення скористаємося слідуючим правилом: додавання виразу [PqАn] не змінить формулу, якщо набір Pq не використовується для кодування ГСА або вершина Аn відсутня в ГСА з кодом Pq. Таким чином, додаючи допоміжні набори, ми отримаємо можливість за допомогою елементарних перетворень звести формули до необхідного вигляду. Наприклад, формула A8®x2p2p3A17+щp2щp3Ak+щx2p2p3A спрощується таким чином A8=p3(x2p2A17+щx2p2Ak)+щp3щp2Ak=p3p2(x2A17+щx2Ak)+щp3щp2Ak=


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1 Xj 0
Pi 0
1
Мал.1.6 Приклад чекаючої вершини Pi
=[щp3p2(x2A17+щx2Ak)]+p3p2(x2A17+щx2Ak)+щp3щp2Ak+[p3щp2Ak]=щp2Ak+p2(x2A17+щx2Ak). Тут вершина А8 не зустрічається у ГСА ,в кодах яких присутні комбінації щp3p2 іp3щp2. Нижче наведено розклад усіх неелементарних формул переходу.
A0=p1(щp2щp3A1)+щp1(щx1щp2щp3A1+щp2p3A1+x1щx2щp2щp3A2+x1x2щp2щp3A3+
+щx1p2p3A8+x1p2p3A13+p2щp3A14)=p1(щp2щp3A1)+[p1щp2щp3A1]+
+щp1(p2(щx1p3A8+x1p3A13+щp3A14)+щp2(щx1щp3A1+p3A1+x1щx2щp3A2+
+x1x2щp3A3))=p1(щp2A1)+[p1p2A1]+щp1(p2(p3(щx1A8+x1A13)+щp3A14)+
+щp2(щp3(щx1A1+x1x2A3+x1щx2A2)+p3A1))= p1A1+щp1(p2(p3( щx1A8+
+x1A13)+щp3A14)+щp2(щp3(щx1A1+x1(x2A3+щx2A2))+p3A1))
A1=щp1(p3A7+щp3A2)+p1щp3A6+[p1p3A6]= щp1(p3A7+щp3A2)+p1A6
A2=p1(щp2p3A21)+щp1(щp2щp3A6+p2p3A18)= p1(щp2p3A21)+[p1щp2p3A21]+
+щp1(щp2щp3A6+[p2щp3A6]+p2p3A18+[p3щp2A18])=p1(щp2A21)+щp1(щp3A6+
+p3A18)=p1(щp2A21)+[p1p2A21]+щp1(щp3A6+p3A18)=p1A21+щp1(щp3A6+
+p3A18)
A6=p1(щp2щp3A19)+[p1щp2p3A19]+щp1(p2p3A2+щp2щp3A7+щp2p3A12+p2щp3Ak)=
=p1щp2A19+[p1p2A19]+щp1(p2(p3A2+щp3Ak)+щp2(щp3A7+p3A12))=p1A19+
+щp1(p2(p3A2+щp3Ak)+щp2(щp3A7+p3A12))
A7=p3(x3A6+щx3A9)+щp3A8
A8=p3(x2p2A17+щx2p2Ak)+щp3щp2Ak=p3p2(x2A17+щx2Ak)+щp3щp2Ak=
=[щp3p2(x2A17+щx2Ak)]+p3p2(x2A17+щx2Ak)+щp3щp2Ak+[p3щp2Ak]=щp2Ak+
+p2(x2A17+щx2Ak)
A12=щp2p3A22+p2щp3A13+[p2p3A22]+[щp2щp3A13]=p3A22+щp3A13
A17=p1щp2щp3A2+[p1щp2p3A2]+щp1p2p3A6+[щp1щp2p3A6]=p1щp2A2+[p1p2A2]+
+щp1p3A6+[щp1щp3A6]=p1A2+щp1A6
A19=x1(щx2A2+x2A20)+щx1A21
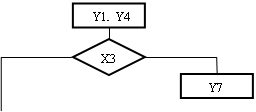
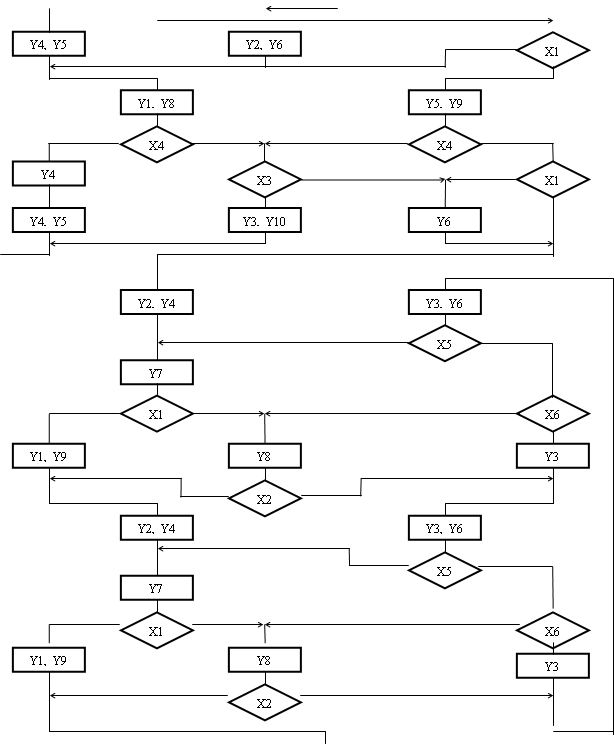
Об'єднану ГСА Г0 (мал.1.7) побудуємо відповідно до формул переходу, замінюючи кожну мітку Аi відповідною операторною вершиною Yt, а кожний вираз Xi і Pj відповідними умовними вершинами.
30
2.СИНТЕЗ АВТОМАТА З ПРИМУСОВОЮ АДРЕСАЦІЄЮ МІКРОКОМАНД.
Похожие работы
... булевої алгебри. Аналітичний спосіб задання булевих функцій займає особливе місце в проектуванні цифрових машин. Фактично, всі перетворення над булевими ф-ціями, необхідні для побудови цифрових машин, ведуться на аналітичному рівні. Розглянемо області визначення булевоі ф-ції. Як уже відмічалось, між двійковими наборами і двійковими числами існує взаємнооднозначна відповідність. Отже, існує 2n рі ...
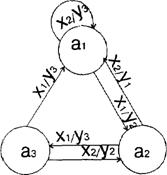
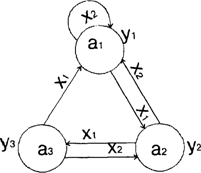
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... a24(Y8) 10100 X5X6 X1D1 D1 D3 D3 R S a21 a25(Y3) 11001 X5X6 D1 D2 D5 T 2.2.3. Кодування станів Кодування станів буде проводитися за таким алгоритмом: 1. Кожному стану автомата аm (m = 1,2,...,M) ставиться у відповідність ціле число Nm, рівне числу переходів у стан аm (Nm дорівнює числу появ аm у поле таблиці ). 2. Числа N1, N2, ..., ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...


0 комментариев