Навигация
1 ПЗП
РМК
![]()
![]()
![]() FY П FX FA
FY П FX FA
СФМО
СФА Z1
y0.....yi к ОА
Z2
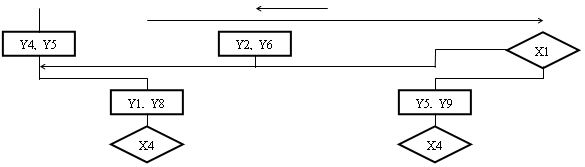
Мал.3.2. Структурна схема автомата з природною адресацією.
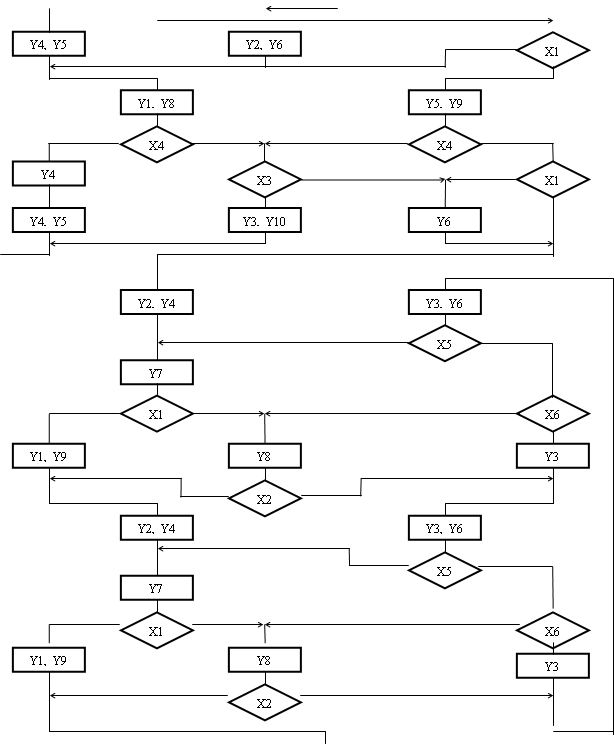
Для виключення подібних ситуацій вводять спеціальну вершину безумовного перходу (мал. 3.3). Дані вершини додаємо таким чином, щоб в одній точці сходилася будь-яка кількість переходів по “0" і тільки один по “1" або з операторної вершини. З врахуванням вказаних перетворень отримаємо перетворену ГСА (мал. 3.4).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
X0 0
1
Мал. 3.3. Вершина безумовного переходу.
3.3.Формування вмісту керуючої пам'яті.
На перетвореній ГСА виділимо мікрокоманди форматів ОМК, УМК1, УМК2. У результаті отримаємо 63 МК. Виконаємо їх адресацію. Для цього запишемо всі природні послідовності команд (ланцюжки вершин, перехід між якими здійснюється по “1" або через операторну вершину). У результаті отримаємо:
a1=[O1,O5]
a2=[ O2 ,O6 ,O7 ,O36 ,O48 ,O51 ,O55 ,O34 ,O47 ,O49 ,O56 ,O59 ,O12 ,O16 ,O45]
a3=[ O3 ,O9 ,O13 ,O18]
a4=[ O4 ,O10 ,O11]
a5=[ O8 ,O14 ,O20 ,O30 ,O32 ,O35]
a6=[ O60 ,O15 ,O21 ,O22]
a7=[ O17 ,O52 ,O57 ,O61 ,O62]
a8=[ O19 ,O28 ,O29]
a9=[ O23 ,O25 ,O27 ,O31 ,O37 ,O44 ,O43 ,O53 ,O54]
a10=[ O24 ,O26]
a11=[ O33]
a12=[ O38 ,O41 ,O42]
a13=[ O39 ,O40]
a14=[ O46]
a15=[ O50]
a16=[ O58]
a17=[ O63]
Перерахуємо в таблиці адресації (табл. 3.1) підряд всі послідовності a1-a17 і закодуємо їх R-розрядним кодом. R=]log2N[, N-кількість мікрокоманд (N=63, R=6). Закодуємо також оператори Yi, поставивши їм у відповідність п`ятирозрядний код. Будемо використовувати те ж кодування, що і в автоматі з ПА.(табл. 2.3., 2.4). У таблиці 3.2 відобразимо вміст керуючої пам'яті, заповнивши поля FX, FY, FA.
Таблиця 3.1. Таблиця 3.1.
(продовження)
Адресація МК.

| мк | А1А2А3А4А5А6 |
| O1 | 000000 |
| O5 | 000001 |
| O2 | 000010 |
| O6 | 000011 |
| O7 | 000100 |
| O36 | 000101 |
| O48 | 000110 |
| O51 | 000111 |
| O55 | 001000 |
| O34 | 001001 |
| O47 | 001010 |
| O49 | 001011 |
| O56 | 001100 |
| O59 | 001101 |
| O12 | 001110 |
| O16 | 001111 |
| O45 | 010000 |
| O3 | 010001 |
| O9 | 010010 |
| O13 | 010011 |
| O18 | 010100 |
| O4 | 010101 |
| O10 | 010110 |
| O11 | 010111 |
| O8 | 011000 |
| O14 | 011001 |
| O20 | 011010 |
| O30 | 011011 |
| O32 | 011100 |
| O35 | 011101 |
| O60 | 011110 |
| O15 | 011111 |
| O21 | 100000 |
| O22 | 100001 |
| O17 | 100010 |
| O52 | 100011 |
| O57 | 100100 |
| O61 | 100101 |
| O62 | 100110 |
Таблиця 3.2.
Вміст керуючої пам`яті автомата з природною адресацією.
| МК | Адреса | П | FY | Формула переходу | |
| FX | FA | ||||
| А1А2А3А4А5А6 | T1 | T2T3T4 | T5T6T7T8T9T10 | ||
| O1 | 000000 | 1 | 100 | 000010 | O1®щP1O2+P1O5 |
| O5 | 000001 | 1 | 000 | 010010 | O5®O9 |
| O2 | 000010 | 1 | 101 | 010001 | O2®щP2O3+P2O6 |
| O6 | 000011 | 1 | 110 | 011000 | O6®щP3O8+P3O7 |
| O7 | 000100 | 1 | 001 | 001001 | O7®щX1O34+X1O36 |
| O36 | 000101 | 0 | 010 | 000000 | O36®O48 |
| O48 | 000110 | 1 | 110 | 111110 | O48®щP3O63+P3O51 |
| O51 | 000111 | 0 | 000 | 010000 | O51®O55 |
| O55 | 001000 | 1 | 101 | 011110 | O55®щP2O60+P2O34 |
| O34 | 001001 | 0 | 000 | 111000 | O34®O47 |
| O47 | 001010 | 1 | 101 | 111011 | O47®щP2O46+P2O49 |
| O49 | 001011 | 1 | 010 | 111100 | O49®щX2O50+X2O56 |
| O56 | 001100 | 0 | 010 | 001000 | O56®O59 |
| O59 | 001101 | 1 | 100 | 101100 | O59®щP1O27+P1O12 |
| O12 | 001110 | 0 | 001 | 000000 | O12®O16 |
| O16 | 001111 | 1 | 100 | 110011 | O16®щP1O24+P1O45 |
| O45 | 010000 | 0 | 101 | 010000 | O45®K |
| O3 | 010001 | 1 | 110 | 010101 | O3®щP3O4+P3O9 |
| O9 | 010010 | 0 | 000 | 001000 | O9®O13 |
| O13 | 010011 | 1 | 100 | 100010 | O13®щP1O17+P1O18 |
| O18 | 010100 | 1 | 000 | 101100 | O18®щO27 |
| O4 | 010101 | 1 | 001 | 010010 | O4®щX1O9+X1O10 |
| O10 | 010110 | 1 | 010 | 001110 | O10®щX2O12+X2O11 |
| O11 | 010111 | 1 | 000 | 011111 | O11®O15 |
| O8 | 011000 | 0 | 001 | 101000 | O8®O14 |
| O14 | 011001 | 1 | 001 | 100111 | O14®щX1O19+X1O20 |
| O20 | 011010 | 0 | 000 | 101000 | O20®O30 |
| O30 | 011011 | 0 | 001 | 111000 | O30®O32 |
| O32 | 011100 | 1 | 110 | 000101 | O32®щP3O36+P3O35 |
| O35 | 011101 | 0 | 100 | 011000 | O35®K |
| O60 | 011110 | 0 | 001 | 011000 | O60®щO15 |
| O15 | 011111 | 0 | 000 | 110000 | O15®O21 |
| O21 | 100000 | 1 | 110 | 101010 | O21®щP3O23+P3O22 |
| O22 | 100001 | 0 | 101 | 100000 | O22®K |
| O17 | 100010 | 1 | 110 | 001110 | O17®щP3O12+P3O52 |
| O52 | 100011 | 0 | 000 | 110000 | O52®O57 |
| O57 | 100100 | 1 | 110 | 001001 | O57®щP3O34+P3O61 |
| O61 | 100101 | 1 | 011 | 000111 | O61®щX3O51+X3O62 |
| O62 | 100110 | 1 | 000 | 101100 | O62®O27 |
| O19 | 100111 | 0 | 001 | 110000 | O19®O28 |
Таблица 3.2.
(продовження)
| O28 | 101000 | 1 | 011 | 110101 | O28®щX3O33+X3O29 |
| O29 | 101001 | 1 | 000 | 101100 | O29®O27 |
| O23 | 101010 | 0 | 000 | 111000 | O23®O25 |
| O25 | 101011 | 0 | 001 | 001000 | O25®O27 |
| O27 | 101100 | 0 | 000 | 100000 | O27®O31 |
| O31 | 101101 | 1 | 100 | 110110 | O31®щP1O38+P1O37 |
| O37 | 101110 | 0 | 001 | 010000 | O37®O44 |
| O44 | 101111 | 1 | 001 | 010000 | O44®щX1O45+X1O43 |
| O43 | 110000 | 1 | 010 | 001110 | O43®щX2O12+X2O53 |
| O53 | 110001 | 0 | 000 | 001000 | O53®O54 |
| O54 | 110010 | 1 | 000 | 001100 | O54®O56 |
| O24 | 110011 | 1 | 110 | 101100 | O24®щP3O27+P3O26 |
| O26 | 110100 | 0 | 100 | 111000 | O26®K |
| O33 | 110101 | 0 | 100 | 000000 | O33®K |
| O38 | 110110 | 1 | 101 | 111001 | O38®щP2O39+P2O41 |
| O41 | 110111 | 1 | 110 | 111101 | O41®щP3O58+P3O42 |
| O42 | 111000 | 1 | 000 | 001110 | O42®щO12 |
| O39 | 111001 | 1 | 110 | 100011 | O39®щP3O52+P3O40 |
| O40 | 111010 | 1 | 000 | 011011 | O40®O30 |
| O46 | 111011 | 0 | 100 | 000000 | O46®K |
| O50 | 111100 | 0 | 100 | 000000 | O50®K |
| O58 | 111101 | 0 | 100 | 000000 | O58®K |
| O63 | 111110 | 0 | 100 | 000000 | O63®K |
Похожие работы
... булевої алгебри. Аналітичний спосіб задання булевих функцій займає особливе місце в проектуванні цифрових машин. Фактично, всі перетворення над булевими ф-ціями, необхідні для побудови цифрових машин, ведуться на аналітичному рівні. Розглянемо області визначення булевоі ф-ції. Як уже відмічалось, між двійковими наборами і двійковими числами існує взаємнооднозначна відповідність. Отже, існує 2n рі ...
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... a24(Y8) 10100 X5X6 X1D1 D1 D3 D3 R S a21 a25(Y3) 11001 X5X6 D1 D2 D5 T 2.2.3. Кодування станів Кодування станів буде проводитися за таким алгоритмом: 1. Кожному стану автомата аm (m = 1,2,...,M) ставиться у відповідність ціле число Nm, рівне числу переходів у стан аm (Nm дорівнює числу появ аm у поле таблиці ). 2. Числа N1, N2, ..., ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...


0 комментариев