Навигация
![]() СІ C
СІ C
![]()
![]()
![]() R
R
![]()
![]()
![]() “Reset” R щQ
“Reset” R щQ
Мал. 2.6. Базовий елемент регістра.
Схема РАМК містить 6 таких елементів, а схема РМК - 21. При побудові схеми сигнали щT1..щT21 будемо знімати з інверсних виходів елементів регістрів. Кількість мікросхем ПЗП визначимо за формулою: NПЗП=]R/3[, де R - розрядність мікрокоманди R=21, NПЗП=7. Для зберігання мікропрограми досить однієї лінійки ПЗП, оскільки QПЗП=8, тобто одна мікросхема розрахована на зберігання 256 трьохбітових комбінацій, а в нашому випадку потрібно тільки 38. При побудові схеми будемо записувати в РАМК інверсію адреси, а до ПЗП будемо подавати адресу з інверсних виходів елементів регістра, таким чином, ми заощадимо 6 елементів-інверторів у СФА. З врахуванням вищесказаного побудуємо схему автомата з примусовою адресацією мікрокоманд(мал. 2.7).
41
3.СИНТЕЗ АВТОМАТА З ПРИРОДНОЮ АДРЕСАЦІЄЮ МІКРОКОМАНД
3.1. Принцип роботи автомата.
При природній адресації микрокоманд існує три формата МК (мал. 3.1.).
![]()
![]()
П 1 FY m ОМК
![]()
![]()
![]()
![]()
![]()
![]() П 1 FX l1 FA r УМК1 П 1 Ж l1 FA r УМК2
П 1 FX l1 FA r УМК1 П 1 Ж l1 FA r УМК2
Мал.3.1. Формати мікрокоманд автомата з природною адресацією..
Тут формат ОМК відповідає операторній вершині, УМК1-умовній, а УМК2-вершині безумовного переходу. При подачі сигналу “пуск" лічильник ЛАМК обнуляється, і за сигналом СІ відбувається запис МК до регістра. СФМО формує відповідні МО при П=1 або видає на всіх виходах нулі при П=0. СФА в залежності від П і вмісту поля FX, формує сигнали Z1 і Z2. Сигнал Z1 дозволяє проходження синхроімпульсів на лічильний вхід ЛАМК, а Z2 дозволяє запис до лічильника адреси наступної МК з приходом синхроімпульсу.
Визначимо розрядність полів. l=]log2(L+1)[, де L-число умовних вершин. L=6, l=3
m=]log2T[ Т- число наборів мікрооперацій, що використовуються в ГСА, в нашому випадку Т=17, m=5
r=]log2 Q[, Q - кількість мікрокоманд.
3.2.Перетворення початкової ГСА.
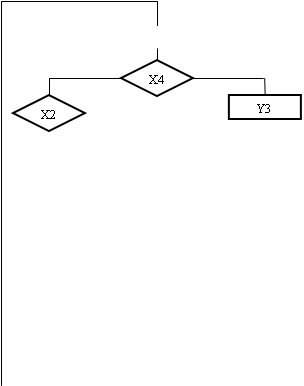
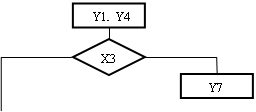
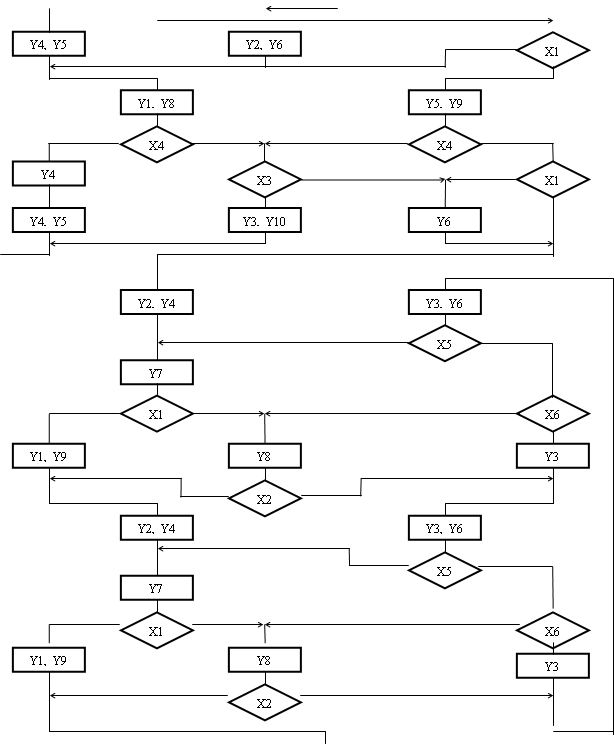
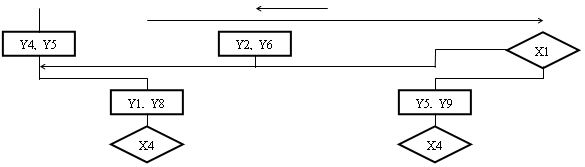
Перетворення буде полягати в тому, що до всіх операторних вершин, пов'язаних з кінцевою, вводиться сигнал y0, а між всіма умовними вершинами, які пов'язані з кінцевою, вводиться операторна вершина, що містить сигнал y0. Крім цього, в ГСА вводяться спеціальні вершини безумовного переходу X0, відповідні формату УМК2. Введення таких вершин необхідне для виключення конфліктів адресації мікрокоманд. У автоматі з природною адресацією (рис3.2.) при істинності(помилковість) логічної умови перехід здійснюється до вершини з адресою на одиницю великим, а при (помилковість)істинності ЛУ перехід відбувається за адресою, записаною в полі FA. У нашому випадку будемо додавати одиницю при істинності ЛУ або при переході з операторной вершини. Якщо в одній точці сходиться декілька переходів по “1" або з операторної вершини, то всі вершини з яких здійснювався перехід, повинні були б мати однакову (на одиницю меншу ) адресу, ніж наступна команда. Але це неможливо.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Z1 +1
Z1 +1
![]()
![]()
![]()
![]()

![]() сі Z2
А ЛАМК
сі Z2
А ЛАМК
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()

![]()
 “Пуск”
“Пуск”
Похожие работы
... булевої алгебри. Аналітичний спосіб задання булевих функцій займає особливе місце в проектуванні цифрових машин. Фактично, всі перетворення над булевими ф-ціями, необхідні для побудови цифрових машин, ведуться на аналітичному рівні. Розглянемо області визначення булевоі ф-ції. Як уже відмічалось, між двійковими наборами і двійковими числами існує взаємнооднозначна відповідність. Отже, існує 2n рі ...
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... a24(Y8) 10100 X5X6 X1D1 D1 D3 D3 R S a21 a25(Y3) 11001 X5X6 D1 D2 D5 T 2.2.3. Кодування станів Кодування станів буде проводитися за таким алгоритмом: 1. Кожному стану автомата аm (m = 1,2,...,M) ставиться у відповідність ціле число Nm, рівне числу переходів у стан аm (Nm дорівнює числу появ аm у поле таблиці ). 2. Числа N1, N2, ..., ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...


0 комментариев