Навигация
Перетворення початкової ГСА
4.2. Перетворення початкової ГСА.
Перетворення будемо виконувати двома етапами. На першому - введемо сигнал y0 до вершин, пов'язаних з кінцевою, якщо вершина умовна, то введемо
![]() +1
+1
![]()
![]() Z1
Z1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() СT
СT
![]() Z2
Z2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() S T & ПЗП
S T & ПЗП
![]()
![]() “Пуск”
“Пуск”
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 СІ
R РМК Y X A СФМО y0 .... yi Z1 СФА
СІ
R РМК Y X A СФМО y0 .... yi Z1 СФА
![]()
![]()
![]()
![]()
![]()
до ОА Z2
Мал.4.2. Структурна схема автомата з КА.
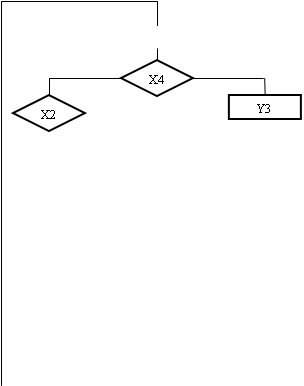
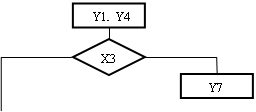
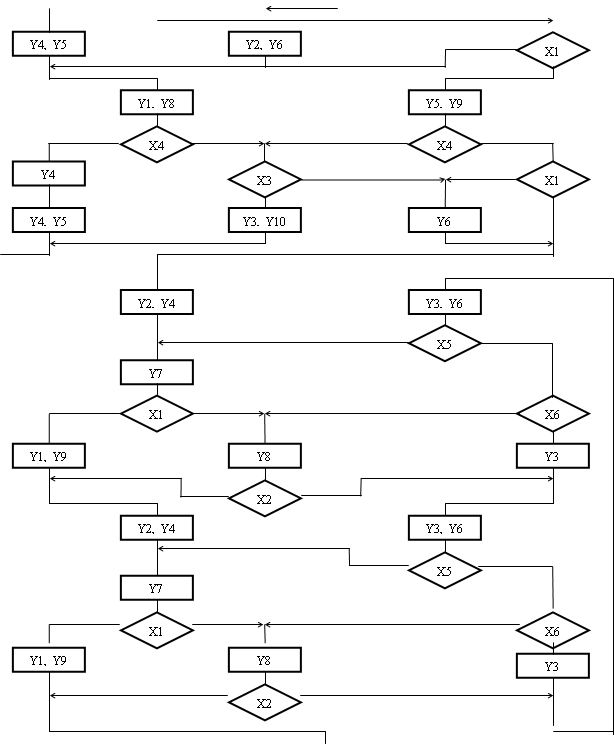
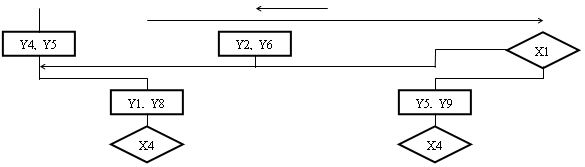
додаткову операторну вершину з сигналом y0. Крім того, введемо додаткові вершини безумовного переходу, виходячи з тих же міркувань, що і для автомата з природною адресацією. Будемо, однак, мати на увазі, що для автомата з КА перехід з операторної вершини прирівнюється до безумовного, тому в одній точці може сходитися будь-яка кількість безумовних переходів або переходів з операторних вершин і тільки один по істинності ЛУ, що перевіряється. На другому етапі виділимо мікрокоманди заданого формату, користуючись тими ж правилами, що і для автомата з ПА. З врахуванням вищесказаного отримаємо перетворену ГСА (мал. 4.3).
4.3.Формування вмісту керуючої пам'яті.
При формуванні вмісту керуючої пам'яті скористаємося тим же кодуванням наборів мікрооперацій і ЛУ, що і для автоматів з ПА і природною адресацією (табл. 2.3, 2.4). Для адресації мікрокоманд випишемо їх природні послідовності так само, як і для автомата з природною адресацією, враховуючи, що природним вважається тільки перехід по істинності ЛУ.
a1=[O1,O14]
a2=[ O2 ,O19 ,O18 ,O46 ,O6 ,O42 ,O43 ,O44 ,O9 ,O38 ]
a3=[ O3 ,O15 ,O17 ]
a4=[ O4 ,O5 ,O7,O8]
a5=[ O10 ]
a6=[ O11 ,O13]
a7=[ O12]
a8=[ O16,O29,O30,O25,O37,O35,O36]
a9=[ O20 ,O22 ]
a10=[ O21,O23]
a11=[ O26,O32,O33]
a12=[ O27 ,O24 ,O45]
a13=[ O34]
a14=[ O39]
a15=[ O40]
a16=[ O41]
a17=[ O28]
a18=[O31]
Перерахуємо в таблиці адресації (табл. 4.1) підряд всі послідовності a1-a18 і закодуємо їх R-розрядним кодом. R=]log2N[, N-кількість мікрокоманд(N=46, R=6). Закодуємо також оператори Yi, поставивши їм у відповідність п`ятирозрядний код. У таблиці 4.2 відобразимо вміст керуючої пам'яті, заповнивши поля FX, FY, FA.
Таблиця 4.1.
Адресація МК.
| мк | А1А2А3А4А5А6 |
| O1 | 000000 |
| O14 | 000001 |
| O2 | 000010 |
| O19 | 000011 |
| O18 | 000100 |
| O46 | 000101 |
| O6 | 000110 |
| O42 | 000111 |
| O43 | 001000 |
| O44 | 001001 |
| O9 | 001010 |
| O38 | 001011 |
| O3 | 001100 |
| O15 | 001101 |
| O17 | 001110 |
| O4 | 001111 |
| O5 | 010000 |
| O7 | 010001 |
| O8 | 010010 |
| O10 | 010011 |
| O11 | 010100 |
| O13 | 010101 |
| O12 | 010110 |
| O16 | 010111 |
| O29 | 011000 |
| O30 | 011001 |
| O25 | 011010 |
| O37 | 011011 |
| O35 | 011100 |
| O36 | 011101 |
| O20 | 011110 |
| O22 | 011111 |
| O21 | 100000 |
| O23 | 100001 |
| O26 | 100010 |
| O32 | 100011 |
| O33 | 100100 |
| O27 | 100101 |
| O24 | 100110 |
| O45 | 100111 |
| O34 | 101000 |
| O39 | 101001 |
| O40 | 101010 |
| O41 | 101011 |
| O28 | 101100 |
| O31 | 101101 |
Таблиця 4.2
Вміст керуючої пам`яті.
| № | A | FY | FX | FA |
| Оп. | A1A2A3A4A5А6 | T1T2T3T4T5T6 | T7T8T9 | T10T11T12T13T14T15 |
| O1 | 000000 | 000000 | 100 | 000010 |
| O14 | 000001 | 000000 | 000 | 001101 |
| O2 | 000010 | 000000 | 101 | 001100 |
| O19 | 000011 | 000000 | 110 | 011110 |
| O18 | 000100 | 000000 | 001 | 000111 |
| O46 | 000101 | 010000 | 110 | 101101 |
| O6 | 000110 | 000010 | 101 | 101100 |
| O42 | 000111 | 000111 | 101 | 101010 |
| O43 | 001000 | 000000 | 010 | 101011 |
| O44 | 001001 | 010001 | 100 | 011010 |
| O9 | 001010 | 001000 | 100 | 010100 |
| O38 | 001011 | 101010 | 000 | 000000 |
| O3 | 001100 | 000000 | 110 | 001111 |
| O15 | 001101 | 000001 | 100 | 010111 |
| O17 | 001110 | 000000 | 000 | 011010 |
| O4 | 001111 | 000000 | 001 | 001101 |
| O5 | 010000 | 000000 | 010 | 001010 |
| O7 | 010001 | 000110 | 110 | 010011 |
| O8 | 010010 | 101100 | 000 | 000000 |
| O10 | 010011 | 000111 | 000 | 010110 |
| O11 | 010100 | 000000 | 110 | 011010 |
| O13 | 010101 | 100111 | 000 | 000000 |
| O12 | 010110 | 001001 | 000 | 011010 |
| O16 | 010111 | 000000 | 110 | 001010 |
| O29 | 011000 | 000110 | 110 | 000111 |
| O30 | 011001 | 000000 | 011 | 000110 |
| O25 | 011010 | 000100 | 100 | 100010 |
| O37 | 011011 | 001010 | 001 | 001011 |
| O35 | 011100 | 000000 | 010 | 001010 |
| O36 | 011101 | 000001 | 000 | 001001 |
| O20 | 011110 | 001101 | 001 | 100000 |
| O22 | 011111 | 000101 | 000 | 100110 |
| O21 | 100000 | 001110 | 011 | 101001 |
| O23 | 100001 | 000000 | 000 | 011010 |
| O26 | 100010 | 000000 | 101 | 100101 |
| O32 | 100011 | 000000 | 110 | 101000 |
| O33 | 100100 | 000000 | 000 | 001010 |
| O27 | 100101 | 000000 | 110 | 011000 |
| O24 | 100110 | 001111 | 110 | 000101 |
| O45 | 100111 | 100011 | 000 | 000000 |
| O34 | 101000 | 100000 | 000 | 000000 |
Таблиця 4.2.
(продовження)
| O39 | 101001 | 100000 | 000 | 000000 |
| O40 | 101010 | 100000 | 000 | 000000 |
| O41 | 101011 | 100000 | 000 | 000000 |
| O28 | 101100 | 001011 | 000 | 010001 |
| O31 | 101101 | 100000 | 000 | 000000 |
4.4.Синтез схеми автомата.
При синтезі схеми скористаємося вже розробленими вузлами для автоматів з ПА і природною адресацією. СФА автомата з КА аналогічна СФА автомата з природною адресацією. Схеми СФМО, РМК аналогічні відповідним вузлам автомата з ПА (розд.2.4), а схема ЛАМК запозичена з автомата з природною адресацією (розд.3.4). Відмінність полягає лише в тому, що для РМК буде потрібно 15 базових елементів. Враховуючи вищесказане, побудуємо схему автомата з комбінованою адресацією мікрокоманд(мал. 4.4).
51
5. ПОРІВНЯЛЬНА ХАРАКТЕРИСТИКА АВТОМАТІВ.
5.1. Підрахунок апаратурних витрат.
Визначимо апаратурні витрати на кожний з автоматів. Оскільки синтез лічильника не був обов'язковим, то при визначенні апаратурних витрат будемо вважати його єдиним вузлом.
1. У автоматі з примусовою адресацією схема СФА містить 28 логічних елементів, СФМО - 57 ЛЕ, вузол запуску і схема “&" - 4 ЛЕ і, крім того, необхідно 6 елементів-інверторів для отримання сигналів щX1...щX3,щP1...щP3 Також потрібно 27 елементів для РАМК і РМК. Таким чином, сумарне число ЛЕ дорівнює 122. Для побудови РАМК і РМК також буде потрібно 27 тригерів. Кількість ПЗП- 7.
2. У автоматі з природною адресацією схема СФА містить 12 логічних елементів, СФМО - 68 ЛЕ, вузол скидання - 2 ЛЕ і, крім того, необхідно 6 елементів-інверторів для отримання сигналівщX1...щX3,щP1...щP3 і 10 елементів для РМК. Таким чином, сумарне число ЛЕ дорівнює 98. Для побудови РМК також буде потрібно 10 тригерів. Кількість ПЗП- 4. Схема також містить один лічильник.
3. У автоматі з комбінованою адресацією схема СФА містить 10 логічних елементів, СФМО - 57 ЛЕ, вузол запуску і схема “&" - 4 ЛЕ і, крім того, необхідно 6 елементів-інверторів для отримання сигналів щX1...щX3,щP1...щP3 і 15 елементів для РМК. Таким чином, сумарне число ЛЕ дорівнює 92. Для побудови РМК також буде потрібно 15 тригерів. Кількість ПЗУ- 5. Схема також містить один лічильник.
Складемо зведену таблицю витрат на синтезовані автомати.(табл. 5.1.)
Таблиця 5.1.
Апаратурні витрати для синтезованих автоматів.
| Тип автомата | Логічні елементи | Тригери | ПЗП | Лічильники |
| ПА | 122 | 27 | 7 | 0 |
| ПрА | 98 | 10 | 4 | 1 |
| КА | 92 | 15 | 5 | 1 |
5.2. Визначення автомата з мінімальними апаратурними витратами.
Заповнимо таблицю, де для кожного автомата знаком “+" відмітимо мінімальні витрати на даний тип елементів, а знаком “-" -немінімальні (табл. 5.2.).
Таблиця 5.2.
| Тип автомата | Логічні елементи | Тригери | ПЗП | Лічильники |
| ПА | - | - | - | + |
| ПрА | - | + | + | - |
| КА | + | - | - | - |
Як видно з таблиці 5.2., автомат з природною адресацією виграє по двом параметрам: по кількості тригерів і ПЗП.
Для підтвердження правильності вибору автомата застосуємо також оцінку за Квайном (за сумарною кількістю входів елементів). Будемо вважати кількість входів у ЛЕ - 4, у тригера - 4, у ПЗП -9 і у лічильника - 9. З врахуванням вищенаведених значень, для автомата з ПА показник оцінки складе - 659, для автомата з ПрА - 477, для автомата з КА- 482.
Як видно з приведених оцінок, автомат з примусовою адресацією далеко не оптимальний, а автомати з природною і комбінованою адресацією по витратах практично однакові, але все ж автомат з ПрА має деяку перевагу перед автоматом з КА. Таким чином, результатом проектування буде схема автомата з природною адресацією мікрокоманд.
Похожие работы
... булевої алгебри. Аналітичний спосіб задання булевих функцій займає особливе місце в проектуванні цифрових машин. Фактично, всі перетворення над булевими ф-ціями, необхідні для побудови цифрових машин, ведуться на аналітичному рівні. Розглянемо області визначення булевоі ф-ції. Як уже відмічалось, між двійковими наборами і двійковими числами існує взаємнооднозначна відповідність. Отже, існує 2n рі ...
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
... a24(Y8) 10100 X5X6 X1D1 D1 D3 D3 R S a21 a25(Y3) 11001 X5X6 D1 D2 D5 T 2.2.3. Кодування станів Кодування станів буде проводитися за таким алгоритмом: 1. Кожному стану автомата аm (m = 1,2,...,M) ставиться у відповідність ціле число Nm, рівне числу переходів у стан аm (Nm дорівнює числу появ аm у поле таблиці ). 2. Числа N1, N2, ..., ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...


0 комментариев