Навигация
2.4. Синтез схеми автомата.
Схема СФА являє собою мультиплексор, який в залежності від коду логічної умови, що перевіряється, передає на вихід Z1 значення відповідної ЛУ. При цьому сигнал Z2 завжди є інверсією сигналу Z1. Таким чином, отримаємо слідуючі вирази для Z1 і Z2:
Z1=X1щT7щT8T9+X2щT7T8щT9+X3щT7T8T9+P1T7щT8щT9+P2T7щT8T9+P3T7T8щT9
Z2=щZ1
або, звівши до заданого базису (4 АБО-НІ), отримаємо
Z1=щ щ(щ щ(A+B+C+D)+E+F), де
A=щ щ( X1щT7щT8T9)=щ(щX1+T7+T8+щT9)
B=щ щ( X2щT7T8щT9)=щ(щX2+T7+щT8+T9)
C=щ щ( X3щT7T8T9)=щ(щX3+T7+щT8+щT9)
D=щ щ( P1T7щT8щT9)=щ(щP1+щT7+T8+T9)
E=щ щ( P2T7щT8T9)=щ(щP2+щT7+T8+щT9)
F=щ щ( P3T7T8щT9)=щ(щP3+щT7+щT8+T9)
Інформація, що надходить на адресні входи ПЗП формується таким чином: Ai=A0iZ1+A1iZ2 або, приводячи до заданого базису, отримуємо Ai=щщ(щ(щA0i+щZ1)+щ(щA1i+щZ2)).
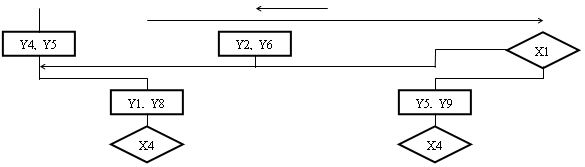
Синтезуємо тепер схему дешифратора, що формує сигнали мікрооперацій yi. Поява одиниці, відповідної кожному Y, відбувається при появі на вході дешифратора коду даного Y, тобто Yi=T2eЩT3eЩT4еЩT5еЩT6е, де еО{0,1} T0=щT, T1=T. Або приводячи до заданого базису, отримаємо: Yi=щ(щ щ(T2щe+T3щe+T4ще+T5ще)+T6ще). Таким чином, схема, що формує сигнал Y з п`ятирозрядного коду виглядає таким чином(мал. 2.4)
![]()
![]()
![]() T6щe
T6щe
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1 1 1 Yi
1 1 1 Yi
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
T2щe
![]()
Мал. 2.4. Схема формування сигналу Yi.
Враховуючи, що розряд T2 рівний “1" при формуванні тільки двох сигналів Y18 і Y20, то схему(мал. 2.4) будемо використовувати для формування Y1, Y20, для яких співпадають молодші чотири розряди та для Y18, для якого молодші чотири розряди співпадають з кодом порожньої операторної вершини. А для всіх інших Y схему можна спростити (мал.2.5.).
![]() T6щe
T6щe
![]()
![]()
![]()
![]() 1 Yi
1 Yi
![]()
![]() T3щe
T3щe
Мал.2.5. Спрощена схема формування сигналу Yi.
Згідно з наведеними схемами запишемо формули для всіх Yi.
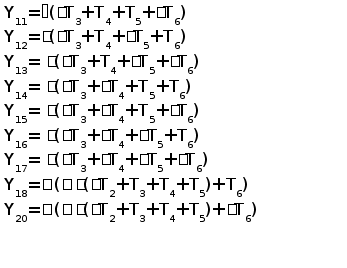
Y1=щ (щ щ(T2+T3+T4+T5)+щT6)
Y2= щ(T3+T4+щT5+T6)
Y3= щ(T3+T4+щT5+щT6)
Y5= щ(T3+щT4+T5+T6)
Y7= щ(T3+щT4+T5+щT6)
Y8= щ(T3+щT4+щT5+T6)
Y9= щ(T3+щT4+щT5+щT6)
Y10=щ(щT3+T4+T5+T6)
Сигнали мікрооперацій yj отримаємо, об'єднуючи по “або" виходи відповідні операторам Yi, в яких зустрічається МО yj. При цьому будемо користуватися таблицею
Таблиця 2.5.

Розподіл МО за мікро-
командами
| МО | номери МК |
| y1 | 1,2,3 |
| y2 | 1,7,17 |
| y3 | 5,10,14,20 |
| y4 | 5,10,13,15 |
| y5 | 2,8,10,12,15,18 |
| y6 | 3,7,9,12,13,15 |
| y7 | 7,11 |
| y8 | 11 |
| y9 | 1 |
| y10 | 1 |
| y11 | 3,14 |
| y12 | 2,12,16 |
| y13 | 5,8,17 |
| y14 | 16 |
| y15 | 8 |
| y16 | 7,16 |
| y17 | 9,11,12,14 |
| y18 | 10,14,15 |
| y19 | 2,10,12,15 |
| y20 | 3,11,13 |
| y21 | 13 |
| y22 | 14 |
| y23 | 15 |
| y24 | 16 |
| y25 | 17 |
| y27 | 20 |
| y28 | 20 |
| y29 | 8 |
| y30 | 5 |
На наступному етапі синтезуємо схеми РАМК і РМК, використовуючи щRщS тригери. Скористаємося класичним методом синтезу регістрів і заповнимо слідуючу таблицю (табл. 2.6.).
Таблиця 2.6.
Синтез РАМК та РМК

| С | Ai | Qt | Qt+1 | Ct | щR | щS |
| 0 | 0 | 0 | 0 | 0 | * | * |
|
| 0 | 1 | 1 | 0 | * | * |
|
| 1 | 0 | 0 | 0 | * | * |
| 0 | 1 | 1 | 1 | 0 | * | * |
| 1 | 0 | 0 | 0 | 1 | * | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | * |
У результаті отримаємо слідуючу схему для базового елементу РАМК та РМК (мал.2.6).

![]()
![]()
![]()
![]() Ai
Ai
![]()
![]()
![]()
![]()
Похожие работы
... булевої алгебри. Аналітичний спосіб задання булевих функцій займає особливе місце в проектуванні цифрових машин. Фактично, всі перетворення над булевими ф-ціями, необхідні для побудови цифрових машин, ведуться на аналітичному рівні. Розглянемо області визначення булевоі ф-ції. Як уже відмічалось, між двійковими наборами і двійковими числами існує взаємнооднозначна відповідність. Отже, існує 2n рі ...
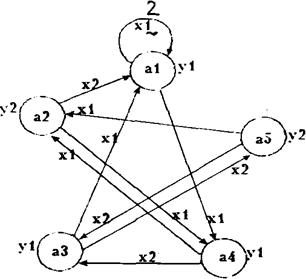
... определенным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены для всех пар переходов (xi,aj). Частичным называется абстрактный цифровой автомат, у которого функция переходов или функция выходов, или обе эти функции определены не для всех пар переходов (xi,aj). Абстрактный цифровой автомат называется инициальным, если на ...
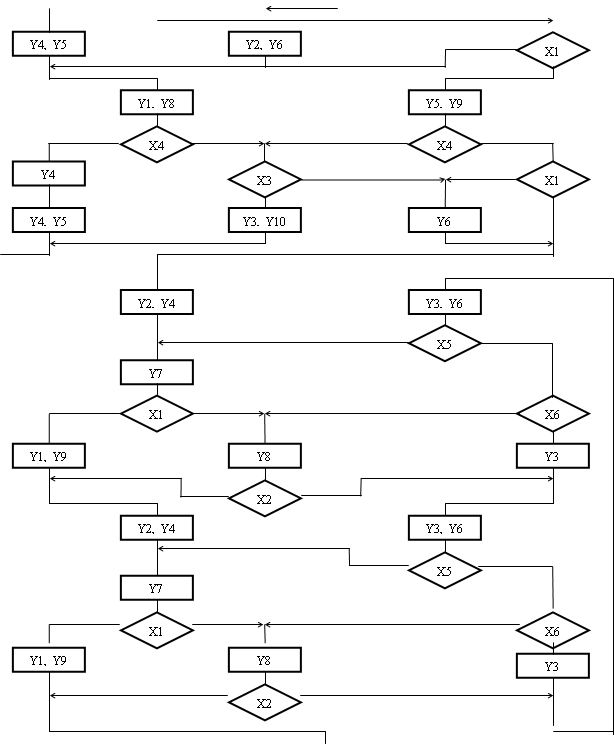
... a24(Y8) 10100 X5X6 X1D1 D1 D3 D3 R S a21 a25(Y3) 11001 X5X6 D1 D2 D5 T 2.2.3. Кодування станів Кодування станів буде проводитися за таким алгоритмом: 1. Кожному стану автомата аm (m = 1,2,...,M) ставиться у відповідність ціле число Nm, рівне числу переходів у стан аm (Nm дорівнює числу появ аm у поле таблиці ). 2. Числа N1, N2, ..., ...
... состоянии am. Рассмотренные выше абстрактные автоматы можно разделить на: 1) полностью определенные и частичные; 2) детерминированные и вероятностные; 3) синхронные и асинхронные; Полностью определенным называется абстрактный цифровой автомат, у которого функция переходов и функция выходов определены для всех пар ( ai, zj). Частичным называется абстрактный автомат, у которого функция ...


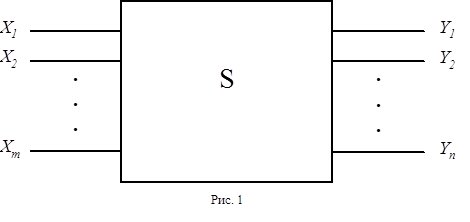
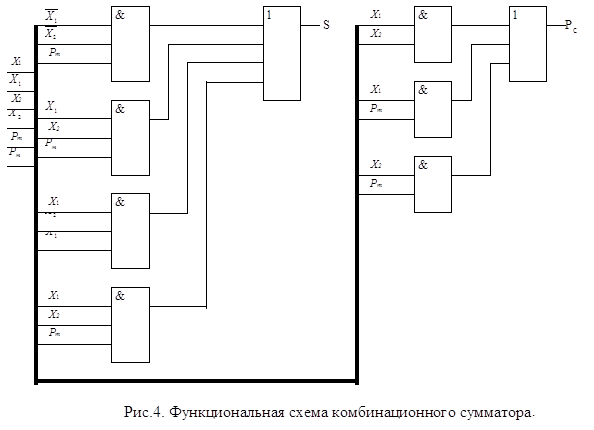
0 комментариев