Навигация
Алгоритм расчёта
3.1.1 Алгоритм расчёта
Параметры инструмента, зависящие от угла наклона зубьев b.
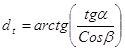
![]()
![]()
![]() .
.
1). Радиусы делительных окружностей:
![]()
2). Радиусы основных окружностей:
![]()
Расчётные коэффициенты смещения х1 и х2 для рассчитываемой передачи должны прежде всего обеспечивать отсутствие подреза (хmin) и заострения зубьев (хmax), а также гарантировать минимально допустимую величину коэффициента перекрытия. Следовательно, должно соблюдаться условие хtmin<x1,2<xmax.
3). Минимальное число зубьев на нулевом колесе, которое можно нарезать без подреза:
![]()
4). Минимальные коэффициенты смещения:
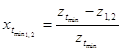
Максимальный коэффициенты смещения не может быть определён непосредственно, отсутствие заострения может быть выявлено после подсчёта толщины зуба по окружности вершин и удовлетворено при условии: ![]() .
.
5). Выбор коэффициента смещения:
Коэффициент смещения х2 выбирается по ГОСТ-18532-83.
6). Угол зацепления передачи:
Решается с помощью подпрограммы RIMT
7). Коэффициент воспринимаемого смещения:
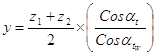
8). Коэффициент уравнительного смещения:
![]()
9). Радиусы делительных окружностей:
![]()
10). Межосевое расстояние передачи:
![]()
11). Радиусы окружностей вершин:
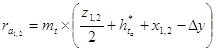
12). Радиусы окружностей вершин:
![]()
13). Высота зубьев колёс:
![]()
14). Толщина зубьев по дугам делительных окружностей:
![]()
15). Углы профиля на окружностях вершин зубьев колёс:
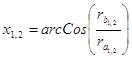
16). Толщина зубьев на окружностях вершин зубьев колёс:
![]()
Качественные показатели передачи.
1). Коэффициент перекрытия зубчатой передачи:
![]() , где
, где
![]() ,
,
![]()
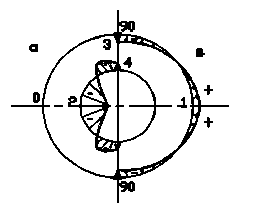
2). Коэффициент скольжения:
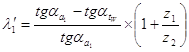
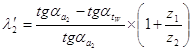
3.1.4 Анализ результатов расчёта на ЭВМ.
Для построения картины зубчатого зацепления необходимо выбрать значения параметров зубчатого зацепления, приведенные на стр. 19 в распечатке расчётов на ЭВМ. Для этого нужно определить величину х1 – расчётного коэффициента смещения.
3.2 Построение геометрической картины эвольвентного зубчатого зацепления.3.2.1 Откладываем межосевое расстояние аW=O1O2 – сумму радиусов начальных окружностей.
3.2.2 Проводим радиусы выступов (ra1, ra2), ножек (rf1, rf2), основных (rb1, rb2) и делительных (r1, r2) окружностей.
3.2.3 Проверяем радиальный зазор с=с*´m, где с*=0,25.
3.2.4 Проводим радиусы основных окружностей и отмечаем на них точки N1 и N2, O1N1 расположится под углом к O1O2 - aWt=25° 04'01", O2N2 - aWt=25° 04'01".
3.2.5 Через точки N1 и N2 проводим общую касательную к окружностям rb1 и rb2. N1N2 – есть теоретическая линия зацепления.
3.2.6 Расстояние N1Р по теоретической линии зацепления N1N2 делим на 4 равные части. Такие же отрезки откладываем за точку N1 и получаем точки 1-6.
3.2.7 Из точки 3 раствором циркуля "3-Р" делаем на rb1 засечку – точка q. Дугу основной окружности rb1 – qN1 делим на 4 равные части и продолжаем деления за точку N1, получаем точки 1,2,3,4,5.
3.2.8 Точки на основной окружности соединяем с центром вращения шестерни.
3.2.9 Перпендикулярно радиусам проводим касательные к основной окружности в каждой точке.
3.2.10 Замеряем расстояние по теоретической линии зацепления: 1Р, 2Р, …, 6Р и из точек 1', 2', …, 6' делаем засечки на соответствующих касательных.
3.2.11 Соединяем полученные точки на касательных, получаем эвольвенту 1-го колеса.
3.2.12 Строим ножку зуба. Для этого точку q соединяем с центром вращения 1-го колеса и радиусом rf=0,38´m делаем скругления.
3.2.13 Отложив толщину зуба по дуге делительной окружности S1, строим левый профиль зуба. Разделив толщину зуба пополам, получаем ось симметрии зуба.
3.2.14 Отложив шаги Рt на хорде делительной окружности влево и вправо, получаем оси 2-го и 3-го зубьев и строим три зуба второго колеса.
3.2.15 Определяем длины активной линии зацепления АВ. Расстояния по теоретической линии зацепления N1N2 между точками пересечения окружностей выступов каждого колеса с теоретической линией зацепления – есть практическая линия зацепления.
3.2.16 Определяем дуги зацепления. Через точки теоретической линией зацепления Н1 и Н2 проводим правый профиль зуба первого колеса и левый профиль второго колеса.
3.2.17 Определяем рабочие части боковых профилей зубьев. Радиусами О1Н2 иО2Н1 проводим дуги до пересечения с боковыми профилями зубьев.
3.3 Синтез планетарного редуктора.3.3.1 Выбор числа зубьев методом обращения движения.
![]() Þ
Þ ![]()
принимаем z4=40, тогда z6=2,8´40=112>85 – целое число. Число z5 определяем из условия соседства: ![]() >17 – целое число.
>17 – целое число.
3.3.2 Проверка условия сборки.
Приняв z4=40, z5=36, z6=112, проверяем передачу на условие сборки без натягов (при k=4; p=0):
![]() – целое число, условие соблюдается.
– целое число, условие соблюдается.
Похожие работы
... четвертого колеса к третьему; отношение модулей зубчатых колес первой ступени к второй. 3. Исследование качественных характеристик внешнего эвольвентного зацепления Зубчатые передачи являются наиболее распространенным видом механических передач. В зависимости от условий эксплуатации при проектировании зубчатых передач учитываются различные факторы, влияющие на повышение их прочности, ...
... двигателя и улучшения его показателей в соответствии с уровнем развития техники. ЛИТЕРТУРА 1. Б.Е.Железко, В.М.Адамов, И.К.Русецкий, Г.Я.Якубенко / Расчет и конструирование автомобильных и тракторных двигателей (Дипломное проектирование): Учебное пособие для вузов / Мн.:"Высшая школа", 1987 г. 2. А.И.Колчин, В.П.Демидов / Расчет автомобильных и тракторных двигателей. Учебник для ВУЗов / ...
... электроэнергии, воды, местные вентиляционные отсосы, нахождения аптечки и средств пожаротушения. 6. Конструкторская разработка 6.1 Анализ существующих конструкций и приспособлений для обкатки и испытания двигателей внутреннего сгорания Приработка и испытания двигателей внутреннего сгорания производятся на обкаточно-тормозных стендах переменного тока, включающих устройство для вращения ...
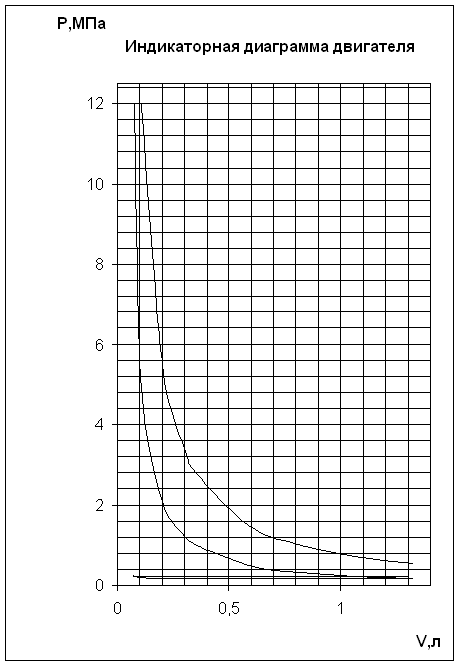
... и точки расширения соединяем плавными кривыми. После этого достраиваем процессы газообмена. Полученная индикаторная диаграмма двигателя внутреннего сгорания дизеля MAN изображена на рисунке 14.1. Рисунок 14.1 - Индикаторная диаграмма ДВС MAN. Выводы Результаты расчетов и общепринятые границы изменения расчетных параметров сводим в таблицу. Таблица - Результаты расчетов. НАЗВАНИЕ ...

0 комментариев