Навигация
Развитие понятия числа
1.3 Развитие понятия числа
При счете отдельных предметов единица есть наименьшее число; делить ее на доли не нужно, а часто и невозможно (при счете камней прибавление к двум камням половины третьего дает три камня, а не два с половиной). Однако делить единицу на доли приходится уже при грубых измерениях величин, например при измерении длины шагами (два с половиной шага и т.д.). Поэтому уже в отдаленные эпохи создалось понятие дробного числа.
Так, в вавилонской системе мер веса (и денег) 1 талант составлял 60 мин, а одна мина – 60 шекелей. Соответственно с этим в вавилонской математике широко употреблялись шестидесятиричные дроби. В древнеримской весовой (и денежной) системе 1 асс делился на 12 унций; сообразно с этим римляне пользовались двенадцатиричными дробями.
Наши «обыкновенные дроби» широко употреблялись древними греками и индийцами. Правила действий с дробями, изложенные индийским ученым Брамагуптой (VIII век н.э.), лишь немногим отличаются от наших. Наша запись дробей тоже совпадает с индийской; только дробной черты индийцы не писали; греки записывали сверху знаменатель, а снизу числитель.
Индийской обозначение дробей и правила действий над ними были усвоены в IX веке в мусульманских странах благодаря узбекскому ученому Мухаммеду Хорземскому (аль-Хваризми). Они были перенесены в Западную Европу итальянским купцом и ученым Леонардо Фибоначчи из Пизы (XIII век).
Наряду с «обыкновенными» дробями до XVII века применялись (преимущественно в астрономии) шестидесятиричные дроби. Они были вытеснены десятичными дробями, введенными голландским купцом и выдающимся инженером-ученым Симоном Стевином (1548 - 1620).
В дальнейшем оказалось необходимым еще больше расширить понятие числа; последовательно появились числа иррациональные, отрицательные и комплексные.
Довольно поздно к семье чисел присоединился нуль. Первоначально слово «нуль» означало отсутствие числа (буквальный смысл латинского слова nullum – «ничто»). Для того чтобы это «ничто» считать числом, появились основания лишь в связи с рассмотрением отрицательных чисел.
1.4 Системы нумерации некоторых народов
1.4.1 Древнегреческая нумерация
В
древнейшее
время в Греции
была распространена
т.н. аттическая
нумерация.
Числа 1, 2, 3, 4 обозначались
черточками ![]() ,
, ![]() ,
,![]() ,
,![]() .
Число 5 записывалось
знаком
.
Число 5 записывалось
знаком ![]() (древнее начертание
буквы «пи», с
которой начинается
слово «пенте»
– пять); числа
6, 7, 8, 9 обозначались
(древнее начертание
буквы «пи», с
которой начинается
слово «пенте»
– пять); числа
6, 7, 8, 9 обозначались ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Число 10 обозначалось
.
Число 10 обозначалось ![]() (начальной
буквой слова
«дека» – десять).
Числа 100, 1000 и 10000
обозначались
(начальной
буквой слова
«дека» – десять).
Числа 100, 1000 и 10000
обозначались ![]() ,
, ![]() ,
, ![]() .
Числа 50, 500, 5000 обозначались
комбинациями
знаков 5 и 10, 5 и
100, 5 и 1000. Общую запись
чисел в аттической
нумерации
иллюстрирует
пример 1.1.
.
Числа 50, 500, 5000 обозначались
комбинациями
знаков 5 и 10, 5 и
100, 5 и 1000. Общую запись
чисел в аттической
нумерации
иллюстрирует
пример 1.1.
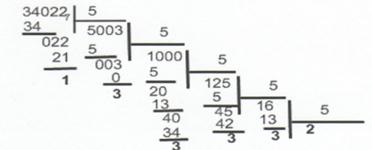
Пример 1.1 Запись чисел в аттической системе счисления
|
|
|
|
|
|
|
|
|
|
|
|
В третьем веке до н.э. аттическая нумерация была вытеснена так называемой ионийской системой. В ней числа 1 – 9 обозначались первыми девятью буквами алфавита; числа 10, 20, 30, … , 90 – следующими девятью буквами; числа 100, 200, … , 900 – последними девятью буквами.
Таблица 1.1 Обозначение чисел в ионийской системе нумерации
| Обозна- Чение | Название | Значе-ние | Обозна-чение | Название | Значе-ние | Обозна-чение | Назва-ние | Значе-ние |
|
| Альфа | 1 |
| Йота | 10 |
| Ро | 100 |
|
| Бета | 2 |
| Каппа | 20 |
| Сигма | 200 |
|
| Гамма | 3 |
| Лямбда | 30 |
| Тау | 300 |
|
| Дельта | 4 |
| Мю | 40 |
| Ипсилон | 400 |
|
| Эпсилон | 5 |
| Ню | 50 |
| Фи | 500 |
| Фауб | 6 |
| Кси | 60 |
| Хи | 600 | |
|
| Дзета | 7 |
| Омикрон | 70 |
| Пси | 700 |
|
| Эта | 8 |
| Пи | 80 |
| Омега | 800 |
|
| Тэта | 9 | Коппа | 90 | Сампи | 900 |
Следует отметить, что буквы «фау», «коппа» и «сампи» отсутствуют в современном греческом алфавите.
Для обозначения тысяч и десятков тысяч пользовались теми же цифрами с добавлением особого значка ` сбоку.
Для отличия цифр от букв, составлявших слова, писали черточки над цифрами. Обозначение чисел в ионийской нумерации представлены в таблице 1.1, а примеры написания различных чисел в примере 1.2.
Пример 1.2 Запись чисел в ионийской системе счисления
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Такую же алфавитную нумерацию имели в древности евреи, арабы и многие другие народы Ближнего Востока.
Похожие работы
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...
... представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа. Позиционные системы счисления В ...
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п





0 комментариев