Навигация
Комбинация знаковых цифр мантиссы показывает, что сумма денормализована влево (всегда только на один разряд)
4. Комбинация знаковых цифр мантиссы показывает, что сумма денормализована влево (всегда только на один разряд)
Произведем нормализацию суммы вправо
![]()
![]()
[m3]мод= 10, 111101 1,0111101
доп
Робщ = 0,101 + 0,001 = 0,110
Далее переводим сумму в прямой код и производим округление ее мантиссы до пяти разрядов.
О![]()
![]()
![]() твет:
[X3]пр
= 0 110 ; 1,1000011 ~
0 100; 1, 10001
твет:
[X3]пр
= 0 110 ; 1,1000011 ~
0 100; 1, 10001
порядок мантисса
Умножение чисел с фиксированной запятойНаиболее просто умножение выполняется в прямом коде, независимо от того, являются ли операнды целыми или дробными числами. В машинах с фиксированной запятой оно реализуется в два этапа.
1. Определяется знак произведения с помощью сложения знаковых цифр сомножителей по модулю два, где нуль соответствует плюсу, а единица - минусу:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0
Вручную это эквивалентно:
(+) (+) = (+); (+) (-) = (-); (-) (+) = (-); (-) (-) = (+).
2. Производиться перемножение модулей сомножителей, затем в случае необходимости округление полученного модуля произведения, после чего к модулю результата приписывается его знак, определенный на первом этапе.
Умножение производится по обычным правилам арифметики согласно двоичной таблицы умножения. Произведение модулей |Х3| = |Х1| * |Х2| двух (например дробных) чисел, где множитель Х2 = Х21 2-1 + Х22 2-2 +…+ Х2n2-n, чаще всего вычисляется как сумма так называемых частичных произведений:
n
/Х3/ = /Х/ Х2i 2-i
i=1
В машинах может быть реализовано как умножение, начинающееся с младшей цифры множителя (наиболее привычный способ), так и умножение, начинающееся со старшей цифры множителя. При умножении вручную в первом случае частичные произведения сдвигаются влево, во втором - вправо.
ПРИМЕР. Перемножить числа [X1]пр = 0,1010 и [X2]пр = 1,1101
Решение.
1. Определяем знак произведения 0 + 1 = 1.
2. Перемножим модули операндов, порядок перемножения определяется нумерацией цифр множителя:
1-й способ
0,1010 0,1010
х 0,1101 х 0,1101
![]()
![]() 4,3,2,1 номера цифр
множителя 1,2,3,4
4,3,2,1 номера цифр
множителя 1,2,3,4
1010 1010
0000 1010
+1010 + 0000
1010 1010
0,10000010 0,10000010
После округления приписываем к модулю знак произведения, полученный на первом этапе умножения.
О![]() твет:
[X3]пр
= 1,0000010 ~ 1,10000.
твет:
[X3]пр
= 1,0000010 ~ 1,10000.
Первый способ часто называют умножением младшими разрядами вперед, а второй - умножением старшими разрядами вперед.
Умножение чисел с плавающей запятойЕсли имеем два сомножителя, заданные в нормальной форме Х1 = m1 10p1 и Х2 = m2 10p2, то их произведение определяется следующим образом:
Х1 Х2 = m1 m2 10p1+р2.
Анализ этого соотношения показывает, что умножение чисел в машинах с плавающей запятой производится в четыре этапа:
1. Определение знака произведения путем сложения по модулю два знаковых цифр мантисс сомножителей.
2. Перемножение модулей мантисс сомножителей по правилам для дробных чисел с фиксированной запятой.
3. Определение порядка произведения путем алгебраического сложения порядков сомножителей с использованием либо дополнительного, либо обратного модифицированного кода.
4. Нормализация результата и округление мантиссы в случае необходимости. Поскольку сомножители обязательно являются нормализованными числами, то де нормализация произведения возможна только на разряд и только вправо.
ПРИМЕР. Перемножить числа с плавающей запятой.
Множимое [X1]пр = 0 101; 1,10101
Множитель [X2]пр = 0 100; 1,11001
Решение.
Похожие работы
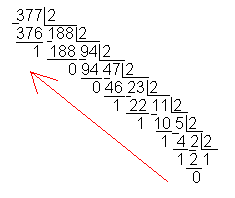
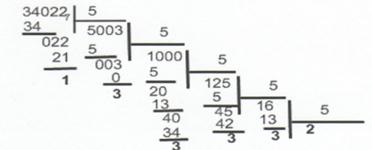
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...
... представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа. Позиционные системы счисления В ...
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п


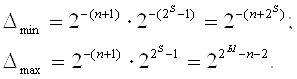



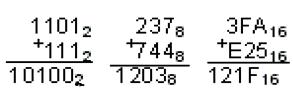
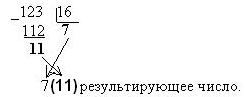
0 комментариев