Навигация
Двоичное вычитание
4.3.2 Двоичное вычитание
Вычитание в двоичной системе выполняется аналогично вычитанию в десятичной системе счисления. При необходимости, когда в некотором разряде приходится вычитать единицу из нуля, занимается единица из следующего старшего разряда. Если в следующем разряде нуль, то заем делается в ближайшем старшем разряде, в котором стоит единица. При этом следует понимать, что занимаемая единица равна двум единицам данного разряда, т. е. вычитание выполняется по следующему правилу:
Пример
4.7 Вычитание
двоичных чисел ![]() и
и ![]()
| – | 11010, | 1011 | |
| 1101, | 01111 | ||
| 1101, | 00111 | ||
Конечно, математически вычитание выполнить несложно. Однако, если поступать таким образом, то к примеру в ЭВМ придется для выполнения сложения и вычитания иметь два блока: сумматор и вычитатель. Поэтому поступают следующим образом: вычитание можно представить как сложение положительного и отрицательного чисел, необходимо только подходящее представление для отрицательного числа.
Рассмотрим четырехразрядный десятичный счетчик, какие в автомобиле отсчитывают пройденный путь. Пусть он показывает число 2, если вращать его в обратном направлении, то сначала появится 1, затем 0, после 0 появится число 9999. Сложим, к примеру, 6 с этим числом:
| + | 6 | ||
| 9999 | |||
| 10005 | |||
Если пренебречь
единицей переноса
и считать 9999
аналогом –1, то
получим верный
результат: ![]() .
.
Число 9999 называется десятичным дополнением числа 1. Таким образом, в десятичной системе счисления отрицательные числа могут быть представлены в форме десятичного дополнения, а знак минус можно опустить.
Двоичное дополнение числа определяется как то число, которое будучи прибавлено к первоначальному числу, даст только единицу переноса в старшем разряде.
Пример
4.8 Двоичное
дополнение
числа ![]()
| + | 010101111 | – число |
| 101010001 | – двоичное дополнение | |
| 1000000000 | – сумма | |
| – единица переноса | ||
Для получения двоичного дополнения необходимо:
получить обратный код, который образуется инвертированием каждого бита:
| 010101111 | – число |
| 101010000 | – обратный код |
прибавить к обратному коду единицу, образовав таким образом дополнительный код:
| + | 101010000 | – обратный код |
| 1 | ||
| 101010001 | – дополнительный код |
Пример 4.9 Вычитание в дополнительном коде
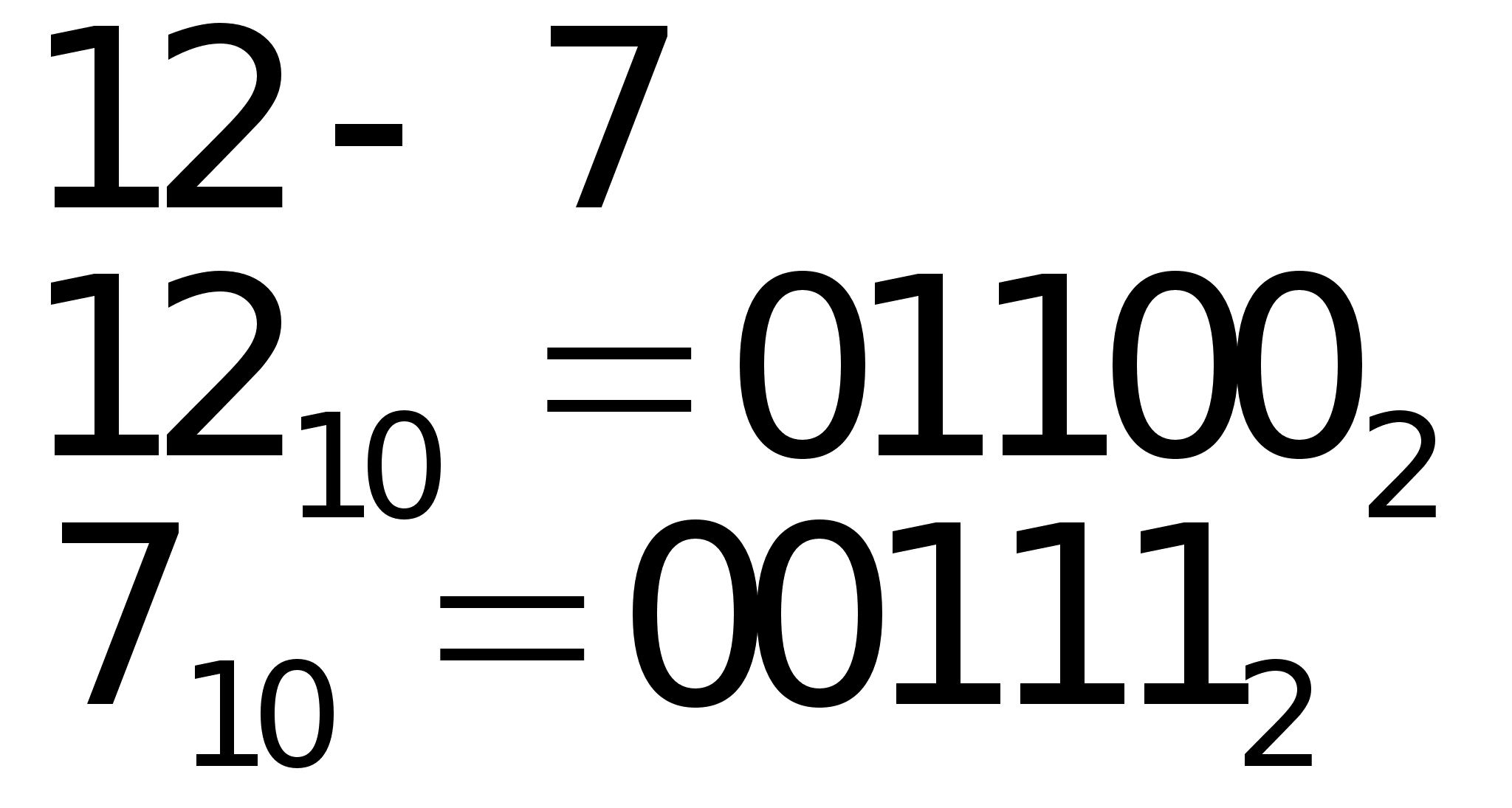
![]() – обратный
код,
– обратный
код,
![]() – дополнительный
код.
– дополнительный
код.
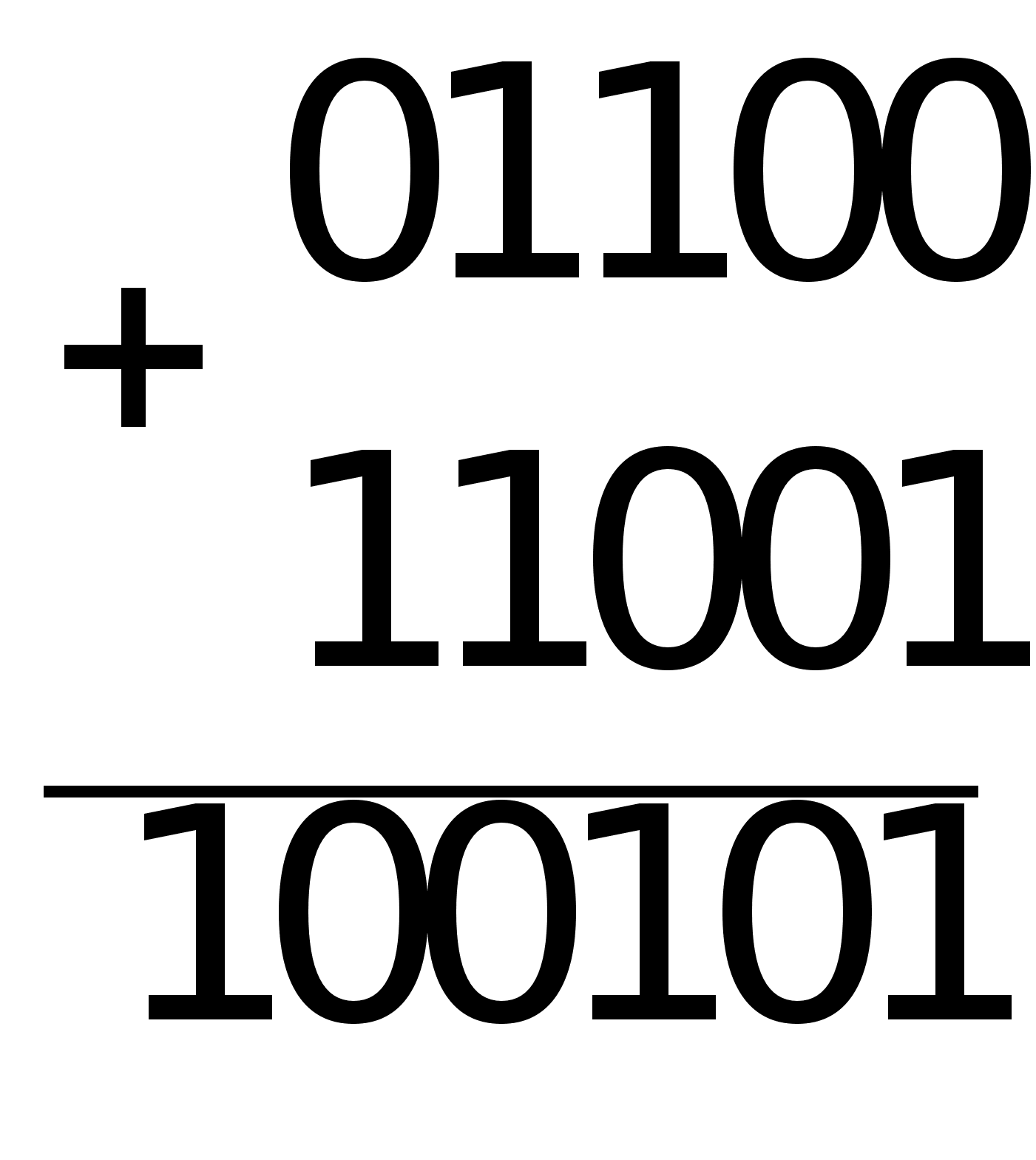
1001012=510 (верно).
4.3.3 Двоичное умножение
Умножение двух двоичных чисел выполняется так же, как и умножение десятичных. Сначала получаются частичные произведения и затем их суммируют с учетом веса соответствующего разряда множителя.
Отличительной особенностью умножения в двоичной системе счисления является его простота, обусловленная простотой таблицы умножения. В соответствии с ней, каждое частичное произведение или равно нулю, если в соответствующем разряде множителя стоит нуль, или равно множимому, сдвинутому на соответствующее число разрядов, если в соответствующем разряде множителя стоит единица. Таким образом, операция умножения в двоичной системе сводится к операциям сдвига и сложения.
Умножение производится, начиная с младшего или старшего разряда множителя, что и определяет направление сдвига. Если сомножители имеют дробные части, то положение запятой в произведении определяется по тем же правилам, что и для десятичных чисел.
Пример
4.10 Умножение
двоичных чисел ![]() и
и ![]()
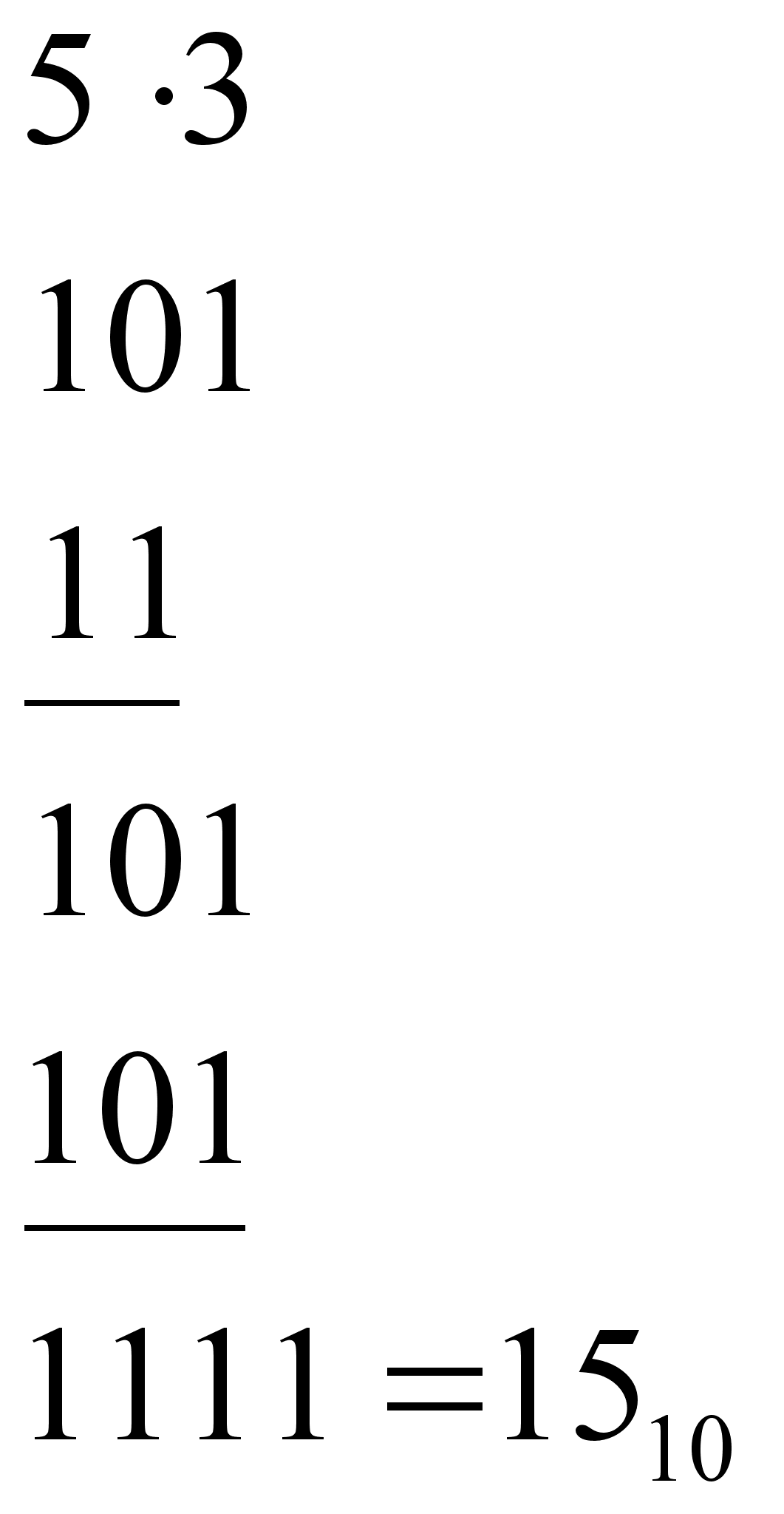
Похожие работы
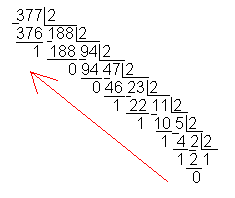
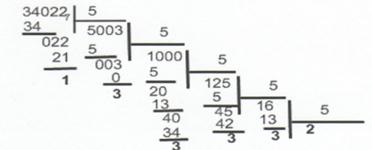
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...
... представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа. Позиционные системы счисления В ...
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п





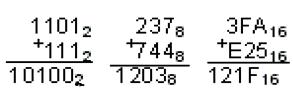
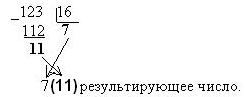
0 комментариев