Навигация
Знак произведения 1 + 0 = 1
1. Знак произведения 1 + 0 = 1.
2. Перемножаем модули мантисс:
1-й шаг ,0000 0000 - нулевая сумма
![]() +,0000 1010 - 1-е
частичное
произведение
+,0000 1010 - 1-е
частичное
произведение
2-й шаг ,0000 1010 - 2-я сумма
+ ,0000 0000 - 2-е частичное произведение
3-й шаг ,0000 1010 - 3-я сумма
+ ,0010 1000 - 3-е частичное произведение
4-й шаг ,0011 0010 - 4-я сумма
+ ,0101 0000 - 4-е частичное произведение
, 1000 0010 - модуль произведения мантисс.
Находим порядок произведения:
[р1]мод= 00,101доп
[р2]мод= 11,101
доп
![]()
[р3]мод= 100, 010
![]() доп
доп
![]()
теряется
Производим округление мантиссы произведения.
О![]()
![]() твет:
[X3]пр = [Х1
Х2]пр
= 0 010 ; 1 100
твет:
[X3]пр = [Х1
Х2]пр
= 0 010 ; 1 100
порядок мантисса
Прямой, обратный и дополнительный коды. Модифицированный код.
В![]() ведем
определение
прямого, обратного
и дополнительного
кодов. Рассмотрим
двоичное число
ведем
определение
прямого, обратного
и дополнительного
кодов. Рассмотрим
двоичное число ![]() В соответствии
с изложенным
выше число R
кодируется
следующим
образом:
В соответствии
с изложенным
выше число R
кодируется
следующим
образом:
0
![]()
![]()
R= 1
![]()
![]()
и![]() ли,
в более общем
случае, если
ли,
в более общем
случае, если ![]() ,
,
0
![]()
![]()
R=
![]()
![]()
![]()
Так
как ![]() ,
эти соотношения
можно переписать
таким образом:
,
эти соотношения
можно переписать
таким образом:
![]()
![]() ,
, ![]()
![]() =
=
![]()
![]()
Представление
чисел в соответствии
с данной формулой
называется
прямым кодом
числа ![]()
Е![]() сли
сли ![]() ,
то формула
,
то формула ![]() перепишется
в таком виде:
перепишется
в таком виде:
![]() ,
, ![]()
![]() =
=
![]()
![]()
Аналогичным образом кодируются и числа, модуль которых не меньше единицы.
Пример: Записать числа в прямом коде:
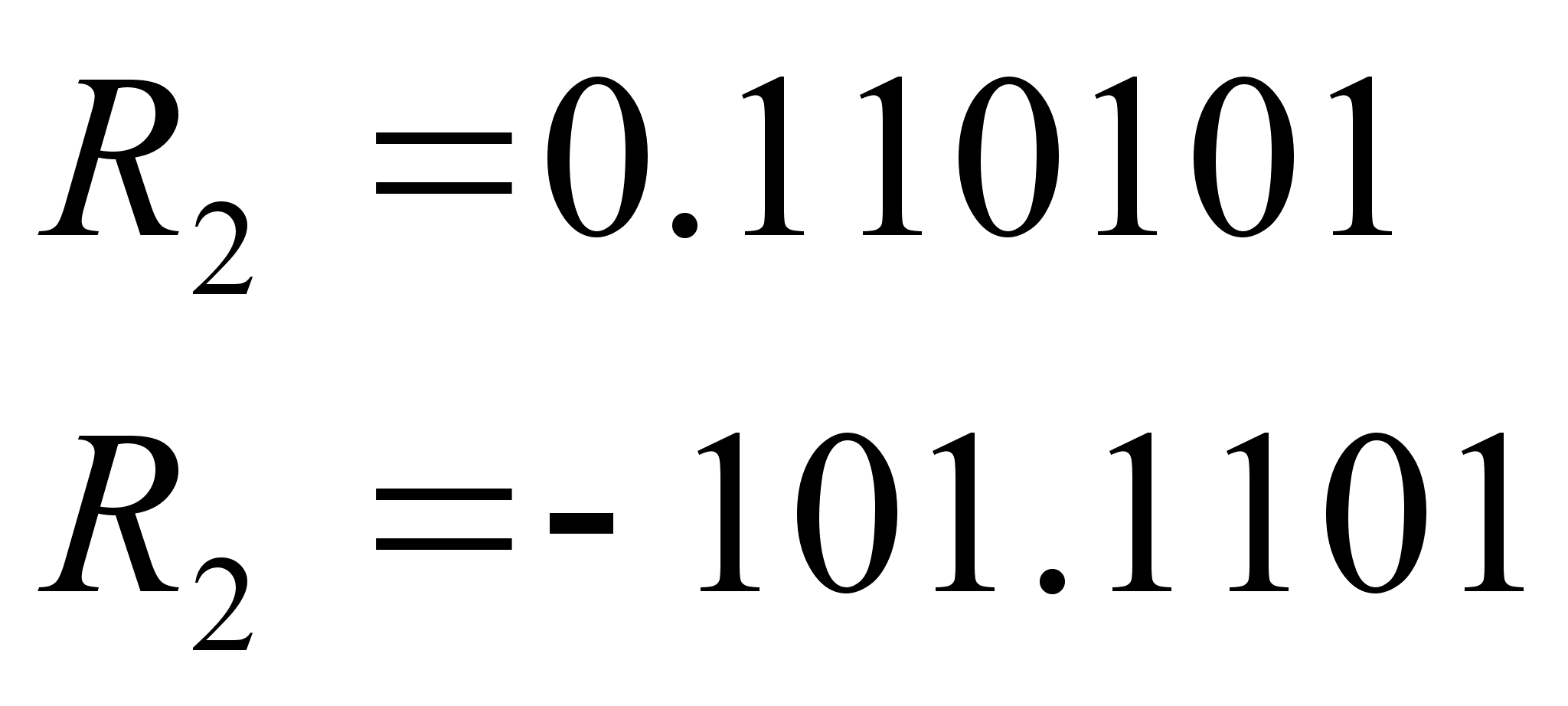
Из равенства
![]()
следует, что операцию вычитания y из x можно заменить операцией сложения S-y и х с последующим вычитанием из результата величины S.
Введем запись ![]() R
R ![]()
![]() = S+R
= S+R ![]()
Представление
чисел в соответствии
с ![]() называется
дополнительным
кодом числа
R.
называется
дополнительным
кодом числа
R.
Операцию вычитания можно заменить операцией сложения и на основе соотношения
![]() .
.
Код, определенный с помощью соотношения
![]() R
R
![]()
![]() =
= ![]()
![]()
называется обратным кодом числа R.
Отметим, что при S=2 для получения обратного кода отрицательного числа в знаковый разряд нужно записать единицу, а каждую цифру в записи числа заменить на ее дополнение до S-1, т. е. единицу заменить на нуль, а нуль на единицу.
Пример: Записать числа в обратном коде:
![]() =0,110101
=0,110101 ![]() =0 110101
=0 110101
![]() =
– 101,1101
=
– 101,1101 ![]() =1 0100010.
=1 0100010.
Пример: Записать числа в дополнительном коле:
![]() =0,110101
=0,110101
![]() =0 110101
=0 110101
![]() =
– 101,1101
=
– 101,1101
![]() =1 0100011
=1 0100011
Из приведенных примеров следует, что положительные числа в прямом, обратном и дополнительном кодах совпадают. В прямом и обратном коде нуль имеет два представления – «положительный» и «отрицательный» нуль. В дополнительном коде нуль имеет только одно, «положительное», представление.
Отметим, что при представлении с плавающей запятой отдельно кодируется мантисса и порядок числа. При этом возможно представление мантисс и порядков чисел в одном и том же или разных кодах. Например, порядок числа может быть представлен в прямом, а мантисса – в дополнительном кодах и т. п.
Таким образом, используя обратный и дополнительный коды, операцию алгебраического сложения можно свести к арифметическому сложению кодов чисел, которое распространяется и на разряды знаков, которые рассматриваются как разряды целой части числа.
Рассмотрим сначала использование обратного кода для алгебраического сложения n – разрядных двоичных чисел R и Q , когда оба они или одно из них отрицательно. Будем считать, что модуль их алгебраической суммы меньше единицы и единица переноса из разряда знака прибавляется к младшему разряду получившейся суммы.
Пусть, например,
![]() ( обозначим
( обозначим ![]() ) и
) и
![]() ( обозначим
( обозначим
![]() ).Считаем, - 1
).Считаем, - 1![]() 0.
Тогда в соответствии
с
0.
Тогда в соответствии
с ![]() можно записать
можно записать
![]() .
.
В
связи с тем,
что возникает
перенос из
знакового
разряда, одна
двойка пропадает
и добавляется
единица переноса
к младшему
разряду суммы
![]() :
:
![]() .
.
Таким образом, сложение с переносом единицы знакового разряда двух отрицательных чисел в обратном коде дает обратный код их алгебраической суммы.
Рассмотрим
алгебраическую
сумму чисел
![]() ( обозначим
( обозначим ![]() )
и
)
и ![]() .
Можем записать
.
Можем записать
![]() .
.
Если
![]() ,
то
,
то ![]() и возникает
перенос из
разряда знака.
В этом случае
имеем
и возникает
перенос из
разряда знака.
В этом случае
имеем
![]() .
.
Если
же ![]() ,то
,то
![]() и переноса не
возникает;
получаем
и переноса не
возникает;
получаем
![]() .
.
Мы получили, что сложение чисел с использованием обратных кодов с циклическим переносом приводит к получению алгебраической суммы в прямом коде, если сумма положительна, и в обратном коде, если сумма отрицательна.
Аналогично при использовании дополнительных кодов алгебраическое сложение их, включая разряды знаков, которые рассматриваются как разряды целых единиц, дает, если единица переноса из разряда отбрасывается, следующий результат: если алгебраическая сумма положительна, то результат получается в прямом коде, и в дополнительном коде, если она отрицательна.
Таким образом, применение обратного и дополнительного кодов дает возможность операцию алгебраического сложения свести к операции арифметического сложения. Однако нами рассмотрен случай, когда модуль полученной суммы меньше единицы. В общем случае при сложении двух чисел, модуль которых меньше единицы, модуль суммы может оказаться больше или равен единице ( так называемое переполнение разрядной сетки мантиссы ).
Для
обнаружения
такого переполнения,
учитывая, что
модуль суммы
двух таких
чисел меньше
двух, используют
один дополнительный
разряд. Код (
прямой, дополнительный,
обратный ), в
котором имеется
такой дополнительный
разряд, называется
модифицированным.
В модифицированных
кодах этот
разряд используется
для дублирования
знака числа,
т. е. знак «плюс»
обозначается
00, а «минус» - 11.
Правила переноса
из разрядов
знака остаются
прежними в
зависимости
от того, в каком
коде ( обратном
или дополнительном
) представлены
числа. На переполнение
же разрядной
сетки, т. е. что
модуль суммы
![]() ,
указывает
несовпадение
цифр в знаковых
разрядах. В
этом случае
комбинации
01 соответствует
положительное,
а 10 – отрицательное
число.
,
указывает
несовпадение
цифр в знаковых
разрядах. В
этом случае
комбинации
01 соответствует
положительное,
а 10 – отрицательное
число.
Пример:
Сложить ![]() и
и ![]()
Прямой
модифицированный
код ![]() 00
11011.
00
11011.
Обратный
модифицированный
код ![]() 11
11010.
11
11010.
+ 00 11011
11 11010
![]() 1
00 10101
1
00 10101
![]()
![]()
![]()
![]() 1
1
00 10110 = ![]() .
.
Пример:
Сложить ![]() и
и ![]()
![]() 11
01010
11
01010
![]() 11
00111.
11
00111.
+ 11 01010
11 00111
![]() (1) 10 10001
(1) 10 10001
![]() =10 10001
=10 10001
Переполнение разрядной сетки.
Таким образом, разрядные сетки в арифметическом устройстве имеют большее число разрядов, так как представления в модифицированном коде содержат второй ( дополнительный) знаковый разряд для мантиссы, а также второй знаковый разряд порядка ( для представления с плавающей запятой в отсутствии смещения порядка).
Итак, в общем случае сложение и вычитание в машинах с плавающей запятой состоит из следующих этапов:
1.Сравнение порядков чисел.
2.Выравнивание порядков чисел.
3.Перевод мантисс слагаемых в обратный или дополнительный модифицированные коды.
4.Сложение мантисс в прямом, обратном или дополнительном модифицированных кодах.
5.Исправление нормализации вправо или влево.
6.Перевод мантиссы результата в прямой код.
7.Выдача результата с учетом порядка.
Пример. Сложить два числа, представленные в форме с плавающей запятой.
R=0 011 1 111010001
Q=0 101 1 110101101,
где в первой позиции записи – знак порядка, в следующих трех – модуль порядка, затем следует знаковый разряд мантиссы и модуль мантиссы, т. е.
R=–0.111010001*![]()
Q=–0.110101101*![]()
а) Сравнение порядков. Из большего порядка вычитаем меньший:
![]() и
и ![]()
![]() .
.
б)
Выравнивание
порядков. Сдвигаем
мантиссу числа
R
на ![]() на (2) разрядов
вправо и присваиваем
ему порядок
на (2) разрядов
вправо и присваиваем
ему порядок
![]() :
:
R=0 101 1 001110100.
в) Переводим мантиссы в модифицированный обратный код:
![]() =11 110001011
=11 110001011
![]() =11 001010010
=11 001010010
г) Складываем мантиссы:
11 110001011
![]() 11 001010010
11 001010010
![]()
![]() 1 10 111011101
1 10 111011101
![]()
![]() 1
1
110 111011110
д) Несовпадение цифр в знаковом и контрольном разрядах указывает на нарушение нормализации влево. Сдвигаем мантиссу вправо на один разряд и соответственно увеличиваем порядок.
Получаем: мантисса 11 011101111; порядок 110.
е) Перевод мантиссы в прямой код:
1 100010000.
ж)
Результат R+Q=0
110 1 100010000, т. е. R+Q=![]() .
.
Список используемой литературы:
Ролич Ч. Н. – От 2 до 16, Минск, «Высшая школа», 1981г.
Математическая энциклопедия. М: “Советская энциклопедия” 1985г.
Шауман А. М. Основы машинной арифметики. Ленинград, Издательство Ленинградского университета. 1979г.
Калабеков Б. А. Цифровые устройства и микропроцессорные системы. М: “Горячая линия - Телеком” 2000г.
Ворощук А. Н. Основы ЦВМ и программирования. М:”Наука” 1978г.
Алексенко А. Г. Микросхемотехника. М: ”Радио и связь” 1990г.
1 Обратный код ![]() двоичного числа
двоичного числа ![]() называется также дополнением до 1, так как для каждого разряда числа
называется также дополнением до 1, так как для каждого разряда числа ![]() =1
=1
2 Дополнительный код ![]() числа
числа ![]() называется также дополнением числа до 2, так как для каждого разряда числа
называется также дополнением числа до 2, так как для каждого разряда числа ![]() ( число 2 в двоичной форме )
( число 2 в двоичной форме )
| ПРИМЕР | ||||||||||
 | ||||||||||
 | ||||||||||
Содержание
1 Происхождение и история развития систем счисления 1
1.1 Границы счета 1
1.2 Десятичная система счисления 2
1.3 Развитие понятия числа 2
1.4 Системы нумерации некоторых народов 3
2 Основные понятия и определения 8
3 Двоичная система счисления: основные сведения 10
3.1 История возникновения двоичной системы счисления 10
3.2 Основные понятия машинной арифметики 10
4 Взаимный перевод двоичных и десятичных чисел и элементарные
двоичные арифметические действия 11
4.1 Представление двоичных чисел и перевод их в десятичные 11
4.2 Преобразование десятичных чисел в двоичные 11
4.3 Арифметические действия над двоичными числами 13
5 Представление чисел в ЭВМ, кодирование 17
5.1 Представление чисел с фиксированной и плавающей запятой 17
5.2 Прямой, обратный и дополнительный коды.
Модифицированный код 19
5.3 Двоично-десятичное кодирование 21
6 Алгебраические действия над числами с плавающей и
фиксированной запятой 22
6.1 Сложение чисел с фиксированной запятой 22
6.2 Сложение чисел с плавающей запятой 22
6.3 Умножение чисел с фиксированной запятой 23
6.4 Умножение чисел с плавающей запятой 23
7 Другие системы счисления 23
Список использованной литературы
Похожие работы
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...
... представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа. Позиционные системы счисления В ...
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п





0 комментариев