Навигация
Двоичная система счисления: основные сведения
3 Двоичная система счисления: основные сведения
3.1 История возникновения двоичной системы счисления
Двоичная
система счисления,
т.е. система с
основанием ![]() ,
является
«минимальной»
системой, в
которой полностью
реализуется
принцип позиционности
в цифровой
форме записи
чисел. В двоичной
системе счисления
значение каждой
цифры «по месту»
при переходе
от младшего
разряда к старшему
увеличивается
вдвое.
,
является
«минимальной»
системой, в
которой полностью
реализуется
принцип позиционности
в цифровой
форме записи
чисел. В двоичной
системе счисления
значение каждой
цифры «по месту»
при переходе
от младшего
разряда к старшему
увеличивается
вдвое.
История развития двоичной системы счисления – одна из ярких страниц в истории арифметики. Официальное «рождение» двоичной арифметики связывают с именем Г. В. Лейбница, опубликовавшего статью, в которой были рассмотрены правила выполнения всех арифметических операций над двоичными числами. До начала тридцатых годов XX века двоичная система счисления оставалась вне поля зрения прикладной математики. Потребность в создании надежных и простых по конструкции счетных механических устройств и простота выполнения действий над двоичными числами привели к более глубокому и активному изучению особенностей двоичной системы как системы, пригодной для аппаратной реализации. Первые двоичные механические вычислительные машины были построены во Франции и Германии. Утверждение двоичной арифметики в качестве общепринятой основы при конструировании ЭВМ с программным управлением состоялось под несомненным влиянием работы А. Бекса, Х. Гольдстайна и Дж. Фон Неймана о проекте первой ЭВМ с хранимой в памяти программой, написанной в 1946 году. В этой работе наиболее аргументированно обоснованы причины отказа от десятичной арифметики и перехода к двоичной системе счисления как основе машинной арифметики.
3.2 Основные понятия машинной арифметики
В двоичной системе счисления используются только два символа, что хорошо согласуется с техническими характеристиками цифровых схем. Действительно очень удобно представлять отдельные составляющие информации с помощью двух состояний:
Отверстие есть или отсутствует (перфолента или перфокарта);
Материал намагничен или размагничен (магнитные ленты, диски);
Уровень сигнала большой или маленький.
Существуют специальные термины, широко используемые в вычислительной технике: бит, байт и слово.
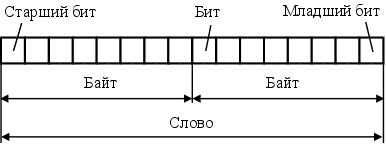
Битом называют один двоичный разряд. Крайний слева бит числа называют старшим разрядом (он имеет наибольший вес), крайний справа – младшим разрядом (он имеет наименьший вес).
Восьмибитовая единица носит название байта.
Многие типы ЭВМ и дискретных систем управления перерабатывают информацию порциями (словами) по 8, 16 или 32 бита (1, 2 и 4 байта). Двоичное слово, состоящее из двух байт, показано на рис. 3.1.
![]()
Рис. 3.1 Бит, байт и слово
4 Взаимный перевод двоичных и десятичных чисел и элементарные двоичные арифметические действия
4.1 Представление двоичных чисел и перевод их в десятичные
Совершенно очевидно, что двоичное число представляется последовательностью нулей и единиц – разрядов. Как и в любой позиционной системе, каждому разряду присвоен определенный вес – показатель степени основания системы. Веса первых 10 позиций представлены в таблице 4.1.
Таблица 4.1 Веса первых десяти позиций двоичной системы счисления
| Позиция | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Вес | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Образование |
|
|
|
|
|
|
|
|
|
|
В двоичной системе счисления даже сравнительно небольшие числа занимают много позиций.
Как и в десятичной системе, в двоичной системе счисления для отделения дробной части используется точка (двоичная точка). Каждая позиция слева от этой точки также имеет свой вес – вес разряда дробной части числа. Значение веса в этом случае равно основанию системы счисления (т.е. двойке), возведенному в отрицательную степень.
Получить десятичное число из двоичного чрезвычайно просто. Согласно формуле 2.3 для двоичной системы счисления получаем:
![]() (4.1)
(4.1)
Пример 4.1 иллюстрирует процесс получения десятичного числа из двоичного.
Пример
4.1 Перевод
двоичного числа ![]() в десятичное
в десятичное
![]()
4.2 Преобразование десятичных чисел в двоичные
Перевод из двоичной системы в десятичную несколько сложнее. Рассмотрим несколько алгоритмов.
4.2.1 Метод вычитания
Из десятичного
числа вычитаются
наибольшая
возможная
степень двойки,
в соответствующий
разряд двоичного
числа записывается
единица, если
разность меньше
следующей
степени двойки,
то далее записывается
нуль, а если
больше записывается
единица и опять
производится
вычитание, и
так до тех пор,
пока исходное
число не уменьшится
до нуля. В примере
4.2 рассматривается
перевод десятичного
числа ![]() в двоичное.
в двоичное.
Пример
4.2 Перевод
десятичного
числа ![]() в двоичное
методом вычитания
в двоичное
методом вычитания
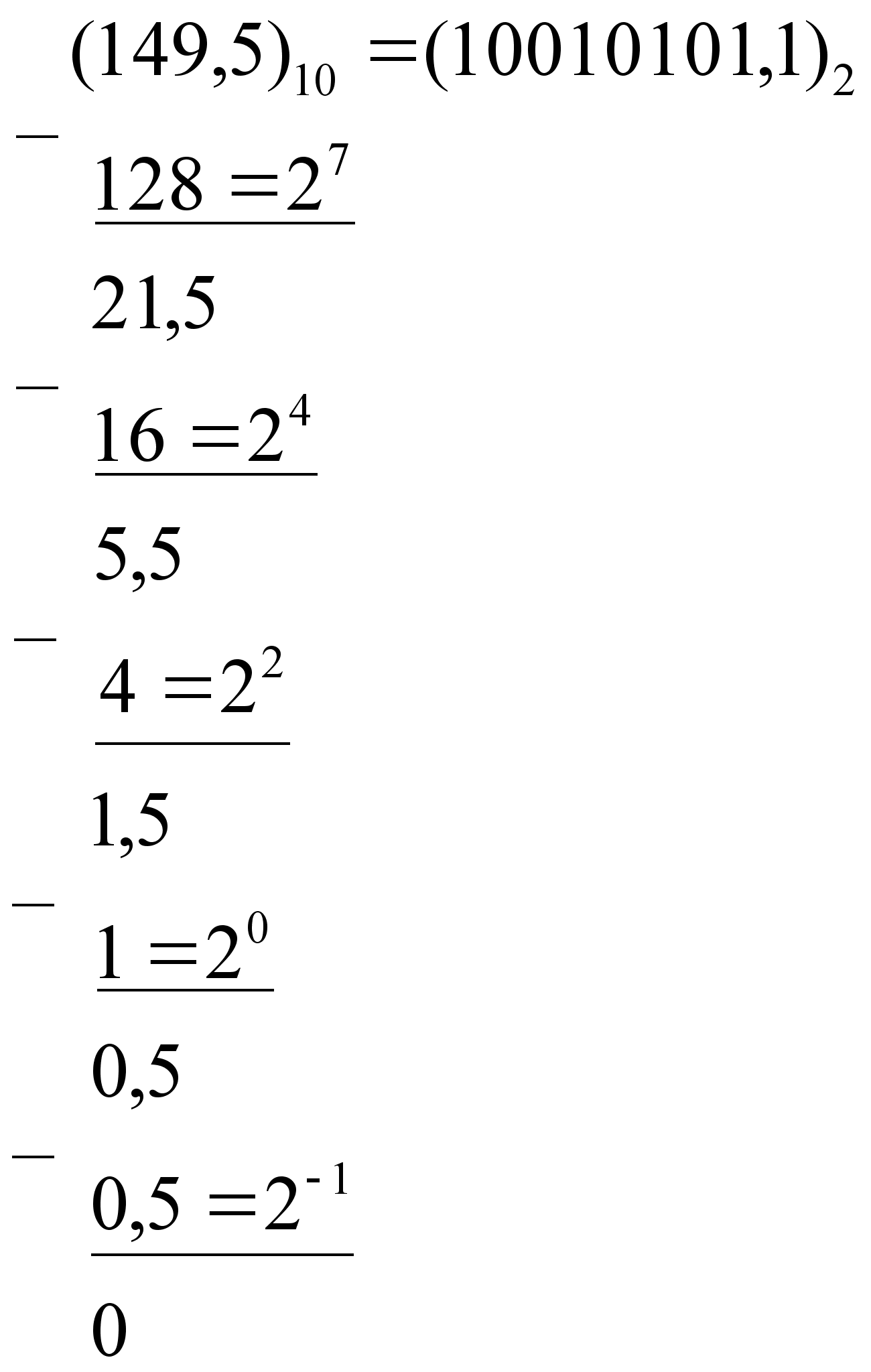
Похожие работы
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...
... представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа. Позиционные системы счисления В ...
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п





0 комментариев