Развитие понятия
числа
Славянская
нумерация
Римская
нумерация
Индийская
поместная
нумерация
Двоичная
система счисления:
основные сведения
Метод деления
Двоичное вычитание
Двоичное
деление
Числа с
плавающей
запятой
Двоично-десятичное
кодирование
Алгебраические действия над числами с плавающей и фиксированной
запятой
Другие системы
счисления
Прямой, обратный
и дополнительный
коды. Модифицированный
код. 20
Комбинация
знаковых цифр
мантиссы показывает,
что сумма
денормализована
влево (всегда
только на один
разряд)
Знак
произведения
1 + 0 = 1
Навигация
Метод деления
Системы счисления
95849
знаков
35
таблиц
321
изображение
4.2.2 Метод деления
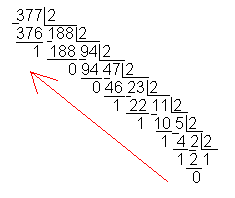
Другим методом является так называемый метод деления. Он применяется для преобразования целых чисел. Ниже приведен его алгоритм.
Разделим нацело десятичное число на двойку. Если есть остаток, запишем в младший разряд единицу, а если нет – нуль и снова разделим результат от первого деления. Повторим процедуру так до тех пор, пока окончательный результат не обнулиться.
Пример
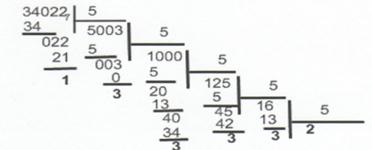
4.3 Перевод
десятичного
числа 
в двоичное
методом деления
|
| 2 | ||||||||
| 148 | –74 | 2 | |||||||
| 1 | 74 | –37 | 2 | ||||||
| 0 | 36 | –18 | 2 | ||||||
| 1 | 18 | –9 | 2 | ||||||
| 0 | 8 | –4 | 2 | ||||||
| 1 | 4 | –2 | 2 | ||||||
| 0 | 2 | –1 | 2 | ||||||
| 0 | 0 | 0 | |||||||
| 1 | | старший разряд | |||||||
| (10010101)2=(149)10 | ответ | ||||||||
4.2.3 Метод умножения
И, наконец, метод умножения. Метод применяется для преобразования десятичных дробей (чисел меньших единицы).
Число умножается на 2, если результат 1, то в старший разряд записывается единица, если нет, то нуль. Умножаем на 2 дробную часть результата и повторяем процедуру. И так далее до получения нужной степени точности или до обнуления результата.
Пример
4.4 Перевод
десятичного
числа 
в двоичное
методом умножения
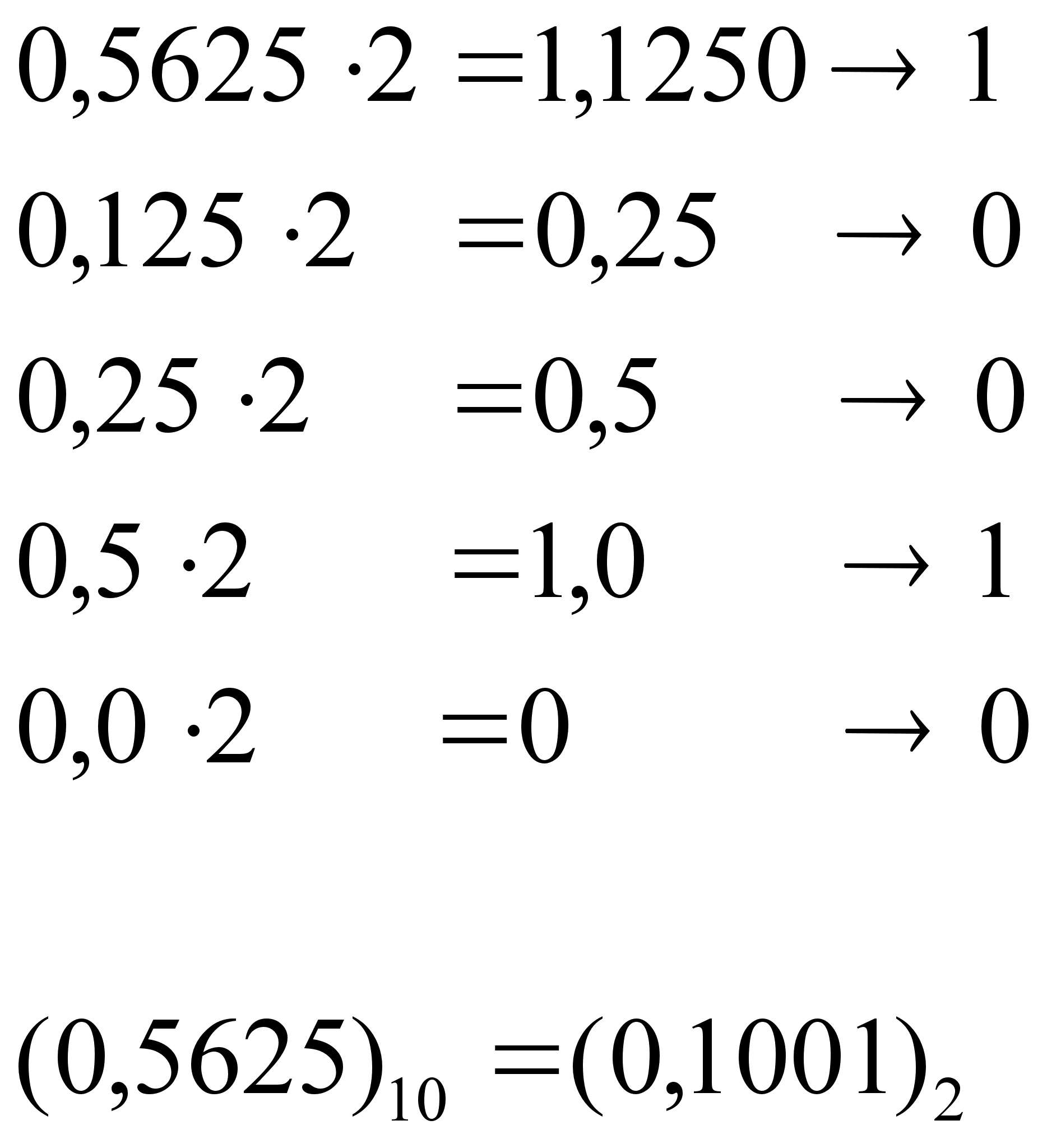
4.3 Арифметические действия над двоичными числами
Арифметика двоичной системы счисления основана на использовании таблиц сложения, вычитания и умножения. Эти таблицы чрезвычайно просты:
| Таблица сложения | ||||
| 0 | + | 0 | = | 0 |
| 0 | + | 1 | = | 1 |
| 1 | + | 0 | = | 1 |
| 1 | + | 1 | = | 10 |
| Таблица умножения | ||||
| 0 | * | 0 | = | 0 |
| 0 | * | 1 | = | 0 |
| 1 | * | 0 | = | 0 |
| 1 | * | 1 | = | 1 |
| Таблица вычитания | ||||
| 0 | – | 0 | = | 0 |
| 1 | – | 0 | = | 1 |
| 1 | – | 1 | = | 1 |
| 10 | – | 1 | = | 1 |
4.3.1 Двоичное сложение
Двоичное сложение выполняется по тем же правилам, что и десятичное, с той лишь разницей, что перенос в следующий разряд производиться после того, как сумма достигнет не десяти, а двух.
Пример
4.5 Сложение
двоичных чисел 
и 
| + | 101101 | |
| 111110 | ||
| 010011 | – поразрядная сумма без учета переносов |
| + | 1011000 | – переносы |
| 0010011 | ||
| 1001011 | – поразрядная сумма без учета повторных переносов |
| + | 0100000 | – повторные переносы |
| 1001011 | ||
| 1101011 | – окончательный результат |
Легко произвести проверку:
,
,
,
.
Пример
4.6 Сложение
двоичных чисел 
и 
| + | 110, | 1011 | |
| 10111, | 10101 | ||
| 10001, | 00011 | – поразрядная сумма без учета переносов | |
| + | 11 1, | 1 | – переносы | |
| 10001, | 00011 | |||
| 11100, | 01011 | – поразрядная сумма без учета повторных переносов | ||
| + | 1 , | – повторные переносы | ||
| 11100, | 01011 | |||
| 11110, | 01011 | – окончательный результат | ||
Сложение нескольких чисел вызывает некоторые трудности, так как в результате поразрядного сложения могут получится переносы, превышающие единицу.
Похожие работы
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...
... представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа. Позиционные системы счисления В ...
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п
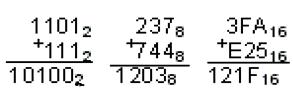
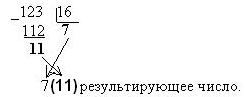
0 комментариев