Символика Виета и развитие алгебры

2.2 Символика Виета и развитие алгебры.

Виет считается одним из основоположников алгебры. Но его интерес к алгебре первоначально связан с возможными приложениями к тригонометрии и геометрии. А задачи тригонометрии и геометрии, в свою очередь, приводили Виета к важным алгебраическим обобщениям. Так было, например, с решением уравнений третьей степени в неприводимом случае и с исследованием некоторых классов разрешимых алгебраических уравнений высших степеней.

Свою алгебру Виет ценил очень высоко. Он не пользовался словом «алгебра», эту науку он зазывал «искусством анализа». Виет различал видовую логистику и числовую логистику. Термин «логистика» означает совокупность арифметических приемов вычислений, «вид» имел смысл символа.

Видовая логистика Виета после внесенных им в символику усовершенствований представляла собой буквенное исчисление. Ее объектами служат геометрические и псевдогеометрические образы, связанные между собой различными соотношениями. Виет был последователем древних: он оперировал такими величинами, как сторона, квадрат, куб, квадратоквадрат, квадратокуб , и т. д., образующими своеобразную лестницу скаляров. Действия над скалярами у Виета, как и у древних геометров, подчинены «закону однородности»: составленные из неизвестных и известных величин уравнения должны быть однородными относительно всех их вместе взятых. Умножению чисел у Виета соответствует образование нового скаляра, размерность которого равна сумме размерностей множителей. Операция, соответствующая делению чисел, дает новую величину, размерность которой равна разности размерностей.

Виет разработал символику, в которой наравне с обозначением неизвестных впервые появились знаки для произвольных величин, называемых в настоящее время параметрами. Для обозначения скаляров он предложил пользоваться прописными буквами: «искомые величины будут обозначены буквой А или другой гласной Е, I, О, U, Y, а данные – буквами B, D, G или другими согласными»

Слово «коэффициент» введено Виетом. Рассматривая выражение

(А + В)² + D(A + В),

он назвал величину D, участвующую с А + В в образовании площади, longitude ciefficiens, т. е. содействующей длиной.

Из знаков Виет употреблял +, — и дробную черту. Современные скобки у него заменяла общая черта на всем выражением.

Символика Виета страдала недостатками, в некоторых отношениях она была менее совершенна, чем у его предшественников и современников. Виет для записи действий употреблял слова: in у него означало умножение, aequatur заменяло знак равенства. Словами же выражались степени различных величин. Для трех низших степеней он взял названия из геометрии, например, А³ называл A cubus. Высшим степеням он давал геометрические наименования, происходящие от низших: А⁹, например,— A cubo-cubo-cubus. Известная величина В представлялась как величина девятой степени записью solido-solido-solidum. Если сторона (latus) умножается на неизвестную величину, то она называется содействующей) (coefficiens) при образовании площади.

Уравнение А³ + 3ВА = D Виет записывал так: А cubus + В planum in 43 aequatur D solido, а уравнение ВАⁿ –А^m+n = Z так:

В parabola in А gradum — А potestate aequatur Z homogenae (В, умноженное на градус А, минус А в степени равняется однородной Z),

Обозначения в числовой логистике выглядели проще:

N – первая степень, Q – квадрат, С – куб и т. д. Уравнение x³ - 3x = 1 записывалось в виде 1С – 3N aequatur 1»

Неудобства символики Виета связаны и с требованием однородности. Как и древние греки, Виет считал, что сторону можно складывать только со стороной, квадрат – с квадратом, куб – с кубом и т. д. В связи с этим возникал законный вопрос: имеют ли право на существование уравнения выше третьей степени, поскольку в пространственном мире четвертая, пятая и т. д. степени аналогов не имеют.

Для придания уравнению однородности Виет после входящих в него параметров писал planum (плоскость), solidum (тело) и т. д. Вот как выглядит в записи Виета уравнение х³ + ЗВ²х = 2z³: A cubus + В plano 3 in A aequari Z solido 2.

Правило Тартальи для решения уравнения третьей степени у Виета имело вид:

.

Символики Виета придерживался впоследствии П. Ферма. От «тирании» однородности просто и остроумно сумел освободиться Декарт (об этом будет сказано дальше).

Может показаться, что Виет ввел в символику алгебры совсем немного. Буквами для обозначения отрезков пользовались еще Евклид и Архимед, их успешно применяли Леонардо Пизанский, Иордан Неморарий, Николай Орем, Лука Пачоли, Кардано, Бомбелли и многие другие математики. Но сделал существенный шаг вперед Виет. Его символика позволила не только решать конкретные задачи, но и находить общие закономерности и полностью обосновывать их. Это, в свою очередь, способствовало выделению алгебры в самостоятельную ветвь математики, не зависящую от геометрии. «Это нововведение (обозначение буквами данных и искомых) и особенно применение буквенных коэффициентов положило начало коренному перелому в развитии алгебры: только теперь стало возможным алгебраическое исчисление как система формул, как оперативный алгоритм».

Сказанное, легко подтвердить примерами. Пусть х₁, x₂ – корни квадратного уравнения. Перемножим разности x – x₁ и х – х₂: (x – x₁)(х – х₂)=х² – (х₁ + х₂)х + х₁х₂.

Обозначим (x – x₁)(х – х₂) = х² + px + q, сравнивая с предыдущим, получим p = – (х₁ + х₂), q = x₁x₂.

Выполним то же самое для кубического уравнения:

(x – x₁)(х – х₂)(x – x₃)=x³ – (х₁ + х₂ + x₃)x² + (x₁x₂ + x₁x₃ + x₂x₃)x – x₁x₂x₃.

Сравним результат с выражением (x – x₁)(х – х₂)(x – x₃) = x³ + a₁x² + a₂x + a₃.

Это дает a₁ = – (x₁ + x₂ + x₃)

 a₂ = x₁x₂ + x₁x₃ + x₂x₃

 a₃= – x₁x₂x₃.

Такой результат для квадратного уравнения был известен Кардано (в случае положительных корней – еще и раньше); Кардано отметил свойство корней кубического уравнения относительно коэффициента при х². Но никакого обоснования в общем виде дать он не мог; это сделал Виет для уравнений до пятой степени включительно.

Преимущества символики предоставили Виету возможность не только получить новые результаты, но и более полно и обоснованно изложить все известное ранее. И если предшественники Виета высказывали некоторые правила, рецептуры для решений конкретных задач и иллюстрировали их примерами, то Виет дал полное изложение вопросов, связанных с решением уравнений первых четырех степеней.

Рассмотрим ход рассуждений Виета при решении кубического уравнения.

Возьмем уравнение x³ + 3ax = 2b. Положим a = t² + xt.

Найдем отсюда

х =  и подставим в исходное уравнение. Получим  + 3a = 2b, откуда для определения t наводим квадратное уравнение относительно t³: (t³)² + 2bt³ – а³ == 0.

Отсюда определится t, а затем и х. Заметим еще, что подстановка а = t² + xt приводит исходное уравнение к виду

(х + t)³ – t³ = 2b,

которое вместе с уравнением (х + t)t = a, (х + t)³t³ = a³ дало бы возможность применить метод Тартальи и дель Ферро. Но Виет таким путем не пошел.

Рассмотрим теперь пример. Найдем методом Виета действительный корень уравнения

х³ + 24x=56.

Здесь а=8, b=28. Запишем уравнение относительно t: (t³)² + 56t³ - 8³ - 0.

Решим его:

t³= –28 = – 2836 t₁ = = 2 t₂ = = –4.

Найдем теперь х:

x₁ =  = –2 , x₂ =  = 2 = x₁.

При изложении метода Феррари для решения уравнения четвертой степени Виет провел аналитически выкладки, указанные выше, и получил уравнение, содержащее основную неизвестную А и вспомогательную Е (х и t у Феррари).

 Виет, верный последователь древних, оперировал только рациональными положительными числами, которые он обозначал буквами. Если в результате подстановки в уравнение значений параметров неизвестное оказывалось иррациональным, он давал этому случаю особое обоснование.

В качестве примера такого обоснования приведем «геометрическое» решение кубического уравнения по способу дель Ферро – Тартальи.

В записи Виета уравнение имело вид A³ + 3BA = D.

Известное решение: А является разностью «сторон» которые образуют площадь В и разность кубов которых равна D. Если обозначить «стороны» буквами u и v, то uv = B, u³ – u³ =D, A= u –v.

Виет придавал решению «геометрическое» толкование; он вместо D solidum записывал произведение В planum на D, т. е. получал уравнение A³ + 3ВA= BD.

Затем он определял четыре величины, образующие «геометрический ряд», так, чтобы прямоугольник, построенный на средних или на крайних, по площади равнялся В, а разность крайних была D. Тогда A будет разностью средних.

Поясним сказанное. Обозначим эти четыре величины через z, u, v и t. Тогда можно записать

z:u = u:v = v:t, zt = uv = B, z – t = D, A = u – v.

Если в решении Тартальи D заменить на BD, то оба решения совпадут.

Способ Виета означает замену кубического корня двумя средними геометрическими, что полностью соответствует духу древних греков.

Из получившихся пропорций найдем

u³ = z²t, v³ = zt u³ – v³ = zt(z – t) = BD

Виет особо рассматривал трехчленные уравнения различных степеней и в первую очередь интересовался количеством их корней, имея в виду только положительные корни. Отрицательные корни он определял как корни уравнения, в котором неизвестное х заменено на –у. Виет , получал трехчленные уравнения из квадратных; он поступал так, чтобы число положительных корней оставалось прежним. При этом он пользовался подстановкой х = ky^m или специальными приемами.

Один из приемов Виета выглядит так. Пусть дано уравнение

x² + ах = b, а, b>0.

Для получения уравнения четвертой степени возведем левую и правую части уравнения в квадрат:

(х² + ах - b)³ = x⁴ + a²x² + b² + 2ax³ – 2bx² – 2abx = 0

Полученное уравнение можно переписать:

x⁴ + 2ах³ + 2а²x² – а²x²+ b² – 2bх² – 2abx = 0.

Исключим 2ах³ + 2a²x², воспользовавшись тем, что b = х² + ax:

2ах(х² + аx) = b2аx, 2ах³ + 2a²x = 2abx.

Тогда x⁴ + 2abx – а²x² + b² – 2bx² – 2abx = 0, x⁴ – a²x² + b² – 2bx² = 0.

Теперь осталось исключить x²; из исходного уравнения найдем: x² = b – ax и подставим в последнее:

 x⁴ – (a² + 2b)x² + b² = 0, x⁴ – (a² + 2b)(b – ax) + b² = 0, x⁴ + (2ab + a³)x = b² + a²b

Полученное уравнение четвертой степени имеет те и только те положительные корни, которые были у исходного квадратного.

Для нахождения трехчленного уравнения третьей степени Виет в качестве исходного брал уравнение

ax – x² = ab

и умножал его левую и правую части на х + b; это при водило к уравнению

(а – b)х² – х³ = ab²

с теми же положительными корнями, которые были у квадратного.

И еще один частный вопрос рассмотрел Виет. В уравнении

ах^m – x^m+n = b

имеющем по условию два корня, он определил коэффициенты, при которых корни уравнения имели бы заданные значения.

Пусть эти корни у и z. Тогда

a =, b =

Ту же задачу он решил относительно уравнения

x^m+n + ax^m = b, где m + n – число четное, m – нечетное.

Чрезвычайно важно то, что Виет распространил известные ранее частные преобразования на все алгебраические уравнения. Подстановку х = у + k, применявшуюся Кардано для исключения из кубического уравнения члена второй степени, он применил к уравнениям любой степени. Также известную Кардано обратную подстановку х = k/y Виет употреблял, чтобы освободиться в некоторых случаях от отрицательных коэффициентов и иррациональностей. Например, уравнение х⁴ – 8х = подстановкой х =  он преобразовал к виду y⁴ + 8у³ = 80. Подстановкой х = y Виет преобразовывал уравнение n-й степени так, что коэффициент при члене (n -1)-й степени (a) становился равным b, в то время как старший коэффициент оставался равным единице. Подстановку х = ky он применял, чтобы избавиться от дробных коэффициентов.

Особый интерес представляет исследование Виета по составлению уравнений из линейных множителей и по установлению связей между корнями уравнения и его коэффициентами. Первоначальные сведения и по тому, и по другому вопросу были у Кардано.

Кардано в ту пору, когда еще не знал метода дель Ферро и Тартальи, решал некоторые уравнения третьей степени разложением на множители. В уравнении

2х³ + 4x² + 25 = l6x + 55

с этой целью он прибавлял к обеим частям 2x² + 10x + 5. Затем преобразовывал его к виду (2х + 6)(х² + 5) = (х + 10)(2х + 6), сокращал на 2х + 6 и получал квадратное уравнение.

Кардано же при нахождении положительного корня уравнения х³ + b = ах складывал его почленно с уравнением у³ = ay + b, получал из них квадратное уравнение делением на х минус известный отрицательный корень х – (–у). Такое преобразование позволило Кардано установить, что коэффициент при члене второй степени в правой части кубического уравнения равен сумме его корней. Это был первый шаг к установлению зависимости между корнями и коэффициентами алгебраического уравнения.

Виет составил полные уравнения с заданными положительными корнями вплоть до пятой степени и показал, как образуются коэффициенты при x^n-1, x^n-2, x^n-3, ... Он установил, что эти коэффициенты при условии, что старший коэффициент равен 1 или –1 (свободный член в правой части должен был стоять со знаком +), представляют собой взятые с чередующимися знаками суммы: самих корней, парных произведений их, произведений корней, взятых по три, и т. д. Работа, в которой Виет подробно рассмотрел это утверждение, до нас не дошла. Неизвестно, как он поступал в том случае, когда уравнение имеет и отрицательные корни. Но, скорее всего, это не представляло для Виета особых трудностей: достаточно было сделать в уравнении замену х = –у и можно оперировать с положительными корнями нового уравнения. Такие примеры в его работах встречались. Если уравнение х³ + q = рх имеет два положительных корня х₁ и х₂, то уравнение y³ = ру + q – один положительный корень у₁ = –х₃ причем у₁ = х₁ + х₂ (это знал Кардано), x₁² + x₂² + x₁x₂ = p, x₁x₂(x₁ + x₂) = q.

Как видим, в исследованиях Виета встречались начала теории симметрических функций и разложения многочленов на линейные множители, что вскоре привело к открытию основной теоремы алгебры о числе корней уравнения произвольной степени. Эти исследования Виета продолжили математики следующего поколения Т. Гарриот (1560— 1621), А.Жирар (1595-1632), Р. Декарт (1596-1650).

Похожие работы

Символика и значения числовых компонентов в английских фразеологических единицах

Скачать

128557

5

0

... neat as ninepence - чистенький, аккуратный; с иголочки; a twice-told tale - старая история, что-либо часто повторяемое и потому хорошо известное. 2. Значения числовых компонентов в английских фразеологических единицах Имена числительные, являясь абстрактным показателем количества однородных предметов, обозначением их счета, замкнуты в своеобразную категорию количественных слов, которые лишены ...

Теоретические подходы к феномену "математическое мышление"

Скачать

31592

0

0

... схемы; 9) способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики, как геометрия, Сторонники шестого подхода считают, что математическое мышление является мышлением теоретическим и имеет такую же последовательность становления от эмпирического к аналитическому, к планирующему, рефлексирующему (Р. Атаханов, В.В. Давыдов, Ле Тхи Кхань Кхо, ...

Моделирование в развитии математических представлений дошкольников

Скачать

57247

0

0

... с активными познавательными обследовательскими действиями, со способностью к замещению предметов посредством условных знаков, символов».(7,с.126) 3. Моделирование в развитии математических представлений дошкольников Поиск эффективных средств познавательного развития детей, выявление условий становления познавательной де­ятельности в дошкольном детстве является темой научных работ многих ...

Математическое моделирование в экономике

Скачать

16669

0

6

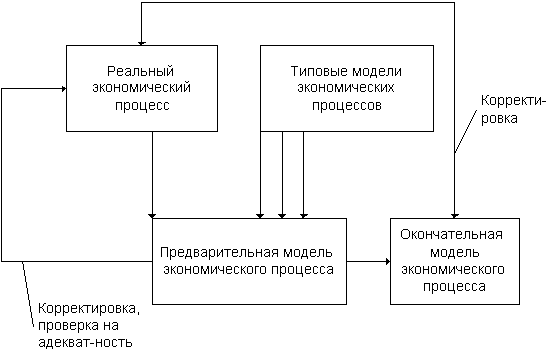
... заданное его качество, определение оптимальных (с точки зрения принятого критерия) норм дежурного обслуживания, надобность в котором возникает непланомерно, нерегулярно. С использованием метода математического моделирования можно определить, например, оптимальное количество автоматически действующих машин, которое может обслуживаться одним рабочим или бригадой рабочих и т.п. Типичным примером ...